物理引导的SSA-BiGRU 输电线路覆冰厚度预测模型
2022-03-04李英娜
于 童,李英娜
(昆明理工大学 信息工程与自动化学院,云南 昆明 650500)
0 引言
输电线路覆冰是一种严重的自然灾害。覆冰会导致线路舞动[1,2]、导线断裂,严重危害电网的安全运行。
国内外学者在线路覆冰预测模型方面的研究大致分为3 种:物理机理模型[3]、统计计算模型[4-8]和智能计算模型[9-15]的研究。覆冰机理模型有Goodwin 模型、Makkonen 模型[3]等。统计计算模型研究方面:文献[4]提出直线塔受力分析覆冰计算模型。文献[5,6]利用倾角、拉力等检测数据计算覆冰厚度实现覆冰厚度预测。文献[7]利用模糊理论建立了基于气象信息的线路覆冰厚度预测模型,通过多变量时间序列计算结冰厚度。文献[8]提出了改进的冻结系数计算方法,再结合微气象数据进行了覆冰厚度计算。
近几年,对于线路覆冰预测研究趋向于智能算法模型。文献[9,10]基于BP(back propagation)神经网络和支持向量机(support vector machines,SVM)等算法,提出了基于思维进化算法优化的覆冰厚度智能预测方法。文献[11]分析了微气象参数之间的相关性,并结合灰色关联分析结果,建立了基于环境温度和风速的多变量灰色覆冰预测模型。文献[12]将覆冰期分为几个阶段,再使用蝙蝠算法(bat algorithm,BA)优化后的输入权重和偏置阈值建立极限学习机(extreme learning machines,ELM)预测覆冰厚度。文献[13]使用扩展记忆粒子群(particle swarm optimization with extended memory,PSOEM)优化最小二乘支持向量机(least squares support vector machines,LS-SVM)模型超参数构建预测模型。文献[14]使用主成分分析(principal component analysis,PCA)提取特征,采用量子进化烟花算法(quantum-behaved fireworks algorithm,QFA)对LSSVM 超参数进行寻优,并构建覆冰预测模型。文献[15]采用变分模态分解(variational mode decomposition,VMD)对覆冰序列分解,然后分别使用改进灰狼算法(improved gray wolf algorithm,IGWO)优化LSSVM 模型预测各分量,最后再累加得到覆冰预测值。文献[16]采用自适应变异粒子群算法(adaptive mutation particle swarm optimization algorithm,AMPSO)优化BP 神经网络的权值阈值,进而构建覆冰预测模型。
以上智能算法模型均采用了数据驱动的思想,但并未将覆冰的客观规律与算法相结合。因此,本文采用物理引导(physics-guide,PG)神经网络[17,18]的思想,将覆冰现象中的物理规律与麻雀搜索算法(sparrow search algorithm,SSA)优化的双向门控循环(bi-directional gated recurrent unit,BiGRU)神经网络结合,使用覆冰监测系统采集到的输电线路综合荷载数据对模型训练过程进行引导,旨在提升输电线路覆冰厚度预测模型的准确性,提高模型的真实性。
1 基于物理引导的覆冰模型修正
对于输电线路,一般采用微气象因素作为特征对其进行覆冰预测。输电塔体系上的监测系统可收集到一些物理参量数据,如综合荷载、风偏角等。这些实时监测数据虽然不能在深度学习模型中用作预测覆冰厚度的特征参数,但其与覆冰存在很大的关联;因此,本文尝试分析综合悬挂荷载、覆冰厚度以及一些其他参数,然后根据所得的相应关系挖掘其中的客观物理规律;再将规律与预测模型结合,使其在后续使用的BiGRU 模型训练过程中起到修正作用,使模型与覆冰现象的形成过程更加契合,避免预测结果出现违背物理规律的情况。
1.1 输电塔线风冰荷载静力学计算模型
首先对输电塔线进行受力分析。在静力学的范畴内,输电线在覆冰状态下受到3 种荷载,即来自导线的自重、覆冰重量引起的纵向荷载、风压引起的横向荷载[5]。导线的受力分析如图1所示。
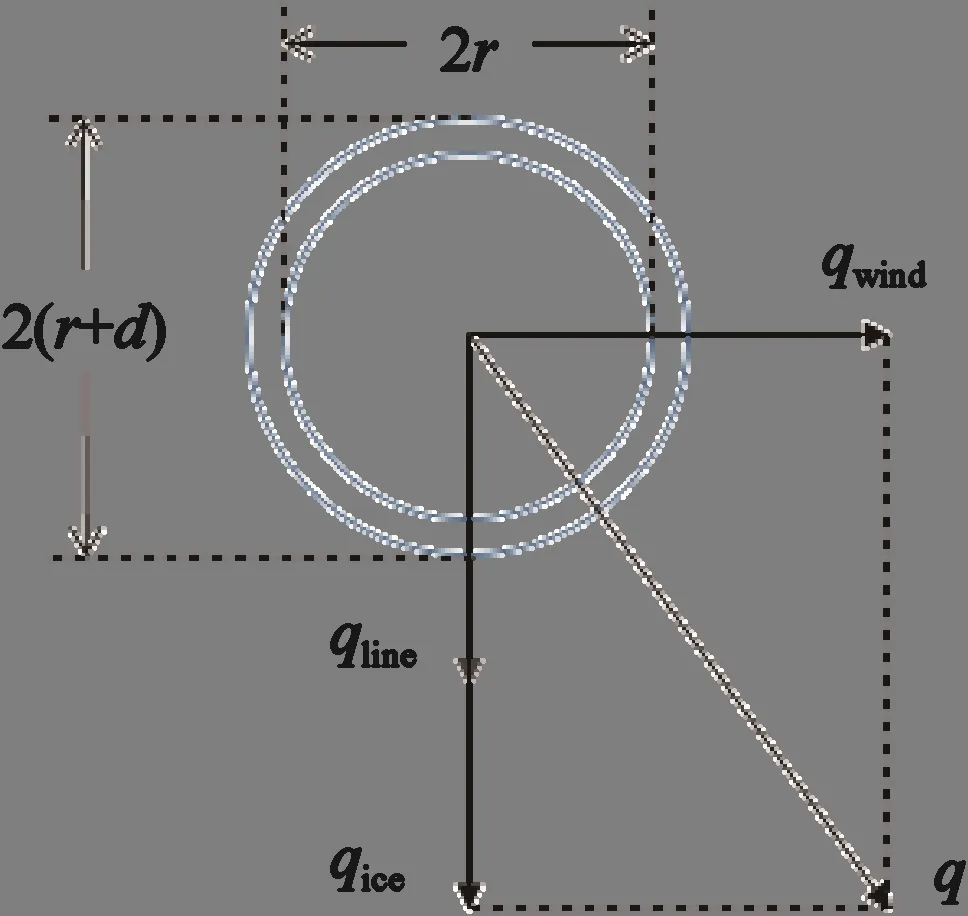
图1 覆冰输电线路受力分析Fig.1 Force analysis of ice-coated transmission lines
图中:r为导线半径,mm;d为覆冰厚度,mm;qice、qline、qwind和q分别为单位长度导线所受的冰荷载、自重荷载、风荷载以及综合荷载,N/m。综合荷载的计算有2 种方法:
(1)分别计算出垂直荷载和水平荷载,再计算合力q,如式(1)所示。

(2)风偏角根据垂直荷载直接推算得出,如式(2)[6]所示。

计算风荷载需要引入风速不均匀系数等模糊参数,故而会出现计算的误差;而风偏角可以直接由传感器所采集的数据获得,因此:选用第2 种方法计算。
风偏平面内,导线综合荷载如图2 所示。
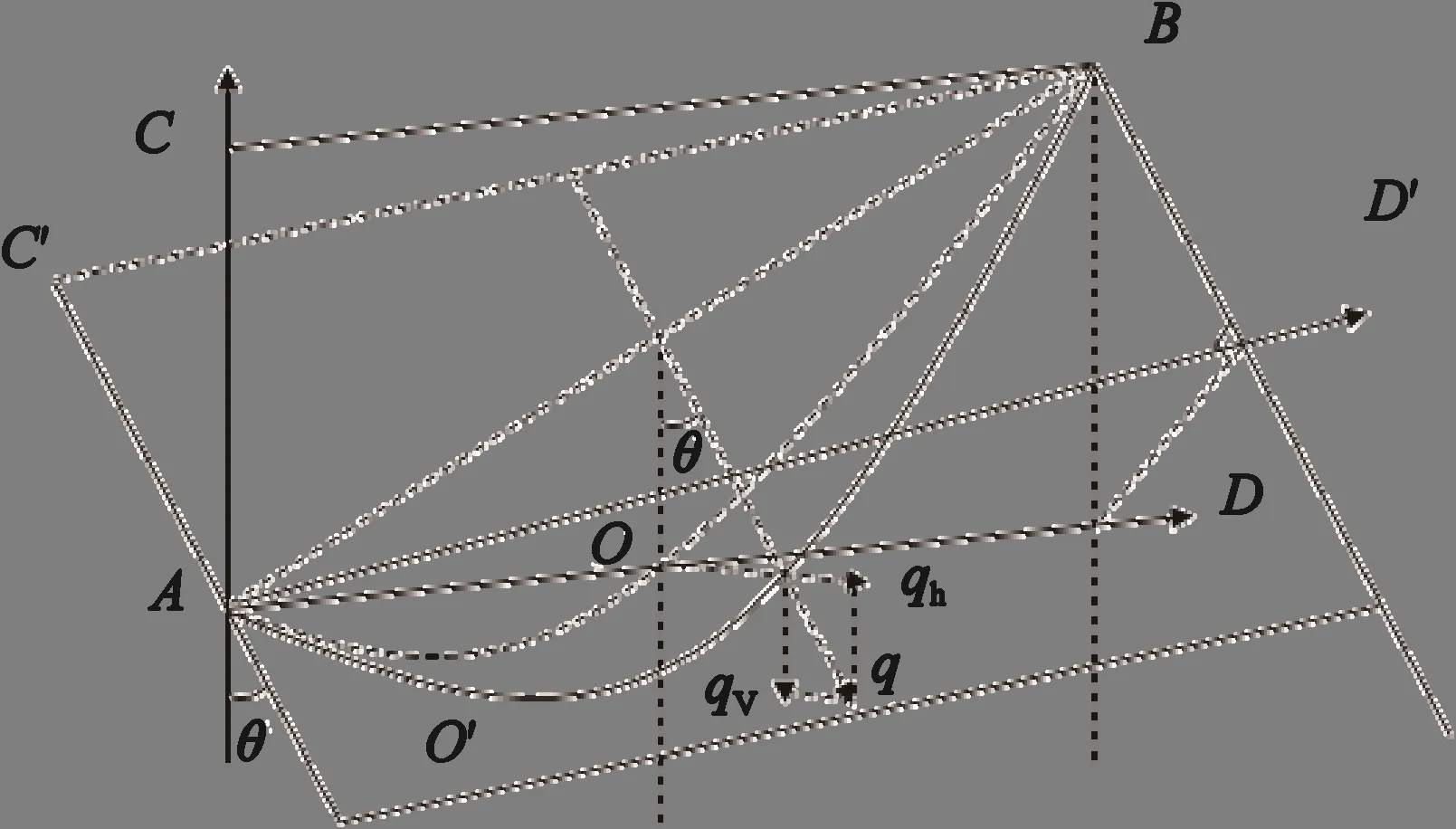
图2 风偏平面内覆冰输电导线综合荷载Fig.2 Comprehensive load of ice-coated transmission lines in the wind deflection plane
图中:ACBD为无风作用平面;AC′BD′为风偏平面;qh、qv分别为单位长度导线所受水平荷载、垂直荷载;θ为风偏角。
输电塔体系模型构建条件假设:输电线上所受的综合荷载引起的应力在导线能承受的最大应力范围内;导线长度不变。那么导线垂直荷载计算模型如下:
(1)导线自重的荷载
导线单位自重荷载可以通过式(13)计算。

式中:G为单位长度导线质量,kg/km。
(2)覆冰引起的荷载
等值覆冰导线的单位冰荷载为:

式中:V为单位长度导线覆冰体积,cm3;ρice为等值覆冰密度,g/cm3。
则覆冰导线在垂直方向上的荷载包含导线自重引起的自重荷载以及冰荷载,即:
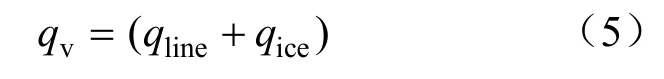
总导线综合荷载Q为:

式中:S为导线长度。实验中,已知单段导线自重1 890 N。
通过式(2)(6)得到综合荷载如式(7)所示。
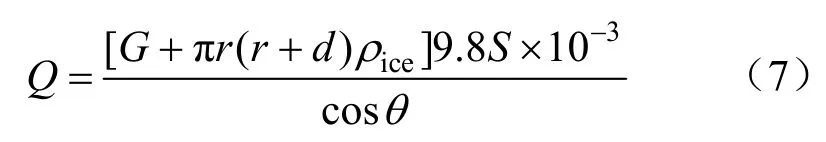
根据式(7),可总结出覆冰厚度和风偏角分别增大时,覆冰厚度也相应增大的规律。
由图3 可以看出,综合荷载、覆冰厚度和风偏角三者之间的关系。后续实验中所用数据并未达到图中各轴的最大值。

图3 综合荷载、覆冰厚度、风偏角关系图Fig.3 Relation diagram of comprehensive load,icing thickness and wind deflection angle
1.2 物理引导的修正方法
根据上述规律,使用传感器采集的综合荷载数据对模型的训练过程进行修正,修正以自定义损失函数的方法实现。将模型当前时刻对覆冰的预测值、风偏角数据、综合荷载数据分别与上一时刻进行比较。风偏角角度增大时,预测覆冰厚度增大,但综合荷载数据减小;在风偏角数减小时,预测覆冰厚度减小,但综合荷载数据增大。以上2种情况都违反了综合荷载的客观变化规律。因此,在这2 种情况下,反馈给模型一个正的损失函数值;预测结果不违反物理规律或由于不能保证控制变量原则而无法判断是否违反的情况下,则返回0。以此修正模型的训练过程,使其模型更加贴近覆冰现象的真实规律。
设模型训练过程中的损失函数f为[17-18]:

式中:λ是一个系数,用于表示经验损失函数LOS S(,y)和 PHYloss(,Q,θ)的尺度差异。

经验损失函数使用均方误差:
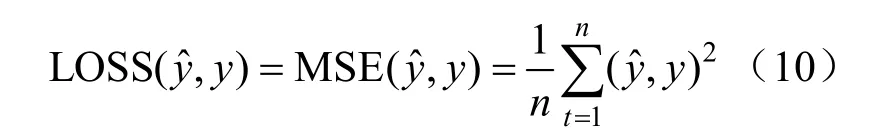
在模型的训练过程中,为判断理论上综合荷载的变化趋势和真实的综合荷载变化趋势是否一致,需分别比较当前时刻预测覆冰厚度、风偏角与实际综合荷载本身与上一时刻的差值,分别记为Δd(t)、Δθ(t)、ΔQ。
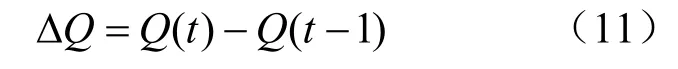
当Δθ(t)=|θ(t)|–|θ(t–1)|≤0 且Δd(t)=d(t)–d(t–1)≤0时,此时 Δ≤0,若ΔQ(t)≥0,记为情况①。当Δθ(t)=|θ(t)|–|θ(t–1)|≥0 且Δd(t)=d(t)–d(t–1)≥0 时,此时 Δ≥0,若ΔQ(t)≤0,记为情况②,此时PHYloss(t)返回一个正值。与情况①、情况②均为物理不一致的情况,记为情况③,PHYloss(t)返回0。
使用RULE 函数实现分段函数功能,则基于物理的损失函数见式(12)(13)。

2 预测模型构建
2.1 麻雀搜索算法
麻雀搜索算法是一种仿生优化算法,模仿麻雀群体觅食行为和反捕食行为[19-20]。麻雀觅食的过程即为在某范围内寻优的过程。使用SSA 算法数学模型,麻雀群体表示为:

式中:n为个体数;d为变量的维度。
生产者可以在整个搜索空间内自由移动并寻找食物,其位置更新见式(15)。

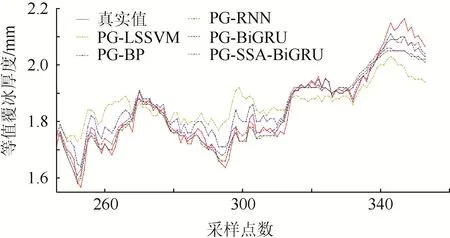
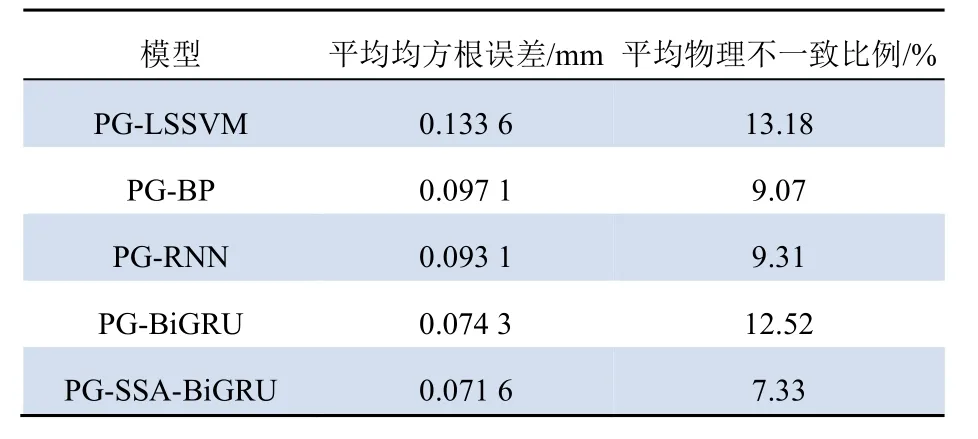
式中:t表示当前迭代;Cmax为最大迭代次数;α∊(0,1],为随机数;R2∊[0,1],为报警值;T∊[0.5,1],为安全阈值;Q为随机数,服从标准正态分布;L为1×d的全1 矩阵。当R2 加入者利用发现者来获取食物,加入者的位置更新见式(16)。 式中:Ap为发现者当前的最佳位置;Aw代表当前最差位置;B为1×d的矩阵。各元素随机赋值1或–1,且B+=BT(BBT)–1。 群体遇到危险时,麻雀群体互相靠近保证安全。表达式见式(17)。 式中:Abest为全局最优位置;β为步长控制参数,符合均值为0、方差为1 的正态分布;K∊[–1,1],为随机数;fi、fg和fw分别表示个体适应度值、全局最优和最差适应度值。为避免分母为0,加上最小常数ε。 针对梯度消失、无法捕获长期依赖关系的问题,GRU 对循环神经网络(recurrent neural network,RNN)做出了改进,且GRU 的2 个门结构(更新门、重置门)[21-23]相比LSTM 的3 个门结构(输出门、遗忘门、输出门)减少了需训练的参数,从而在保证精度的前提下提高了网络的训练速度。 对覆冰现象进行分析,发现覆冰状态随着时间不断发生变化;因此在研究覆冰问题时要考虑时序性。针对覆冰序列的非线性等时间序列性质,同时为了更好地利用未来和过去的信息,本文采用BiGRU:2 个独立的GRU 以前向、后向组合,其中一个模型正向读取输入序列,另一个反向读取输入序列,见式(22);然后将每个隐藏状态连接起来,即构成了BiGRU,如式(23)所示。 式中:zt为更新门;rt为重置门;xt为当前输入;为输入和过去隐藏层状态的结合;ht为隐藏层输出;Wz,Wr,Wh为可训练参数矩阵。 式中:T为序列长度。 采用SSA 算法对BiGRU 进行优化时,首先将其批处理大小、2 层隐藏层单元数目、最大迭代次数作待优化超参数,且在训练过程根据式(13)进行物理引导;然后再使用优化后超参数构建SSA-BiGRU 预测模型。完整的PG-SSA-BiGRU模型的构建流程如图4 所示。 图4 预测模型构建流程Fig.4 Construction process of prediction model 实验数据选取某监测站的覆冰监测数据,其中包含微气象因素温度、湿度、风速以及物理参量风偏角、综合悬挂荷载等监测数据;数据采集间隔为1 min,共24 h。截取其中某日覆冰增长期间6 h 的数据,共360 条数据,部分数据见表1。 表1 部分覆冰数据Tab.1 Partial icing data 首先清洗数据,根据覆冰形成时的基本气象条件去除掉异常值,如对温度大于5 ℃,相对湿度小于80%的数据进行剔除;然后采用线性插值法对缺失数据进行补全;最后使用最值归一化对数据量纲进行统一。以前70%作训练集,剩余部分作为测试集,其中综合荷载、风偏角数据取前70%用于训练过程中的物理引导。测试过程中使用温度、湿度、风速作为特征,以等值覆冰厚度作为标签输入模型中,且测试时采用平均绝对误差、均方根误差来反应预测模型的预测准确度并根据1.2 节修正方法判断物理不一致性。 如上文所述,数据中存在着无法判断是否符合物理规律的情况,除上述总结物理规律不能适用于所有数据采样点外,数据本身的精度不高导致许多相邻数据采样相等,变化量为零也会影响可判断数据点的数量,因此物理不一致的数据点分别占测试集和测试集中可判断是否符合物理规律的比例不同。评价指标中物理不一致性比例统一采用占整体数据集的比例。 对比实验一。第一组对比实验中,LSSVM 采用RBF 核函数,设惩罚系数为100,核函数宽度为30;BP 设定学习率为0.01,隐藏层神经元个数为12,最大迭代次数设置为500;RNN、BiGRU设置为隐藏层单元数目为64 的双层结构,批处理大小为32、时间步长和最大迭代次数取5 和120;SSA-BiGRU 时间步长取5,其他参数采用优化后参数。设置SSA 算法中批处理大小、隐藏层单元数目、最大迭代次数取值范围分别为[30,70]、[50,100]、[100,200],算法优化后各参数取值分别为39;63;88;103。第一组对比实验结果如图5。 图5 对比实验一的计算结果Fig.5 Calculation result of comparative experiment one 实验一中,LSSVM 和BP 偏差较大,其他模型均预测出了覆冰数据的整体走向,其中RNN 相较于BiGRU 和SSA-BiGRU 误差相对大,BiGRU和SSA-BiGRU 在数据细微波动时拟合较好,但BiGRU 在数据集尾部预测偏差较大,SSA-BiGRU整体效果优于BiGRU。可以看出BiGRU 模型相比于LSSVM、BP 在覆冰预测上效果更好,且SSA优化也对模型效果有所提升。 对比实验二。第二组对比实验中,LSSVM、BP、RNN、BiGRU、SSA-BiGRU、物理引导的LSSVM、BP、RNN、BiGRU 模型参数同实验一,物理引导SSA-BiGRU 模型时间步长取值同上,其他参数经优化后分别为32;79;93;112。对比实验二结果如图6 所示。 图6 对比实验二的计算结果Fig.6 Comparative calculation results of experiment two 实验二中加入物理引导后,LSSVM、BP 预测准确度提升较为明显,RNN、BiGRU、SSA-BiGRU预测准确度稍有提升。物理引导的SSA-BiGRU 模型对覆冰预测效果较好:预测结果在数据波动处拟合较好,且在数据末尾偏差最小,在预测最后也可以保证较高的精度。 在可判断数据有限的情况下,实验二中采用物理引导方法的各模型物理不一致性均有显著降低,具体数据如图7 所示。 图7 实验二模型物理不一致性占比Fig.7 The proportion of model physics inaccuracy in experiment two 由图7 可以看出:物理引导的LSSVM、BP、RNN、BiGRU、SSA-BiGRU 模型相比LSSVM、BP、RNN、BiGRU、SSA-BiGRU 模型物理不一致比例分别降低 56.31%、58.25%、45.63%、48.55%、40.77%;平均绝对误差分别降低0.142 7、0.061 8、0.034 9、0.024 6、0.004 8;均方根误差分别降低0.162 2、0.099 1、0.036 6、0.030 9、0.004 5。PG-SSA-BiGRU 模型在覆冰预测上有较高的准确度和物理一致性。整体实验结果评价见表2。 表2 实验二结果评价Tab.2 Results evaluation of experiment two 为验证模型普遍适用性,将24 h 数据等分5 份,并采用五折交叉法对“对比实验二”中各模型进行交叉验证,选取其中一个子集作为测试集,其他4 个子集作为训练集进行实验,并保证每一个子都作为测试集进行了实验,共进行5 次实验,得到5 次实验的均方根误差和物理不一致比例均值。交叉验证结果见表3。 表3 交叉验证结果Tab.3 Results of cross validation 交叉验证各模型结果相较于对比实验二预测准确度略微下降,物理不一致比例略微提升,但交叉验证中模型预测结果表现较为稳定,其中PG-SSA-BiGRU 模型保持了较高的预测准确度和较低的物理不一致性。 (1)本文根据覆冰序列的时间序列性质,采用BiGRU 构建覆冰预测模型,同时使用SSA 对BiGRU 模型超参数进行优化。通过实验验证了SSA-BiGRU 模型在覆冰预测上比LSSVM、BP、RNN、BiGRU 有着更高的预测准确度。 (2)基于物理引导的神经网络的思想需要有物理客观事实的支撑。对输电塔线在风冰荷载的条件下进行受力分析,总结出由预测覆冰厚度、风偏角推导综合荷载的变化趋势应同实际综合荷载变化趋势相一致的规律。采用损失函数,以综合荷载、风偏角监测数据对模型训练过程进行引导。实验中,由于判断方法、数据精度等原因导致总结规律只适用于覆冰数据中的部分采样点,但物理引导在预测模型的训练过程中起到了一定引导作用。最终的实验表明,构建的PG-SSA-BiGRU模型较大程度提高了覆冰预测的准确性。 (3)针对实验阶段得出的数据精度不高,导致可判断是否符合物理规律的数据采样点有限的问题,后续可以通过采用数据变化较大的数据,以及尝试提升采集数据所用传感器精度的方法改进后再进行实验。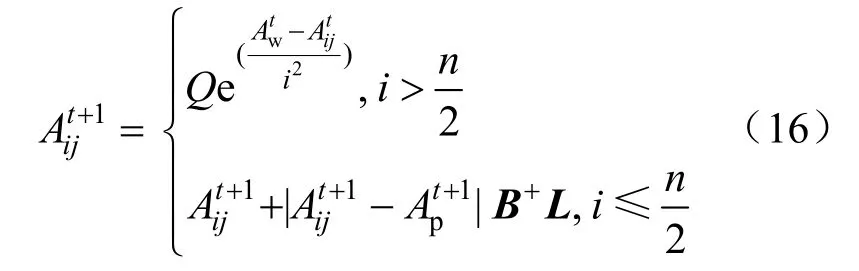
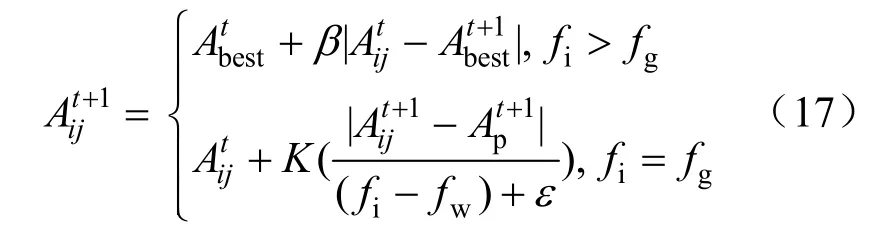
2.2 双向门控循环单元



2.3 预测模型构建流程

3 实验验证




4 结论
