HHT结合QPSO-GRNN的同塔双回输电线路故障测距

2022-03-04于仲安张军令

电力科学与工程 2022年2期

于仲安，陈苗，张军令

（江西理工大学电气工程与自动化学院，江西赣州 341000）

0 引言

同塔双回线技术在电力系统应用广泛[1]。在同塔双回线线路出现故障时，及时精准地计算出故障位置对于维持系统的稳定性、降低经济损失十分重要。计算故障位置的方法现主要有2 类，即故障分析法与行波测距法。前者结合线路参数、故障参数、线路模型及序网图进行大量的计算，进而得到故障位置：这种方法计算比较复杂[2-3]。行波法利用采集到的线路单端或者双端故障初始行波波头到达的时间数据，结合故障测距公式，经计算得到测距结果。相对于故障分析法，行波测距法计算量小，但是计算中存在波速不确定、双端法波头到达两端时间不能严格同步等问题[4-5]。

人工智能的迅速发展使得模拟人脑工作原理的神经网络成为研究热点。在输电线路测距过程中，通过神经网络可以在对大量样本训练后找到输入与输出之间的关系并建立模型，进而实现预测出输出值。目前，这方面的研究方向多集中在直流线路，交流线路仅针对单回线。文献[6]将蚁群算法和Elman 神经网络结合，用于直流线路测距；但是该方法存在输入样本固有主频率难以提取的问题。文献[7]发现，使用径向基函数（radial basis function，RBF）在数据样本比较少时测距精度不高。文献[8]将从交流线路两端采集的电压信号进行S 变换，变换结果作为数据源输入至测距函数，并采用粒子群优化（particle swarm optimization，PSO）算法进行测距；由于PSO 需要设置的参数过多，随机性和不确定性强，导致粒子的速度不能得到很好的控制，易陷入局部最优解。

针对上述问题，在故障信号处理时，本文提出将希尔伯特黄变换[9]（hibert-huang transform，HHT）与智能算法中的量子粒子群（quantum particle swarm optimization，QPSO）优化广义回归神经网络（generalized regression neural Network，GRNN）（后文简称QPSO-GRNN）相结合，对同塔双回交流输电线路进行故障测距：以电流特征模量希尔伯特黄变换所得采样点为模型训练过程中的输入，对应故障距离为输出，训练得到最优光滑因子和测距模型。

1 QPSO-GRNN 模型

1.1 GRNN 模型

GRNN[10]是在RBF 的基础上进行改进得到的，其特点是：具有很强的非线性映射能力；在样本较少时仍能得到较好的预测效果；泛化能力强，网络结构简单，需要调节的参数少。

设x是自变量，y是因变量，其联合概率密度为f(x,y)，x、y观测值分别记为X，Y。Y的数学期望见式（1）：

设输入样本x的维度为d，输出维度为k，光滑因子为σ。当训练样本数为n时，经Parzen 非参数估计可得式（2）：

将式（4）代入式（3）中，可得式（5）：

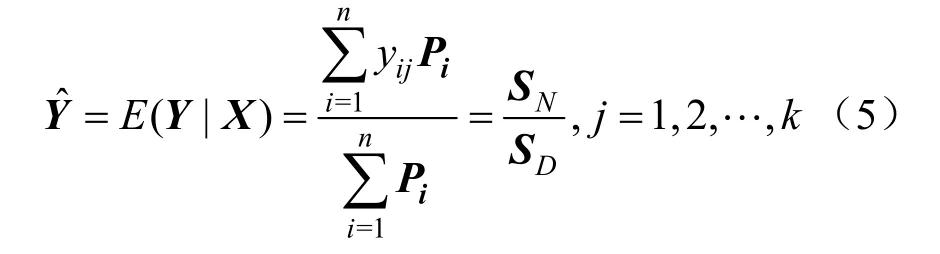
GRNN 模型分为4 层，如图1 所示。输入层用于接收样本，且输入端口数与输入样本维数保持一致；在模式层将样本处理完后，结果传递给求和层；在求和层，将各个样本进行直接求和及加权求和；在输出层，最终将加权求和结果与直接求和结果的比值输出。

图1 GRNN 模型结构Fig.1 GRNN model structure

对于GRNN，仅需调节适应函数的光滑因子σ的大小，就可改变模型输出的效率及精确度；但光滑因子σ的选择仍受人为因素的影响。当σ过小时，拟合能力较强，但泛化能力较弱，预测效果较差；当σ过大时，拟合能力、泛化能力和预测效果与σ过小时的结果相反。

为获得最优的GRNN 模型，需寻找到最优的光滑因子σ。因此，通过引入量子粒子群优化算法对GRNN 模型中的最优光滑因子进行寻找。

1.2 基于QPSO 算法的GRNN 模型优化

标准粒子群算法中，粒子寻求最优解时易陷入局部最优。针对此缺陷，文献[11]提出了一种模拟物理学中微观粒子运动行为的量子粒子群优化算法。

与标准粒子群相比，量子粒子群全局极值搜索能力更强，需要设置的参数更少。由于粒子在微观世界中不存在质量与惯性，因而其速度及位置值无法同时被精确观测。由此，可利用波函数的统计属性来估算粒子出现在空间某处的概率。用Schrodinger 方程计算概率密度，再使用Monte Carlo 随机数法更新粒子位置。

假设d维空间中有m个粒子，表示第i个粒子迭代至t次，在第j(j=1,2,···,d)维的位置，则更新公式如下：

式中：u和ϕ随机分布在0～1 之间；α为QPSO 中的创新参数，一般取不大于1 的正实数。调节α便可改变粒子收敛速度；在QPSO 的粒子优化过程中，表示第i个粒子迭代更新至t次，第j维获得的历史个体最优σ，分别表示粒子群迭代更新至t次，第j维获得的历史整体最优σ以及个体最优σ的平均值；为吸引子，用于吸引粒子靠近。可根据式（7）（8）更新。QPSO 优化目标函数如式（9），所求为模型预测输出值与实际值的最小均方差：

式中：emin表示最小均方差，需人为设置；y预测,i和y实际,i分别为模型训练过程中预测输出值和实际值。QPSO-GRNN 模型故障测距流程如图2。

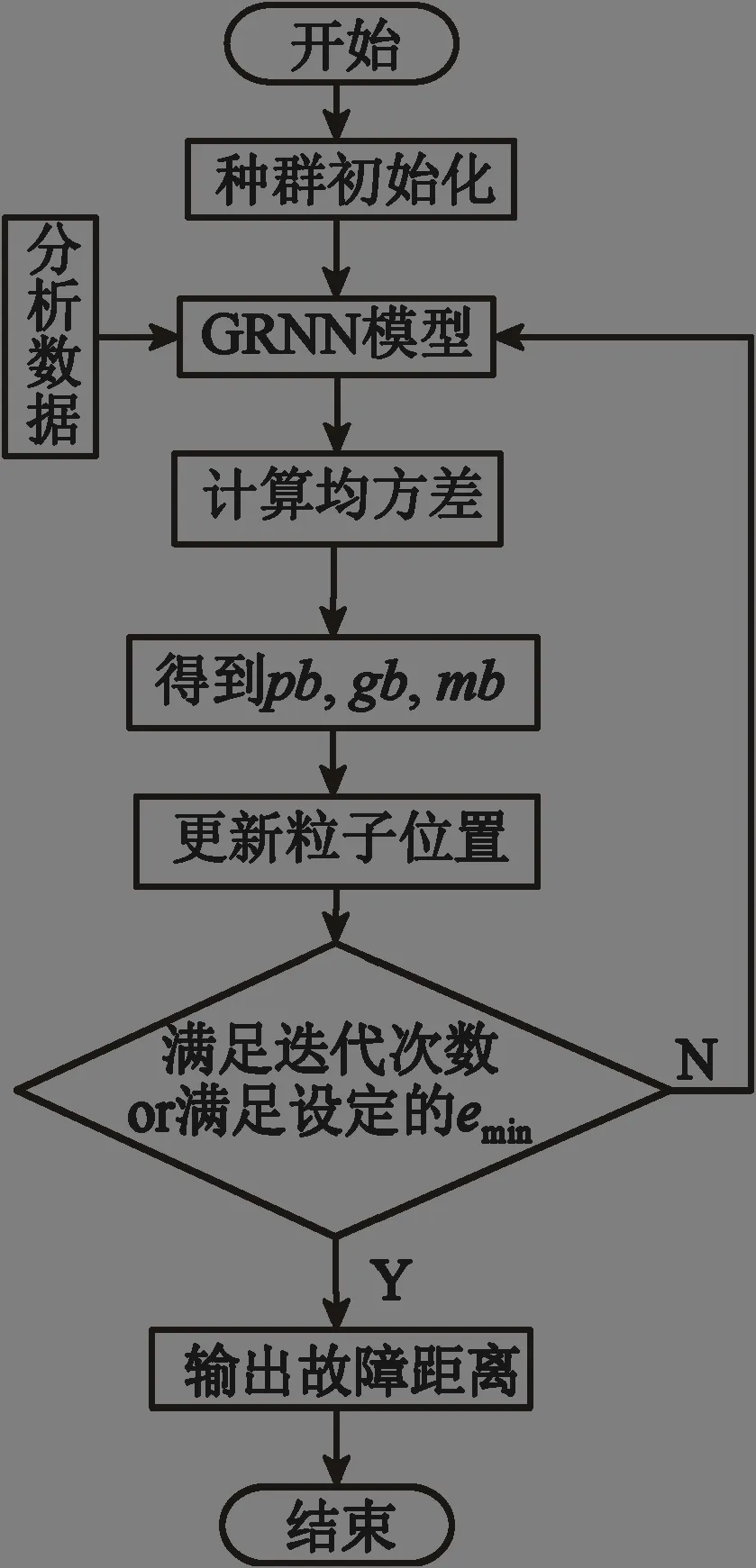
图2 QPSO-GRNN 模型故障测距流程Fig.2 QPSO-GRNN model fault location process

1.3 输入样本的获取

不对称参数同塔双回线的系统结构如图3 所示。系统由两端电源P、Q 供电，M、N 为同塔双回线两端。双回线各阻抗符号见表1。

表1 线路阻抗符号含义Tab.1 Symbolic meaning of line impedance

图3 同塔双回线系统结构图Fig.3 Structure of double circuit lines on the same tower system

同塔双回线各相电压、电流及阻抗的关系如式（10）：

式中：U、I表示线路电压和电流；下标I、Ⅱ为线路标号；A、B、C 代表线路的三相。

相比于单回线，同塔双回线方式节约输电走廊，提高了输电效率；但其相间和线间存在复杂的耦合，使得传统的应用在单回线上的保护不能直接用在双回线上，因此：首先需要对双回线参数进行解耦。引用文献[12]中的矩阵S对双回线进行解耦。因双回线参数不对称，需引入不对称参数K1、K2，得到总解耦矩阵M如式（11），解耦后得到电流模量I1—I6如式（12）所示。

式中：

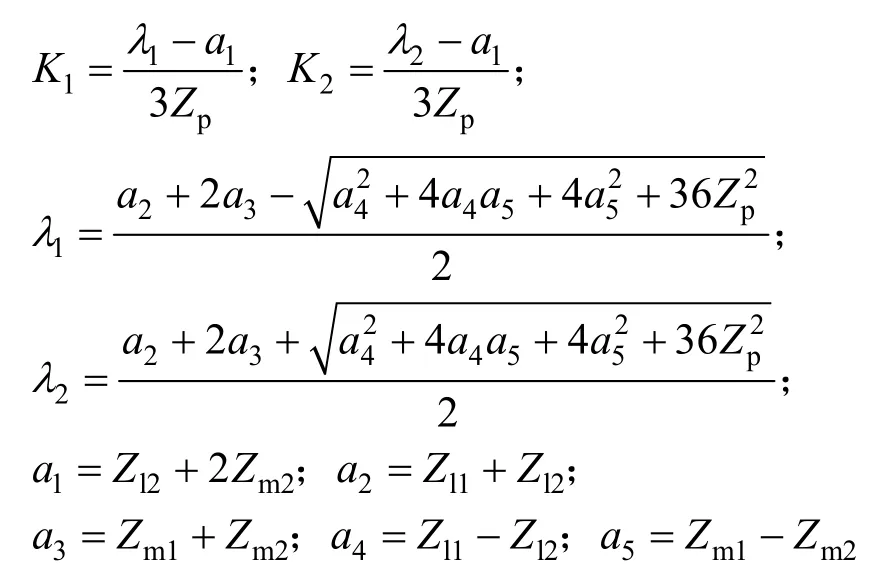
根据式（12），模量1 和4 与I、Ⅱ回线均相关，模量2 和3 只与I 回线故障有关，模量5 和6只与Ⅱ回线故障有关，因此：模量2、3、5 和6可作为特征模量来判断发生故障的线路。理想情况下，若只有线路I 故障，模量5 和6 数值应为0，模量2 和3 数值大于0；同理可得，当线路Ⅱ故障，若为跨线故障，4 个模量均大于0。

考虑到工程实践中存在各种因素引起的不平衡电流，所以线路I 故障时，模量5 和6 数值并不为0；因此需设置一个门槛值ε1，保证在不平衡电流达到最大时也可不发生误判。

定义2 个参数g1、g2：若g1=max{|I2|,|I3| }﹥ε1，则I 回线故障；若g2=max{|I5|,|I6|}﹥ε1，则Ⅱ回线故障。设置电流门槛值ε1= 0.2% × max{g1,g2}。根据ε1、g1、g2可判断是否发生故障及故障时的线路。

确定故障线路后，选取对应的电流特征模量进行希尔伯特黄变换。希尔伯特黄变换由经验模态分解（empirical mode decomposition，EMD）和希尔伯特变换（hilbert transform，HT）2 部分组成。希尔伯特变换要求信号必须满足线性且稳态这2 个条件。工程实践中所获得的信号大多只能满足这2 个条件其中一个，或无法满足其中任一条件。EMD 的出现解决了这个问题：通过将输入信号分解成多个固有模态函数（intrinsic mode function，IMF）分量，使其满足希尔伯特变换要求；然后进行希尔伯特变换，即可得到故障初始行波到达两端信号采集装置的采样点。以2 个采样点作为QPSO-GRNN模型的输入，故障距离为模型输出，通过样本对模型进行训练，可得出采样点与对应故障距离间的映射关系，实现模型故障测距。

2 仿真分析

在仿真软件PSCAD 中搭建参数不对称的同塔双回线系统模型，如图4 所示。

图4 参数不对称同塔双回线系统模型Fig.4 System model of asymmetric parameters double circuit transmission lines on the same tower

部分参数设置界面如图5 所示，图中电压等级500 kV，频率50 Hz，A 相发生接地故障。

图5 仿真参数设置Fig.5 Simulation parameter setting

设置线路全长300 km，采样频率1 MHz，0.05 s处发生故障，故障持续0.02 s，仿真过程持续0.1 s。线路的具体参数见表2。

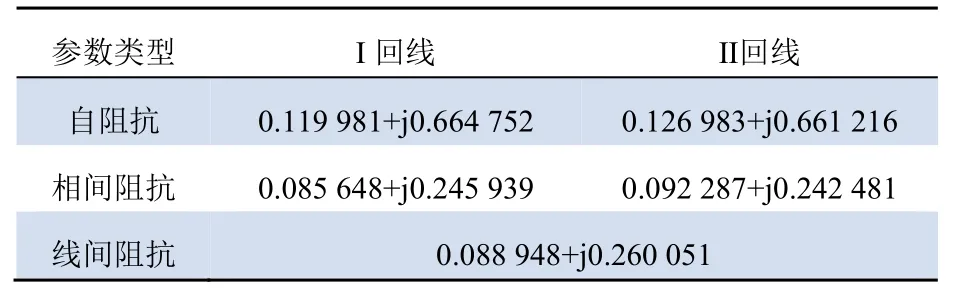
表2 线路参数Tab.2 Circuit parameters Ω/km

以第Ⅰ回线16 km 处A 相接地故障为例。采集线路两端故障发生后0.02 s 的电流数据，并在MATLAB 中进行处理。图6 为两端模量I3经验模态分解结果，图中r表示无法再进行IMF 分量提取的剩余信号。图7 所示为通过希尔伯特变换获得的时间–频率特性曲线。根据传统的双端行波测距公式可以估算出故障位置。公式如式（13）所示。

图6 经验模态分解结果Fig.6 Empirical modal decomposition results

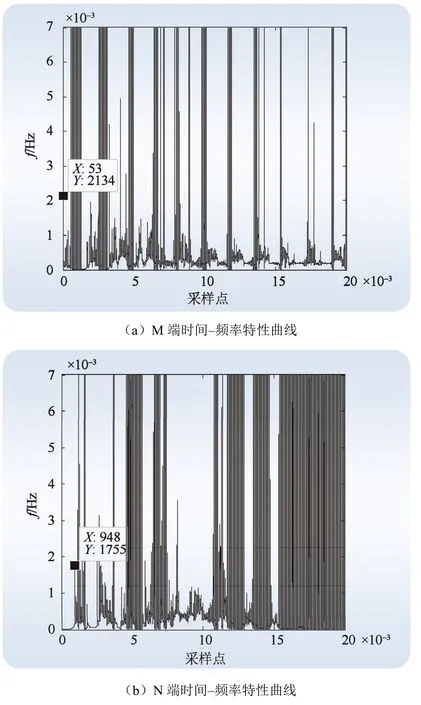
图7 时间–频率特性曲线Fig.7 Time-frequency characteristic curves

式中：L为线路全长；v为波速，近似取光速；tM和tN分别表示故障行波波头初始到达M、N 端的时刻；dM和dN分别表示故障处距离M、N 端的距离。

因采样频率设置为1 MHz，采样点53 和948分别对应53 μs 和948 μs。根据式（13）计算得到的故障位置为15.75 km，测距误差0.25 km。

因根据传统行波双端测距公式所得测距误差太大，故提出：将其与智能算法相结合。点53 和948 可作为一组训练样本的输入，16 km处数据为测距模型对应的输出。在模型进行训练时，以5 km 处为起点，每隔5 km 采样一次，将过渡电阻分别设置为0 Ω，10 Ω，100 Ω；故障类型选取4 种，共590 组样本，具体样本见表3。以PSO 算法结合GRNN（后文简称PSO-GRNN）模型作为对比，任选其中 509 组样本输入到PSO-GRNN 和QPSO-GRNN 模型中进行训练，剩余81 组进行测试。

表3 故障样本数Tab.3 Number of failure samples

2.1 迭代次数对比分析

为更好地分析QPSO 和PSO 寻优过程中迭代次数的变化，在MATLAB 中对PSO-GRNN 和QPSO-GRNN 进行训练。程序中设置迭代终止条件为最小均方误差emin≤0.004 km 或迭代次数达到200 次。经过大量实验，PSO 和QPSO 粒子数最终均设定为20；PSO 中惯性权重ω=0.6，加速因子c1=2，c2=2；QPSO 中α=0.6。2 种模型训练迭代收敛曲线如图8 所示。

根据图8 可知，QPSO 迭代64 次后，达到由程序设置的均方误差值，完成收敛；而PSO 则在迭代115 次后完成收敛。由此验证了：QPSO 相比于PSO 收敛能力更强，速度更快。

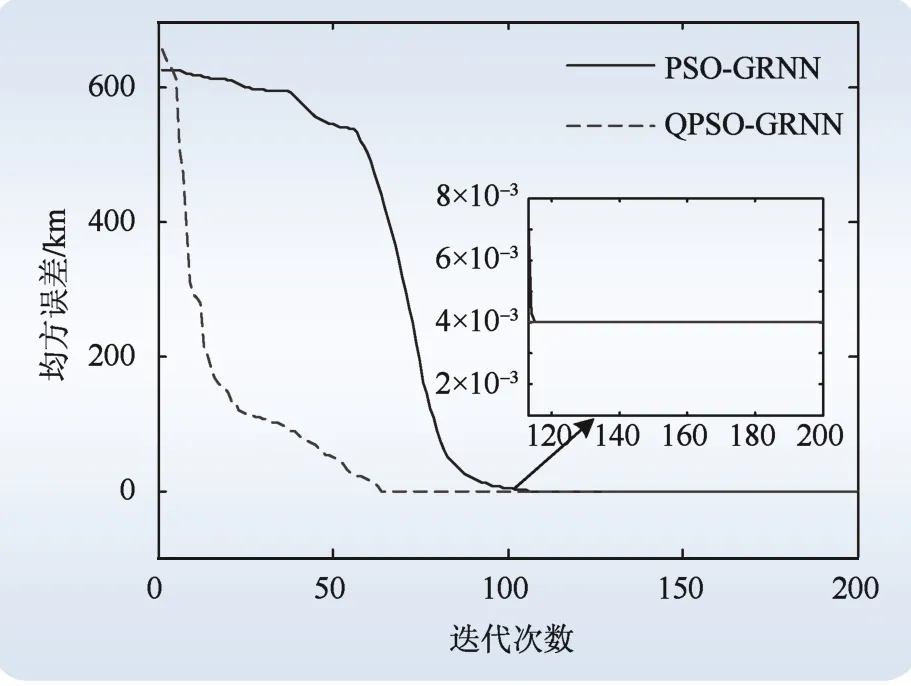
图8 2 种模型迭代收敛情况对比Fig.8 Comparison of Iteration convergence between two models

2.2 故障测距误差对比分析

将81 组样本代入模型进行检验。图9 为测试样本采用PSO-GRNN、QPSO-GRNN 及HHT 结合传统双端行波法（见公式（13），简称HHT）测距的误差对比图。

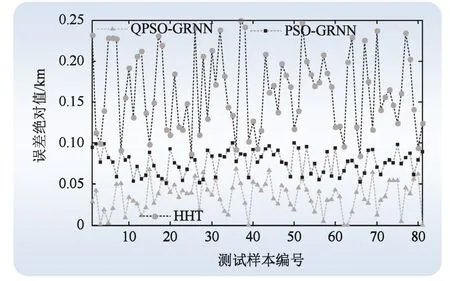
图9 故障测距误差对比结果1Fig.9 The first comparison fault location error

从图9 可以看出：QPSO-GRNN、PSO-GRNN和HHT 这3 种方法最大测距误差分别为0.074 km、0.1 km 和0.25 km。QPSO-GRNN 模型误差最小；除个别测试样本外，其整体测距效果优于PSO-GRNN。HHT 测距误差最大。这证明了行波法与智能算法结合，可以克服双端行波法采样误差、行波波速不确定等因素对测距结果带来的影响；经QPSO优化的算法同时也克服了PSO容易陷入局部最优解的缺陷。相比990 组[13]和1 500 组[14]训练样本，GRNN 仅采用509 组就可达到较好的测距效果，从而验证了其具有较强的泛化能力。

将模型推广至参数对称同塔双回线情况。任意选取20组测试样本代入已经训练好的测距模型中，并与2 种行波测距法，即HHT 和小波变换[15]（wavelet transform，WT）做对比。其中WT 测距原理同HHT，利用两端采样点结合测距公式（13）可得到故障距离。3 种方法测距误差如图10 所示。据图10 可知，QPSO-GRNN、WT、HHT最大测距误差分别为0.069 km、0.15 km、0.21 km，且QPSO-GRNN 整体测距误差小于HHT 和WT：这证明了所得模型测距效果优于2 种行波法，且针对参数不对称同塔双回线的测距模型对参数对称同塔双回线也具有较强的适用性。

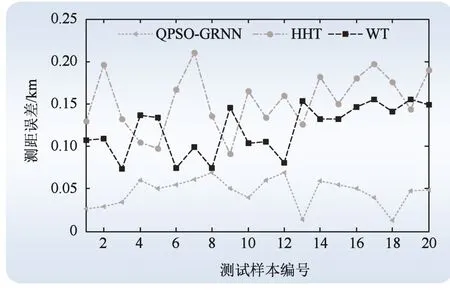
图10 故障测距误差对比结果2Fig.10 The second comparison fault location error

用PSACD 仿真得到的样本是建立在无噪声干扰的理想情况下的。为了满足工程实践的要求，将40～50 dB 的高斯白噪声加入训练样本中训练，使QPSO-GRNN 模型具有一定的抗干扰能力；再将45 dB 的高斯白噪声加入至测试样本中。由图11 可观察到，模型测距误差绝对值最大为0.083 km。这说明模型具有较好的抗干扰能力，能满足一定的工程需求。