抑制钢轨波磨的梯形轨道结构的多参数拟合与优化

崔晓璐，李童，漆伟

抑制钢轨波磨的梯形轨道结构的多参数拟合与优化

崔晓璐1，李童1，漆伟2

（1.重庆交通大学 机电与车辆工程学院，重庆 400074；2.重庆市轨道交通（集团）有限公司，重庆 401120）

研究地铁车辆结构一系悬挂及轨道结构支承刚度和阻尼对梯形轨道小半径曲线钢轨波磨的影响规律，并提出抑制相应区段钢轨波磨的多参数拟合优化方法。基于轮轨系统的摩擦自激振动理论，构建梯形轨道小半径曲线段上带有一系悬挂轮轨系统的有限元模型。然后通过复特征值分析，研究地铁梯形轨道小半径曲线段轮轨系统的摩擦自激振动特性。最后开展地铁车辆结构一系悬挂及轨道结构支承刚度和阻尼的参数化分析，采用最小二乘法，对影响不稳定振动的关键参数进行多参数拟合。根据该拟合方程，采用遗传算法进行关键参数的优化匹配。在曲线半径为350 m的梯形轨道上，轮轨间因存在饱和蠕滑力，引起摩擦自激振动，在439.02 Hz时，产生了不稳定振动，从而导致了钢轨波磨的产生。影响轮轨间不稳定振动的关键因素为扣件的垂向刚度、横纵向刚度、垂向阻尼和减振材料的垂向刚度。当扣件的垂向刚度为36 MN/m、扣件的横纵向刚度1.68 MN/m、扣件的垂向阻尼为2.9 kNs/m、减振材料垂向刚度为5.57 MN/m时，可有效抑制梯形轨道小半径曲线段上钢轨波磨的发生。

钢轨波磨；梯形轨道；摩擦自激振动；复特征值分析；多参数拟合；遗传算法

轨道减振结构常铺设在振动噪声多发的轨道区段，在投入使用一段时间后，这些轨道减振结构区段普遍产生了钢轨波磨，特别是小半径曲线段的钢轨波磨尤为严重[1-2]。以梯形轨道结构为例，该轨道上出现的钢轨波磨不仅降低了梯形轨枕的减振效果，还进一步增大了地铁车辆运营时产生的振动噪声，加速了车轨零部件的损害，增加了维护成本，严重时还会危及行车安全，故亟需解决。

近年来，许多学者对钢轨波磨这一典型的钢轨病害问题开展了研究。钢轨波磨是一种钢轨顶面上周期性不平顺的轮轨接触疲劳破坏，其形成机理较为复杂。目前普遍认可的钢轨波磨产生机理是Grassie[3-4]提出的钢轨波磨基本理论，其内容主要包括表现振动特性的固定波长机理和表现磨损特性的损伤机理，同时对目前已知的钢轨波磨进行分类解释，并提出对应的治理方式。为抑制不同轨道减振结构区段处上钢轨波磨的产生，国内外许多学者针对不同减振结构区段处的钢轨波磨开展了机理性的研究，进行了多种参数的分析与优化。闫子权和Markine等[5-6]通过对北京地铁车辆轨道系统的动态仿真，对梯形轨道的动态特性进行了优化分析，以控制钢轨振动，提出减小钢轨波磨的梯形轨道结构参数优化建议。肖宏等[7]通过构建车-轨-隧动力学模型，研究了4种轨道结构上的钢轨波磨发展过程，通过参数分析，研究了车速、轮轨摩擦系数等因素对波磨产生的影响。雷震宇等[8-9]研究了科隆蛋扣件轨道上钢轨波磨的产生机理，验证了车速对波磨增长率曲线的特征频率无影响，车速提高将增大波磨波长与发展速度。Oyarzabal、Correa等[10-11]对3种不同轨道进行了钢轨波磨增长的研究，并对其按照钢轨波磨的增长趋势进行排序，并提出通过调整减振结构参数以减小波磨的参数优化方法。可以发现，以上研究主要是针对不同参数对减振轨道上钢轨波磨产生的影响以及对应的优化方法，较少考虑到减振轨道结构多种参数之间的相互联系对钢轨波磨生长的影响。

考虑到多种参数之间的相互联系，为抑制梯形轨道上发生的钢轨波磨，本文开展了以下工作：

1）通过现场调研，发现成都地铁铺设梯形轨枕处产生了明显的波磨，且小半径曲线段的短波波磨病害十分明显，主要发生在低轨轨面上。为研究钢轨波磨产生的动力学成因，基于摩擦自激振动理论和现场调研数据，建立了梯形轨道小半径曲线钢轨波磨发生区段上带有一系悬挂轮轨系统的有限元模型，通过模型的有限元分析，确定地铁梯形轨道小半径曲线段轮轨系统的摩擦自激振动特性。

2）根据建立的有限元模型，开展地铁车辆结构一系悬挂及轨道结构支承刚度和阻尼的参数化分析。

3）采用最小二乘法，对影响不稳定振动的关键参数进行拟合，进而采用遗传算法进行了关键参数的优化匹配。根据优化结果，提出抑制钢轨波磨的方法。

1 仿真模型与数值方法

1.1 钢轨波磨高发区段的现场调研

通过成都地铁线路的现场调研发现，在梯形轨枕区段出现了严重的波磨问题，主要发生在小半径曲线的低轨区段，如图1所示。该路段为典型的小半径曲线上梯形轨道受钢轨波磨的病害路段，轨道曲线半径为350 m。经测量，该区段钢轨波磨的波长为30～60 mm，为典型的短波波磨。此外，该线路采用DTVI 2型扣件，地铁车型为A型，列车通过该区段的速度为60～ 80 km/h。由此可以预测诱导钢轨波磨产生的主要频率范围为277.8～740.8 Hz。

图1 小半径曲线段波磨

1.2 轮轨系统的接触模型

为进一步研究梯形轨道小半径曲线上波磨的发生机理，根据现场的地铁车辆轨道结构，构建了小半径曲线段上的轮轨接触模型，如图2所示。轮轨系统的接触模型主要结构包括转向架构架、轮对、钢轨、轨枕、地基。根据该模型，可以了解到含一系悬挂轮轨系统的接触位置、受力情况等细节。当车辆通过小半径曲线时，由于构架上方车体质量与向心力作用，一系悬挂上方受到簧上载荷[12-13]，即垂向载荷SVL、SVR，以及克服车体离心运动的横向载荷SLL、SLR。构架与轮对之间由一系悬挂连接，该一系悬挂采用纵、横、垂三方向刚度阻尼单元模拟，其垂向刚度和阻尼分别为SY和SY，横向刚度和阻尼分别为SX和SX，纵向刚度阻尼分别为SZ和SZ。对于轮轨接触位置，假设轮轨间的接触为单点接触，则外轨接触点位于车轮轮缘与钢轨轨头侧面处，而低轨接触点位于车轮踏面与钢轨轨头顶部。低轨上的接触角为R，高轨上的接触角L，钢轨轨底坡为1/40。钢轨与梯形轨枕由扣件连接，扣件由三方向的弹簧阻尼单元代替，其中其垂向刚度和阻尼分别为RY和RY，横向刚度和阻尼分别为RX和RX，纵向刚度和阻尼分别为RZ和RZ。梯形轨枕与地基间铺有减振材料，该减振材料的垂向支撑刚度和阻尼同样采用弹簧阻尼单元进行模拟，其垂向刚度和阻尼分别为P、p。

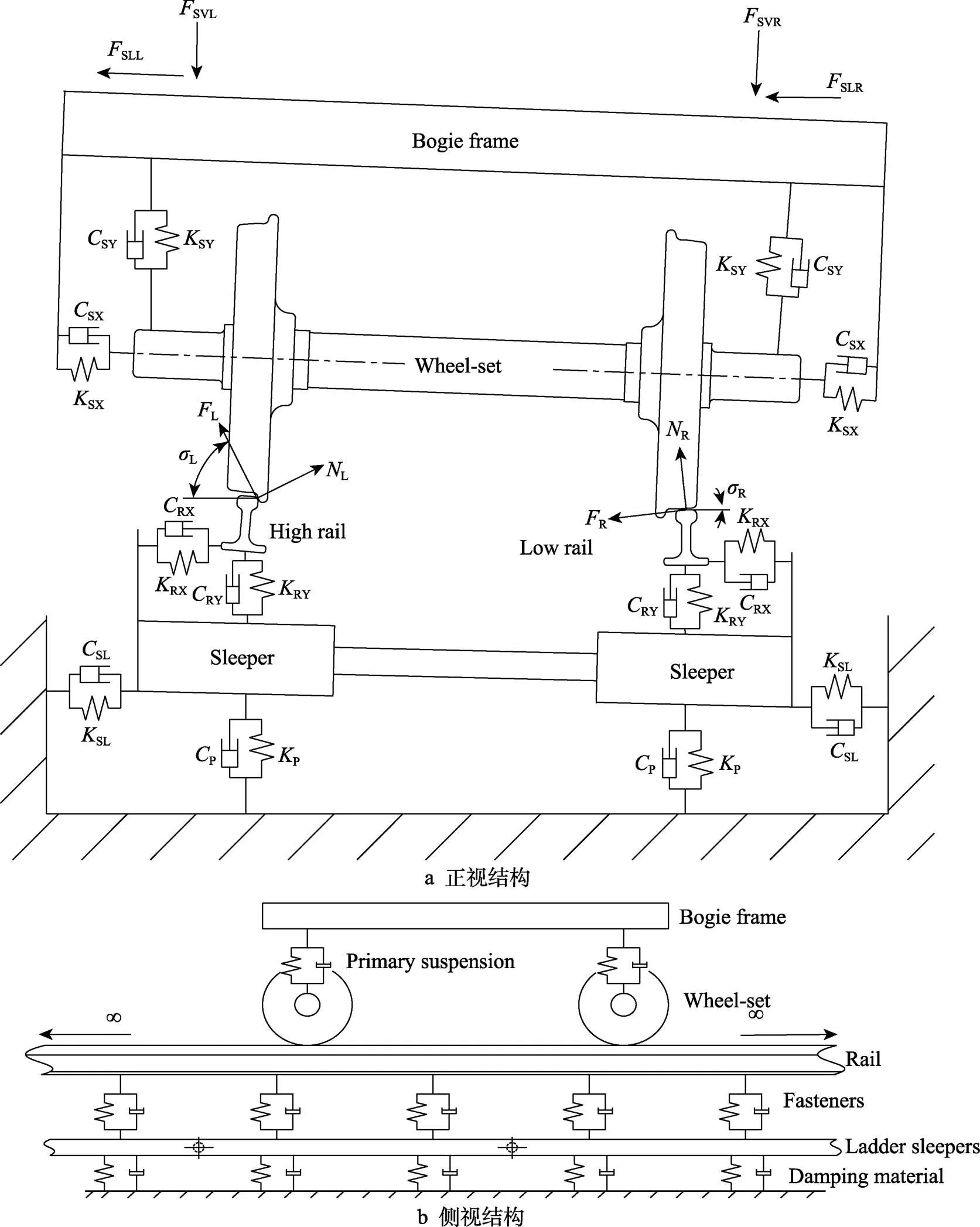
图2 梯形轨道上轮轨系统的接触模型

1.3 轮轨系统的有限元模型

为模拟出导致钢轨波磨产生的振动特性，本文根据轮轨接触模型，建立了梯形轨枕支撑的轮轨系统的有限元模型，如图3所示。该模型由转向架构架、轮对、钢轨、扣件和轨枕等组成，具体的材料参数见表1。转向架构架采用的是解析刚体结构，悬挂力加载在转向架两端，轮对结构和轨道结构均采用弹性体。在轮对结构中，两轮对采用LM踏面，车轮的轮径为840 mm，两轮对轴距为2300 mm。转向架构架与轮对间的一系悬挂由弹簧阻尼单元代替。在钢轨结构中，钢轨选用的规格为60 kg/m，轨底坡为1/40，钢轨两端采用固定边界条件，钢轨和轮对间的摩擦系数为0.4。在梯形轨枕的结构中，为使结果不会因为模型中钢轨过短而受该边界条件的影响，在钢轨之下设置5块梯形轨枕，每块长6150 mm，轨枕下的减振材料铺设间隔为1.25 m[14-18]。为简化模型，将减振材料由均匀布置的弹簧阻尼单元代替。钢轨和轨枕间由DTVI 2型扣件连接，为更好地模拟扣件，每个扣件均采用在连接位置设置若干均布的点对点弹簧阻尼单元代替。一系悬挂、扣件与减振材料的具体参数见表2。

图3 梯形轨枕支撑的轮轨系统有限元模型

表1 有限元模型材料参数

Tab.1 Material parameters of FEM

表2 悬挂和轨道支撑结构参数

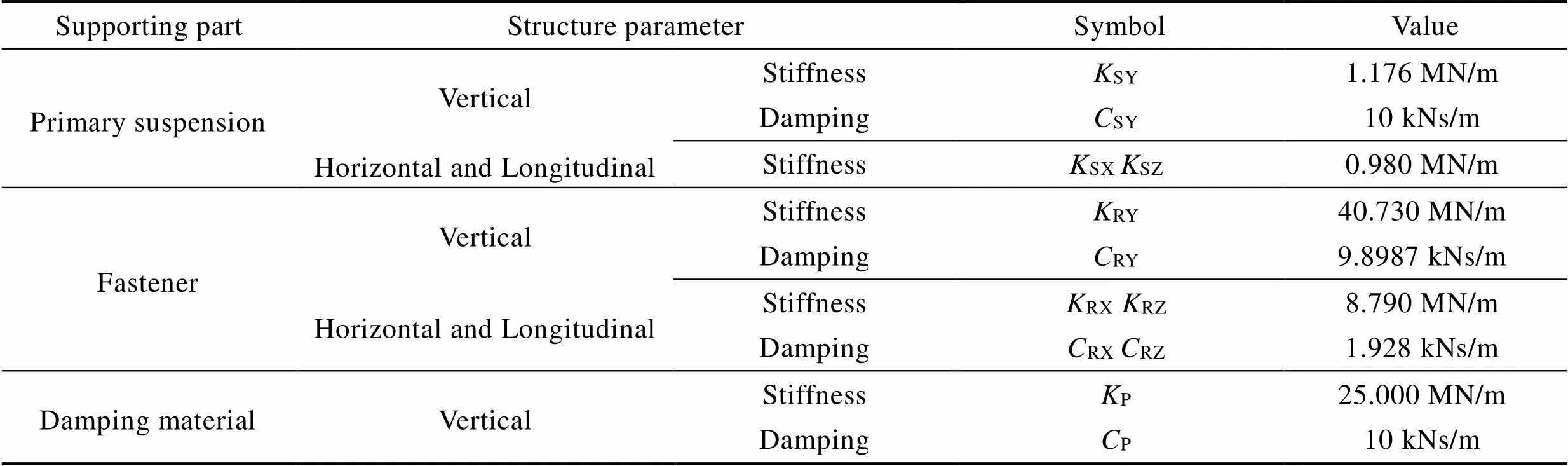
Tab.2 Suspension and support structure parameters

1.4 基于摩擦自激振动的有限元分析方法

根据摩擦自激振动的理论[19-20]，当列车行驶在梯形轨道支撑的小半径曲线路段上时，轮对与钢轨接触位置的蠕滑力通常趋于饱和，轮轨间的相对滑动致使滑动摩擦力的产生。该滑动摩擦力在轮轨接触界面上激励，并维持系统的非线性振动，进而轮轨间的法向接触力发生同频波动，使系统产生波动摩擦功，钢轨轨面产生钢轨波磨。本文采用复特征值分析的方法，预测自激振动发生频率的分布与其发生可能性的大小，即对应频率下的稳定性大小。

对于摩擦系统中相对运动的接触界面，主面上的有限元节点相对从面运动方程可表示为[21-23]：

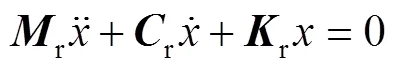
式中：代表位移；r、r、r分别代表在排除摩擦力对系统平衡位置处的动力学影响后的质量矩阵、阻尼矩阵和刚度矩阵。其中阻尼矩阵包含摩擦引起的阻尼效应与材料的阻尼特性。此外，由于摩擦的存在，刚度矩阵为非对称矩阵。

经拉式变换后，可得其特征方程：

由于刚度矩阵为非对称矩阵，导致系统存在复特征值与复特征向量。采用子空间投影法，将系统处于稳定时的状态作为子空间进行投影，并通过QZ分解求解该方程，变换至时域可得通解：

其中φ为第S阶特征值，且可表示为(α+jω)。一般而言，摩擦自激振动的发展趋势由等效阻尼比来评估：

(4)

由于实部α为正值，表示系统处于不稳定状态，故等效阻尼比为负值时，意味着振动的不稳定，且一般等效阻尼比越小，系统的不稳定性越大。当频率无变化时，也可以认为实部α越大，系统的不稳定性越大[24]。

2 轮轨系统的多参数拟合与优化

2.1 轮轨系统的摩擦自激振动特性

根据已建立的梯形轨道支撑的轮轨系统有限元模型，基于摩擦自激振动理论，通过复特征值分析法，可以获得摩擦自激振动发生时梯形轨道支撑的轮轨系统的频率与对应模态，如图4所示。可以发现，梯形轨枕上轮轨间的摩擦自激振动的主要频率为493.02 Hz，发生位置在低轨上。该地段上，地铁车辆的行驶速度为60～80 km/h。通过计算得出，在该频率下发生的钢轨波磨波长应为34～35 mm，与现场低轨上的钢轨波磨测量数据吻合，由此验证了该模型的准确性。

图4 轮轨系统的摩擦自激振动频率及其模态

2.2 轮轨系统的参数分析

根据以上有限元模型，本文以小半径曲线轨道梯形轨枕支承含一系悬挂的轮轨系统作为研究对象，研究车辆结构中一系悬挂及梯形轨道支撑结构中支撑刚度和阻尼等参数对轮轨间摩擦自激振动的影响。选取了10个轨道主要参数，为方便计算，每个轨道参数由基础值分别乘以系数0.2、0.6、1.0、1.4、1.8、2.2。这些参数与对应的基础值分别是：一系悬挂刚度垂向、横纵向的基础值均为1 MN/m；一系悬挂垂向阻尼，基础值为10 kNs/m；扣件刚度垂向、纵横向的基础值分别为40、8 MN/m；扣件阻尼垂向、横纵向的基础值分别为10、2 kNs/m；减振材料垂向刚度、阻尼的基础值分别为25 MN/m、10 kNs/m。研究采用复特征值分析，并以复特征值实部作为评定指标。当复特征值实部为正值时，该值越小，认为对应频率下的系统相对越不容易发生摩擦自激振动，即波磨发生的可能性相对越小。通过控制变量法，分别研究了这10个主要参数对等效阻尼比变化的影响。选取对照的控制变量为上述所选的基础值。

参数化分析的结果如图5所示。由图5a—c可知，一系悬挂参数对复特征值实部的影响较小。受一系悬挂垂向刚度增大的影响，复特征值实部先减小、后增大，并在调整系数为0.6（即0.6 MN/m）左右时取得最小值。随一系悬挂横向、纵向刚度的增大，复特征值实部基本没有变化，表明横向、纵向刚度的改变对不稳定振动无明显影响。复特征值实部随一系悬挂垂向阻尼的增大呈递增趋势，但增幅逐渐减小。根据图5d—g可以发现，不稳定性振动对扣件相关参数的敏感性较大。随着其垂向刚度的增加，不稳定性振动呈现先较快减小、后缓慢增加的趋势，并在调整系数为0.6（即24 MN/m）左右取得极小值。随扣件横向、纵向刚度的增加，不稳定性振动呈增加的趋势。不稳定性振动随扣件垂向阻尼的增加，呈先增大、后减小的趋势，并在阻尼为14 kNs/m左右取得极大值。不稳定性振动对扣件横向、纵向阻尼的敏感性相对较小，且随扣件横向、纵向阻尼的增大呈逐渐增大的趋势。根据图5j可知，不稳定性振动随减振材料垂向刚度的增加呈增大趋势，且增幅明显。根据图5i可知，随减振材料垂向阻尼的增大，不稳定性振动呈缓慢增加的趋势。

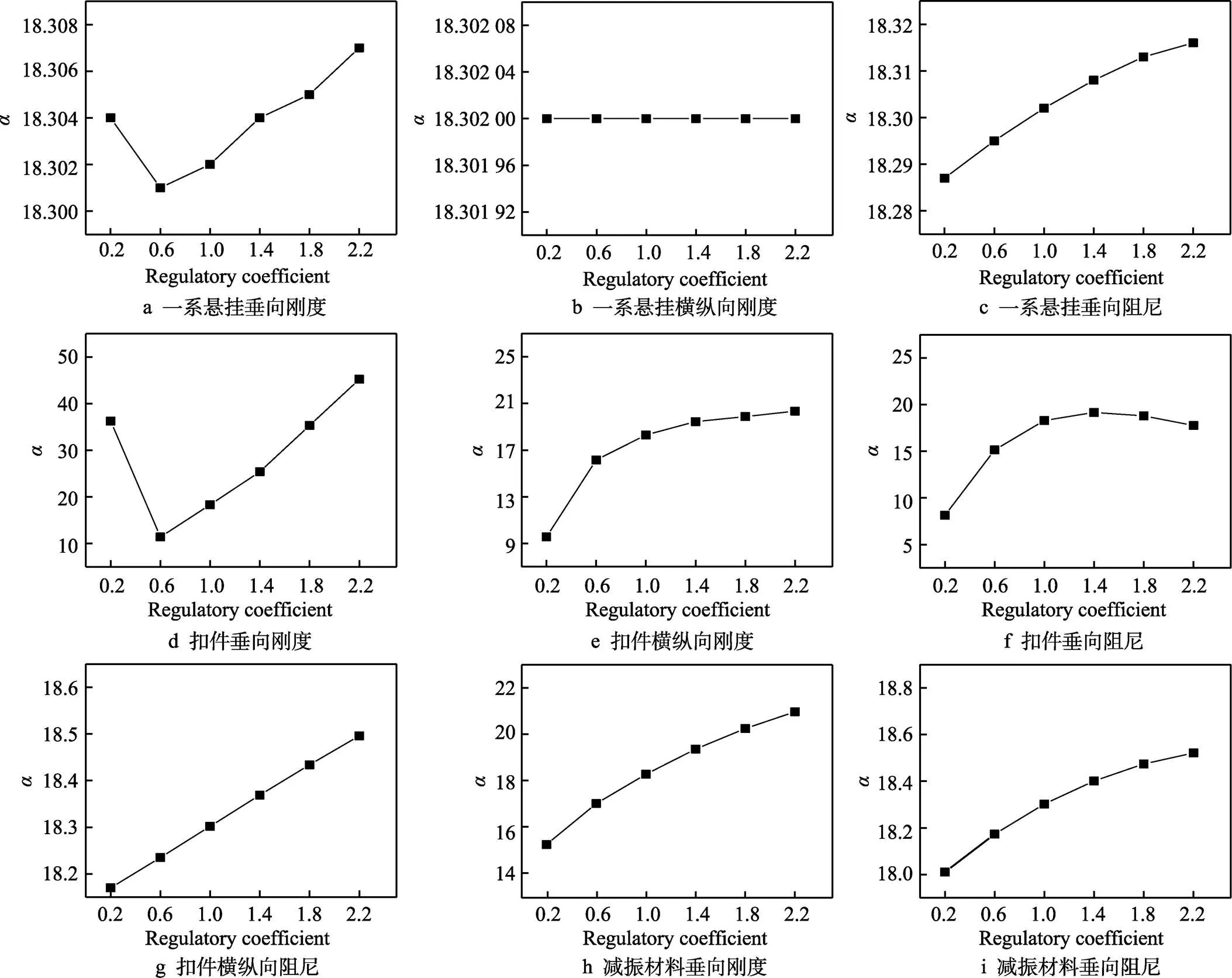
图5 单种参数对摩擦自激振动的影响

此外，通过以上参数分析可发现，图5d中复特征值实部的变化范围最大，为10～45；图5e、f、h中，复特征值区间相对较大，复特征值实部的变化范围分别为9～21、8～21、15～21。由此可以认为，影响不稳定振动的关键因素为轨道结构中扣件的垂向刚度、横纵向刚度、垂向阻尼和减振材料的垂向刚度。通过参数化分析发现，轨道结构参数对不稳定振动的影响更明显，通过改善上述4种轨道结构参数，更有利于有效抑制钢轨波磨。

2.3 梯形轨道结构的多参数拟合

通过控制变量法对梯形轨道上轮轨系统参数的分析结果，可以得出每种单一参数对不稳定振动的影响程度与影响规律。为进一步研究轨道结构显著参数之间的相互关系对不稳定振动的影响，需对轨道结构中影响不稳定振动的关键参数进行拟合。

采用最小二乘法进行拟合，考虑4个关键参数之间的相互关系，构建多参数影响下对复特征值实部的预测。多参数拟合方程具体如公式(5)—(10)所示。

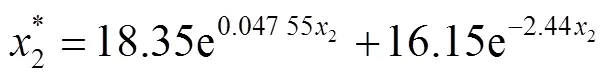
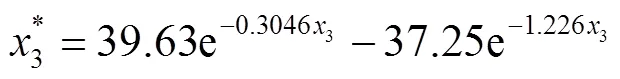
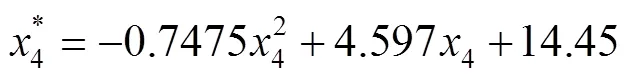
式中：x1、x2、x3、x4分别为扣件的垂向刚度、横纵向刚度、垂向阻尼和减振材料的垂向刚度4种因素的对应调整系数；x*1、x*2、x*3、x*4分别为x1、x2、x3、x4经一元非线性拟合后获得的参考值，其一元拟合方程为(6)—(9)，βb为多元拟合方程中16项多项式的每项系数，该组值经最小二乘法计算求解可得。摩擦自激振动的多元拟合方程误差分析如图6所示。该多元回归方程的均方根误差为0.8644，表明该方程拟合情况良好。

2.4 梯形轨道结构的多参数优化与验证

根据轨道结构的多参数拟合公式，对扣件的垂向刚度、横纵向刚度、垂向阻尼和减振材料的垂向刚度4种关键参数进行最优匹配，控制轮轨系统的复特征值实部，从而有效抑制轮轨系统摩擦自激振动的发生。考虑到该拟合方程的优化为多变量、非线性、难微分和多峰值的复杂优化问题，选取遗传算法[5-6,25]对上述4种显著参数进行局部优化匹配。

为实现上述优化方法，以求解复特征值实部最小时数组[1，2，x，4]的取值。根据参数化分析范围，设置数组中每种元素的取值区间为0.2～2.2，取值精度为0.01，初始种群为随机生成的给定数目个数组。经多次迭代计算，可稳定获得局部最优解为[0.90, 0.21, 0.29, 0.23]，即扣件垂向刚度为36 MN/m，扣件横纵向刚度1.68 MN/m，扣件垂向阻尼为2.9 kNs/m，减振材料垂向刚度为5.57 MN/m。

为验证遗传算法的优化结果，通过已建立的有限元模型，对优化结果进行复特征值分析，结果如图7所示。优化后模型的复特征值实部为6.2，相较于优化前的18.3，复特征值实部明显减小，进而说明优化结果能减小轮轨间摩擦自激振动发生的可能性，故可认为该组参数优化结果良好。

图7 优化结果验证

3 结论

为抑制梯形轨道小半径曲线路段上发生的钢轨波磨问题，本文基于轮轨耦合系统间的摩擦自激振动导致钢轨波磨的观点，进行了该种轨道上的多参数分析，并通过最小二乘法对主要参数进行拟合，以获得预测轮轨间不稳定振动发生可能性的多参数拟合方程。通过遗传算法对上述拟合方程进行求解，即对结构参数进行优化，提出了抑制梯形轨道小半径路段上钢轨波磨发生的措施。综上研究，得出如下结论：

1）诱导梯形轨道小半径曲线路段上钢轨波磨发生的主要因素为轮轨间饱和蠕滑力引起的不稳定振动，故抑制该路段上钢轨波磨可通过抑制轮轨间摩擦自激振动发生实现。

2）通过参数分析一系悬挂刚度阻尼、扣件刚度阻尼、减振材料刚度阻尼对波磨发生的影响，其中扣件垂向刚度、横纵向刚度、垂向阻尼与减振材料垂向阻尼的影响较为明显。

3）通过最小二乘法拟合与遗传算法求解，提出了优化方案，即当扣件垂向刚度为36 MN/m、扣件横纵向刚度1.68 MN/m、扣件垂向阻尼为2.9 kNs/m、减振材料垂向刚度为5.57 MN/m时，可有效地抑制小半径曲线梯形轨道低轨上的摩擦自激振动，从而有助于抑制对应频段下钢轨短波波磨发生的可能。

[1] WU Bo-wen, CHEN Guang-xiong, LV Jin-zhuang, et al. Generation Mechanism and Remedy Method of Rail Cor­ru­gation at a Sharp Curved Metro Track with Vanguard Fasteners[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2020, 39(2): 368-381.

[2] 陈光雄, 钱韦吉, 莫继良, 等. 轮轨摩擦自激振动引起小半径曲线钢轨波磨的瞬态动力学[J]. 机械工程学报, 2014, 50(9): 71-76.

CHEN Guang-xiong, QIAN Wei-ji, MO Ji-liang, et al. A Transient Dynamics Study on Wear-Type Rail Corruga­tion on a Tight Curve Due to the Friction-induced Self-ex­cited Vibration of a Wheelset-Track System[J]. Journal of Mechanical Engineering, 2014, 50(9): 71-76.

[3] GRASSIE S L. Rail Irregularities, Corrugation and Acou­s­tic Roughness: Characteristics, Significance and Effects of Reprofiling[J]. Journal of Rail and Rapid Transit, 2012, 226(5): 542-557.

[4] GRASSIE S L, KALOUSEK J. Rail Corrugation: Charac­teristics, Causes and Treatments[J]. Journal of Rail and Rapid Transit, 1993, 207(1): 57-68.

[5] YAN Zi-quan, MARKINE V, GU Ai-jun, et al. Optimi­sation of the Dynamic Properties of Ladder Track to Mi­nimise the Chance of Rail Corrugation[J]. Journal of Rail and Rapid Transit, 2014, 228(3): 285-297.

[6] YAN Zi-quan, MARKINE V, GU Ai-jun, et al. Optimi­zation of the Dynamic Properties of the Ladder Track Sys­tem to Control Rail Vibration Using the Multipoint Approximation Method[J]. Journal of Vibration and Con­trol, 2014, 20(13): 1967-1984.

[7] XIAO Hong, YANG Song, WANG Hao-yu, et al. Initia­tion and Development of Rail Corrugation Based on Track Vibration in Metro Systems[J]. Journal of Rail and Rapid Transit, 2018, 232(9): 2228-2243.

[8] LEI Zhen-yu, WANG Zhi-qiang. Generation Mechanism and Development Characteristics of Rail Corrugation of Cologne Egg Fastener Track in Metro[J]. KSCE Journal of Civil Engineering, 2020, 24(6): 1763-1774.

[9] WANG Zhi-qiang, LEI Zhen-yu, ZHAO Yang, et al. Rail Corrugation Characteristics of Cologne Egg Fastener Sec­tion in Small Radius Curve[J]. Shock and Vibration, 2020, 2020: 1827053.

[10] OYARZABAL O, GÓMEZ J, SANTAMARÍA J, et al. Dynamic Optimization of Track Components to Minimize Rail Corrugation[J]. Journal of Sound and Vibration, 2009, 319(3-5): 904-917.

[11] OYARZABAL O, CORREA N, VADILLO E G, et al. Modelling Rail Corrugation with Specific-Track Para­meters Focusing on Ballasted Track and Slab Track[J]. Vehicle System Dynamics, 2011, 49(11): 1733-1748.

[12] 刘春阳, 赵晓男, 陈光雄, 等. 一系悬挂与扣件参数对钢轨波磨的影响分析[J]. 机械, 2018, 45(10): 11-15, 19.

LIU Chun-yang, ZHAO Xiao-nan, CHEN Guang-xiong, et al. Influence of Primary Suspension and Rail Fastener Parameters on Rail Corrugation[J]. Machinery, 2018, 45(10): 11-15, 19.

[13] 于淼, 王卫东, 刘金朝. 钢轨波磨区段高速轮轨瞬态滚动接触高频动态特性[J]. 中国铁道科学, 2018, 39(5): 58-66.

YU Miao, WANG Wei-dong, LIU Jin-zhao. High Fre­quency Dynamic Characteristics of High-Speed Wheel- Rail Transient Rolling Contact in Rail Corrugation Sec­tion[J]. China Railway Science, 2018, 39(5): 58-66.

[14] 张珍珍. 梯形轨枕轨道力学性能分析[J]. 铁道勘测与设计, 2010(6): 34-37, 50.

Zhang Zhen-zhen. Analysis of Mechanical Properties of Ladder Sleeper Track[J]. Railway Survey and Design, 2010(6): 34-37, 50.

[15] 苏宇, 刘维宁, 孙晓静, 等. 梯形轨道减振性能研究[J]. 铁道标准设计, 2007, 51(10): 71-74.

SU Yu, LIU Wei-ning, SUN Xiao-jing, et al. Research on Vibration Reduction Performance of Ladder Track[J]. Railway Standard Design, 2007, 51(10): 71-74.

[16] 张杰, 姜坚白, 邓玉姝, 等. 浮置式梯形轨道的承载性能与环境性能分析[J]. 铁道标准设计, 2007, 51(10): 51- 54.

ZHANG Jie, JIANG Jian-bai, DENG Yu-shu, et al. Analysis of Bearing Capacity and Environmental Perfor­mance of Floating Trapezoidal Track[J]. Railway Stand­ard Design, 2007, 51(10): 51-54.

[17] 周素霞, 薛蕊, 张骞, 等. 地铁线路曲线段磨耗状态下轮轨滚动接触有限元分析[J]. 机械工程学报, 2016, 52(12): 129-135.

ZHOU Su-xia, XUE Rui, ZHANG Qian, et al. Wheel-Rail Rolling Contact Finite Element Analysis of the Wear State on the Curve of Subway Line[J]. Journal of Mechanical Engineering, 2016, 52(12): 129-135.

[18] 周信, 赵鑫, 韩健, 等. 波磨条件下地铁车轮瞬态滚动噪声特性研究[J]. 机械工程学报, 2018, 54(4): 196-202.

ZHOU Xin, ZHAO Xin, HAN Jian, et al. Study on Tran­sient Rolling Noise Characteristics of Subway Wheel with Rail Corrugation[J]. Journal of Mechanical Engineering, 2018, 54(4): 196-202.

[19] QIAN W J, CHEN G X, OUYANG H, et al. A Transient Dynamic Study of the Self-excited Vibration of a Railway Wheel Set-track System Induced by Saturated Creep Forces[J]. Vehicle System Dynamics, 2014, 52(9): 1115- 1138.

[20] CHEN G X, ZHOU Z R, OUYANG H, et al. A Finite Element Study on Rail Corrugation Based on Saturated Creep Force-induced Self-Excited Vibration of a Whee­lset-Track System[J]. Journal of Sound and Vibration, 2010, 329(22): 4643-4655.

[21] ABUBAKAR A R, OUYANG Hua-jiang. Complex Ei­genvalue Analysis and Dynamic Transient Analysis in Predicting Disc Brake Squeal[J]. International Journal of Vehicle Noise and Vibration, 2006, 2(2): 143.

[22] 夏晨光, 陈光雄, 朱旻昊, 等. 车轮辐板阻尼涂层对钢轨波磨的影响[J]. 表面技术, 2020, 49(3): 134-140.

XIA Chen-guang, CHEN Guang-xiong, ZHU Min-hao, et al. Effect of Damped Coating of Wheel Web on Rail Corrugation[J]. Surface Technology, 2020, 49(3): 134- 140.

[23] 赵晓男, 陈光雄, 崔晓璐, 等. 高速列车车轮多边形磨耗的形成机理及影响因素探究[J]. 表面技术, 2018, 47(8): 8-13.

ZHAO Xiao-nan, CHEN Guang-xiong, CUI Xiao-lu, et al. Formation Mechanism and Influencing Factors of the Polygonal Wear of High-speed Train Wheels[J]. Surface Technology, 2018, 47(8): 8-13.

[24] 崔晓璐, 黄博, 陈光雄. 抑制轮轨摩擦自激振动的扣件结构多参数拟合研究[J]. 西南交通大学学报, 2021, 56(1): 68-74.

CUI Xiao-lu, HUANG Bo, CHEN Guang-xiong. Re­search on Multi-Parameter Fitting of Fastener Structures to Suppress Wheel-Rail Friction Self-excited Vibration[J]. Journal of Southwest Jiaotong University, 2021, 56(1): 68-74.

[25] PERSSON I, IWNICKI S. Optimisation of Railway Wheel Profiles Using a Genetic Algorithm[J]. Vehicle Sy­stem Dynamics, 2004, 41: 517-526.

Multi-parameter Fitting and Optimization of the Ladder Track to Minimize Rail Corrugation

1,1,2

(1. School of Mechanotronics and Vehicle Engineering, Chongqing Jiaotong University, Chongqing 400074, China; 2. Chongqing Rail Transit (Group) Co., Ltd., Chongqing 401120, China)

The work aims to study the influence of the primary suspension of the metro vehicle structures and support stiffness and damping of the track structures about the rail corrugation on the ladder track in the sharp curve, and to put forward the multi-parameter fitting and optimizing methods of minimizing the rail corrugation on the ladder track in the sharp curve at the corresponding section. A corresponding finite element model of the wheelsets-rail system with primary suspension on the ladder track in the sharp curve was constructed based on the theory of frictional self-excited vibration in the wheel-rail system. The characteristics that frictional self-excited vibration of the wheel-rail system occurred on the ladder track in the metro’s sharp curve section was analyzed according to the complex eigenvalue analysis. Based on the finite element model, the parametric analysis was developed about the primary suspension of vehicle structures and support stiffness and damping of track structure. The multi-parameter fitting was carried out about crucial parameters for affecting the unstable vibration by adopting the least square method. In accordance with the fitting equation, the genetic algorithm was adopted for optimization of the crucial parameters. The results show that, on the ladder track with curve radius of 350 m, the frictional self-excited vibration is caused by the saturated creep force between wheel and rail. The unstable vibration occurs at the frequency of 439.02 Hz, which leads to the rail corrugation. The four groups of parameters which have crucial influence are vertical stiffness of fasteners, transverse and longitudinal stiffness of fasteners, vertical damping of fasteners, vertical stiffness of damping materials. When the vertical stiffness of the fastener is 36 MN/m, the transverse and longitudinal stiffness of the fastener is 1.68 MN/m, the vertical damping of the fastener is 2.9 kNs/m, and the vertical stiffness of the damping material is 5.57 MN/m, the possibility of rail corrugation can be effectively suppressed.

rail corrugation; ladder track; frictional self-excited vibration; complex eigenvalue analysis; multi-parameter fitting; genetic algorithm

U260

A

1001-3660(2022)02-0185-08

10.16490/j.cnki.issn.1001-3660.2022.02.017

2021-03-24；

2021-07-12

2021-03-24；

2021-07-12

国家自然科学基金项目（51805057）；中国博士后科学基金项目（2019M663889XB）；重庆市基础研究与前沿探索项目（cstc2018jcyjAX0636）；重庆市教委科学技术研究项目（KJQN201900734）

The National Natural Science Foundation of China (51805057), the National Science Foundation for Post-doctoral Scientists of China (2019M663889XB), the Basic Natural Science and Frontier Technology Research Program of Chongqing Municipal Science Foundation (cstc2018jcyjAX0636) and the Science and Technology Research Program of Chongqing Municipal Education Commission (KJQN201900734)

崔晓璐（1990—），女，博士，副教授，主要研究方向为轮轨摩擦学。

CUI Xiao-lu (1990—), Female, Doctor, Associate professor, Research focus: wheel-rail tribology.

崔晓璐, 李童, 漆伟. 抑制钢轨波磨的梯形轨道结构的多参数拟合与优化[J]. 表面技术, 2022, 51(2): 185-192.

CUI Xiao-lu, LI Tong, QI Wei. Multi-parameter Fitting and Optimization of the Ladder Track to Minimize Rail Corrugation[J]. Surface Technology, 2022, 51(2): 185-192.