基于StatRF 基波正序提取方法的三相四开关HAPF

柴杰彤，刘洪臣

（哈尔滨工业大学电气工程及自动化学院，哈尔滨 150000）

0 引言

为了降低有源滤波器的成本，推广有源滤波技术的应用，许多学者提出了形式多样的有源电力滤波器（active power filter，APF）与无源滤波器结合的混合型滤波器（hybrid active power filter，HAPF），取得了良好的经济效益和滤波效果[1-9]。四开关逆变器与六开关逆变器相比少了一对开关器件，整个装置的驱动电路和散热装置均更加简单，对发展经济型逆变器有重要的意义。电机驱动领域的四开关逆变控制技术发展较早，由于近年来新能源发电技术的大量应用，致使电网电能质量问题日益突出，四开关APF 逐渐得到了学者的关注[10-14]。

在已有文献中，四开关APF 相关研究主要涉及直流侧电容均压控制、三相电压不平衡条件下电流控制和故障容错策略等。传统三相四开关APF 的C 相采用分裂电容结构，电容桥臂上流过交流电流，引起直流母线中点电位的偏移，导致APF 输出电流失衡，所以有很多文献通过电容均压控制的方法进行解决[10-11]。针对电网电压跌落引起的不平衡和短时故障等现象，从补偿目标出发，在矢量分析的基础上，文献[12]提出了一种基于线电压合成的电流参考值生成策略。作为六开关APF 的容错运行拓扑，有许多文献通过三相四开关容错型APF 及其容错切换策略进行解决[13-14]。

本文将传统四开关APF 的有源部分和无源滤波器（power filter，PF）结合，提出一种新型三相四开关混合型滤波器（HAPF）。直流侧电压控制和谐波检测环节均基于StatRF 的基波正序电流提取方法[15-17]。这种检测方法免去了繁复的坐标变换，计算更加简单，并且无需锁相环。最后通过仿真和实验验证了所提方法的正确性。

1 三相四开关HAPF系统

1.1 三相四开关HAPF拓扑

传统三线制APF 拓扑见图1（a），采用三相全桥结构，需要6 个开关器件，采用单个电感滤除开关频率的谐波。无变压器HAPF 拓扑见图1（b），采用LC 滤波器代替单电感滤波，其可以滤除开关谐波，增强某低次谐波的滤波效果，滤波电容承担大部分基波电压，开关器件承受的电压得到降低进而降低了有源部分的容量[8-12]。

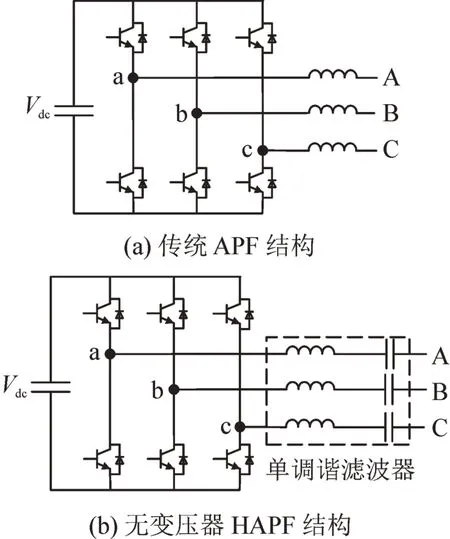
图1 传统APF结构及无变压器HAPF结构Fig.1 Traditional APF structure and HAPF structure without transformer

为进一步降低APF 中开关器件成本，提出了三相四开关HAPF 拓扑结构，见图2。图2 中混合滤波器由有源逆变和LC 滤波器组两部分构成。有源逆变部分由4 个开关管组成两个桥臂，分别通过各自LC 滤波器并联接入电网A、B 相的公共耦合点。两组LC 滤波器并联在电网C 相和直流母线负极两端。C 相滤波器组可根据负载的要求配置，在本文中由5 次和7 次调谐滤波器并联构成。相较于传统无变压器型HAPF，在三线制系统中实现有源滤波只需要4 个开关管。

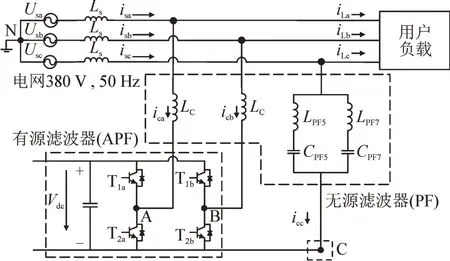
图2 三相四开关APF拓扑Fig.2 Topology of three⁃phase four switch APF

1.2 三相四开关HAPF原理分析

以电感电流和电容电压为状态变量，列写APF中三相四开关逆变器的数学模型。在图2 中，由基尔霍夫电压定律可得公式

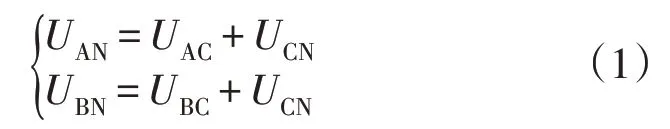
对于平衡的三相系统有

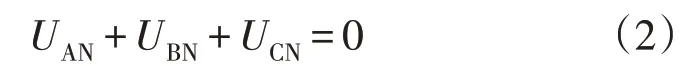
将式（2）代入式（1）可得公式为

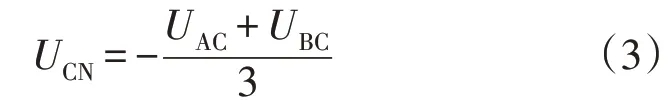
式中电压UAC、UBC满足公式为

式中:Vdc为直流侧电压；Sa/b为开关函数，公式为

根据基尔霍夫电压定律，电压回路方程为

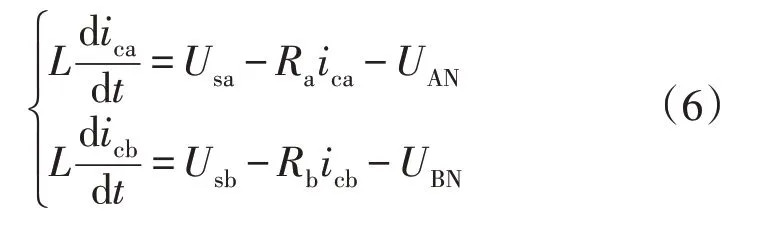
式中，Ra/b为电感Lc的等效电阻。

将式（1）、式（3）-（4）代入式（6）可得公式

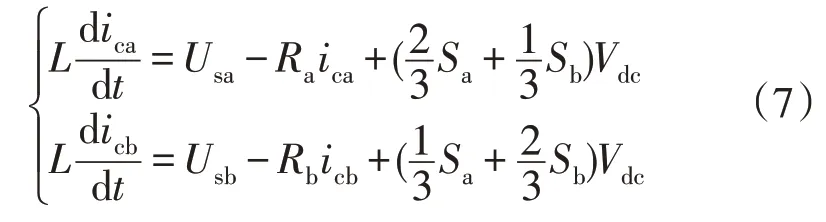
由式（7）可知，在Vdc保持恒定的情况下，采用脉宽调制（pulse width modulation，PWM）方法，通过控制功率器件的通断，即改变触发信号Sa和Sb，即可实现对A 相、B 相电流的控制，并进一步控制C 相电流。

2 无源滤波器参数设计

LC 滤波器设计关系到APF 的整体滤波特性，各参数需从多个角度综合考虑。需要考虑的因素有：谐振频率、品质因数、额定电压和无功容量。以下分别进行讨论

1）LC 滤波器的谐振频率见式（8），ωr应选在待补偿谐波的主要频次，这样PF 即可对谐波有较好的滤除效果。

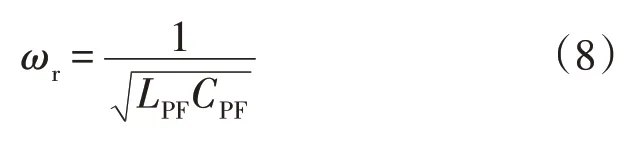
2）LC 滤波器的品质因数见式（9），为了在ωr附近获得较低的阻抗，QPF应适当选较小值，30＜QPF＜100，因为RPF关系到滤波器损耗，所以应尽量减小LPF/CPF值。

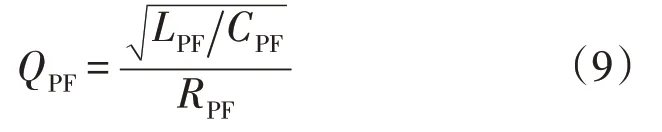
3）讨论LC 滤波器的耐压，按照电路的叠加定理，分为直流和交流两种情况考虑。在这两种情况中，电抗均忽略不计，因此主要讨论电容的耐压。考虑直流电压时，令电网电压vs=0，

考虑交流电压时，令直流电压Vdc=0，

式中，VPCC为公共连接点（point of common coupling，PCC）线电压，所以电容电压vPF应当满足公式为

4）三相LC 滤波器的无功补偿容量近似于式（13），式中ω1为基波角频率。

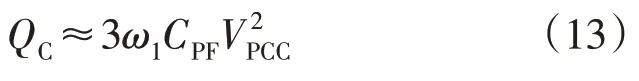
3 有源滤波器的控制策略与控制方法

3.1 电流跟踪控制策略

随着控制理论的发展以及对APF 研究的深入，APF 电流跟踪控制策略中引入了许多自动控制、智能控制理论。目前应用最多、最成熟的理论仍旧是经典的PI 控制。PI 控制器理论上能够对直流信号进行无漂移跟踪，算法简单，易于实现，动态性能好，鲁棒性强，见图3。但对于有源电力滤波器来说，其被控信号中存在大量无功和高次谐波分量，PI 控制器对这些高频分量不能实现无静差跟踪，所以采取了PI 控制与重复控制联合的复合控制策略。

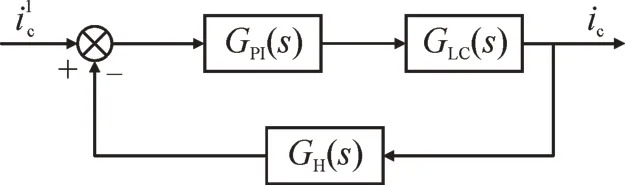
图3 采用PI控制器等效图Fig.3 Equivalent diagram using PI controller

图中：为谐波一次电流；GPI(s)为PI 控制器；GLC(s)为LC 滤波器；GH(s)为抗混叠滤波器。

3.2 控制方法

3.2.1 StatRF 基波提取方法

旋转参考坐标法（synchronous reference frame，SRF）是提取基波正序提取的常用方法，三相电流经过Park 坐标变换，将其从三相静止坐标系转换到两相旋转坐标系。在dq 坐标系中，基波正序分量为直流量，可通过低通滤波器得到，之后再经过坐标反变换得到abc 坐标系下的基波正序量。一阶LPF的传递函数为

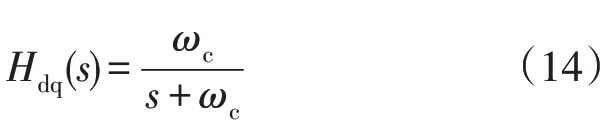
式中，ωc为一阶LPF 的截止频率。上述SRF 方法滤波效果较好，但其存在多次坐标变换和PLL 环节，计算复杂。在四开关HAPF 中，只需要用到A、B 两相即可，因此可采用形式更为简单的静止坐标StatRF 控制方法。StatRF 与SRF 的关系见图4。

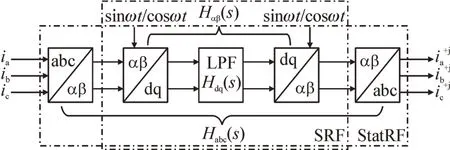
图4 StatRF与SRF的关系Fig.4 Relationship between the SRF and StatRF

将LPF 从dq 坐标系转换到αβ坐标系。αβ坐标系下的变换矩阵为

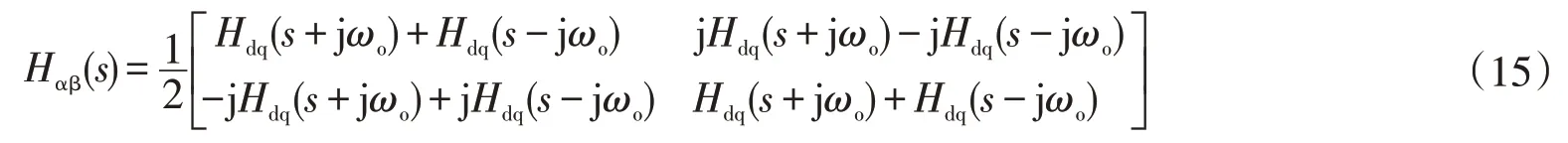
式中，ωo为所待提取的基波频率。将LPF 传递函数式（14）代入式（15），再经过abc/αβ变换，得到abc坐标下等效一阶LPF 传递函数矩阵公式为

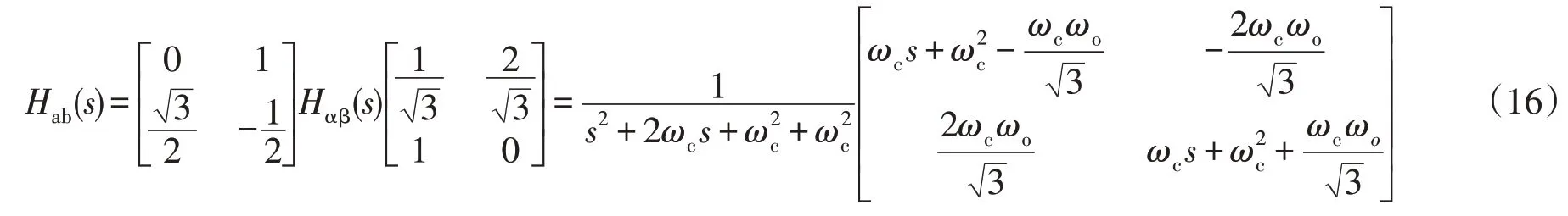
式（16）即SRF 在静止坐标系下的等效方法。畸变电流经过式（16）计算，可得到基波正序电流、。本文设计LPF 的ωc取62.8 rad/s。对于三相三线系统，可由KCL 计算，本文设计的四开关HAPF 则不需要计算。

3.2.2 直流侧电压控制方法

计量资料数据分析结果以（±s）表示，两组间均数比较采用t检验和秩和检验，计数资料采用χ2检验，以P＜0.05为差异有统计学意义。所有数据均采用SPSS23.0软件进行统计学处理。

采用传统SRF 控制方法的APF，其直流侧电压是通过将电压调节量u*作为d轴给定电流idref，而采用StatRF 基波正序提取法，电流内环不存在dq 坐标。基于StatRF 基波正序提取的电压电流双闭环见图5。电压调节量u*与基波正序分量isaf、isbf相乘，产生电压调节信号iua、iub。谐波电流isah、isbh，基波电流isaf、isbf和电压调节信号iua、iub经电流综合之后，经过电流调节器Ks，然后经过PWM 调制，产生开关管驱动信号。

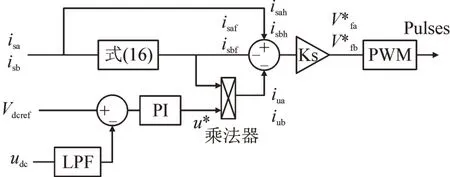
图5 基于StatRF基波正序提取的电压电流双闭环Fig.5 Voltage and current double closed loop based on StatRF fundamental wave positive sequence extraction

4 仿真与实验分析

为了验证HAPF 结构和控制方法的可行性，在Matlab/Simulink 软件中搭建了相应的仿真模型。用户负载为交流侧带平波电抗器Lac，直流侧带电阻Rload的三相不控整流桥。具体仿真参数见表1。

表1 仿真参数Table 1 Simulation parameters

能否准确提取基波电流关系到生成谐波参考电流的准确度，是影响APF 性能的重要因素。图6 是采用StatRF 方法提取基波正序电流的仿真波形。图中分别给出了A 相负载电流iLa及其分解的基波正序电流、isaf、谐波电流isah。经过仿真分析，所提取的isaf的THD 约0.6%，形状十分接近正弦波。

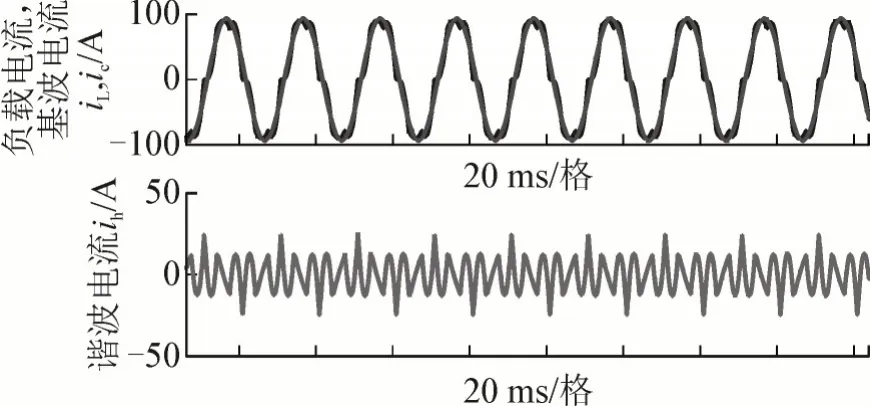
图6 StatRF基波正序提取Fig.6 StatRF fundamental waves positive sequence extraction

图7 和图8 分别为混合滤波器进入稳态运行时的波形图和FFT 图，补偿前后主要频次谐波含量见表2。负载电流iL的THD 为14.7%，经过滤波以后，A、B 两相电源电流isa、isb的THD 分别降低到3.7%、3.4%。C 相电源电流isc的THD 为4.8%，略高于A、B 两相，能够满足IEEE-519 标准。

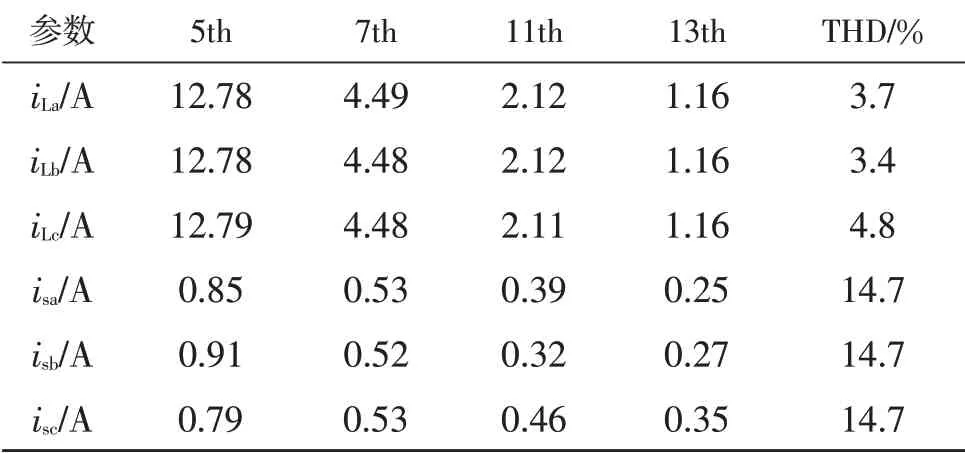
表2 主要频次谐波含量Table 2 Harmonic content of main frequency

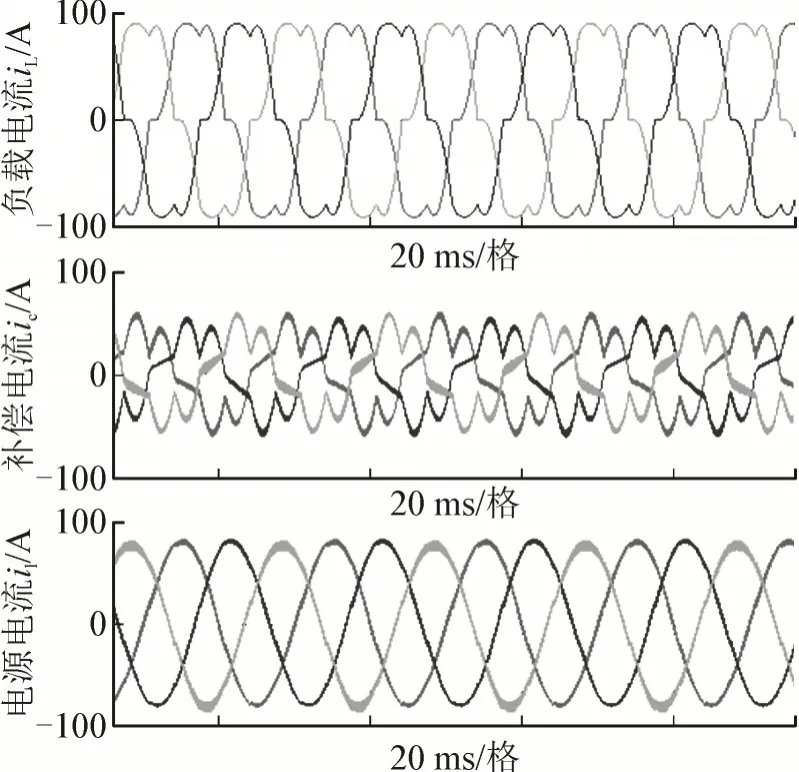
图7 三相四开关HAPF稳态波形Fig.7 Steady waveform of three⁃phase four⁃switch HAPF

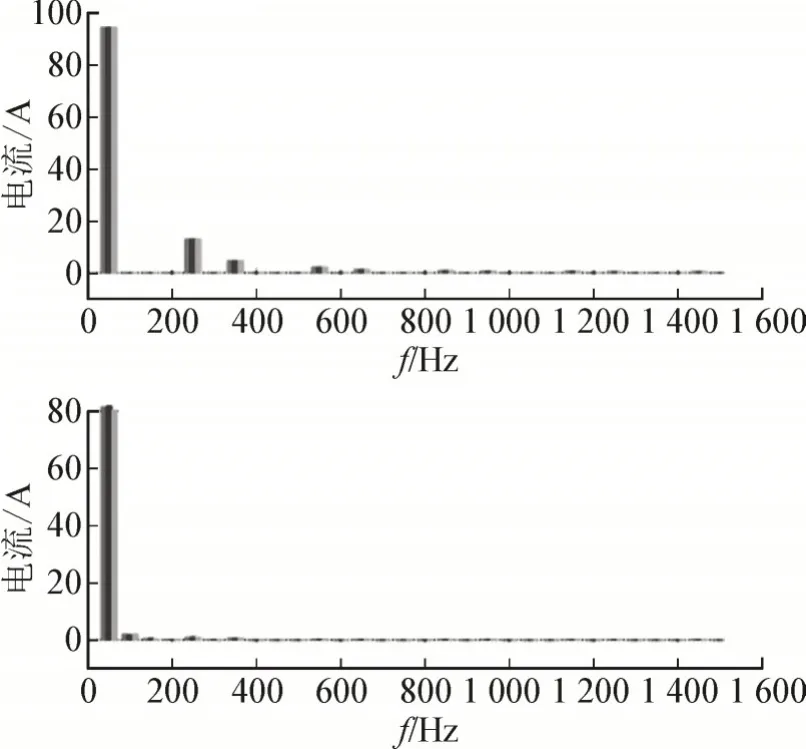
图8 三相四开关HAPF稳态FFTFig.8 Steady FFT of three⁃phase four⁃switch HAPF

图9 是HAPF 从启动运行，直流侧升压到负载突增突减整个过程中的动态响应波形，图10 为其实验波形。0.5 s 时启动运行，经过大约0.2 s 后直流侧电压上升到800 V，充电完成。1.0 s 时负载突增，1.4 s 时负载突减，从右侧放大图中可以看出，电源电流在1 个基波周期内即可调节到正弦波，动态响应较好。

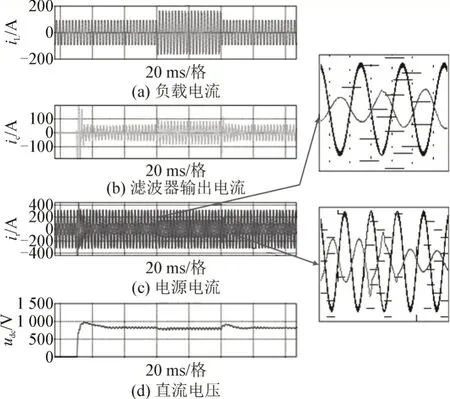
图9 动态响应波形Fig.9 Dynamic response waveform

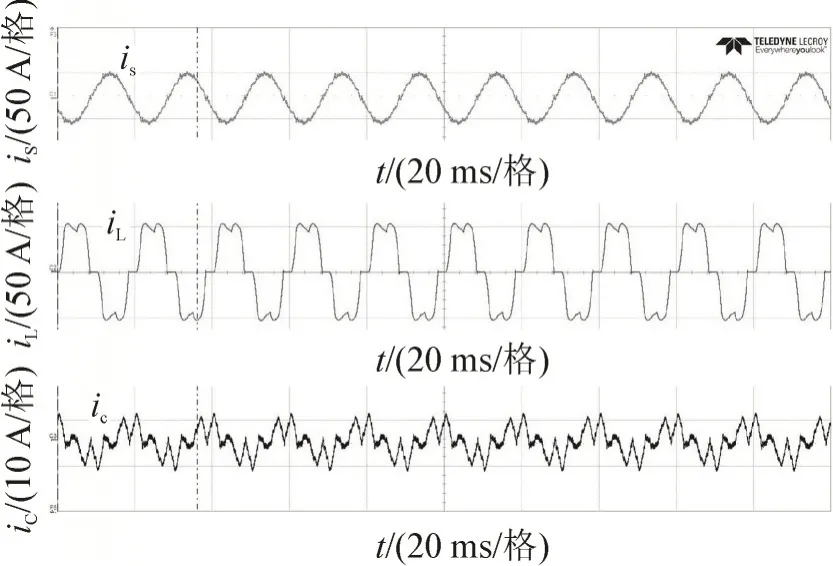
图10 三相四开关HAPF实验波形Fig.10 Experimental waveform of the three⁃phase four⁃switch HAPF

5 结语

本文提出了一种适用于三相系统的四开关HAPF 及其控制方法，并且通过仿真和实验验证了其正确性。优势所在与传统全桥APF、无变压器型HAPF 相比，三相四开关HAPF 在硬件上具有开关器件少、功耗低、成本低的优点。在图4 中运用StatRF 方法经过abc/αβ变换，得到简单的公式，简化计算过程。本文采用静止坐标系StatRF 方法进行基波正序电流提取，这种方法避免了繁琐的坐标变换，简化了计算，更适用于三相四开关HAPF。