基于BP 神经网络建模的并联型有源电力滤波器谐波综合治理控制算法

左宏基，陈宏军，徐峰亮，刘煜，张云鹏，邹峰恩，程萌萌

（河南省电力公司信阳供电公司，河南 信阳 464000）

0 引言

随着现代工业社会的发展，能源问题逐渐成为亟待解决的世界级问题之一，而无论是何种能源，最终都需转化为电能，并且由于各类精密性产业的重要性日益凸显，电能质量问题也越来越受到学者们的关注，其中，谐波问题又是电能质量问题中的热点之一。目前，有源电力滤波器（active power filter，APF）以其可以对谐波及无功功率同时补偿、受电网影响较小及动态补偿的优点，广泛应用于谐波治理领域，然而，APF 的传统补偿方式仅限于单点谐波的治理，仍有一定的局限性。

对于含有多个分布式谐波源的局域电网来说，如采用就地补偿的方式优化电网整体的电能质量，需要大量APF 同时进行治理。这种方法并不经济，并且，如果仅有部分谐波源得到了治理，当安装位置和补偿负载选择不合理时，电网的整体电能质量并不能保证一定得到优化，严重时甚至会导致部分节点的电能质量比治理前恶化[1]。因此，如何利用少量APF 对包含许多分布式谐波源的局域电网的谐波进行系统级的综合优化治理是目前急需解决的问题。

针对这个问题，目前的研究方法可以分为两类，一是将该问题化为优化问题求解[2-6]，二是采用在线控制[7-15]。第1 种方法假设已知电网的结构、阻抗参数以及负载参数，目的在于求出系统谐波抑制的最优解，其中包括治理电流的幅值、相位以及治理设备最优安装点等。所采用的方法包括非线性优化法[2]、混合整数规划法[3]以及启发式算法[4-6]，这些方法本身能够给出具体的治理方案，但其精确度受制于模型精度，且计算量一般较大，难以应用实际的治理中。第2 种方法则对电网相关阻抗参数要求不高，但一般仍需指定特定网络结构[7-13]而在不需要特定网络结构的控制方法中，所采用的启发式算法[14]极值寻优算法[15]需要引入迭代计算，实时性较差。

基于以上原因，本文提出一种基于神经网络建模的谐波综合治理算法，该算法利用神经网络的函数逼近能力，通过对电网采样，基于数据训练神经网络，得到电网对补偿电流的反馈模型，并在此基础上计算最优综合补偿电流。由于采用了数据拟合的方式建模，对电网参数的要求不高，有利于其在实际工程中的应用。最后本文通过Matlab/Simulink 仿真，建立了电网及相关综合治理的模型，验证了所提方法的有效性。

1 APF传统控制方法及其局限性

1.1 单点谐波就地补偿原理

图1 所示为最基本的并联型有源电力滤波器（shunt active power filter，SAPF）系统构成的原理图。其基本工作原理是，检测补偿对象的电压和电流经指令电流运算电路计算得出补偿电流的指令信号，该信号经补偿电流发生电路放大，得出补偿电流，补偿电流与负载电流中要补偿的谐波及无功等电流抵消，最终得到期望的电源电流[16]。该工作方式被称为就地补偿，响应速度快，不易受电网影响，但仍有其局限性。

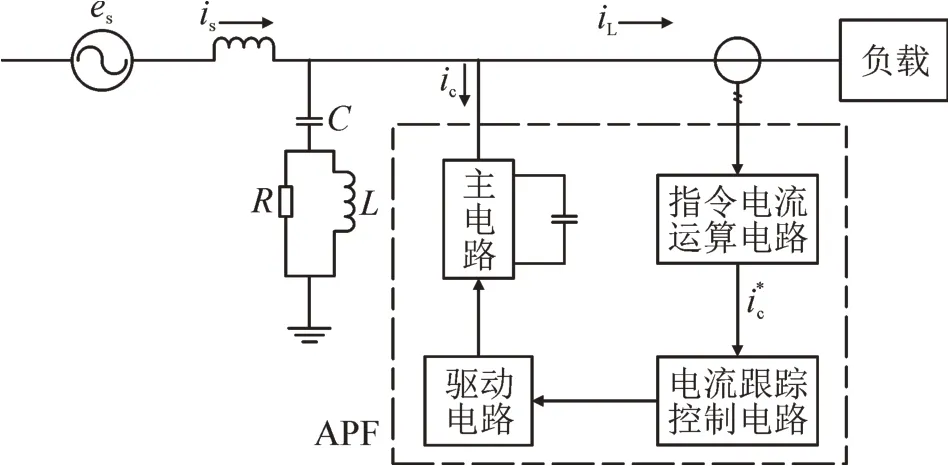
图1 并联型有源电力滤波器系统Fig.1 Shunt active power filter system

1.2 单点补偿的局限性

以三节点单相电路系统为例。图2 所示为一单相三节点系统，其中在节点2 和节点3 上各挂有一个非线性负载，节点3 上并联一SAPF，非线性负载和SAPF 都简化为电流源，便于分析[1]。

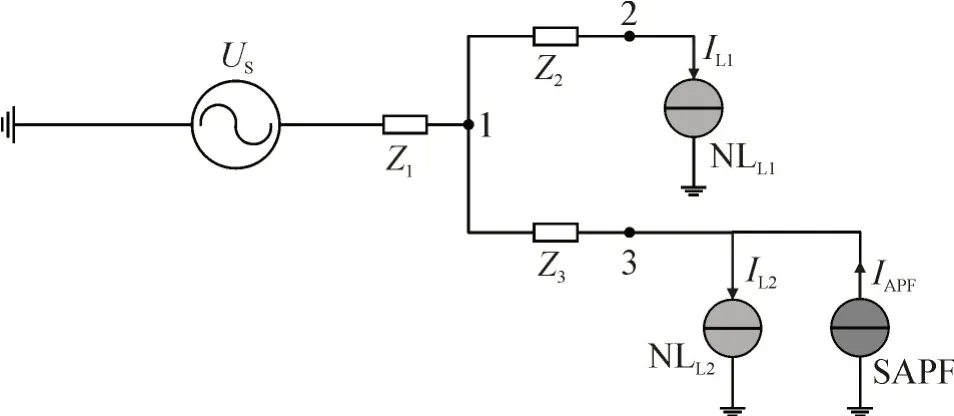
图2 含分布式谐波源的三节点系统Fig.2 Three⁃node system containing distributed harmonic sources

由图3 易知，3 个节点的谐波电压公式为

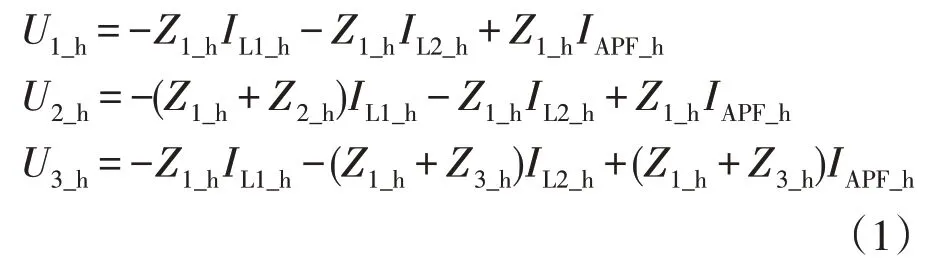
由式（1）可知，节点电压由3 个分量U1、U2、UAPF组成，3 个分量分别与NLL1、NLL2的电流和SAPF 的电流有关，且NLL2的分量U2可由SAPF 的分量UAPF完全抵消。假设SAPF 工作方式为就地补偿，则各点的谐波电压矢量图可见图3。

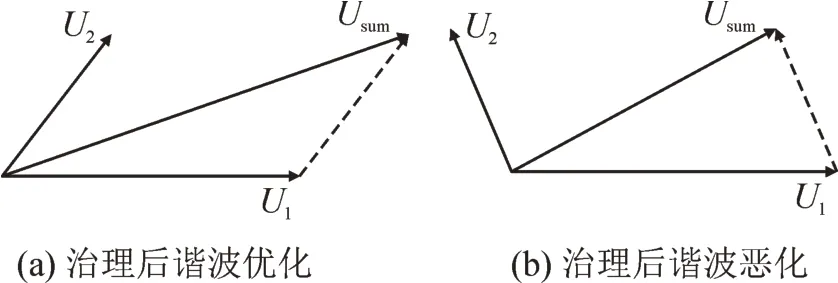
图3 各点谐波电压矢量图Fig.3 Vector diagram of harmonic voltage of each node

治理前，各节点谐波电压合矢量为Usum，治理后，U2被完全抵消，合矢量即为U1，若U1幅值大于Usum的幅值，即代表治理后谐波得到抑制，反之谐波则更为恶化。如图3（a）情况较好时，U1的幅值小于Usum，谐波受到抑制，当如图3（b），情况较坏时，U1的幅值将大于Usum，也就是说由于治理过程破坏了原本谐波之间的“平衡”，导致治理后的节点谐波电压反而更为恶化，这也说明了就地补偿的局限性。

2 BP神经网络原理及其建模求解

2.1 基于神经网络的电网黑箱建模原理

神经网络从构成上来说可以视为按照一定规则连接起来的神经元。图4 所示为一全连接5 层神经网络[17]。

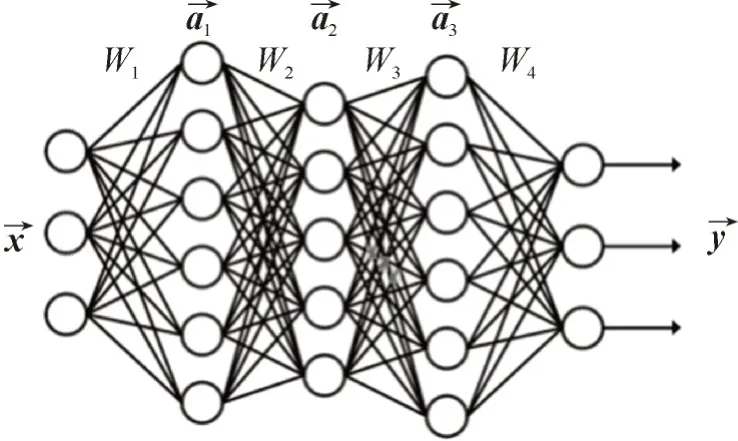
图4 全连接5层神经网络Fig.4 Fully connected 5⁃layer neural network

本文所采用的神经网络即是按照全连接方式连接的BP 神经网络。其规则为：

1）神经元按照层来布局。最左边的层为输入层，负责接收输入数据；最右边的层为输出层，其输出即为神经网络的输出。输入层和输出层之间的层为隐藏层，他们对于外部来说不可见。

2）同一层的神经元之间没有连接。

3）第N层的每个神经元和第N-1 层的所有神经元相连，第N-1 层神经元的输出即第N层神经元的输入。

4）每个连接都有一个权值。

如将全连接神经网络表示为函数，则可有如下定义，设n为层数，wnr为第n层第r个神经元的权重，bnr为该神经元偏置，均为矢量，G(•)为神经元激活函数。则第n层的输入输出关系公式为

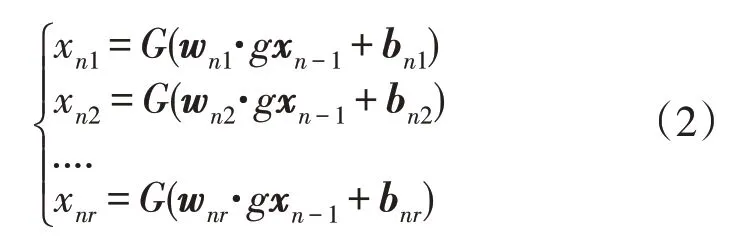
式中：xn-1为第n-1层输出矢量；g代表矢量点积。

将每层神经元视为一个函数，则xn公式为

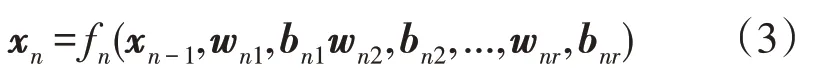
因此，n层全连接神经网络可由公式表示为

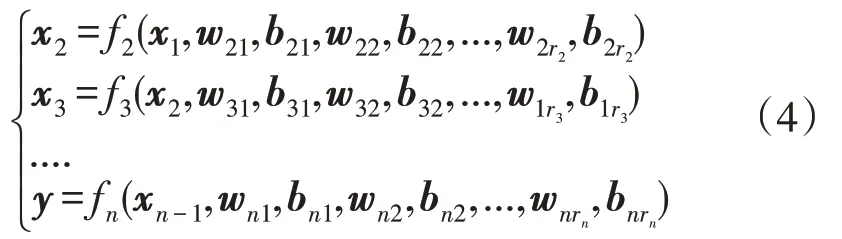
式中，y为神经网络最终输出矢量。可以证明，当n≥3 时，如隐藏层神经元个数无限制，则任意可测函数都可由该神经网络所表示的函数以任意精度逼近。因此，只需证明所需电网模型满足可测性即可证明神经网络建模的合理性。

假设有一个含有许多分散谐波源的m节点的三相电网，其中有n个谐波源负载（以及j个SAPF）。将这些谐波源负载和SAPF 用电流源代替，考虑网络中的其他参数，则电网各节点任意h次电压可以写为

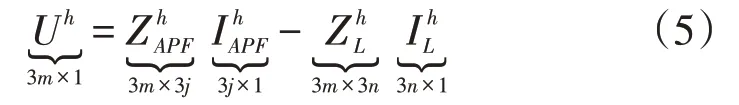
式中：Uh为SAPF 补偿后电网各节点的h次电压相量；和分别为SAPF 和谐波源负载的h次电流相量；和分别为从SAPF 电流和谐波源电流到各节点电压的转移阻抗。

不考虑电网中三相不平衡因素，易知各相电压与各SAPF 的补偿电流之间的关系可由一连续函数表示，而连续函数必为可测函数，因此全连接神经网络可用于SAPF 对电网综合治理的建模。

2.2 “补偿电流-节点电压”函数建模求解

相较于传统的建模方法，神经网络建模的优势在于对于相关参数的需求较少，本文中所建立的电网电压对补偿电流的反馈模型仅需知道特定补偿电流与各待治理节点电压之间的关系即可，因此，建模所采集数据需要令SAPF 在开始时向电网注入一定的扰动电流，以获取补偿电流-节点电压的数据对，数据格式见表1，其原理见图5。

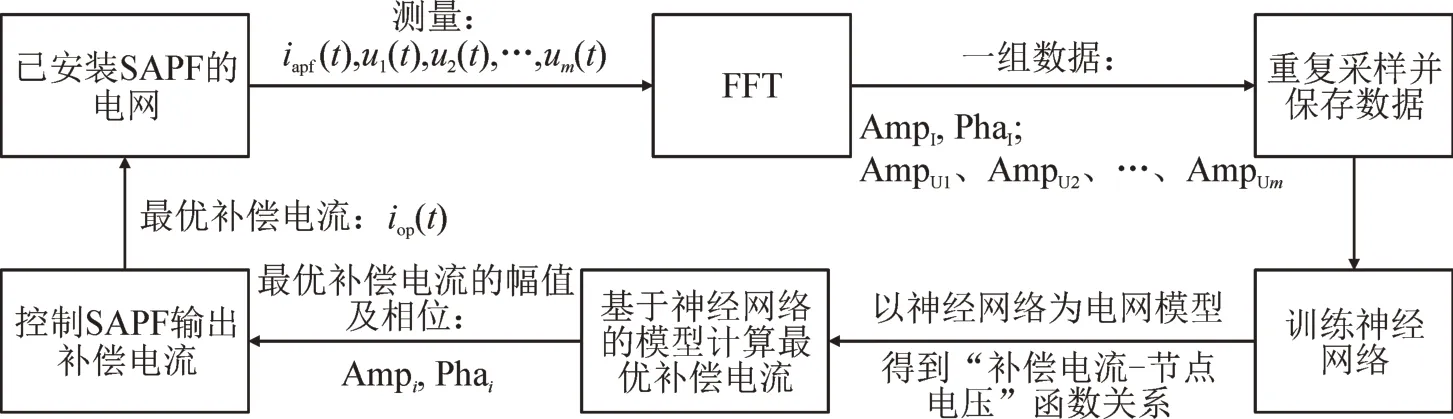
图5 神经网络建模流程图Fig.5 Flow chart for modeling of neural network

表1 训练所用数据的格式Table 1 Data format for training

其输入为补偿电流的幅值AmpI、相位PhaI，输出为各节点谐波电压的幅值AmpU1、AmpU2及AmpUm等。完成训练后，向神经网络输入补偿电流的幅值相位，即可输出各节点谐波电压幅值的预测值。

得到电网电压对补偿电流的反馈模型后，求使电网谐波含量最小的补偿电流过程可化为一优化问题。假设待治理节点有m个（m应小于等于全部节点数），第r个节点所需治理的各次谐波电压含量为，则该优化问题的目标函数可表示为

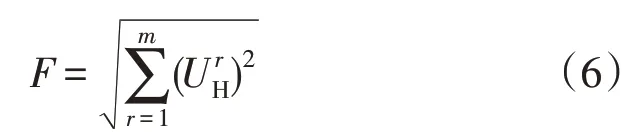
该目标函数可表示为补偿电流的函数，因此可根据建模所得模型求解使目标函数最小的补偿电流幅值及相位。值得注意的是，UrH为所需治理的谐波次电压有效值平方和的算术平方根，因此根据需要，可针对特定次谐波进行治理，比如只治理5、7次谐波，此时可表示为

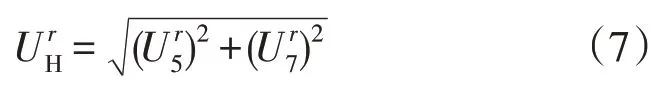
因此，建模时需对5、7 次谐波分别建模。由于神经网络模型的特殊性，求解方式一般采取梯度下降法等迭代算法，此处不再赘述。

3 仿真验证

3.1 仿真设计

本文通过Matlab/Simulink 仿真，在Simulink 中搭建了电路模型，并用Matlab 控制其采样、建模及治理，对基于神经网络建模的谐波综合治理算法进行了验证[18]，电路图见图6。

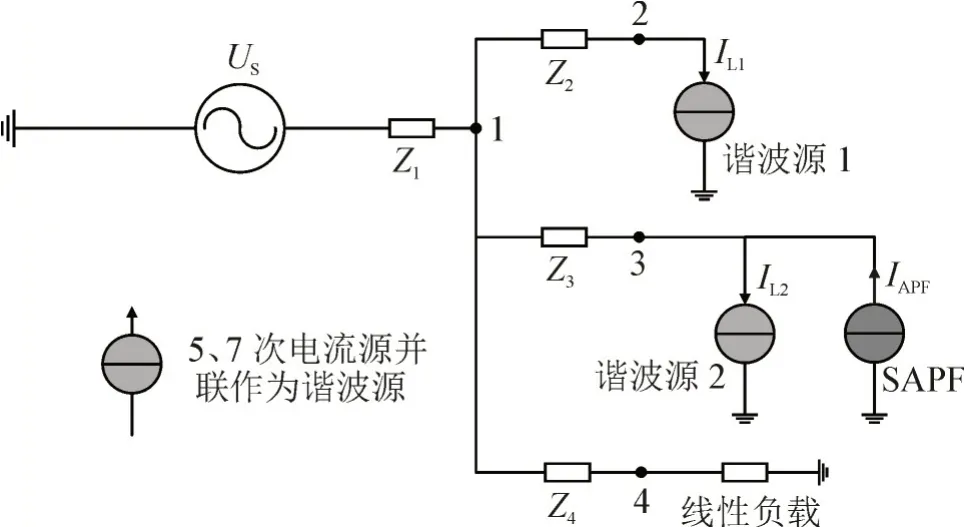
图6 待治理电路Simulink模型Fig.6 Simulink model of the circuit to be controlled

图中以交流电压源作为电源，由上而下分出3条支路分别连接两个谐波源（以5、7 次电流源并联作为谐波源）和电阻负载，受控电流源视为SAPF 与第2 个谐波源并联，通过向节点3 所在支路注入5、7 次补偿电流，使节点2、节点3 支路的谐波电压含量降到最小。电路中以电阻、电感串联作为线路阻抗。

3.2 数据采集及训练

仿真采集了50 组“补偿电流—谐波电压”数据对，其中每组数据对由4 个量构成，分别为补偿电流幅值及相位（输入）、节点2、3 支路谐波电压幅值（输出）。神经网络结构为2-4-4-2，神经元激活函数为tanh，训练算法为梯度下降法。

其中，35 组数据为训练集（计算神经网络参数）、8 组为验证集（判断何时停止训练），剩余7组为测试集（计算神经网络精度）。图7 为3 集的均方误差随迭代数变化折线图，由图可知，验证集误差于第17 代达到最小，取第17 代参数为最终参数。

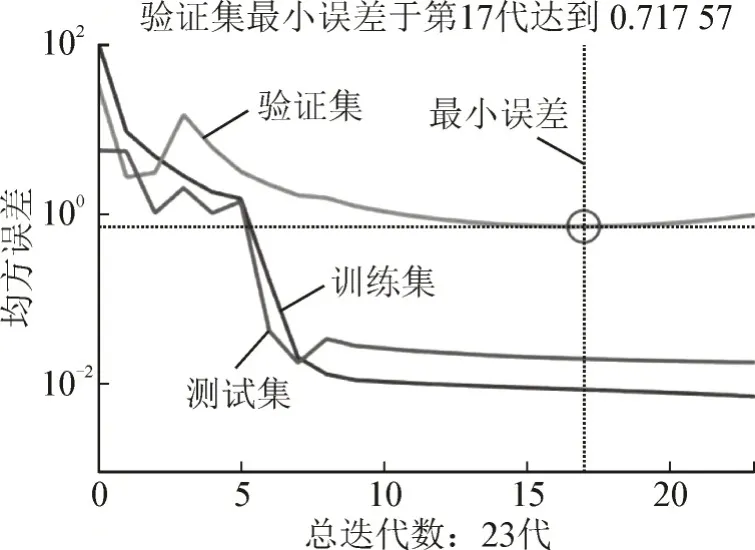
图7 3个数据集的均方误差随迭代数变化折线图Fig.7 Line chart of mean squared errors of three data sets with iteration variation

此时，3 个数据集对应的神经网络模型输出与实际数据的线性拟合图见图8，图中每个数据点横坐标代表1 组输入所对应的实际输出，纵坐标代表同一组输入对应的模型输出。因此，若模型完全精确，数据点应处于正比例函数的直线上，也即拟合后的直线越接近正比例函数，模型效果越好。3 个数据集的拟合直线与正比例函数接近，满足要求。

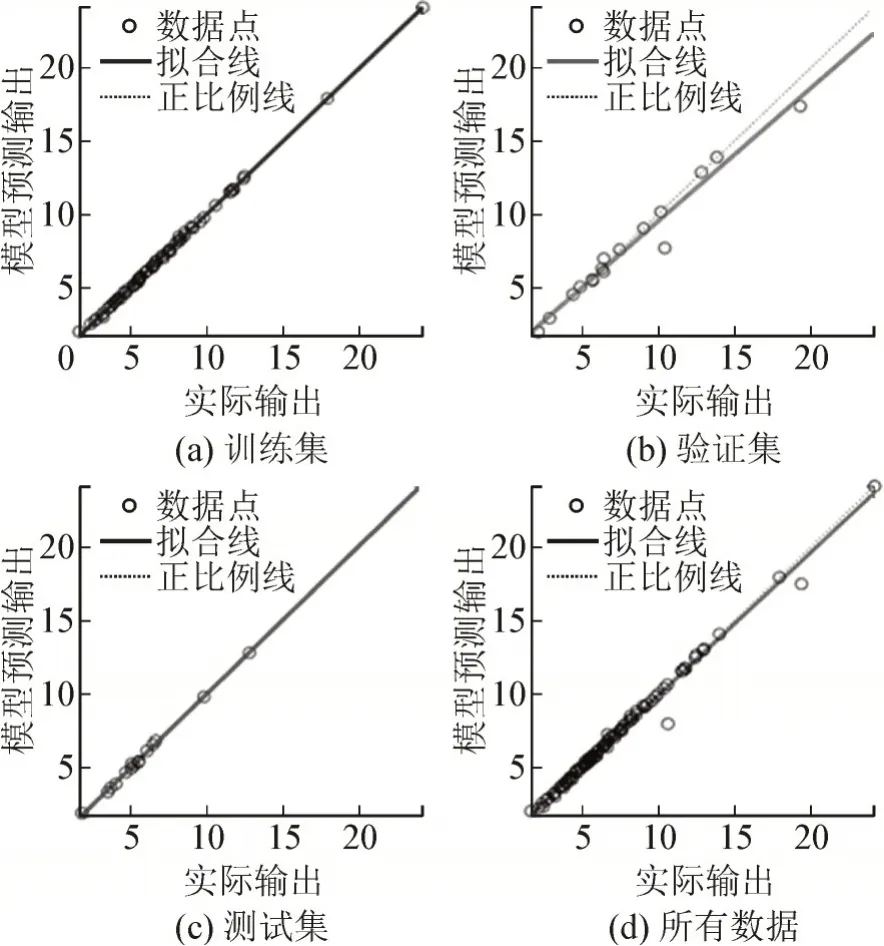
图8 3个数据集的模型预测输出与实际输出的线性拟合图Fig.8 Linear fitting diagram of model predicted output and actual output of three data sets

采样过程中，每0.02 s 变换一次补偿电流输入，因此50 组数据对所用时间为1 s，其后0.1 s 将输入置0，以便与之后的治理比较，1.1 s 后，向电路注入计算所得的最优补偿电流。整个仿真过程中，5、7次补偿电流的幅值、相位变化见图9，其中上边折线为幅值，下边折线为相位。

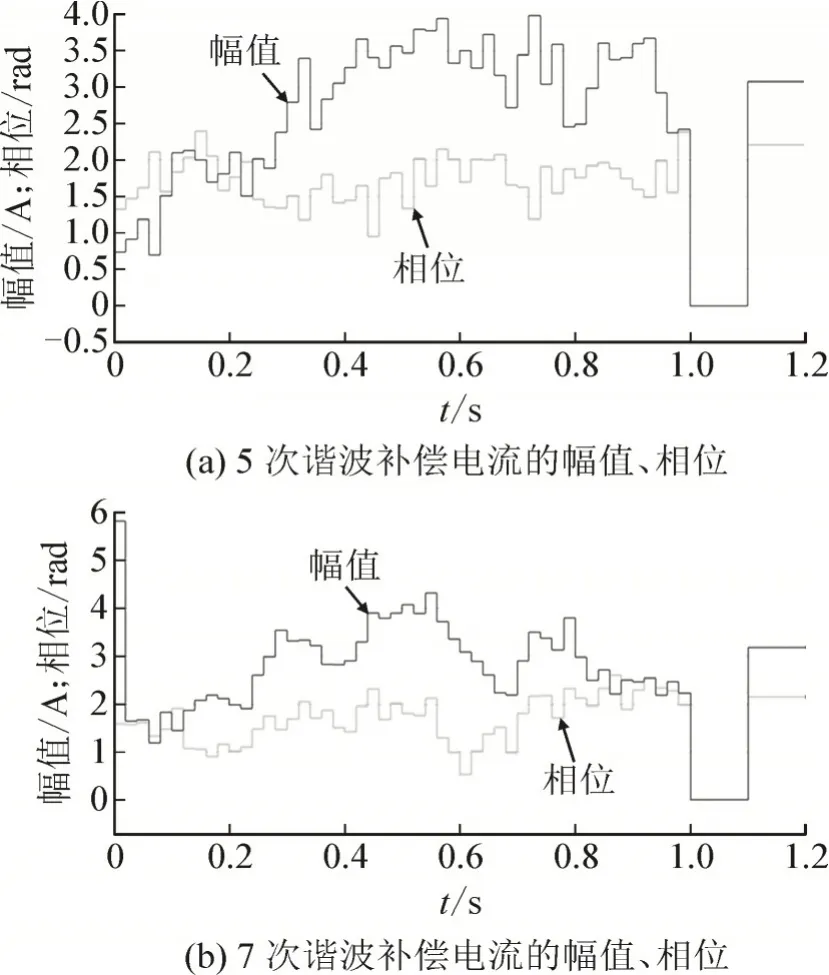
图9 5、7次谐波补偿电流波形Fig.9 Waveform of 5th and 7th harmonic compensation current

最终计算得出5 次最优补偿电流幅值相位分别为2.212 与3.076，7 次最优补偿电流幅值相位分别为2.154 与3.18。与此相对，利用向电路依次注入电流经过遍历得到的最优解（精确度为0.1）分别为5 次电流幅值2.1、相位3.1，7 次电流幅值2.2、相位3.1，初步说明了最优解的有效性。

图10 为节点2 支路电压幅值变化与波形变化情况，其5 次电压幅值治理前后变化为由9.945~2.514，7 次电压幅值为11.71~3.348。1.1 s 注入最优补偿电流，波形由此变化，节点2 所含5、7 次谐波电压均得到抑制。

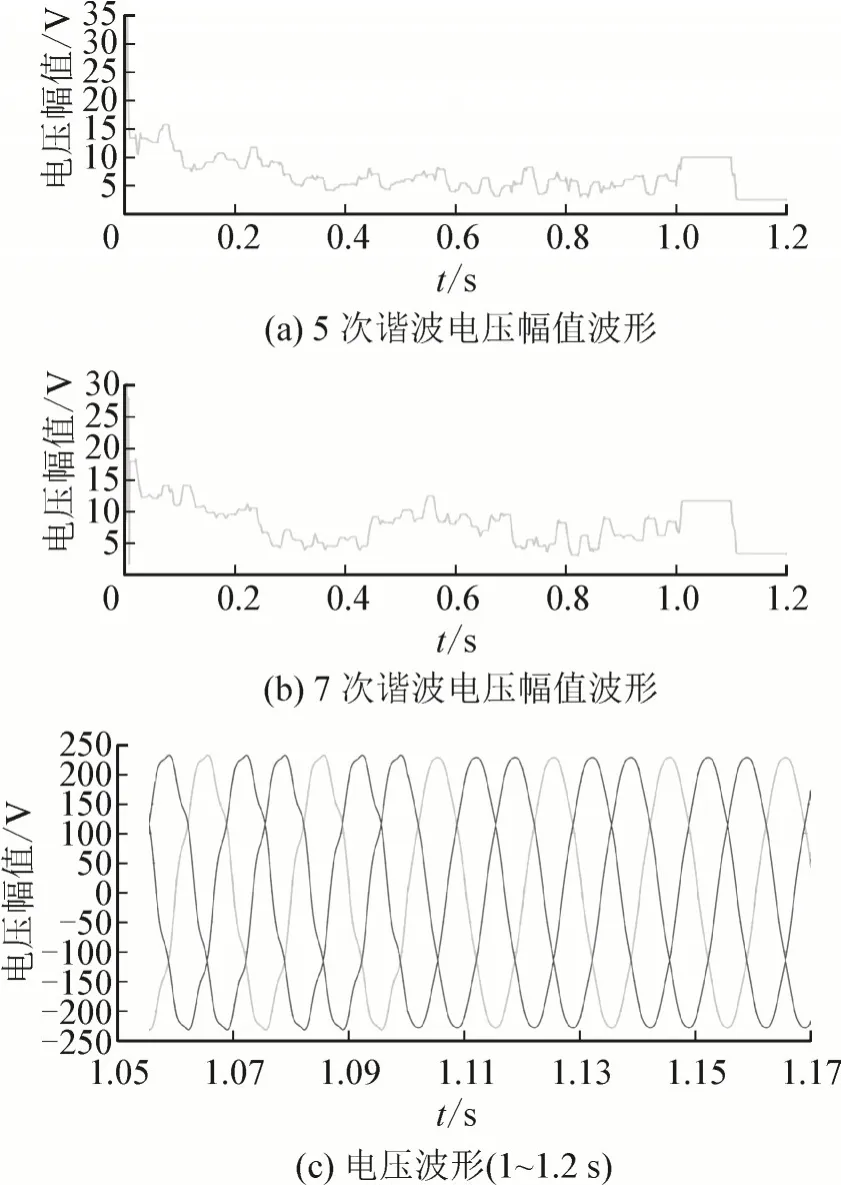
图10 节点2支路电压幅值与波形Fig.10 Voltage amplitude and waveform of branch circuit of node 2

图11 为节点3 支路电压幅值变化与波形变化情况，其5 次电压幅值治理前后变化为由10.23~6.672，7 次电压幅值为11.82~7.825。1.1 s 注入最优补偿电流，波形由此变化，节点3 所含5、7 次谐波电压均得到抑制。

由图10、图11 可知，基于BP 神经网络建模的谐波综合治理算法考虑到了系统整体的谐波传播分布，从而实现了利用单台SAPF 综合治理谐波的效果。与此相对，图12、图13 所示为SAPF采取传统就地补偿方式时节点2、节点3 的5、7次谐波电压幅值。

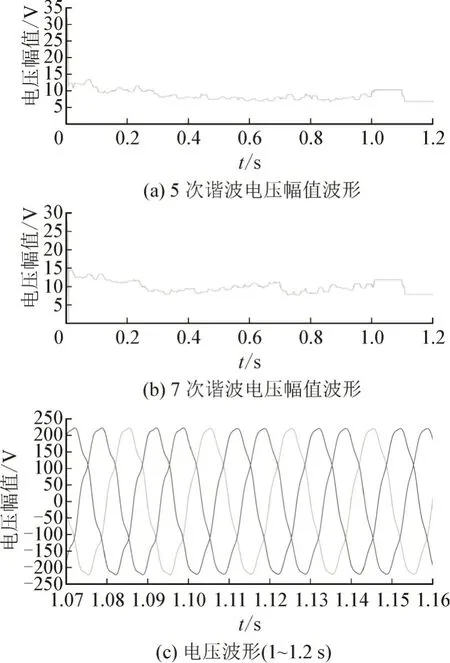
图11 节点3支路电压幅值与波形Fig.11 Voltage amplitude and waveform of branch circuit of node 3

图12、图13 分别代表采用就地补偿工作方式时节点2、节点3 的5、7 次谐波电压幅值波形，SAPF 每0.06 s 检测流经节点3 的5、7 次谐波电流，更新其输出。

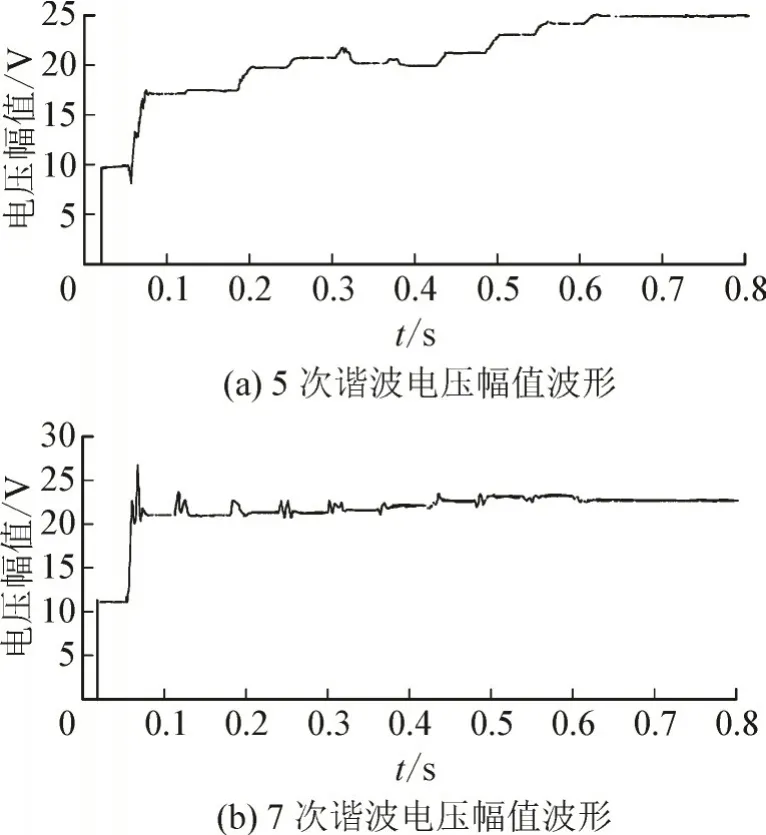
图12 就地补偿时节点2支路电压幅值与波形Fig.12 Voltage amplitude and waveform of branch circuit of node 2 in local compensation

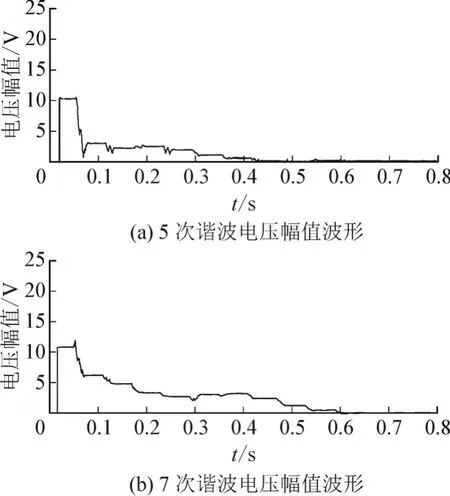
图13 就地补偿时节点3支路电压幅值与波形Fig.13 Voltage amplitude and waveform of branch circuit of node 3 in local compensation

由图可知，由于SAPF 安装于节点3，因此节点3 的5、7 次谐波电压随着治理过程逐渐降低，直至稳定于0，节点2 的5 次谐波电压幅值则由9.945升至24.832，7 次谐波电压幅值由11.71 升至23.014，可见由于未能考虑系统整体的谐波分布，使SAPF 的输出破坏了谐波之间原本的“平衡”，从而导致节点2 谐波含量进一步上升，系统整体谐波状况更为恶化。

综上所述，不同于采取就地补偿工作方式的有源电力滤波器，基于BP 神经网络建模的有源电力滤波器将系统整体的谐波分布也纳入考量，从而得以均衡调节自身输出，维持系统整体谐波含量最小。

4 结语

本文研究了基于神经网络黑箱建模的并联型有源滤波器谐波综合治理控制算法。由传统单点就地补偿算法出发，分析了传统有源电力滤波器就地补偿工作方式在多谐波源系统中的局限性，基于此，说明了综合治理所需模型的特点，即综合考虑系统整体的谐波分布情况，进一步提出了神经网络建模的方法，通过建立补偿电流与节点电压之间的数学模型，得以在无需电网参数的条件下计算使各待治理节点谐波电压幅值平方和最小的补偿电流。并根据全连接神经网络对于可测函数无限逼近的能力，从理论上证明了其可行性，进而将多谐波源电网的谐波综合治理问题化为优化问题进行求解。之后通过Matlab/Simulink 仿真，建立了电路模型，验证了该方法的可靠性。

基于神经网络建模的方法需要采集数据对，但当采集数据时，电网完全没有得到治理，如能在采集数据时采用一些优化算法，则可以在不失随机性地采集数据的同时，对电网谐波进行预治理，从而在治理前即可降低部分谐波含量。

采集所得输入数据实际上是由幅值、相位分别构成，不能很好反映谐波的特性，如能将电流、电压相量作为一个数据进行训练，模型的性能会更好，对于数据量的要求也会随之降低，例如可将幅值与相位重新合成为相量，采用复数值神经网络直接处理电流相量与电压相量的关系，不仅令物理量之间的关系更为明显，也将极大地提升本方法在实际工程中的实用性。