混合无功补偿系统模型预测直接功率控制策略

杨国，陈洁，朱亮亮，郑凯凯，陈文魁，徐康亮

（1.新疆大学电气工程学院，乌鲁木齐 830046；2.国网新疆电力有限公司克州供电公司，新疆 克州 844000）

0 引言

近年来，随着电力电子装置在人们生产生活中的广泛应用，这些非线性、不平衡的负荷使电网电压和电流发生畸变，带来了较为严重的谐波问题，并且由于配电网中存在着大量感性负载，造成了电网功率因数低、电压跌落等电能质量问题[1-5]。为了解决以上问题，改善电能质量，无功补偿装置越来越多地被应用到了电网中。

目前配电网中应用较为广泛的无功补偿装置主要是静止无功补偿器（SVC），SVC 通常由固定电容器与晶闸管控制电抗器并联组成，其优点是结构简单，成本较低，但是存在投切速度慢、抑制谐波效果差和电压闪变等问题[6-8]。静止无功发生器（SVG）由于其响应速度快，谐波抑制能力强，无功补偿效果好，在无功补偿领域使用日益增多，但其成本约是SVC 的2-3 倍，限制了其在配电网中的大面积应用[9-11]。因此根据结合两者优点的SVC+SVG 混合无功补偿系统得到了发展空间[12-15]。

混合无功补偿策略在国内已经有了部分研究，文献[16]提出了将模型预测控制应用于SVC 与静止同步补偿器（static synchronous compensator，STATCOM）的协调控制器设计，替代了传统PI 环节，避免了PI 控制参数难以整定和全局优化困难等问题，并研究了两者之间的交互影响问题，但没有对SVC 与STATCOM设备的各自特性进行分析，对于在实际工程应用中涉及的容量分配问题也缺乏讨论，仅是在理论层面对控制策略进行了改进与优化。文献[17]提出把SVC 与SVG 在系统内进行整合用于混合无功补偿，根据SVC 与SVG 在响应速度上的差异，将大容量无功交给SVC 补偿，小容量无功由SVG 补偿，但在两者容量分配上，仅仅是提出了设想，没有详细阐述具体分配措施。文献[18]提出将SVG 以模块的形式嵌入SVC 中，把两者视作一个整体，在经济层面上有一定优势，但是仍采用PI 控制，难以确保系统的动态响应以及鲁棒性，在补偿容量的分配上，仍是通过主观分配，并未提出新的解决方案。

在前人探究与努力的基础上，本文提出一种基于无功功率分解的SVC+SVG 模型预测直接功率控制策略。首先依据SVC 与SVG 二者响应速度不同，利用互补式经验模态分解算法（complementary ensemble empirical model decomposition，CEEMD）对系统所需无功进行分解重构，得到高频无功和低频无功，进而确定两者无功补偿容量，再通过模型预测控制器使二者各自产生所需补偿无功，对系统进行无功补偿。最后在Matlab/Simulink 中对所提方案进行了仿真分析，验证了所提方法的有效性。

1 含SVC与SVG的系统模型

1.1 系统数学模型

图1 为由SVC 与SVG 构成的系统电路结构，出于对后期改造、使用、维护的灵活性的考虑，并且在系统内部SVC、SVG 也是分别进行控制的，所以在此模型中，将SVC、SVG 作为独立模块。由于SVC、SVG是并联在电网母线上的，因此会存在如下两种情况：

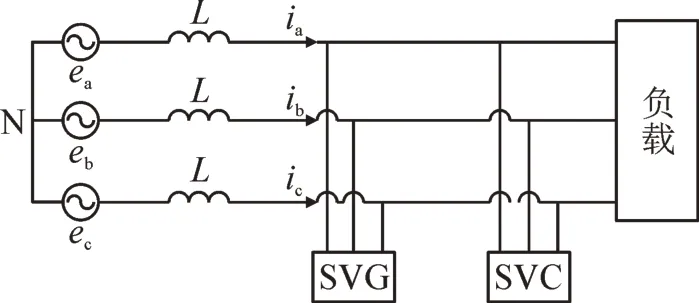
图1 系统结构图Fig.1 Structural diagram of system

1）SVC 靠近电源侧，SVG 靠近负载侧，这种情况下SVG 仅能抑制负载谐波，无法补偿SVC 运行时产生的谐波。

2）SVC 靠近负载侧，SVG 靠近电源侧，此时SVG 也可以兼顾到SVC 的谐波抑制，杜绝SVC 对系统侧电网污染。因此本文采用第2 种方案。

图1 中ea、eb、ec和ia、ib、ic分别为三相对称电网相电压、三相相电流，L为连接电抗。在三相电网电压平衡时，根据基尔霍夫定律可得静止αβ 坐标下的系统动态方程为

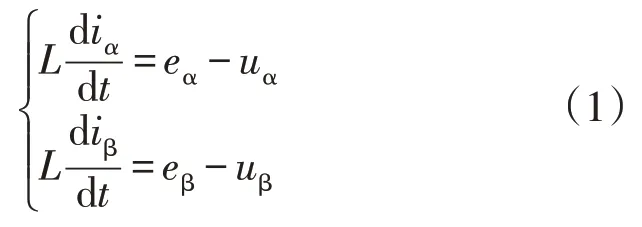
式中：iα、iβ和eα、eβ分别为三相电网电流和电压在α、β轴上的分量；uα、uβ为负载侧电网电压在α、β轴上的分量。

根据瞬时无功功率理论，系统电网负载侧的瞬时无功功率可表示为

对式（2）求导，可得系统瞬时无功变化率为

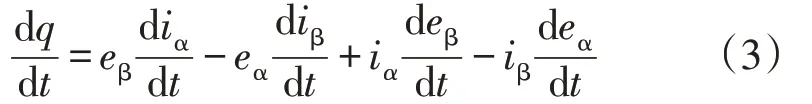
1.2 SVC与SVG的响应时间

SVC 与SVG 的响应时间特性是本文划分高频无功、低频无功的重要依据。SVC 由于受晶闸管触发延迟导致其响应时间在20~40 ms 之间，SVG 中的IGBT 体现出了电力电子开关的优势，可实现高频快速投切，SVG 的响应时间一般不大于5 ms。这意味着无功功率中频率较高的部分SVC 不能实时跟踪进行补偿。通过CEEMD 算法对无功功率进行分解，将SVC 可实时响应的部分交给SVC 补偿，其余高频部分由SVG 进行补偿。

取SVC 响应时间最大值40 ms，频率与时间的关系为

式中：F为频率；T为SVC 最大响应时间。

根据公式可知SVC 可有效补偿频率不高于25 Hz的无功功率，而高于25 Hz 时，受其自身特性影响，会造成过补偿或欠补偿的情况。因此将频率不高于25 Hz 的无功定义为低频无功，将频率高于25 Hz的无功定义为高频无功，过补偿与欠补偿示意图见图2。混合无功补偿系统由SVC 补偿低频大容量无功，SVG 补偿高频小容量无功，可做到盲点覆盖，实现无级投切，精准补偿，示意图见图3。

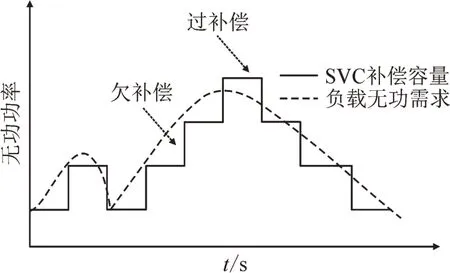
图2 欠补偿、过补偿示意图Fig.2 Schematic diagram of under compensation and overcompensation

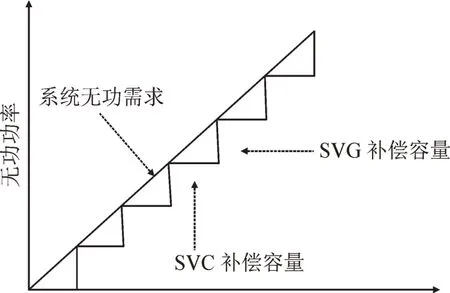
图3 混合补偿示意图Fig.3 Schematic diagram of hybrid compensation

2 基于CEEMD的无功功率分配

电网中无时无刻都有负载投入运行和从电网切除，因此无功功率信号是一种随机性、非线性信号。采用传统频域方法分解效果不理想。1988 年Huang 等人提出经验模态分解算法（empirical model decomposition，EMD），适用于处理非线性、不平稳信号，但存在模态混叠和边界效应等问题[19]。为解决模态混叠问题，文献[20]提出通过向原始信号加入一系列白噪声信号，解决模态混叠问题的集合经验模态分解算法，但重构信号中存在残留白噪声大的缺点。

本文采用互补式集合经验模态分解算法（CEEMD）来分解无功功率信号，通过增加正负白噪声对能够完全消除白噪声对重构信号的影响。

原始无功功率具体分解过程如下：

1）对原始无功功率信号qw(t)中加入正负白噪声对(-1)va0ni(t)后对信号进行一次EMD 分解公式为

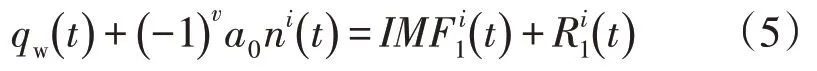
式中:v=1,2，i=1,2,…,M2，M2 为原始无功功率加入的正负白噪声对数；为无功功率剩余分量，对M个固有模态分量求其平均值得到第1 个固有模态分量为

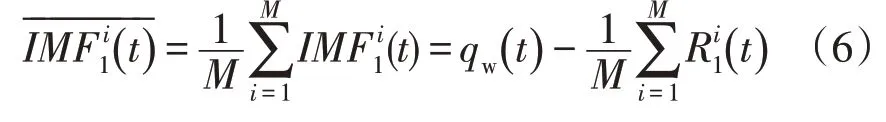
式中完成M次集合平均后噪声对相互抵消，模态分量中不存在白噪声信号。

2）提取第1 个模态分量并得到剩余无功功率分量为

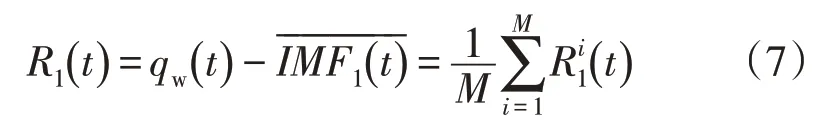
对剩余无功功率加入经EMD 分解的噪声分量，进行EMD 分解。

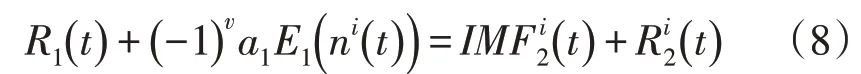
对上式M个固有模态分量结合平均后得到第2 个固有模态分量为

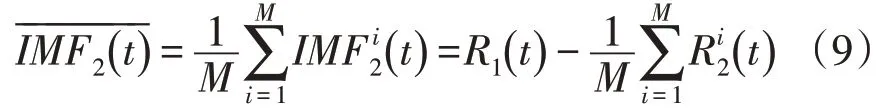
无功功率剩余分量为

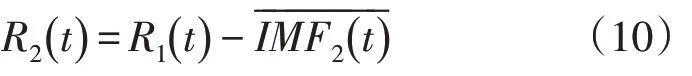
3）循环步骤2），直到提取原始无功功率中所有固有模态分量。

4）经CEEMD 分解后重构信号qw(t)可表示为

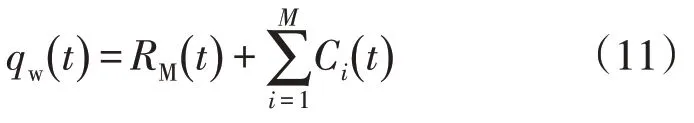
式中：RM(t)为残余信号；Ci(t)为第i(i=1,2,…,M)层固有模态函数，并以频率由高到低依次分布，然后将IMF 分量通过滤波器重构得到原始无功功率信号的低频部分和高频部分，获得SVC 和SVG 的参考补偿功率。

低频部分（SVC 补偿功率）为

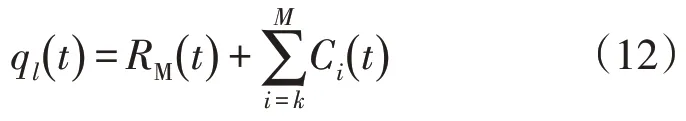
式中，k为滤波器的滤波阶数。

高频部分（SVG 补偿功率）为

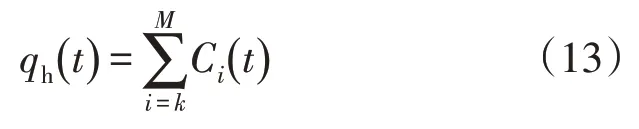
3 模型预测直接功率控制

3.1 预测模型

模型预测控制是通过系统预测模型，根据历史某段时间和当前时刻的状态量和控制量，预测系统未来一段时间的状态，然后在每一采样时刻寻求一个有限时域最优控制[21-25]。

假设第k个采样周期中，无功功率的导数值为A，公式为

用线性一阶方程代替式（15）中的导数方程，则每个开关周期结束时的无功预测值为

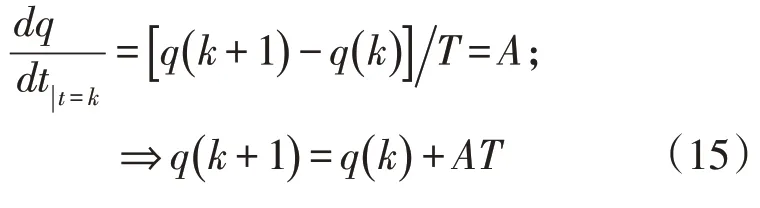
式中：T为采样周期；q(k)为k时刻采样的无功功率值；q(k+1) 为k时刻对k+1 时刻无功的预测值。

3.2 评估函数与反馈校正

为了获得较好的补偿效果，控制算法的目标是使并网无功功率值尽可能接近给定无功功率值，为了达到这个目的，针对每个时刻的无功功率预测值，采用评估函数进行评估，使无功功率的误差值在每一个控制周期结束为最小。

对于模型预测直接功率控制，评估函数可以采用以下几种形式：

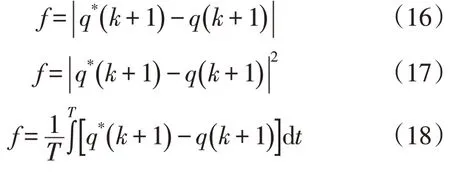
式中：q*(k+1)为k+1时刻的无功参考值。

式（16）所示的评估函数运算量最少。式（17）中的评估函数在相同条件下能产生较式（16）更大的f值，可以更好地改善电流波形，计算量也相对较大。式（18）采用积分的形式，将控制周期内的无功功率纳入考虑范围，具有更好的无功跟踪效果，但对其他方面的控制性能影响较大。以上3 种形式的评估函数，在足够高的系统控制频率下，性能仅存在微小差别，因此本文选用式（16）作为无功预测的评估函数。

在实际系统中，系统进行采样、量化时，由于受到各种干扰因素的影响会产生误差和预测模型自身可能出现失配的情况，会对被控系统的预测产生一定的误差。为了降低上述情况对控制的影响，利用当前时刻的无功实际值反馈回来进行校正，构成闭环优化。

在k时刻采样可以得无功的实际输出值q̂(k)，比 较q̂(k)与(k-1) 时刻对k时刻的无功预测值q(k-1) 可得其偏差信号。

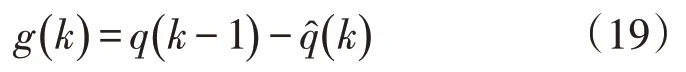
根据g(k)对下一时刻的偏差预测为

式中，h为反馈系数。

3.3 整体控制策略

系统整体控制策略框图见图4，主要由三部分构成：无功功率检测与分解、模型预测直接功率控制和无功补偿执行部分。其基本运行步骤如下：

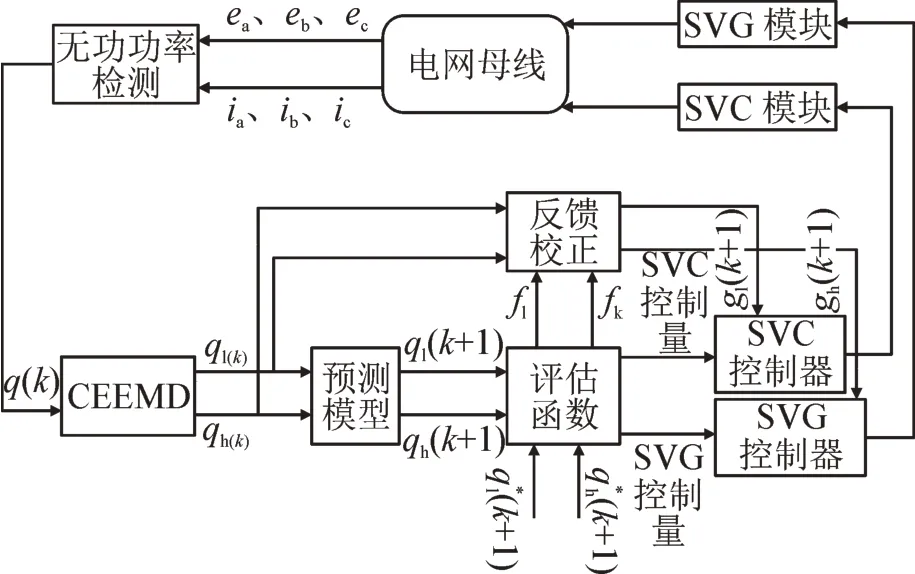
图4 整体控制策略框图Fig.4 Block diagram of overall control strategy

由检测装置对并网点电流、电网电压进行采样得到k时刻电网所需无功功率q(k)，将q(k)经CEEMD 分解重构后得到低频无功ql(k)，即SVC 补偿容量；高频无功qh(k)，即SVG 补偿容量。

根据预测模型预测出下一时刻无功补偿预测量ql(k+1) 、qh(k+1) ，经过评估函数计算无功误差最小后输出SVC 与SVG 参考控制量，经偏差预测信号gl(k+1) 、gh(k+1) 校正后送往控制器，控制SVC、SVG 产生补偿功率。

4 仿真验证与分析

为了验证该控制策略的有效性和无功功率分解的可行性，在Matlab 仿真环境下搭建了上述混合无功补偿系统的仿真模型，模型具体参数如下：电网线电压380 V，频率50 Hz，加入固定负载与小额动态负载。仿真中设置固定负载1（P：10 kW，Q：8 kvar），在0.2 s 时投入固定负载2（P：10 kW，Q：5 kvar）以验证其动态性能，从始至终加入以40 Hz 频率投切的小额负载以提供高频无功功率。

无功信号经CEEMD 算法分解重构后，由模型预测控制得出SVC、SVG 控制信号，并控制两者各自输出补偿功率。为验证无功分解的有效性，将二者输出功率进行对比，二者输出功率见图5。

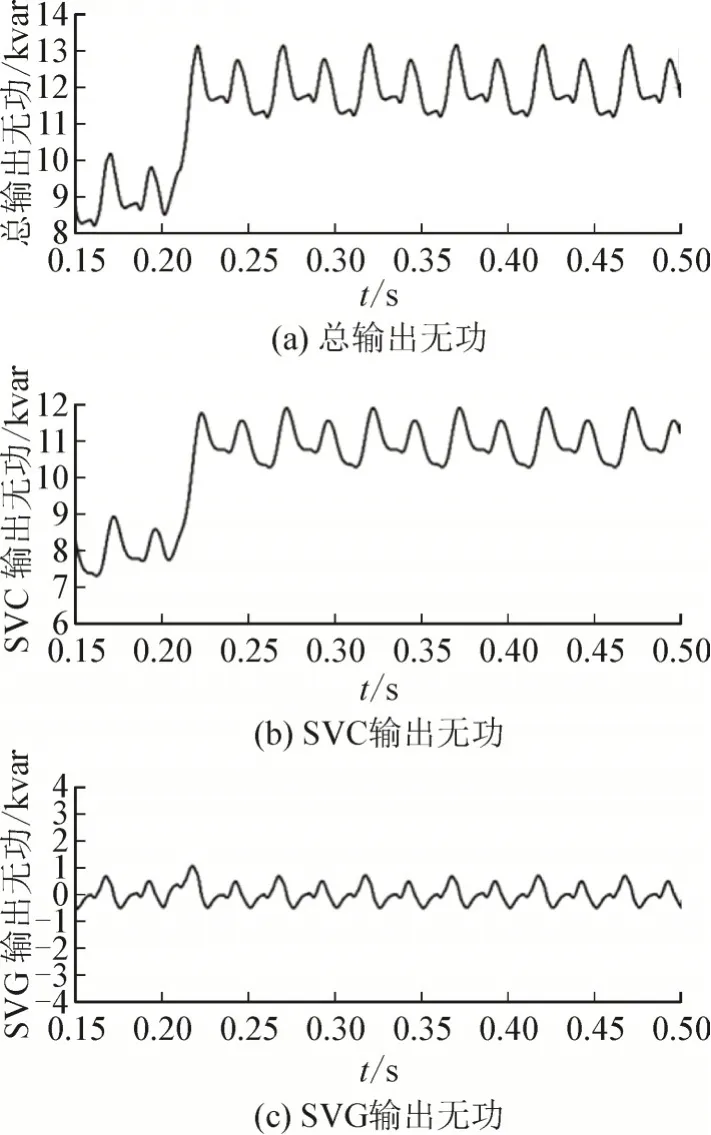
图5 SVC与SVG输出功率Fig.5 Output power of SVC and SVG

由图5 可以看出经功率分解后可以有效降低系统中SVG 容量配置，为验证在工程应用中是否适用，以现场数据为例，验证功率分解的有效性。本文使用新疆克州某地10 kV 公变无功功率数据，选取2018年9 月3 日某时段部分数据，采样周期为0.8 s，共计3 000 个点。经CEEMD 算法分解重构后图形见图6。

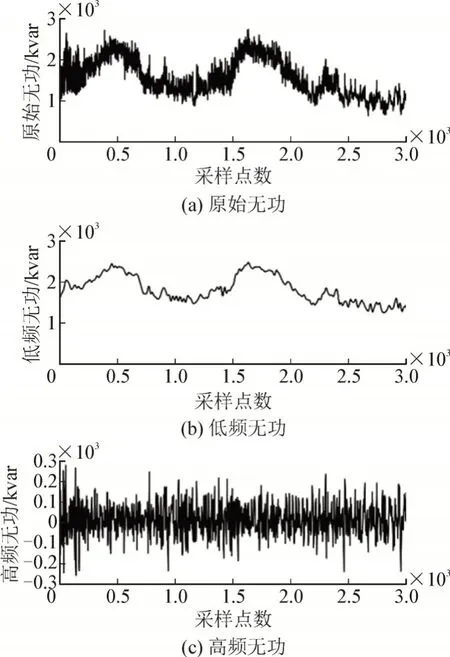
图6 实际无功分解Fig.6 Actual reactive power decomposition

根据分析无功数据分解重构后的波形可以得到，在此时段此公变，可通过查表法确定SVC：SVG容量比值为7：1，在工程应用中，相同容量下SVC的成本约是SVG 的1/3，在上述无功情况下，本文所提方案具有较好的经济性。

为验证模型预测控制的动态性能，以SVG 直流侧电容电压为参照，其波形见图7。

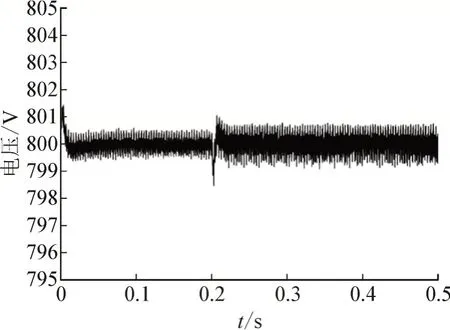
图7 SVG直流侧电压Fig.7 Voltage at DC side of SVG

由图可知，当系统在0.2 s 加入感性冲击负荷时，在模型预测控制下，SVG 直流侧电压经过小幅超调后很快便进入稳定状态，基本稳定在800 V，仅存在微小波动，证明了模型预测控制具有优异的动态性能。

在系统无功补偿效果方面，以A 相电压电流为例，补偿前A 相电压电流见图8（a），从图可以看出，由于系统中投入感性负荷，A 相电流滞后于电压，系统功率因数较低。补偿后A 相电压电流波形见图8（b），电压与电流恢复为同相位，系统功率因数得到明显提升。

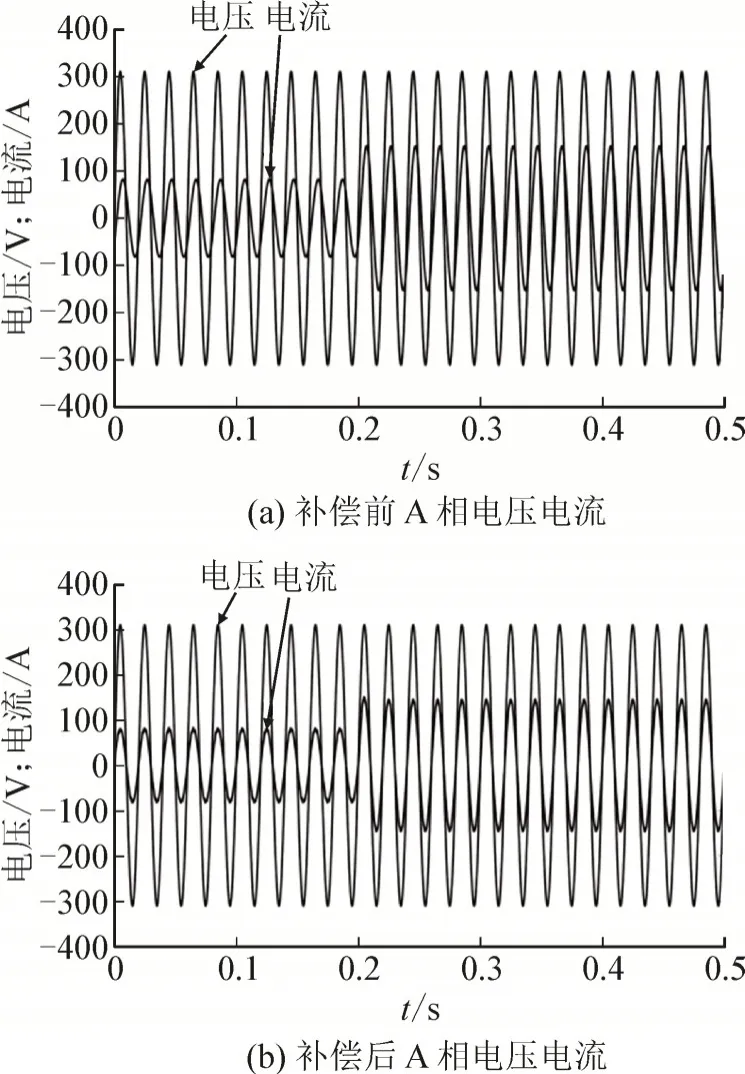
图8 A相电压电流Fig.8 VoltageandcurrentinphaseA

5 结语

通过对SVC 与SVG 的设备响应特性进行分析，确定了二者能够补偿的无功频率范围，首次将基于CEEMD 算法的频率分解应用于混合无功补偿中，并对混合无功补偿系统提出了模型预测直接功率控制策略，对现场真实数据进行CEEMD 分解重构后表明了所提方案的可行性，最后搭建了仿真模型验证了本文所提策略具有良好的动态性能以及无功补偿能力。因此，本文研究的基于无功功率频率分解的混合无功补偿方案，对现有SVC 装置进行改造提出了可行方案。