基于迁移多搜索器Q 学习算法的碳能复合流无功优化
2022-03-03唐建林余涛肖勇钱斌王浩林
唐建林,余涛,肖勇,钱斌,王浩林
(1.南方电网科学研究院有限责任公司,广州 510663;2.广东省电网智能量测与先进计量企业重点实验室,广州 510663;3.华南理工大学电力学院,广州 510641)
0 引言
在《2019 年世界能源展望》中,国际能源署提出了各国政府必须采取紧急行动以实现脱碳目标,预计到2040 年,风能和太阳能将成为主要电力来源。为了解决能源与环境之间的矛盾,在公众环保意识日益增强的今天,电力行业必须改变能源结构、降低污染和大气排放水平。目前从国内的研究现状可以看出,国家电网公司和南方电网公司也根据各自的实际情况开展节能减排研究,积极地提出了各个阶段性的减排目标、低碳生产计划和相关技术手段,对节能减排承担了一定的社会责任。
目前来讲,关于低碳电力的研究,文献[1]针对包含电-气-热的综合能源服务商在电力-天然气市场中的可调度潜力,搭建起了考虑综合能源服务商需求响应的电力系统低碳运行优化调度模型,提出了包含碳排放量的综合能源服务商优化运行策略。从优化结果表明,碳交易机制及综合能源服务商需求响应是综合能源系统减少碳排放的有力措施。文献[2]在可再生能源广泛接入的背景下,以发电成本和碳排放量的加权和为目标函数,优化后的结果能够对整个系统的碳排放量进行综合管理,而且能够为可再生能源的接入提供位置指导。文献[3]运用生命周期分析方法,将综合能源系统中不同能源链迁移转化过程产生的碳排放归一化。得到的碳排放系数指导综合能源系统由高排放能源消耗变为低排放能源消耗,为综合能源系统低碳化建模打下了理论基础。文献[4]建议国家在以市场机制开展碳交易推动节能减排的同时,需要建立起碳市场和电力市场的联动协同机制,并且将碳成本依附在电价中。文献[5]在节能减排的过程中,我国需要把碳税作为财税手段,碳交易作为市场手段,市场手段和政府引导相互配合,协调发挥各自的作用。文献[6]研究碳市场对清洁能源发电行业的影响,在电力行业碳排放权交易市场的建立背景下,大力发展清洁能源能够大大减少碳排放量。
由于电网运行环境的复杂性,对于碳排放的责任主要归在了发电侧,倘若无法将电力系统中发电部门-输变配电部门-用电部门的碳排放进行均摊,则无法调动起电网侧、用户侧的积极性。对于国家来讲,电力企业的碳排放计算比较宏观,无法精确地评价各个环节的碳排放量,很难指导电网企业准确调度,让CO2的排放量降低。
碳能复合流无功优化模型是一个多变量多约束的非线性规划问题。目前来看,一般最常用的求解方法主要分为两类:经典数学方法和人工智能算法两种类型。然而,传统法如牛顿法、二次规划法和内点法等都依赖于确定的系统模型,具有求解时间短、收敛性可靠等优点。但是当电力系统的模型中约束条件变得复杂、存在多个不连续变量和多个极值最优解等情况时,这类方法的全局收敛性就会变得非常差,容易陷入局部最优。在优化方法的另一分支中,人工智能优化方法已经非常成熟。人工智能方法具有应用范围广、灵活性高,并且不依赖于具体的电力系统数学模型。但是算法的优化能力跟适应度的值有关。目前关于强化学习的研究层出不穷,这类算法通过不断地探索试错和环境交互来实现策略优化,具有强大的记忆自学习能力。因此有必要将强化学习和群智能算法相结合,用于解决复杂的非线性问题。
在此背景下,本文针对电力系统的碳-能复合流无功模型的优化进行了研究。考虑到电网的低碳要求,将碳排放考虑到无功优化问题中,提出了考虑低碳、经济、安全的碳能复合流无功优化新模型。提出的迁移多搜索器Q学习算法,能够给出理想的碳排放方案,并且能够用到其他更复杂的电力系统优化模型中,具有一定的实用价值。
1 碳能复合流无功优化模型
1.1 碳能复合流模型基础
为了描述碳排放分布在各个节点、各条支路的状态,本文给电网拓扑的每一个器件加上“碳概念”[7]。碳流是一个虚拟网络流,其流动方向也是发电测到电网侧再到用户侧,层层递推,用来衡量碳排放转移过程。类比于电力系统中的电源、网损和负荷,在碳排放流理论中,也有碳源、碳损和碳荷的概念。碳源指的是产生二氧化碳污染的发电机组。对于风力发电机组和光伏发电机组等清洁能源机组是不产生碳排放,所以不能当作碳源。碳荷指的是电力系统的有功功率需求,同时也是用户侧需要承担的相应碳排放责任。碳损指的是电网在进行电能传输中的有功损耗所承担的相应碳排放责任。能流是指在实际电力系统中,有功功率沿着电网络移动的实际潮流。电力系统的碳能复合流见图1。

图1 电力系统的碳能复合流Fig.1 Carbon energy composite flow of power system
假设某一系统含有n个节点,b条支路,s台发电机,Lij表示节点i和节点j之间的支路。根据叠加定理,对于节点i,由发电机节点m对其流入的有功功率Pim和发电机节点m流入至节点i的有功功率跟节点i总流入的有功功率公式为

式中:λim为发电机节点m的有功功率流入节点i的贡献系数,数值上等于经发电机节点m流入节点i的有功功率跟发电机节点m发出总的有功功率的比值;PGm为发电机节点m发出总的有功功率;Pi为节点i的总流入有功功率。
对于电力系统的无损网络来说,从节点i到节点j的两端的功率大小是相同的,即Pij= Pji。但是在实际电力系统中,由于电能在传输的过程中存在发热、阻抗等原因,往往会在支路Lij产生一定的网络损耗ΔPij。此时会出现Pij≠Pji的情况。支路有功损耗公式为

式中:Ui、Uj分别为节点i和节点j的电压幅值;gij为线路Lij的电导;θij为节点i和节点j的相角差。
假设该系统总共含有M台发电机组。那么对于支路Lij所产生的有功损耗ΔPij可拆分成公式为
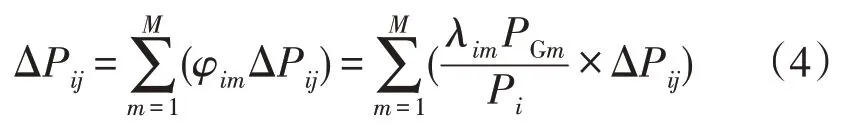
假设NG为全部发电机节点集合,Z为支路集合。那么,整个电网单位时间上总的有功功率损耗就是把所有支路的有功功率损耗进行相加,公式为

根据碳排放理论,电网中的碳排放流跟有功功率的潮流相互依赖,在数值上,碳排放的总量等于发电机的碳排放强度乘以有功功率的大小[8-9]。碳排放强度跟电源的类型有关,风力发电、光伏发电等清洁能源的电厂没有碳排放污染,所以碳排放强度为零;然而对于火力发电等常规能源发电厂,其碳排放强度则是发电机组运行时候的碳排放因子。根据叠加定理,那么对于支路Lij来说,其碳排放损耗公式为

式中,δm为发电机节点m的碳排放强度,其单位为(kg CO2/kW·h),用以衡量产出单位电量所对应的碳排放量大小。
那么,整个电网的总碳排放量Closs公式为
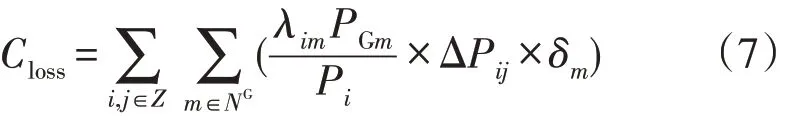
对于发电侧的碳排放量CG,其数值大小为电网侧的碳排放量Closs和用户侧的碳排放量CD的和,公式为
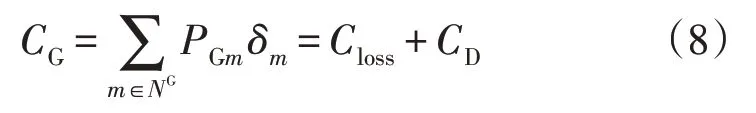
对于发电侧、电网侧和用户侧来说,各主体只关心自身的碳排放量,那么按照碳排放流理论,会存在一部分碳排放重复计算,各主体所承担的碳排放责任会影响整体碳排放量的计量标准。因此,本章将电网侧和用户侧的碳排放责任按照新的分配机制进行重新分摊,公式为

式中:η为发电侧的责任分摊率,其值位于0~1 之间,意思是发电侧比例为η的碳排放转移到电网侧;μ为用户侧的责任分摊率,其值位于0~1 之间,意思是电网侧比例为μ的碳排放转移到用户侧。
所以,对于电网侧来讲,分摊后的碳排放量Cgs公式为

1.2 考虑碳能复合流的无功优化模型
本文所建立的碳能复合流的无功优化模型是在电网满足各约束条件,保证电力安全正常运行的基础上,尽量减少机组的发电成本和降低碳排放量。本章选择有功功率损耗、电网侧的碳排放量和电压稳定分量这3 个优化目标作为研究对象,目的是为了考察电网的经济性、环保性和安全性[10]。经过线性加权后,其目标函数公式为
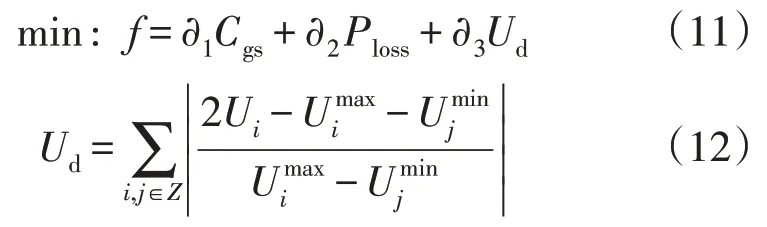
式中:∂1、∂2和∂3均为权重系数,∂1取值处于0~1之间,∂2取值处于0~1 之间,∂3取值处于0~1 之间,并且满足∂1+∂2+∂3=1;Ud为电压稳定值;Ploss为系统的有功损耗值;Ui为节点i的电压幅值,其最大值为;Uj为节点j的电压幅值,其最小值为。
碳能复合流的无功优化模型中的等式约束主要包括有功功率平衡约束和无功功率平衡约束,公式为
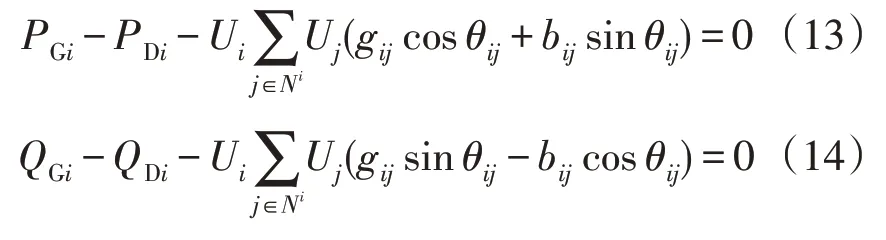
式中:PGi为节点i发出的有功功率;QGi为节点i发出的无功功率;PDi为节点i的有功功率需求;QDi为节点i的无功功率需求;Ni为电网的全部节点集合;Gij为节点i的导纳大小;Bij为节点j的电纳大小。
碳能复合流的无功优化模型中的不等式约束主要有无功补偿装置容量的上下限约束、有载调压变压器约束等等,公式为
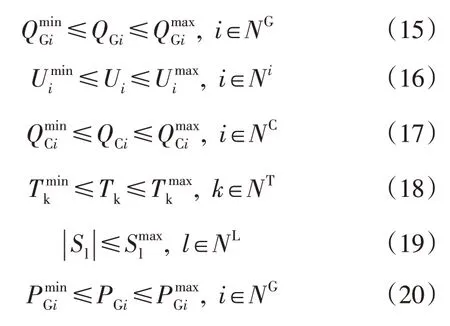
式中:QCi为节点i的无功补偿装置容量大小;Tk为有载调压变压器的变比大小;NC为电网中全部无功补偿节点集合;NT为全部有载调压变压器支路集合;NL为所有支路集合;Sl为线路l的视在容量大小。
2 迁移多搜索器Q学习算法
2.1 信息矩阵
跟多搜索器优化算法类似,迁移多搜索器Q学习算法也有全局搜索器和局部搜索器,每个全局搜索器有自己的搜索范围,局部搜索器隶属于全局搜索器,并在相应的范围内进行搜索。并且在此基础上为每个全局搜索器和局部搜索器构建了相应的信息矩阵(也就是传统Q学习算法的Q矩阵值函数)[11-12],用于全局搜索器跟全局搜索器或者全局搜索器跟局部搜索器进行信息的传递和迁移。
各个搜索器对搜索器所处的环境进行交互,见图2。

图2 迁移多搜索器的学习机制Fig.2 Learning mechanism of transfer multi⁃searcher
具体的交互机制如下:首先,各搜索器通过初始信息矩阵获知所处的环境的状态。然后,迁移多搜索器Q学习算法会将各个搜索器获得的及时奖励进行评估,用来更新其搜索器的信息矩阵。最后,各个搜索器根据当前最新形成的信息矩阵,重新选择新的动作策略,从而不断地对信息进行学习和更新,最终获得搜索器的最优信息矩阵。
传统的Q学习算法由一个主体进行Q矩阵更新,每次进行探索试错,都只能更新信息矩阵中的1 个元素,收敛时间过长。而迁移多搜索器Q学习算法将搜索器群作为多主体对信息矩阵进行并行搜索,全部搜索器共享同一个信息矩阵,在每次搜索迭代过程中,可以同时对多个信息元素进行更新,大大缩短了寻优的时间。
2.2 状态-动作空间降维
本章以Q学习算法的框架来建立多搜索器的信息矩阵,然而Q学习算法没有对状态-动作空间进行降维处理的机制。当电网的规模变大,变量数变多的时候,信息矩阵的规模就会呈幂指数倍急剧增加,容易导致“维数灾难”,使得信息无法存储和迭代计算。例如需要求解的问题含有q个需要优化的变量,第i个变量的动作依此有pi种情况,那么动作可行解的个数就是|A|=p1p2p3...pq。利用分层的思想可以避免类似这种“维数灾难”的问题,但是由于无法很容易地确定目标的分层设计跟联系,算法没法收敛到全局最优解。
所以,本章在分层的思想上进一步提出了一种基于信息传递的维度降低方法,以便各搜索器在对环境进行搜索的过程中对状态-动作空间进行维度降低处理,见图3。

图3 基于信息传递的维度降低Fig.3 Dimension reduction based on information transmission
如图3 所示,迁移多搜索器Q学习算法将高维的动作空间A划分成低维的动作空间从而大规模的信息矩阵Q分解成多个小型的信息矩阵,并且跟变量集对应起来,变量间通过信息矩阵联系起来,各矩阵中的元素为各个变量之间的相关信息[13]。
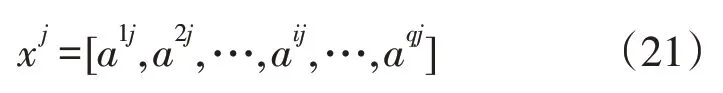

式中,sij为第i个可控变量或者子信息矩阵被第j个搜索器动作选择aij时的状态;J为搜索器j的集合。
确定了上一个变量的动作,下一个变量才能根据上一个变量选择之后的状态选择动作,完成一次信息的传递,并且保持了变量之间的相互联系,最终达到了对信息矩阵维度降低的目的。通过多搜索器的配合搜索优化和状态-动作空间降维后,子矩阵的更新方式为
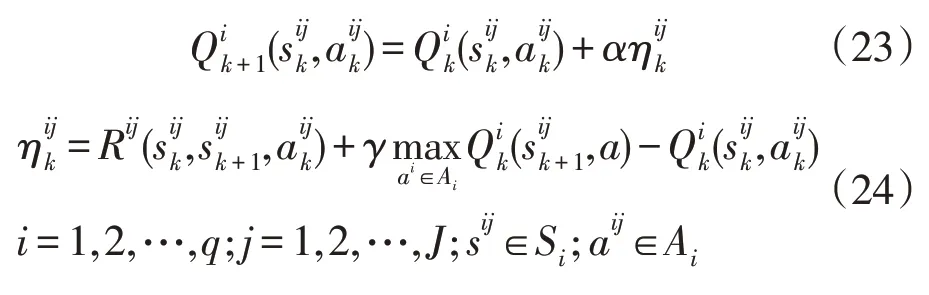
式中:i为第i个可控变量或者子信息矩阵;j为第j个搜索器;J为搜索器群集合;Rij(sk,sk+1,ak)为状态sk在进行第k次迭代时,经过动作ak选择优化后变成sk+1后的反馈值。
当处理连续变量的时候,由于动作的细粒度变高,动作的空间变得异常巨大。信息矩阵难以用有限的空间进行存储,可能会再次面临“维数灾难”的问题,因此有必要对连续变量的问题或者含有连续变量的混合变量问题进行研究[12]。考虑到计算机系统采用的是二进制计算机制,并且数据就是离散的,所以本文打算引入二进制将连续的变量离散化处理,用于问题的快速求解,公式为

式中:i=1,2,…,p,p为连续向量的维度;xi为第i个连续变量;为第i个连续变量的最大值;xmiin为第i个连续变量的最小值;;Hi为第i个连续变量xi对应的二进制向量集,只能取0或者1;q为二进制编码的位数。
二进制编码的状态-动作空间亦需要对其进行状态-动作的降维。对于第i个连续变量xi来说,为二进制编码空间,由于只有0 或者1 两种选择,因此他的下一位的二进制只有0到0、0 到1、1 到0 和1 到1 这4 种情况,所以可以建立一种映射关系见图4,实现二进制空间到状态-动作空间的转变。对于分别与一对应,并作为变量xi更深层次降维后的状态-动作组链,公式为

图4 二进制编码示意图Fig.4 Schematic diagram of binary coding

式中:h为第h个二进制编码;为在第k次迭代第j个主体在变量xi对应的第h个二进制编码处于状态,经过动作选择转变为状态后的环境给予的奖励值。
2.3 动作选择策略
搜索器群在进行信息搜索的过程中,所有的个体都会遇到如何去选择下一步动作的问题。迁移多搜索器Q学习算法的个体在进行动作选择时,一般会采取两种不同措施,要么继续搜索更多的信息,要么在现有信息基础上加以利用。当动作选择偏向于继续搜索更多的信息时,能够提高全局收敛的可能性,但对信息矩阵的利用率不够,算法寻优时间长;当动作选择偏向于在现有信息基础上加以利用,算法的寻优时间就会变短,但是有可能陷入局部最优。
迁移多搜索器Q学习算法的动作选择策略采用的是基于概率分布的多搜索器协同机制。搜索器中的个体是通过分享变量对应的信息矩阵来进行学习。为了减少陷入局部收敛的概率,并且保证拥有较短的搜索时间,对于局部搜索器来讲,依然保持在指定半径范围内进行搜索;而对于全局搜索器来说,采用的是贪婪规则,其公式为

式中:ε为0~1 之间的任意数,并且服从均匀分布;ε0为贪婪因子,决定了个体选择贪婪动作的概率,较小ε0的值可以让算法搜索到全局的最优解,但优化的时间会变长;at为动作概率矩阵Pi个体在全局搜索范围内进行选择的动作策略;全局搜索器在Q值矩阵的基础上按照ε-贪婪规则进行动作的选择,能够明显降低了其全域搜索的盲目性,提高搜索器群对信息的利用能力。Pi的迭代公式为

式中:β为变异因子,表示各个子信息矩阵Qi的离散程度;di为中间过渡矩阵。
所有主体完成搜索进行完动作选择之后,就需要评价每个个体各自的适应度函数,然后对信息矩阵进行更新。本章采用蚁群算法的合作策略制定奖励函数,公式为
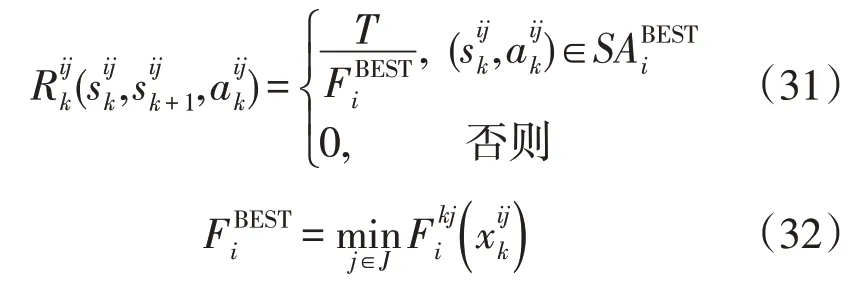
式中:T为正的常数,满足适应度函数跟环境的奖励值成反比的目的;为第k次迭代时个体j的适应度函数;FiBEST为第k次迭代时最优目标函数值;为第k次迭代中最优个体构成的状态-动作对集合。
2.4 信息迁移
多搜索器优化算法对于不同的优化目标采取不同的优化策略,没有对优化目标之间的关联性进行挖掘,也没有充分地利用历史优化目标的相关信息。当优化问题变得复杂,优化变量变多的时候,求解时间就会明显变长,甚至出现无法求解的情况。所以,为了减少收敛时间,迁移多搜索器Q学习算法采用了迁移学习的技术,引入了信息迁移的概念。
首先,通过对大量需要优化的任务进行特征总结,从中归纳出能够区分优化任务的信息标签;然后,对不同类型的优化任务进行预学习,并保存其最优的信息矩阵(状态-动作空间的最优Q值矩阵)到历史任务信息库;接着,通过循环神经网络、深度置信网络等深度学习技术深度挖掘信息标签与最优策略之间的联系并训练得到将来相关任务的优化策略和映射网络;最后,通过输入新任务的相关信息标签,在训练好的映射网络中得到当前任务的优化策略,求解当前任务的初始信息矩阵,就可在保证最优解质量的情况下,快速得到优化结果,见图5。

图5 信息矩阵的迁移Fig.5 Migration of information matrix
本文主要是通过长短期记忆神经网络来实现信息迁移。长短期记忆神经网络(long short⁃term memory,LSTM)是循环神经网络(recurrent neural network,RNN)的改进版,能够弥补RNN 的梯度消失和梯度下降等缺点,见图6。LSTM 神经网络由输入层、隐藏层和输出层三部分组成,其中循环能够让各个隐藏层之间建立联系,将前面时间隐藏层的输出数据作为自身层的输入。因此,当前时刻的信息能够利用上一时刻的数据进行计算。预学习阶段,利用源任务的最优信息矩阵和信息标签来训练LSTM 得到最优的网络权重;在线学习阶段,利用当前新任务的信息标签,就可以通过训练好的LSTM模型来求解出当前新任务的最优信息矩阵。

图6 长短期记忆神经网络原理图Fig.6 Principle diagram of long and short⁃term memory neutral grid
3 基于TMSQ的碳能复合流无功优化求解设计
3.1 算法状态与动作的设计
在实际的电力系统中,发电机端电压需要进行连续地调节[14-17],因此在碳-能复合流无功优化模型需要利用连续变量来描述发电机端电压。而变压器变比和无功补偿装置的投切量用离散变量来表示,所以碳-能复合流无功优化模型是一个混合变量优化模型,在进行状态和动作空间的设计时需要设计成一个混合变量空间。引入二进制将连续的变量离散化处理,并且按照解空间降维的方式对变量进行分解,并且每一个信息矩阵的状态空间都是对应于上一个变量的动作空间,即Si+1=Ai,Ai=[AT;AG;AC],其中AT为变压器变比的动作空间;AG为发电机端电压的动作空间;AC为无功补偿装置投切量的动作空间。
3.2 奖励函数的设计
在碳能复合流无功优化的数学模型中,设计奖励函数时需要考虑到Q学习算法在优化过程中,奖励值越大越好,然而目标函数是追求最小值。根据式(11)给出的目标函数,以及式(13)到式(20)的各种等式约束和不等式约束可以将奖励函数设计成如下式(33)所示。

式中:M为一个正实数;κ为惩罚因子,惩罚因子κ的值选得过小时,则容易收敛到局部最优解,求解效果差,惩罚因子κ的值选得过大时,则增加计算上的困难;Wj为不满足不等式约束的节点个数。
3.3 迁移学习优化
针对电力系统的碳-能复合流无功优化模型,有功功率需求、无功功率需求、电网结构和运行方式等因素都会影响优化的结果。但是在实际电网中其结构和运行方式在很短时间范围内的变化不明显,可以忽略。以15 min 为一个单位,那么一天内总共有96 个优化任务。因此,碳-能复合流无功优化的不同任务特征信息可用有功功率需求Pi=[P1,P2,…,P96]和无功功率需求Qi=[Q1,Q2,…,Q96]区分。TMSQ 算法在进行信息迁移的过程中主要是挖掘历史任务与新任务之间的相似性,本文利用长短期记忆神经网络来对特征信息和最优Q值矩阵之间的关系进行深度挖掘,并得到信息网络[18]。
为了得到不同优化任务的特征信息相应的最优Q值,需要选择大量不同任务数据进行预学习。然后将电网中所有负荷节点的有功功率及无功功率需求输入到长短期记忆神经网络进行训练,得到不同特征信息跟最优Q值矩阵之间的关系。长短期记忆神经网络可以记忆并利用历史信息,训练效率高的LSTM 模型,有效避免负迁移现象。在进行新任务的优化过程时,先将新任务的特征信息输入到训练好的迁移网络中,就可以获得优化策略。再根据优化策略中包含的历史优化经验和初始信息矩阵进行优化就大大减少新任务的优化时间。
3.4 参数设置
经过大量的仿真测试,TMSQ 的性能主要受到学习因子α、折扣因子g、贪婪因子ε0、全局搜索器的个数GS、局部搜索器的个数LS、惩罚因子κ以及奖励因子M的影响,为了保证效率,主要通过最优解的大小和收敛时间两个指标来确定最优参数配置。各参数设置见表1。

表1 TMSQ参数设置Table 1 Parameter setting of TMSQ
3.5 算法流程
值得注意的是,TMSQ 在预学习阶段需要完成所有历史任务的优化,并对所有的信息矩阵进行保存。然后利用这些最优信息矩阵训练LSTM 模型,即可利用信息迁移技术实现碳-能复合流无功优化模型的快速优化。综上所述,利用TMSQ 算法求解碳-能复合流无功优化模型的具体流程见图7。

图7 基于TMSQ的电力系统碳-能复合流无功优化求解流程图Fig.7 Flow chart of reactive power optimization solution of carbon⁃energy compound flow in power system based on TMSQ
4 算例仿真分析
为了测试TMSQ 应用于电力系统的碳能复合流无功优化模型的求解性能,本章在标准节点系统IEEE 118 进行仿真分析,考虑到模型的非凸性并且引入GA[19]、TLBO[20]、CA[21]、GWO[22]、PSO[23]、MSO[24]、Q学习算法这6 种算法进行对比。本文的算例均在CPU 为Intel-i5-4200M、主频2.50 GHz、内存为8G、Matlab2019、Matpower6.1 的计算机环境上。
4.1 仿真模型
本章将IEEE 118 节点测试系统作为碳能复合流无功优化模型的仿真对象,其节点拓扑图见图8。系统基准容量为100 MVA,算例中共有54 个机组和186 条支路,其中选定17 个电压控制节点、3 个无功补偿节点即节点45、节点79、节点109,5 条联络线即线路8-5、线路26-25、线路30-17、线路63-59、线路64-61 作为有载调压变压器变比控制节点。每个节点的发电机类型和各机组碳排放强度见表2。

表2 各机组碳排放强度Table 2 Carbon emission intensity of each generator
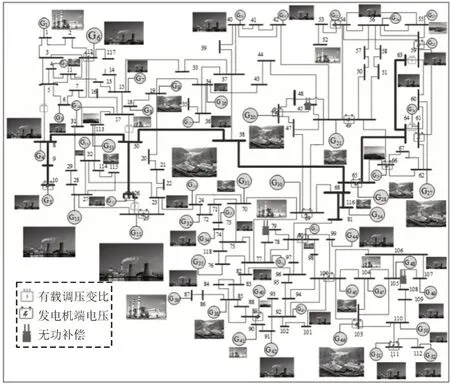
图8 IEEE 118节点拓扑图Fig.8 Topological diagram of IEEE 118 node
发电机端电压取值范围为基准值的1.00~1.06;无功补偿容量的调整范围可用5 个部分构成,分别为基准值的-0.4、-0.2、0、0.2、0.4;有载调压变压器变比的调节范围可以用3 个部分构成,分别为基准值的0.98、1.00、1.02。在算例中,50% 的碳排放责任应由发电侧承担,所以η为0.5;网损所对应的碳排放责任由电网侧全部负责,即μ为1。目标函数的3 个权重系数都设为1/3。
在一天24 h 的范围内选取15 min 为一个断面,可将日负荷曲线划分为96 个断面。电力用户的日负荷曲线按照一定的变化趋势和电压等级进行分类,实际电力系统中同一类型的负荷节点在同一时刻的实时负荷是不一样的。为了增加环境的复杂性,更加贴近实际电网的状态和更好地描述一天范围内电力系统的日变化,首先将负荷节点类型用市政生活、第三产业、重工业、轻工业这4 种来区别,各类型的负荷曲线见图9,源任务、新任务118 个节点负荷样本见图10、图11。
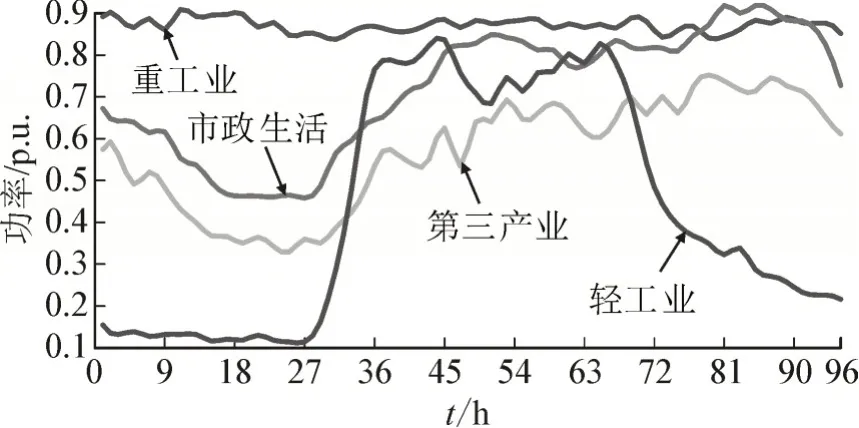
图9 负荷类型日变化曲线Fig.9 Daily variation curve of load type

图10 源任务118个节点负荷样本Fig.10 118 node load samples of source task

图11 新任务118个节点负荷样本Fig.11 118 node load samples of new task
4.2 预学习
图12 为118 节点系统优化任务日负荷曲线,以图12 中的源任务负荷曲线作为学习样本,源任务需要在预学习中跟环境不断交互与探索更新,才能得到不同负荷断面的最优信息矩阵及对应的功率特征信息。并将结果作为后续优化任务的迁移基础。

图12 118节点系统优化任务日负荷曲线Fig.12 Daily load curve of optimization task of 118 node system
以样本62 为例,在IEEE 118 节点系统中,每个信息矩阵在迭代120 步之内就可以收敛到最优信息矩阵,见图13。图14 所示为样本62 的目标函数值收敛情况,样本13 的目标函数值也在迭代130 步之后收敛。TMSQ 算法虽然没有引入迁移技术进行信息矩阵迁移,但凭借Q学习的学习能力和多搜索器的协同搜索两种机制,其搜索时间能够满足优化要求,有良好的搜索性能[25-27]。
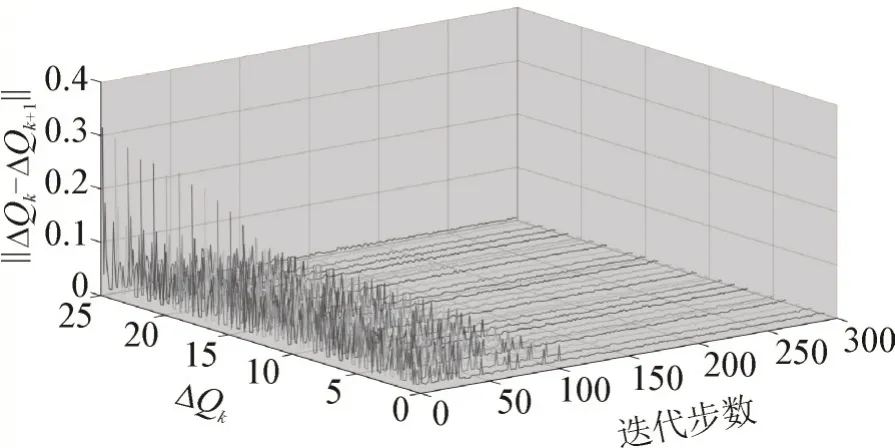
图13 样本62信息矩阵的收敛曲线Fig.13 Convergence curve of information matrix of sample 62

图14 样本62的目标函数值收敛情况Fig.14 Convergence of objective function values of sample 62
4.3 在线迁移学习研究
在完成所有源任务的学习之后,就可以利用所有源任务的最优信息矩阵和特征信息对LSTM 模型进行训练和信息迁移。输入新任务所有负荷节点的有功功率和无功功率就可以立马得到新任务的最优知识矩阵,优化的目标函数能够快速收敛。为对比TMSQ 算法跟其他人工智能算法的优化效果,引入包括GA、CA、GWO、MSO、PSO、TLBO 这6 种常用的启发式算法进行测试分析,所有算法的优化参数均通过仿真测试确定,见表3。
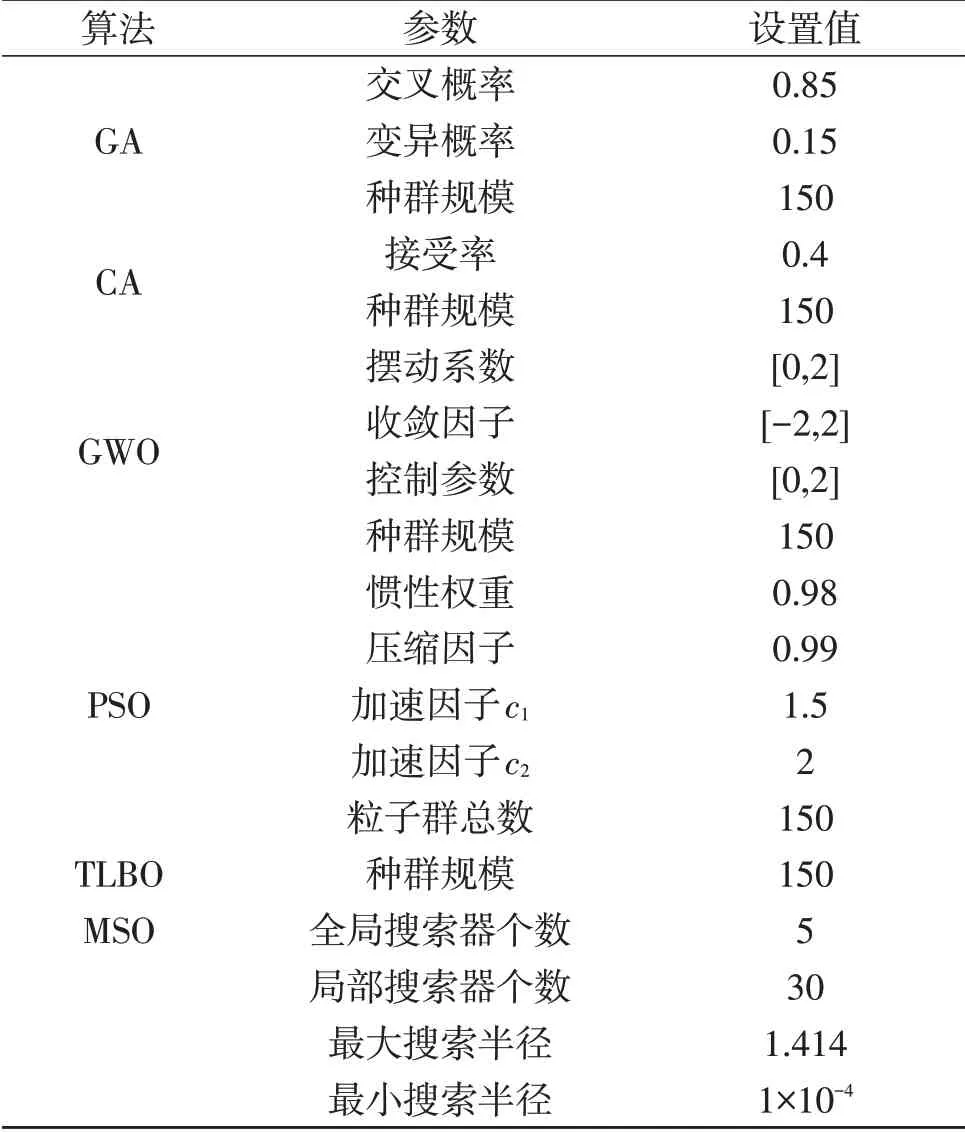
表3 对比算法参数设置Table 3 Comparison algorithm parameter settings
图15 所示为断面62 信息矩阵的收敛曲线,进行信息迁移后,就可以快速获得最优的信息矩阵,TMSQ 的优化速度得到了极大的提升,20 步内即可完成收敛,相比图13 未进行信息迁移,其效率提高了6 倍左右,并且能够有效地避免负迁移的现象出现。针对断面62,7 种算法分别对目标函数进行优化,其收敛曲线见图16。TMSQ 在迭代30 步后就开始收敛,优化速度仅次于TLBO,但是其所得的目标函数值远远小于TLBO,并且在7 种算法中收敛结果最优,各算法96 个断面运行30 次,结果统计见表4。

图15 断面62信息矩阵的收敛曲线Fig.15 Convergence curve of information matrix of section 62
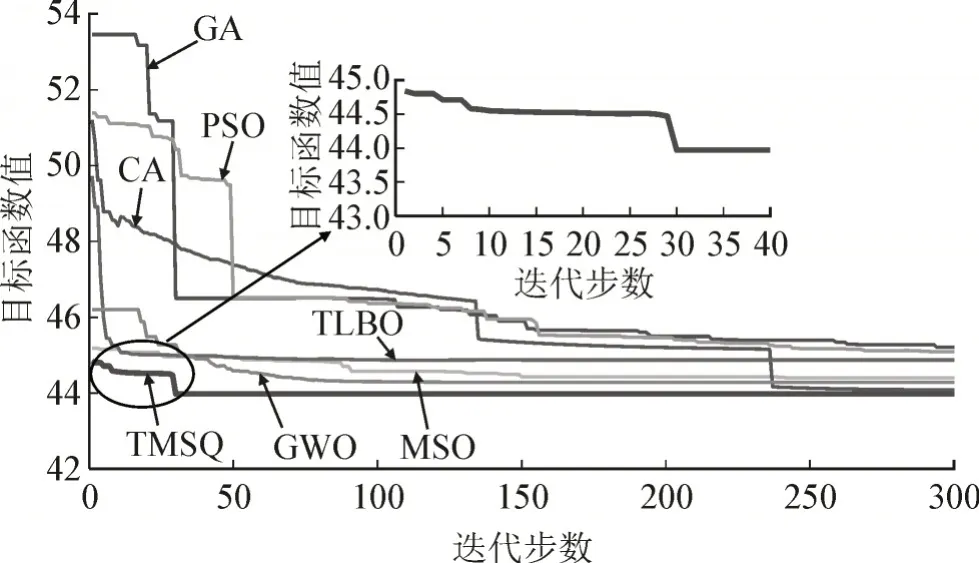
图16 7种算法目标函数收敛曲线对比图Fig.16 Comparison of convergence curves of objective functions of seven algorithms
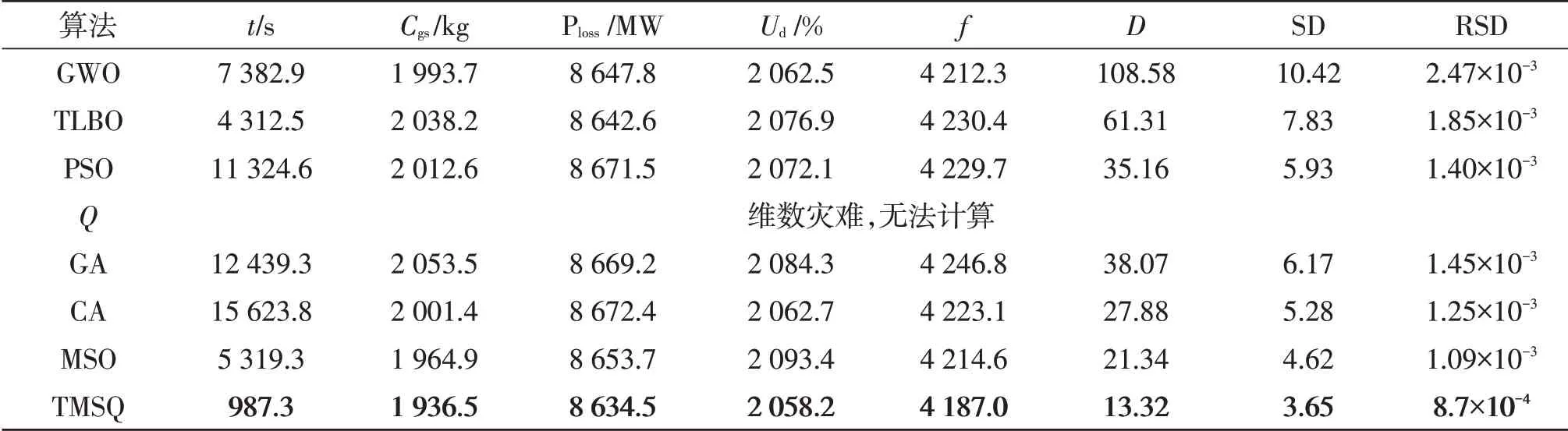
表4 算法96个断面运行30次结果统计Table 4 Results statistics of 96 sections operating for 30 times in each algorithm
5 结语
本文提出了迁移多搜索器Q学习算法,并将其应用到碳-能复合流无功优化应用场景中去。在IEEE 118 标准节点系统进行了仿真验证,同时对比灰狼进化算法、文化算法、教与学优化算法等智能算法,结果表明,所提的算法均能明显在提升收敛速度的同时求得最优解,实现电力系统经济、低碳、安全运行。
通过算例仿真,可以得到以下结论:
1)以Q学习技术的信息矩阵为载体,迁移多搜索器Q学习算法的各个搜索器对搜索器所处的环境进行交互,并将各个搜索器获得的及时奖励进行评估,用来更新其搜索器的信息矩阵,最终获得搜索器的最优信息矩阵。
2)在处理连续变量的优化及信息储存方面,采用二进制编码将连续的变量离散化处理,并且通过相互联系的状态-动作链将高维的动作空间划分成低维的动作空间,能有效地避免状态-动作空间“维度灾难”。
3)在对信息进行非线性迁移的过程中,引入了长短期记忆神经网络技术实现了多个历史任务信息矩阵的网络存储,然后高精度地预测新任务最优信息矩阵,充分利用历史优化信息提高寻优速度。
