基于自适应组合模型的超短期风速预测

关永锋，喻 敏，胡 佳

基于自适应组合模型的超短期风速预测

关永锋1,2，喻 敏1,2，胡 佳1,2

(1.冶金工业过程系统科学湖北省重点实验室(武汉科技大学)，湖北 武汉 430081；2.武汉科技大学理学院，湖北 武汉 430065)

风电场的风速预测对电力系统的稳定及安全运行有着重大的影响。考虑到风速序列具有间歇性和随机性等特征，提出一种基于参数优化的变分模态分解及极限学习机的组合模型，将其用于超短期风速预测。首先，采用变分模态分解算法将风速序列分解为一系列的平稳分量。以正交性为适应度函数，利用网格优化算法搜索变分模态分解的关键参数值——分解层数和惩罚因子，确保分解出来各模态分量之间的信息正交性，抑制耦合分量的产生。然后，利用极限学习机对各分量进行预测。针对极限学习机预测不稳定的问题，采用粒子群算法对其初始权值及阈值进行参数优化，对于该模型的输入维数则运用自回归差分移动平均模型的定阶结果进行自适应确定。最后，叠加各分量的预测值作为最终的预测结果。实验结果表明，所提出的组合模型在预测精度上显著优于其他基准模型。

参数优化的变分模态分解；自回归差分移动平均模型；粒子群优化算法；极限学习机；超短期风速预测

0 引言

随着石油、天然气等传统资源的枯竭和环境污染等问题日益突出，风电作为一种技术较为成熟的清洁发电方式，在电网中的渗透率不断提高[1-3]。然而，由于风速的随机性和间歇性，大规模接入风电会导致电力系统中的电压产生频繁波动而破坏其稳定性[4-5]。准确地预测风速可以有效地指导风机功率控制，也是保证大规模风电并网的内在要求和基本任务[6-8]。因此，提高风速的预测精度成为提升风电运行控制水平的一个主要途径。

准确地对风速进行超短期预测，可以减少电力系统备用容量，提高风电穿透功率极限，使电力市场经济效益最大化[9-10]。目前，常用的超短期风速预测模型包括统计模型[11-12]、人工神经网络模型[13-14]、组合模型[15-18]以及考虑空间相关性或季风特性的模型[19-22]。以自回归移动平均模型为代表的统计模型能有效刻画风速序列的走势和周期波动，但这类模型要求数据满足平稳性条件，强行将其用于不平稳数据的预测会导致结果出现伪回归；以反向传播神经网络模型为代表的人工神经网络模型具有较强的非线性映射能力及学习能力，但此类模型参数较多，易产生过拟合现象；组合模型通过引入多尺度分解的方法对原始风速序列进行预处理，然后采用单一预测模型进行预测，此类方法能有效把握风速数据的变化规律，具有较高的预测精度。但由于风速序列自身所具有的非线性、非平稳特性，导致分解出来的分量出现模态混叠现象，影响了模型的预测精度；空间相关模型依据风电场周边站点的风速数据来预测未来风速，对数据样本的依赖性较小，能充分考虑地理位置对风速预测的影响，特别地，在存在季风气候的地区[22]，可进一步利用季风特性对空间相关模型进行改进，但此类模型受测风站位置、风向变化的影响较大。

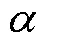
1 研究方法

1.1 变分模型分解

变分模态分解算法[27-28]是K.Dragomiretskiy和D.Zosso提出的一种新型时频分析方法。不同于传统的EMD算法，VMD是一种非递归分解方法，其采用迭代的形式求解变分模型的最优解，进而确定每个IMF分量的中心频率及带宽，自适应地分离出若干个具有不同频率成分的模态分量，具有较好的采样效应和噪声鲁棒性，在风速预测领域有广泛的应用。

该算法可分为构造变分问题和求解变分问题两个过程。所构造的变分问题可以表述为

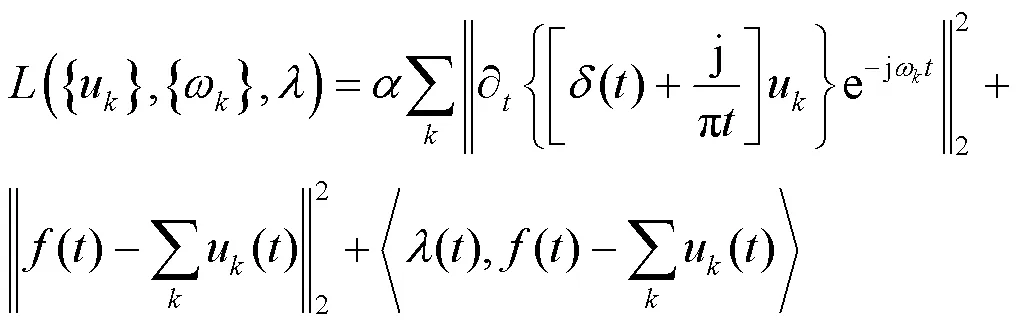
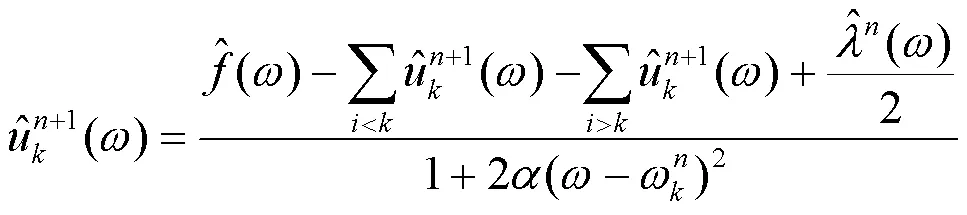
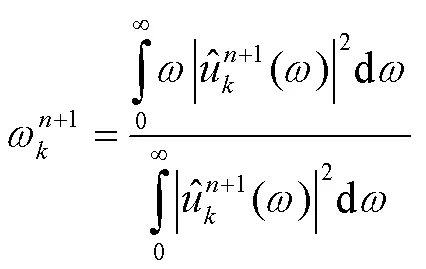
当满足式(6)的收敛条件时，迭代更新停止，输出各模态子序列。

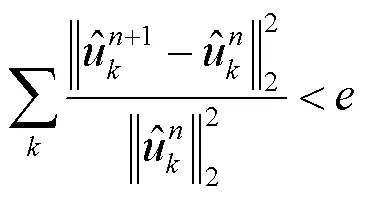
1.2 自回归差分移动平均模型

自回归差分移动平均模型是由Box和Jenkins提出的一种用于处理非平稳时间序列的模型。ARIMA模型是将非平稳数据转换成平稳数据后，对因变量的滞后值及随机误差项的现值和滞后值进行回归所建立的模型，简记为ARIMA(,,)，其数学表达式为

对于ARIMA模型的定阶，可计算其各阶数下相应的AIC(Akaike Information Criterion)值，然后寻找AIC的极小值，极小值所对应的阶数即为该模型的最佳阶数，由此可建立ARIMA模型。AIC准则是衡量ARIMA模型拟合优良性的一种标准。

1.3 极限学习机

极限学习机是一种基于单隐含层前馈神经网络的改进算法，与传统神经网络模型相比，ELM结构简单，不易陷入局部最优，具有学习速度快、泛化能力好等优点。

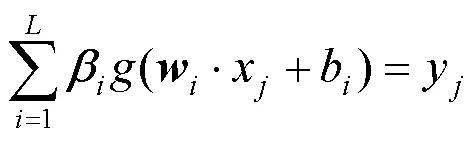
对应的矩阵形式为

其解为

2 自适应风速超短期预测模型

2.1 网格搜索优化的变分模态分解

由VMD计算过程可以发现，在运用该算法时需人为确定两个关键参数：分解层数和惩罚因子。前人在运用该算法时大都只针对分解层数的选取进行讨论，如采用中心频率法[9]，对于惩罚因子则采用的是默认值。但是，惩罚因子对VMD分解结果的影响也是不可忽略的，仅仅考虑分解层数的选取是不够的，因此，本文提出将GS算法用于VMD的参数优化中，具体步骤如下所述。

1) 确定分解层数和惩罚因子的搜索步长及搜索范围；

3) 在每一组参数组合下，对风速数据进行VMD分解，计算各模态分量间的正交性(Index of Orthogonality, IO)，如式(14)。

4) 选取正交性最小时所对应的参数组合为最优参数值。

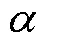
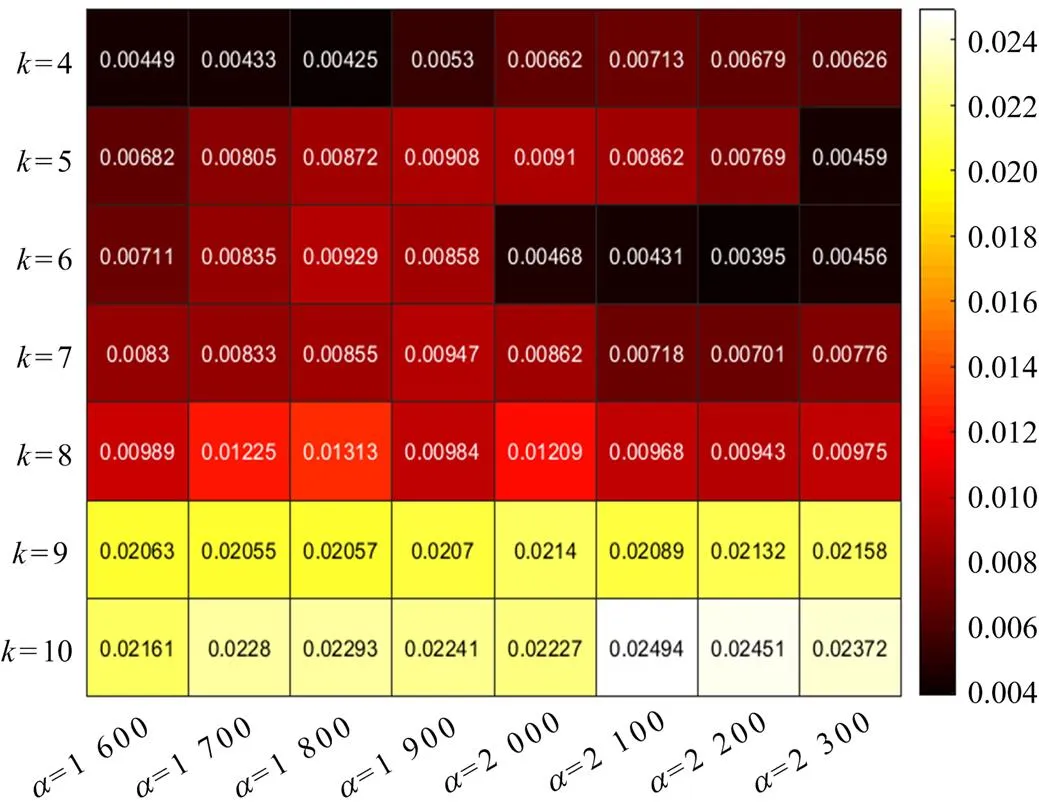
图1 VMD网格搜索优化结果可视化

2.2 ARIMA模型确定网络输入维数

在建立神经网络模型的时候，需要先确定网络的拓扑结构，其中网络隐含层神经元个数通常采用公式经验法[29]、误差迭代寻优法[30]来确定；对于时间序列预测问题，网络的输出维数通常设定为1。而对于网络输入维数的确定方法，则常采用相空间重构[30]或偏向关函数[31](Partial Autocorrelation Function, PACF)，但这两种方法均存在一些问题。如前者计算过程较为复杂，需要耗费较多时间；而后者需要通过人为观察PACF图来确定维数，缺乏自适应性。因此，为使确定网络输入维数的方式具备自适应性且无需耗费过多的时间，本文提出运用ARIMA模型来确定神经网络的输入维数。

对三组风速数据经GS-VMD分解后的各分量依次建立ARIMA模型，模型参数如表1所示。以10 min风速数据的IMF3为例说明本文预测模型输入变量的构成。如图2所示，本文模型采用超前1步预测的策略，以连续4个时刻的历史风速值作为模型的输入预测下一时刻的风速值，图中变量即为模型的预测值。

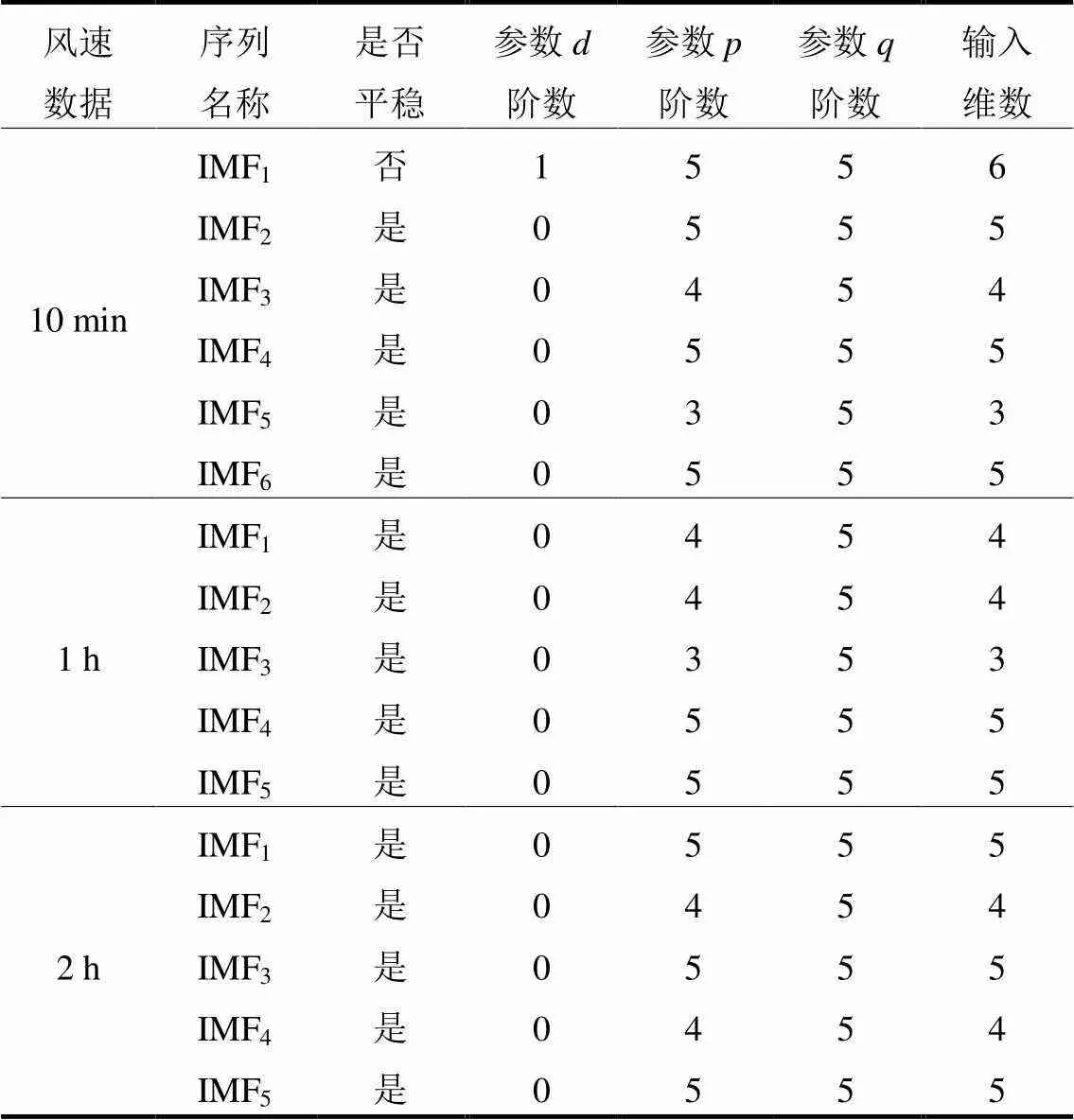
表1 各序列ARIMA建模结果及网络输入维数的确定

图2 预测模型的输入变量构成

2.3 基于粒子群优化的极限学习机

粒子群优化算法是一种群智能优化算法，基于“种群”和“进化”的概念，通过个体间的协作与竞争，实现复杂空间最优解的搜索。

由于初始连接权值和偏置值随机设定所带来的偏差，极限学习机常常出现预测结果不稳定的问题[32-33]。为提高ELM模型的鲁棒性及预测准确性，本文采用粒子群算法对ELM模型中的初始参数进行优化。PSO-ELM建模步骤如下。

1) 载入风速数据。对数据进行归一化处理，并区分训练集以及测试集。

2) 确定PSO-ELM模型的拓扑结构。首先，建立风速序列的ARIMA模型，根据AIC值最小原则选取最佳的定阶参数作为网络的输入维数，建立一个具有个输入节点、1个输出节点的网络。而后，通过迭代寻优的方式确定网络最佳隐含层个数，对采样间隔为10 min的风速数据进行仿真实验，其寻优结果如图3所示，可知当迭代次数为22时，网络的误差最小，因此可确定隐含层神经元个数为22。网络激活函数选择的是Sigmoid函数。

图3 PSO-ELM模型隐含层神经元个数的确定

5) 判断是否达到最大迭代次数或最小误差，若达到则迭代停止，否则将继续迭代。

6) 将优化后得到的初始权值和偏置值代入ELM模型的训练中，在模型训练好后，将测试集代入模型进行预测并计算预测误差。

2.4 算法流程

本文遵循“分解-组合”的思想，提出一种基于GS-VMD、ARIMA和PSO-ELM的自适应风速超短期预测组合模型。如图4所示，该模型的预测流程如下：

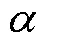
2) 依次对各IMF分量建立ARIMA模型，以AIC最小准则确定各分量ARIMA模型的最优参数，并以此确定网络的输入维数。

3) 对确定好输入维数的各IMF分量，采用PSO-ELM模型依次进行预测，获得每个分量的预测值；

4) 叠加各个分量的预测值获取最终的风速预测值。

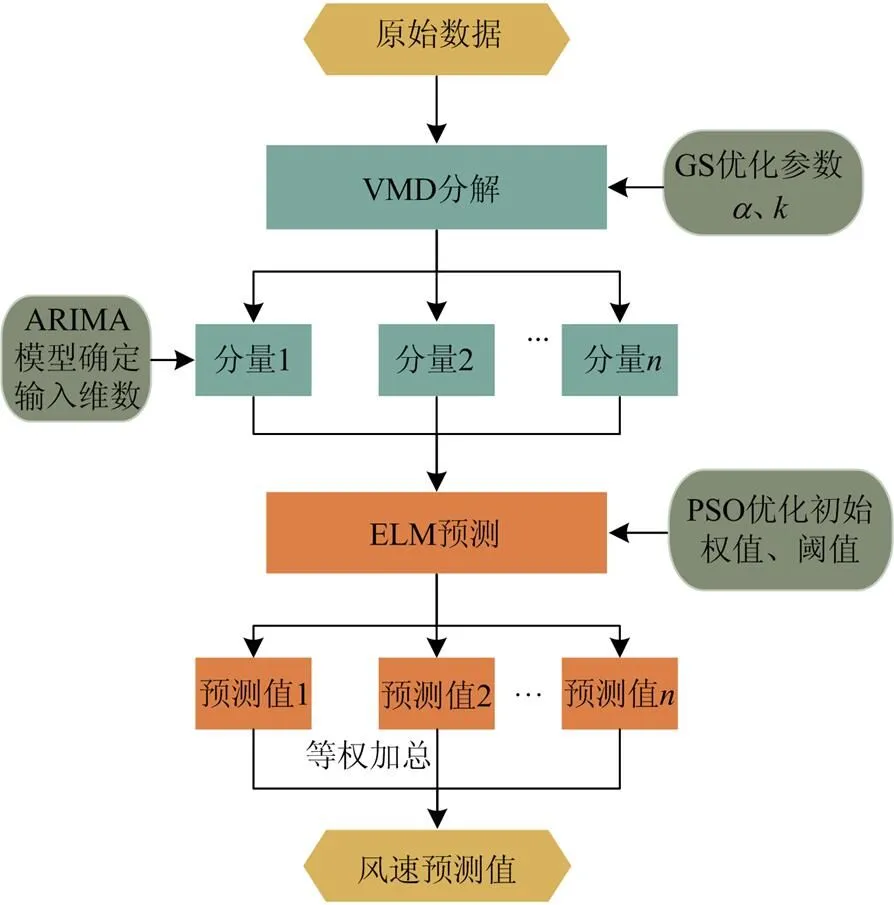
图4 本文模型的框架

2.5 评价指标

为分析各模型风速预测值与实际值之间的误差，选取平均误差(Mean Error, ME)、平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、均方根误差(Root Mean Square Error, RMSE)、可决系数2(Coefficient of determination, R-square) 4个指标对模型的预测精度以及拟合优度进行评价，计算公式为

3 实验结果分析

从天气预报的实践看，仅利用风速历史数据进行统计学预报，对未来风速预报的提前时间是有限的，因此，为说明本文模型对于风速预报提前时间的定位能力，选取西班牙某风电场2020年2月采样间隔为10 min以及3月采样间隔为1 h、2 h的三组风速数据作为研究对象进行超前一步风速预测研究。其中，采样间隔为10 min的风速数据缺失一个样本，采用临近点线性趋势插值法对该缺失数据进行填充以获取完整的样本。表2给出了三组风速数据的描述性统计分析结果，同时，将三组风速数据分别划分为训练集和测试集，分别用于模型的训练和预测，如图5所示。结合图表可发现三组风速序列波动较为剧烈，均具有明显的非线性非平稳特征。

为说明本文GS-VMD-ARIMA-PSO-ELM组合模型的预测效果，选取以反向传播神经网络模型为代表的机器学习模型、以长短时记忆网络模型(Long Short-Term Memory, LSTM)为代表的深度学习模型、以ARMA模型为代表的传统统计模型以及本文所用到的ELM模型及其改进模型作为单一基准模型，另选取引入经验模态分解、集合经验模态分解两种多尺度分解方法的复合模型作为组合基准模型，与本文模型进行对比，分别进行提前10 min、1 h、2 h的单步预测，预测效果如图6所示，同时表3给出了各模型预测效果的评价指标结果。

表2 描述性统计分析

图5 西班牙风电场实测风速数据

图6 各模型的预测结果

从单一模型角度来看，与BP、ARMA、LSTM模型相比，ELM模型具有更好的预测效果，同时，在引入粒子群优化算法后，该模型的预测效果有了进一步提高。在拟合优度方面，相较于单一模型中拟合优度较低的ARMA模型来说，PSO-ELM模型的2提高了6.36%～9.52%；在预测精度方面，相较于单一模型中、这三项指标都较大的BP模型来说，PSO-ELM模型的减小了1.78%～5.59%，减小了0.41 m/s左右，减小了0.20 m/s左右。这说明了利用ELM学习速度快以及PSO启发式全局寻优的优点能有效提高风速预测的效果。

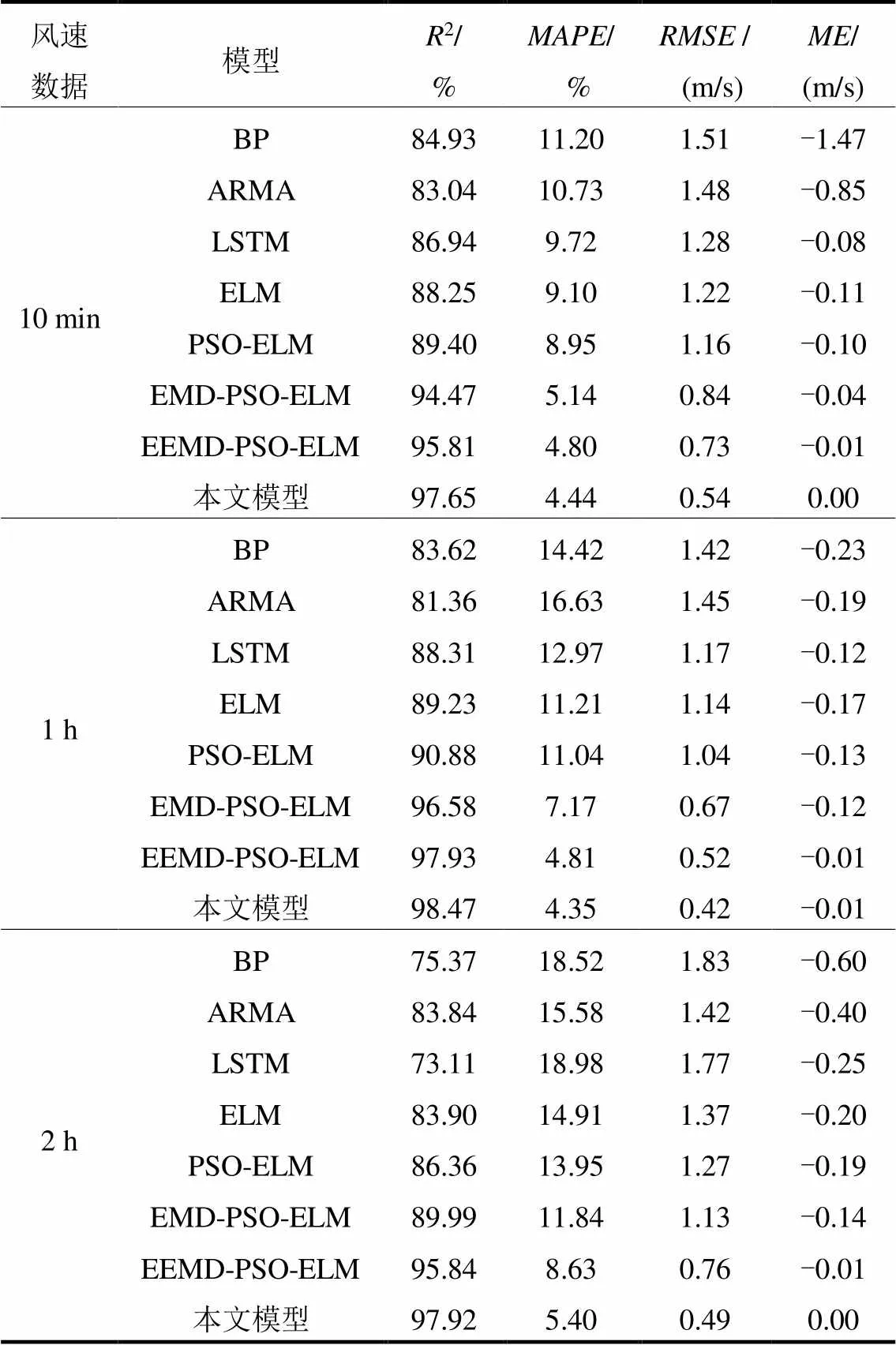
表3 各模型的误差评价

从组合模型角度来看，由于单一模型缺乏平稳化预处理过程，致使其无法学习到具有强随机性、非线性的风速数据的内部规律，预测效果明显差于组合模型，这说明了在引入多尺度分解的信号处理算法后，能有效降低原始风速序列的非平稳性和间歇性，预测结果更加平滑，能较好地克服样本波动对预测精度的影响。进一步比较三种组合模型的预测效果，可以发现，在拟合优度方面，相较于其余两个组合模型中拟合优度较低的EMD-PSO-ELM模型来说，本文模型的2提高了1.89%～3.18%；在预测精度方面，相较于其余两个组合模型中值、值和值都较大的EMD-PSO-ELM模型来说，本文模型的减小了0.70%～2.82%，减少了0.30 m/s左右，减少了0.14 m/s左右。这说明了GS-VMD算法具有较好的降噪能力，能更好地对原始风速序列进行平稳化处理。

同时，对各模型的残差序列进行分析，结果如图7所示，可发现本文模型的残差序列基本在0值附近平稳波动，离群点较少，总体效果好于其他7个基准模型。

图7 各模型的残差分析

综上，本文所提出的GS-VMD-ARIMA-PSO- ELM模型具有较高的预测精度和拟合优度，不仅通过自适应分解对原始风速数据进行平稳化处理，同时也能准确把握分解后各模态分量的变化规律，预测未来提前时间分别可达到10 min、1 h和2 h，符合实际风力发电系统的预测需求。

4 结论

本文将GS-VMD算法、ARIMA模型和PSO- ELM模型相结合，遵循“分解-组合”的思路，提出了一种用于超短期风速预测的自适应模型。通过实例分析，得出以下结论：

2) 与传统的相空间重构法和PACF法相比，本文运用ARIMA模型来确定神经网络的输入维数可以提高模型的自适应能力，节省计算时间。

3) 运用极限学习机模型能加快风速预测的速度，在引入粒子群算法优化其初始权值和阈值后，有效解决了该模型预测结果不稳定的问题，优化得到的参数更优良，有效提高了预测的准确性及鲁棒性。

[1] 孙舶皓, 汤涌, 叶林, 等.基于分层分布式模型预测控制的多时空尺度协调风电集群综合频率控制策略[J].中国电机工程学报, 2019, 39(1): 155-167, 330.

SU Bohao, TANG Yong, YE Lin, et al.Integrated frequency control strategy for wind power cluster with multiple temporal-spatial scale coordination based on H-DMPC[J].Proceedings of the CSEE, 2019, 39(1): 155-167, 330.

[2] 禹海峰, 潘力强, 吴亚茹, 等.储能提升含高比例风电电力系统可靠性分析[J].电网与清洁能源, 2020, 36(6): 92-98.

YU Haifeng, PAN Liqiang, WU Yaru, et al.Analysis of energy storage improving the reliability of power system with high proportional wind power[J].Power System and Clean Energy, 2020, 36(6): 92-98.

[3] 李炅聪, 施嘉昊, 武庆, 等.含风电接入的电力系统脆弱性分析与量化评估[J].电网与清洁能源, 2020, 36(1): 46-54.

LI Jiongcong, SHI Jiahao, WU Qing, et al.Vulnerability analysis and quantitative evaluation of the power system containing wind power[J].Power System and Clean Energy, 2020, 36(1): 46-54.

[4] JUNG C, TAUBERT D, SCHINDLER D.The temporal variability of global wind energy long-term trends and inter-annual variability[J].Energy Conversion and Management, 2019, 188(5): 462-472.

[5] QIAN Z, PEI Y, ZAREIPOUR H, et al.A review and discussion of decomposition-based hybrid models for wind energy forecasting applications[J].Applied Energy, 2019, 235(2): 939-953.

[6] 陈金富, 朱乔木, 石东源, 等.利用时空相关性的多位置多步风速预测模型[J].中国电机工程学报, 2019, 39(7): 2093-2106.

CHEN Jinfu, ZHU Qiaomu, SHI Dongyuan, et al.A multi-step wind speed prediction model for multiple sites leveraging spatio-temporal correlation[J].Proceedings of the CSEE, 2019, 39(7): 2093-2106.

[7] 王鑫, 李慧, 叶林, 等.考虑风速波动特性的VMD-GRU短期风电功率预测[J].电力科学与技术学报, 2021, 36(4): 20-28.

WANG Xin, LI Hui, YE Lin, et al.VMD-GRU based shortterm wind power forecast considering wind speed fluctuation characteristics[J].Journal of Electric Power Science and Technology, 2021, 36(4): 20-28.

[8] 张帅可, 罗萍萍.基于混合分布模型的风电功率超短期预测误差分析[J].电力科学与技术学报, 2020, 35(5): 111-118.

ZHANG Shuaike, LUO Pingping.Ultra short-time prediction error analysis of wind power based on mixed distribution model[J].Journal of Electric Power Science and Technology, 2020, 35(5): 111-118.

[9] JUNG J, BROADWATERR P.Current status and future advances for wind speed and power forecasting[J].Renewable & Sustainable Energy Reviews, 2014, 31(3): 762-777.

[10]王俊, 李霞, 周昔东, 等.基于VMD和LSTM的超短期风速预测[J].电力系统保护与控制, 2020, 48(11): 45-52.

WANG Jun, LI Xia, ZHOU Xidong, et al.Ultra-short term wind speed prediction based on VMD and LSTM[J].Power System Protection and Control, 2020, 48(11): 45-52.

[11] AASIM, SINGH S, MOHAPATRA A.Repeated wavelet transform based ARIMA model for very short-term wind speed forecasting[J].Renewable Energy, 2019, 136(6): 758-768.

[12]刘帅, 朱永利, 张科, 等.基于误差修正ARMA-GARCH模型的短期风电功率预测[J].太阳能学报, 2020, 41(10): 268-275.

LIU Shuai, ZHU Yongli, ZHANG Ke, et al.Short-term wind power forecasting based on error correction ARMA-GARCH model[J].Acta Energiae Solaris Sinica, 2020, 41(10): 268-275.

[13]杨茂, 周宜.计及风电场状态的风电功率超短期预测[J].中国电机工程学报, 2019, 39(5): 1259-1268.

YANG Mao, ZHOU Yi.Ultra-short-term prediction of wind power considering wind farm status[J].Proceedings of the CSEE, 2019, 39(5): 1259-1268.

[14] MADHIARASAN M.Accurate prediction of different forecast horizons wind speed using a recursive radial basis function neural network[J].Protection and Control of Modern Power Systems, 2020, 22(5): 2-9.

[15] 韩宏志, 唐振浩.基于CEEMDAN与回声状态网络的风速预测方法[J].电力系统保护与控制, 2020, 48(12): 90-96.

HAN Hongzhi, TANG Zhenhao.Wind speed prediction method based on CEEMDAN and ESN[J].Power System Protection and Control, 2020, 48(12): 90-96.

[16] 王韶, 杨江平, 李逢兵, 等.基于经验模式分解和神经网络的短期风速组合预测[J].电力系统保护与控制, 2012, 40(10): 6-11, 18.

WANG Shao, YANG Jiangping, LI Fengbing, et al.Short-term wind speed forecasting based on EMD and ANN[J].Power System Protection and Control, 2012, 40(10): 6-11, 18.

[17] JASEENA K, KOVOOR B.Decomposition-based hybrid wind speed forecasting model using deep bidirectional LSTM networks[J].Energy Conversion and Management, 2021, 234(6): 113944.

[18] LIU Mingde, DING Lin, BAI Yulong.Application of hybrid model based on empirical mode decomposition, novel recurrent neural networks and the ARIMA to wind speed prediction[J].Energy Conversion and Management, 2021, 233(2).

[19] YANG B, ZHONG L, WANG J, et al.State-of-the-art one-stop handbook on wind forecasting technologies: an overview of classifications, methodologies, and analysis[J].Journal of Cleaner Production, 2020, 283(6).

[20] AHMED A, KHALID M.A review on the selected applications of forecasting models in renewable power systems[J].Renewable and Sustainable Energy Reviews, 2019, 100: 9-21.

[21] 薛禹胜, 陈宁, 王树民, 等.关于利用空间相关性预测风速的评述[J].电力系统自动化, 2017, 41(10): 161-169.

XUE Yusheng, CHEN Ning, WANG Shumin, et al.Review on wind speed prediction based on spatial correlation[J].Automation of Electric Power Systems, 2017, 41(10): 161-169.

[22] 杨正瓴, 冯勇, 熊定方, 等.基于季风特性改进风电功率预测的研究展望[J].智能电网, 2015, 3(1): 1-7.

YANG Zhengling, FENG Yong, XIONG Dingfang, et al.Research prospects of improvement in wind power forecasting based on characteristics of monsoons[J].Smart Grid, 2015, 3(1): 1-7.

[23] 黄进.基于极值偏移优化的ARIMA的短期风速预测[J].制造业自动化, 2018, 40(1): 79-85.

HUANG Jin.The shifting of extreme short-term wind speed prediction based on the optimization of ARIMA[J].Manufacturing Automation, 2018, 40(1): 79-85.

[24] 潘震, 黄国勇, 吴漫.基于参数优化VMD和增强多尺度排列熵的单向阀故障诊断[J].振动与冲击, 2020, 39(15): 118-125.

PAN Zhen, HUANG Guoyong, WU Man.Fault diagnosis of one-way valve based on parameter optimization VMD and enhanced multi-scale arrangement entropy[J].Vibration and Impact, 2020, 39(15): 118-125.

[25] 徐波, 黎会鹏, 周凤星, 等.基于自适应CEEMD的非平稳信号分析方法[J].振动、测试与诊断, 2020, 40(1): 54-61, 203.

XU Bo, LI Huipeng, ZHOU Fengxing, et al.Non-stationary signal analysis method based on adaptive CEEMD[J].Vibration, Testing and Diagnosis, 2020, 40(1): 54-61, 203.

[26] 李兵, 刘明亮, 杨平.EWT与GS-SVM在断路器机械故障诊断中的应用[J].哈尔滨工程大学学报, 2018, 39(8): 1422-1430.

LI Bing, LIU Mingliang, YANG Ping.Application of EWT and GS-SVM in mechanical fault diagnosis of circuit breakers[J].Journal of Harbin Engineering University, 2018, 39(8): 1422-1430.

[27] DRAGOMIRETSKIY K, ZOSSO D.Variational mode decomposition[J].IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.

[28] 许子非, 岳敏楠, 李春.优化递归变分模态分解及其在非线性信号处理中的应用[J].物理学报, 2019, 68(23): 292-305.

XU Zifei, YUE Minnan, LI Chun.Application of the proposed optimized recursive variational mode decomposition in nonlinear decomposition[J].Acta Physica Sinica, 2019, 68(23): 292-305.

[29] 卢格宇.CEEMD下神经网络的短期风速预测研究[D].长沙: 长沙理工大学, 2017.

LU Geyu.Short-term wind speed prediction of neural networks under CEEMD[D].Changsha: Changsha University of Science and Technology, 2017.

[30] 苏盈盈, 李翠英, 王晓峰, 等.风电场短期风速的C-C和ELM快速预测方法[J].电力系统及其自动化学报, 2019, 31(7): 76-80, 87.

SU Yingying, LI Cuiying, WANG Xiaofeng, et al.Short-term wind speed C-C and ELM rapid prediction method for wind farms[J].Proceedings of the CSU-EPSA, 2019, 31(7): 76-80, 87.

[31]陈慧丽.基于混合优化模型风速预测的研究[D].兰州:兰州大学, 2020.

CHEN Huili.Research on wind speed prediction based on hybrid optimization model[D].Lanzhou: Lanzhou University, 2020.

[32] 王浩, 王艳, 纪志成.基于SAIGM-KELM的短期风电功率预测[J].电力系统保护与控制, 2020, 48(18): 78-87.

WANG Hao, WANG Yan, JI Zhicheng.Short-term wind power forecasting based on SAIGM-KELM[J].Power System Protection and Control, 2020, 48(18): 78-87.

[33] 徐睿, 梁循, 齐金山, 等.极限学习机前沿进展与趋势[J].计算机学报, 2019, 42(7): 1640-1670.

XU Rui, LIANG Xun, QI Jinshan, et al.Advances and trends in extreme learing machine[J].Chinese Journal of Computers, 2019, 42(7): 1640-1670.

Ultra-short-term wind speed prediction based on an adaptive integrated model

GUAN Yongfeng1, 2, YU Min1,2, HU Jia1,2

(1.Hubei Province Key Laboratory of Systems Science in Metallurgical Process, Wuhan University of Science and Technology, Wuhan 430081, China; 2.College of Science, Wuhan University of Science and Technology, Wuhan 430065, China)

Wind speed prediction has a significant impact on the stable and safe operation of a power system.According to the intermittent and random nature of wind speed, an integrated model of variational modal decomposition (VMD) based on grid search optimization algorithm (GS) and PSO-ELM is proposed for ultra-short-term wind speed prediction.First, the VMD is used to decompose wind speed sequence into a series of sub-sequences.By taking the orthogonality as the fitness function, the GS is used to search the key parameters of VMD adaptively, including the number of decomposed layers and a penalty factor.The purpose is to ensure information orthogonality between each component and to suppress coupling components.Then, the extreme learning machine (ELM) method is used to predict each sub-sequence.Given the unstable prediction of this model, particle swarm algorithm (PSO) is used to optimize the parameters of the initial weight and threshold, and the input dimension of each sub-sequence is determined adaptively by using the auto-regressive integrated moving average model (ARIMA).Finally, the predicted results of each sub-sequence are superimposed to obtain the final predicted wind speed.The result shows that the proposed integrated model is remarkably superior to all considered benchmark models in prediction accuracy.This work is supported by the National Natural Science Foundation of China (No.51877161).

parameter optimized variational modal decomposition; ARIMA; PSO; ELM; ultra-short-term wind speed prediction

10.19783/j.cnki.pspc.210446

2021-04-20；

2021-08-28

关永锋(1994—)，男，硕士研究生，研究方向为风电场风速与风电功率预测；E-mail: chokfengguan@qq.com

喻 敏(1975—)，女，通信作者，博士，讲师，研究方向为电能质量、风速风功率预测、分形和小波等。E-mail: yufeng3378@163.com

国家自然科学基金项目资助(51877161)；湖北省教育厅科研计划指导项目资助(2018006)；冶金工业过程系统科学湖北省重点实验室开放基金资助(Y202007)

(编辑 葛艳娜)