基于统计抽样的压水堆燃料组件性能分析不确定度量化研究
2022-03-02邹晓阳曹良志刘宙宇吴宏春
邹晓阳,曹良志,刘宙宇,吴宏春
(西安交通大学 核科学与技术学院,陕西 西安 710049)
反应堆的设计和安全运行离不开高精度、高分辨率的模拟仿真计算程序,随着计算方法的发展和计算机硬件的进步,高保真数值反应堆技术成为研究热点。但由于客观世界的复杂性和人类认知水平的限制,任何测量和数学-物理建模过程都存在不确定性,因此模拟仿真计算结果需要提供相应的不确定度作为置信区间,以满足数值反应堆技术中高置信度的要求。
为推动反应堆系统不确定度量化研究的发展,经济合作组织核能局(OECD/NEA)成立了不确定性分析专家组(UAM),并发布了针对轻水堆系统不确定度量化的基准题UAM-LWRs。该基准题将轻水堆系统的不确定度量化分为3个研究阶段:中子学阶段[1]、堆芯阶段[2]和系统阶段[3]。中子学阶段主要研究核数据的不确定度在稳态中子学计算中的传递过程,核数据的不确定度从评价核数据库(ENDF)传递给多群微观截面,而后传递给宏观少群截面以及稳态堆芯计算的关键参数。堆芯阶段包括燃料性能分析、与时间相关的中子学计算、组件热工水力计算3个独立的物理过程。系统阶段包括多物理耦合计算,并最终给出最佳估算加不确定度结果(BEPU)。将BEPU与保守计算结果进行对比,能进一步确保反应堆系统的安全性并减小安全裕量,提高经济性。
因此,针对每种物理场,分别量化其输入输出参数的不确定度,对于后续量化复杂系统多物理耦合过程的不确定度具有重要意义。本文利用西安交通大学自主开发的不确定度量化程序NECP-UNICORN[4-5],采用面向协方差矩阵的样本变换方法(COST)[6]实现核数据的相关性抽样,针对UAM-LWRs不确定度量化基准题中的TMI-1压水堆燃料组件,分别对燃料性能分析、燃耗计算以及热工水力分析过程进行不确定度量化。
1 不确定度来源
1.1 燃料性能分析
燃料性能分析程序通过模拟燃料的行为评估其性能、模拟所设计的实验过程并对实验现象进行解释、对正常运行或事故工况进行安全分析。由于燃料性能分析过程涉及众多输入参数,燃料性能分析程序计算结果的不确定度主要来源于以下几个方面:1)边界条件的不确定度,包括系统压力、冷却剂流量、系统功率、入口冷却剂温度;2)几何的不确定度,包括包壳内径、外径、厚度、粗糙度,燃料芯块外径、富集度、粗糙度、密度和气体压力等;3)材料特性的不确定度,包括燃料热导率和包壳热导率等。
1.2 燃耗计算
燃耗计算旨在分析燃料在寿期内的运行状态以及由此产生的中子学效应,对堆芯设计和燃料管理具有重要意义。燃耗计算的不确定度主要来源于核数据的不确定度、几何参数的不确定度和数学-物理模型近似引入的不确定度。近年来,随着高保真数值反应堆技术的发展,数学-物理模型简化近似对计算结果引入的不确定度可忽略不计,而核数据以及几何参数的不确定度成为核反应堆物理计算中最重要的不确定度来源。
1)核数据不确定度
核数据来源于微观实验测量和核物理理论模型计算,并经过评估过程与宏观实验结果进行对比验证,不可避免地存在一定的不确定度。核数据的不确定度在ENDF-6格式[7]的评价核数据库中被称为协方差文件(包含核数据的方差和协方差),并定义了如下协方差文件类型:MF30(从参数协方差和灵敏度获得的数据协方差)、MF31(平均裂变中子数的数据协方差)、MF32(共振参数的数据协方差)、MF33(反应截面的数据协方差)、MF34(角分布的数据协方差)、MF35(能量分布的数据协方差)、MF40(放射性核素产生的数据协方差)。此外,还应考虑衰变常量及裂变产额的不确定度。
2)燃料组件几何参数的不确定度
燃料组件几何参数包括燃料内径和外径、包壳厚度、燃料芯块直径、燃料密度、气体压力和燃料富集度。假设所有参数都服从正态分布,且相互之间没有相关性。
1.3 热工水力分析
热工水力分析程序基于简化的守恒方程,使用数值近似方法求解不精确的数学公式。经验公式众多,且公式的有效范围有限。此外,边界条件和初始条件通常不是完全已知,这也是不确定度的来源。因此,热工水力程序计算结果的不确定度主要来源于以下几个方面:1)边界条件的不确定度,包括系统压力、冷却剂流量、系统功率、入口冷却剂温度和功率分布;2)几何的不确定度,包括燃料棒偏移和燃料棒外径;3)模型系数的不确定度,包括单相混合系数、两相混合系数、传热系数、每种流态的阻力系数、定位格架损失系数和壁面摩擦系数等。
综上所述,3种物理场的不确定度分析都考虑了几何参数/制造偏差的影响,但不同物理场考虑的参数及其不确定度不同。对于燃料性能分析过程,需要考虑对热量传导有影响的参数,如尺寸和表面粗糙度等;对于燃耗过程,需要考虑对中子行为有影响的参数,具体表现为对核子密度的影响;对于热工水力分析,需要考虑对冷却剂流道截面积有影响的参数,如直径和安装位置的偏移。
2 抽样方法
对多个独立变量抽样时,根据每个变量的概率分布函数,采用拉丁超立方体抽样进行多次独立抽样得到样本。但对于核数据,输入参数为存在相关关系的高维正态分布变量,通常需首先对同维度标准正态分布总体进行抽样,然后将其样本与转换矩阵相乘[8]。
设输入参数为X,维度为n,X的均值向量为μ=[μ1,μ2,…,μn]T,X的协方差矩阵为Σ,则X~Nn(μ,Σ);设Z~Nn(0,I)表示标准正态分布,其中I为单位矩阵,ZS为根据标准正态分布Z抽样得到的样本,维度为n×p(p为抽样样本容量)。此时利用式(1)即可得到输入参数X的样本XS:
(1)
其中:XS为输入参数X的样本集;ZS为来自标准正态分布Z~Nn(0,I)的样本;A为转换矩阵,维度为n×n;V为均值向量μ的扩展矩阵,维度为n×p。
根据2个正态分布随机变量总体X和Z之间的关系,转换矩阵A需使式(2)成立:
AAT=Σ
(2)
对于传统抽样方法,此时A可选取由Σ矩阵Cholesky分解得到的下三角矩阵,也可通过Σ矩阵特征值分解得到。传统抽样方法生成的多元正态分布样本所引入的误差来源于有限样本容量下标准正态分布样本ZS的协方差矩阵不等于单位矩阵I,意味着样本ZS无法完全描述标准正态分布总体Z。同时,可发现Σ矩阵在多输入参数情况下,通常具有稀疏、不满秩的特征。
基于上述问题,本文采用COST方法对核数据进行抽样。COST方法的关键是确定转换矩阵,使经过线性变换后的样本协方差矩阵等于给定的输入参数协方差矩阵Σ。假设根据标准正态分布抽样得到的样本ZS的协方差矩阵为I*,维度为n×n,样本的均值向量为O,其值均为0;A为可使样本协方差矩阵等于输入参数协方差矩阵Σ的转换矩阵。可以证明,无论A取何值,线性变换后样本均值向量仍为O[6]。令转换后的样本协方差矩阵等于Σ,则有:
(XS-V)(XS-V)T=(AZS)(AZS)T=
(p-1)Σ⟹AI*AT=Σ
(3)
A矩阵的构造可通过协方差矩阵Σ和I*的奇异值分解或特征值分解实现。
COST方法的转换矩阵A由来自标准正态分布的样本协方差矩阵I*和输入参数协方差矩阵Σ共同决定。该方法人为控制随机过程,克服了抽样过程中由来自标准正态分布的样本引入的误差,并可将最小样本容量确定为输入参数协方差矩阵秩的大小。因此COST方法区别于传统抽样方法,是一个定向手动挑选样本的过程,本质上已不是一个完全随机的过程,体现了确定论方法的特征和优势[9]。
3 数值结果
3.1 模型描述
本研究用于燃耗计算和热工水力分析的算例为TMI-1燃料组件,燃料棒为15×15排列,具体布置如图1所示,几何参数如表1所列,运行工况为热态满功率(HFP)。本文后续燃料性能分析、燃耗计算和热工水力分析均基于此模型。
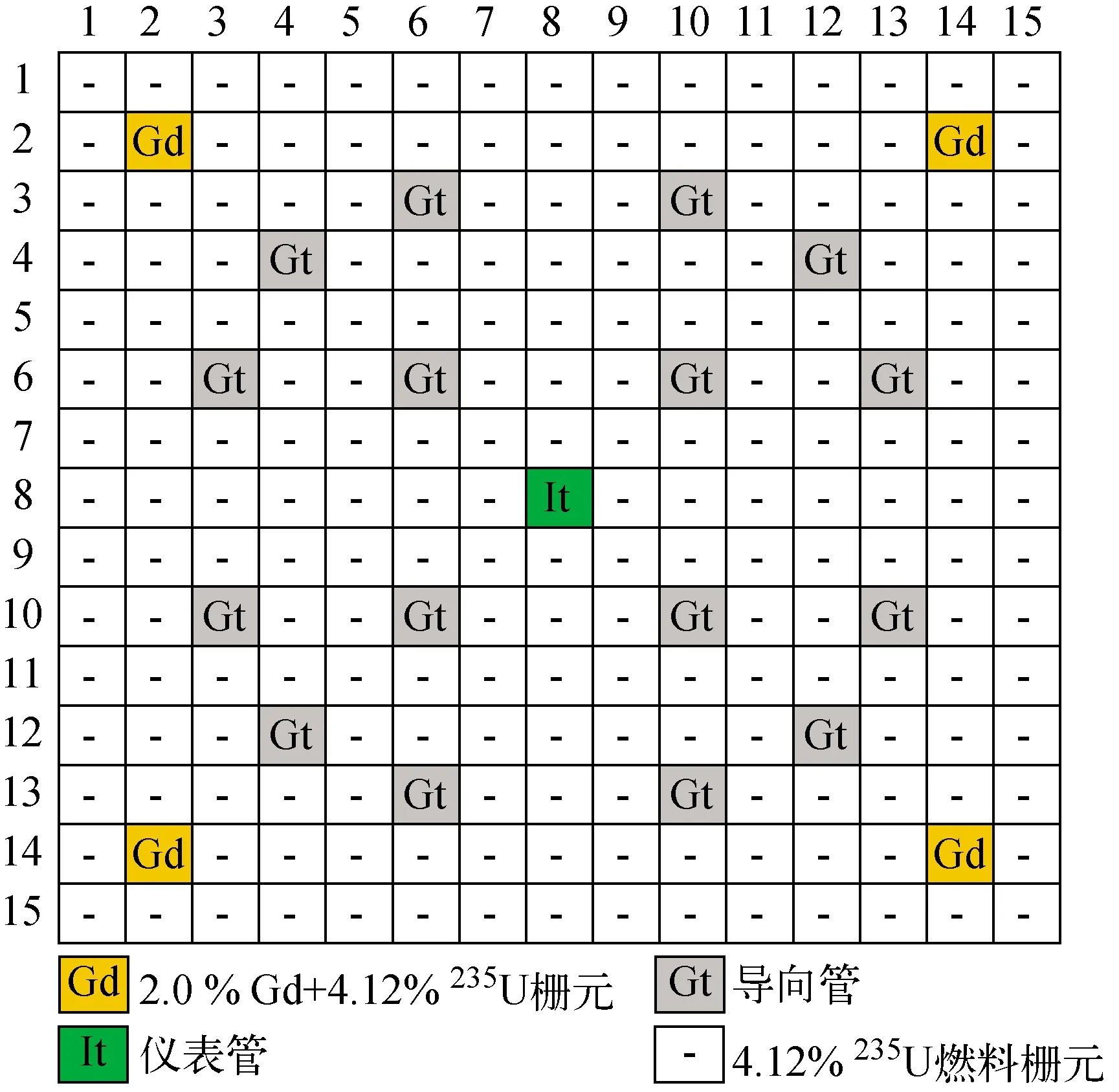
图1 TMI-1燃料组件布置

表1 TMI-1燃料组件几何参数
3.2 燃料性能分析
TMI-1燃料棒的全寿期功率历史如图2所示,寿期末的燃耗深度约为60 GW·d/tU。采用轻水堆燃料性能分析程序FEMAXI进行建模计算,与不确定度量化分析程序NECP-UNICORN进行耦合。采用统计学抽样方法,同时考虑边界条件、几何参数和材料性能等输入参数的不确定度,根据对不同样本数量统计涨落的研究[10],样本容量选为200。
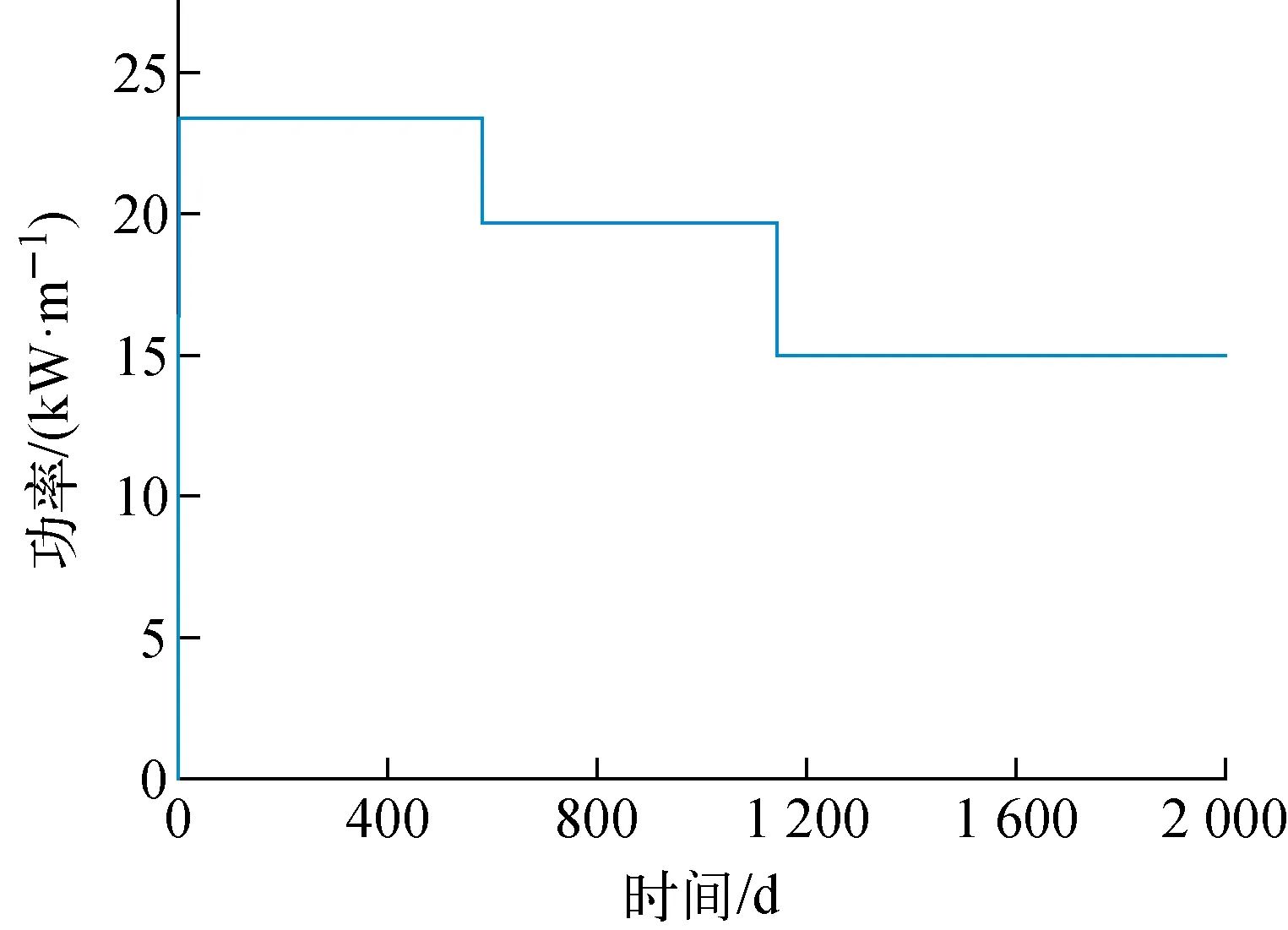
图2 TMI-1燃料栅元的功率历史
本文所研究参数的不确定度来自于UAM-LWRs Phase Ⅱ的基准题手册,需要考虑的参数及不确定度范围列于表2。

表2 燃料性能分析中输入参数的不确定度
综合考虑上述所有输入参数的不确定度得到燃料中心温度和包壳表面温度的不确定度,如图3所示。
图3表明,对于TMI-1压水堆燃料棒在0~60 GW·d/tU的燃耗过程中,燃料中心温度的不确定度在同一功率水平下随燃耗的加深逐渐增大;包壳表面温度的不确定度随燃耗的加深变化不大,约为±5 ℃。

图3 最大燃料中心温度和包壳表面温度及其不确定度(3σ)
3.3 组件燃耗计算
采用西安交通大学NECP实验室自主开发的压水堆少群常数计算软件NECP-Bamboo_Lattice[11-12],对燃耗过程进行模拟仿真计算。组件功率密度设置为33.75 W/gU,初始燃料组件为全新,燃耗深度为60 GW·d/tU。
采用西安交通大学NECP实验室自主开发的不确定度量化分析程序平台NECP-UNICORN进行不确定度分析。采用统计学抽样方法,分别对核数据以及几何参数的不确定度进行抽样。对于核数据的不确定度,协方差来自于ENDF/B-Ⅶ.1评价核数据库[13],并利用核数据处理程序NJOY[14]处理成WIMS-69群格式,具体核素列于表3。几何参数及其不确定度来自于UAM-LWRs Phase Ⅱ的基准题手册,如表4所列。

表3 燃料组件燃耗不确定度量化所考虑的核素

表4 几何参数的不确定度
由于不同类型的核反应截面之间具有相关性,因此采用COST方法对核数据进行抽样,样本容量等于协方差矩阵的秩,为167。几何参数之间没有相关性,因此采用拉丁超立方体抽样(LHS),样本容量为167。根据以前的研究结果,该样本容量能满足抽样的精度要求。
组件特征值kinf及其不确定度(1σ)随燃耗的变化如图4所示。从图4可看出,寿期初的kinf不确定度最大,为850 pcm;随着燃耗的加深,特征值的不确定度逐渐减小,寿期末的kinf不确定度为475 pcm。
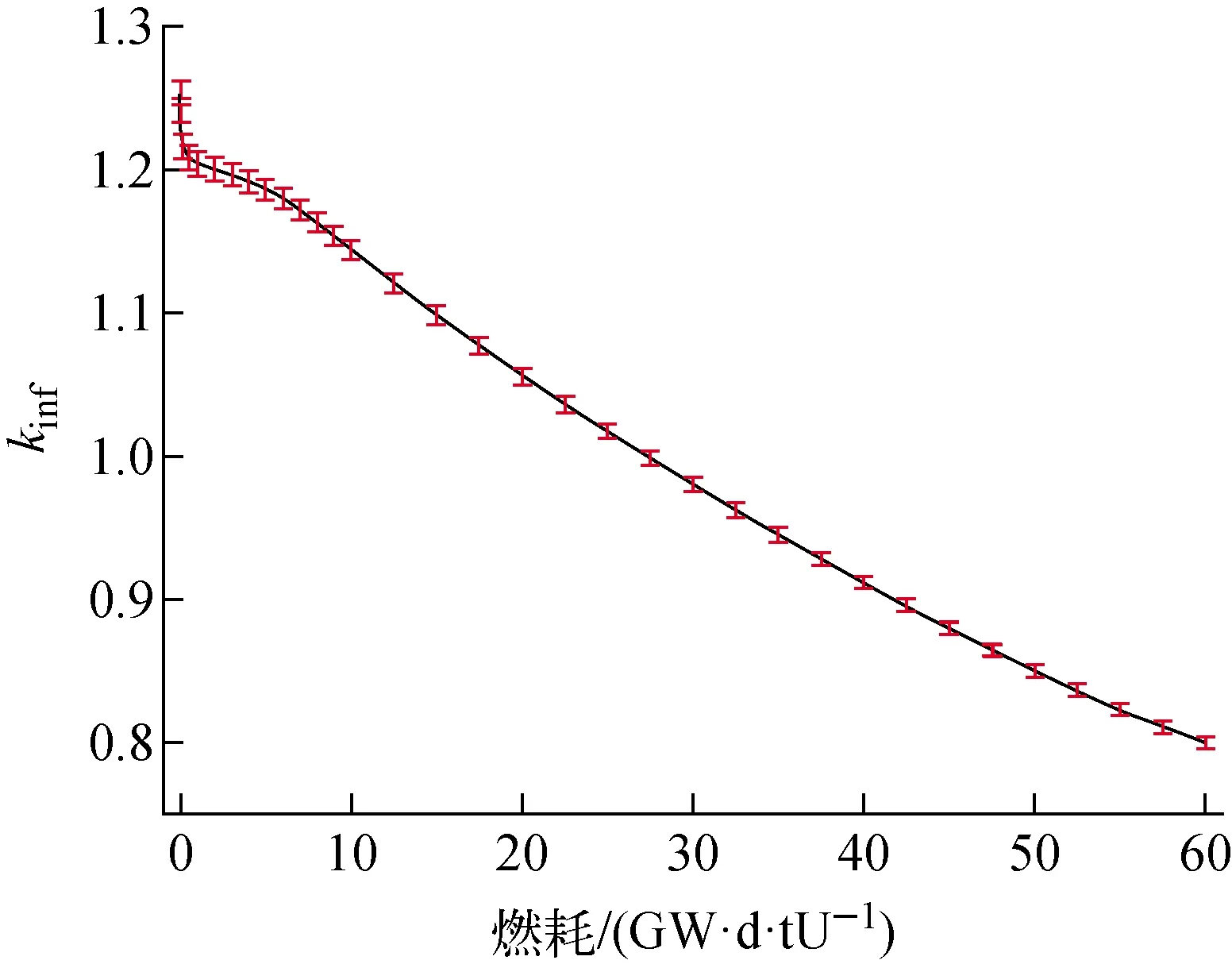
图4 kinf及其不确定度(1σ)随燃耗的变化
寿期初和寿期末的组件棒功率分布及其相对不确定度(1σ)如图5所示。由图5可见,功率相对不确定度最大值出现在含Gd燃料棒处,寿期初为0.60%,寿期末为0.28%。随着燃耗的加深,组件功率分布逐渐展平,所以功率相对不确定度也逐渐减小。
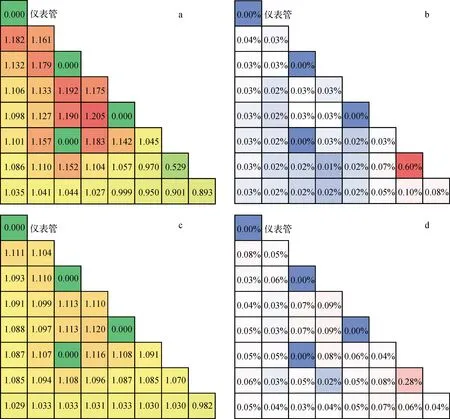
a——寿期初组件功率分布;b——寿期初功率相对不确定度;c——寿期末组件功率分布;d——寿期末功率相对不确定度
两群常数的相对不确定度列于表5。从表5可看出,两群常数D1、D2和散射截面Σa1、Σa2的不确定度随燃耗的变化不大,而宏观裂变产额νΣf,1和νΣf,2随燃耗的加深,相对不确定度显著增大。235U、238U、239Pu和241Pu 4种重核素的核子密度的相对不确定度随燃耗的变化如图6所示。由图6可看出,随着燃耗的加深,235U核子密度的相对不确定度逐渐升高,最大为3.23%;238U核子密度的相对不确定度基本保持不变,约为0.36%;239Pu和241Pu的核子密度开始逐渐增多,相对不确定度也逐渐增大,寿期末分别为2.78%和2.54%。

图6 核子密度及其相对不确定度

表5 两群常数的相对不确定度
3.4 热工水力分析
为分析TMI-1燃料组件输入参数的不确定度在热工水力计算中的传递过程,采用热工水力子通道程序CTF[15]进行建模,分别考虑稳态和瞬态过程的不确定度量化。采用拉丁超立方体抽样,根据对不同样本数量统计涨落的研究[10],样本容量选为200,分别对边界条件、模型系数和几何参数进行抽样。在热工水力分析的不确定度量化领域,通常会根据现象识别与排序表(PIRT表)来识别不确定度来源,并结合敏感性分析和实验数据来确定不确定度的范围和分布。本文所研究参数及其不确定度来自于UAM-LWRs Phase Ⅱ的基准题手册,需要考虑的参数以及不确定度范围如表6所列。
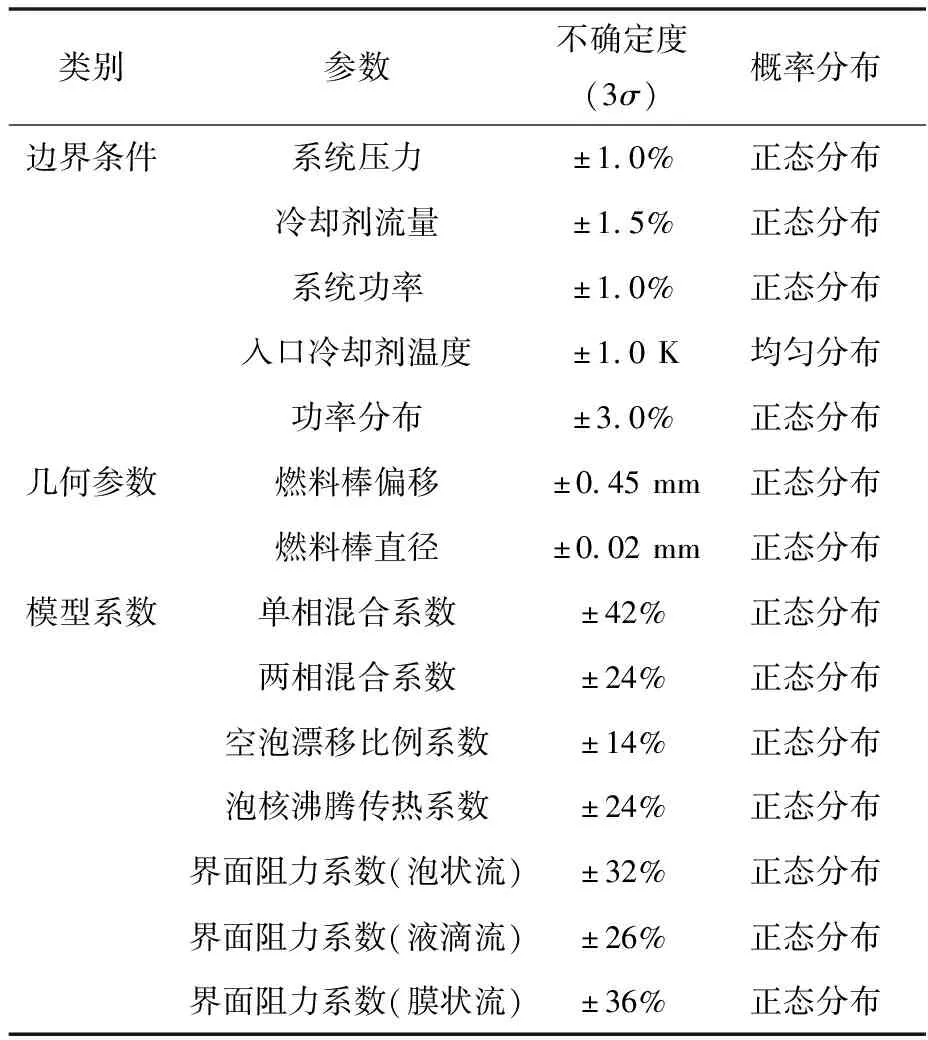
表6 热工水力分析过程输入参数的不确定度
1)稳态分析
稳态分析的组件功率为3.915 MW,系统压力为15.2 MPa,入口冷却剂温度为291.85 ℃,冷却剂流量为20.5 kg/s。稳态热工水力分析结果的不确定度如表7所列,最大冷却剂温度为(325.20±1.05)℃,最大包壳温度为(336.80±1.29)℃,冷却剂压降为(31.50±0.12)kPa。其中一个子通道的冷却剂温度和包壳温度随轴向高度的变化及其不确定度如图7、8所示。
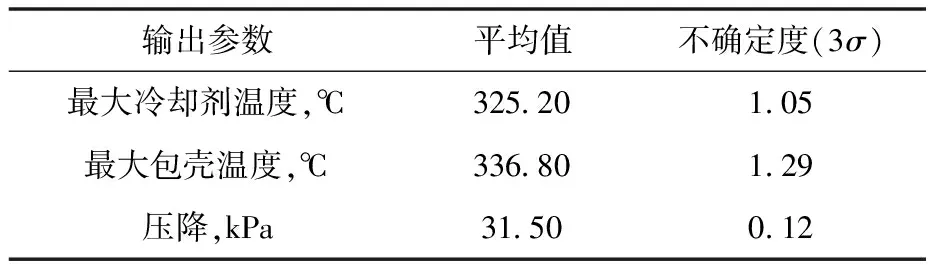
表7 稳态热工水力分析结果的不确定度

图7 子通道冷却剂温度及其不确定度

图8 子通道包壳温度及其不确定度
2)瞬态分析
瞬态起始状态与稳态相同,瞬态过程中各边界条件的变化如图9所示。功率、压力和入口冷却剂温度基本保持不变,冷却剂流量在0~2.6 s内逐渐降低,随后又逐渐升高。瞬态过程在0、2.6、5.0 s时,冷却剂出口温度如图10所示。最大出口冷却剂温度位于组件中心处,且在整个瞬态过程中不断升高。
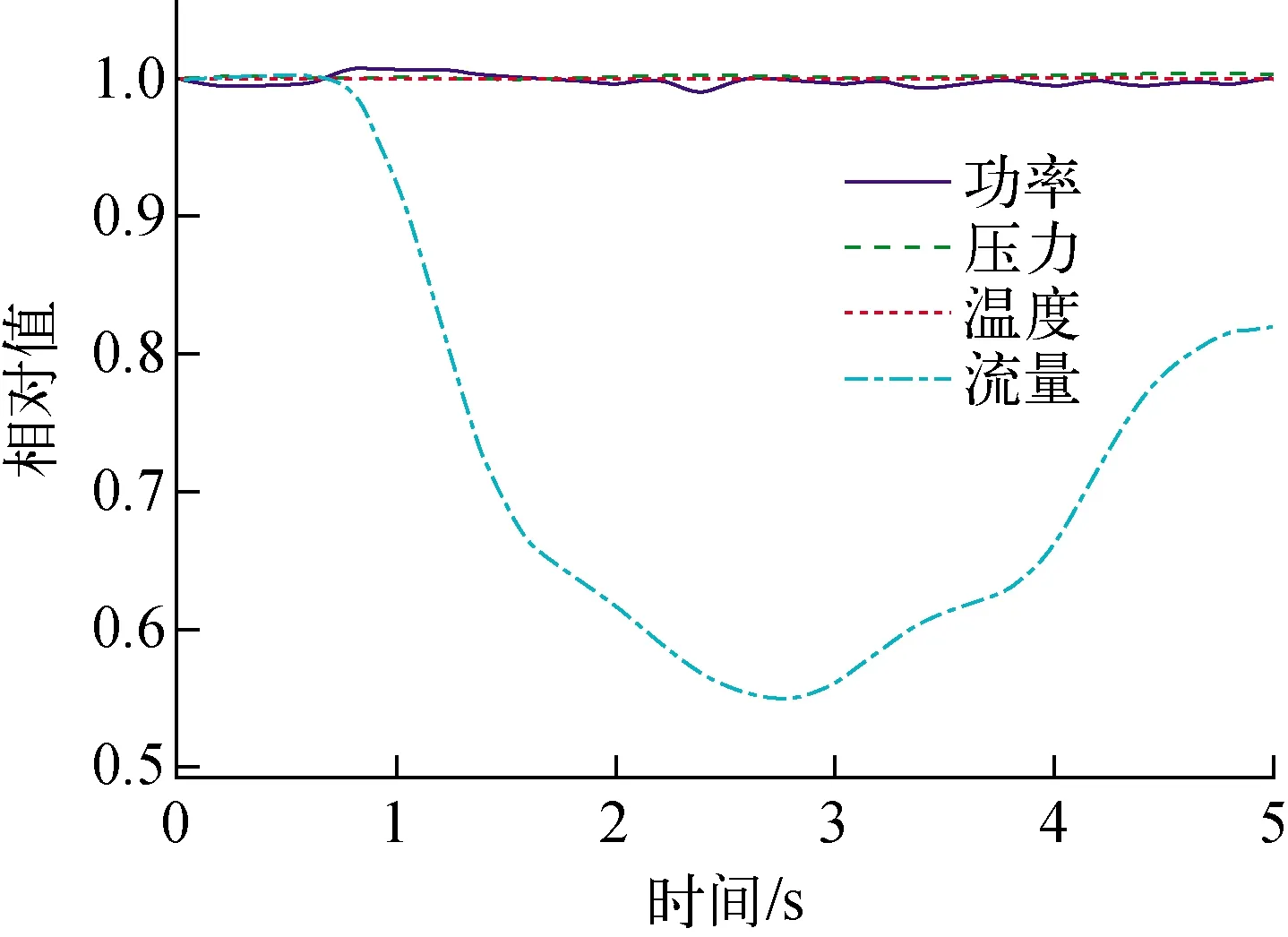
图9 TMI-1燃料组件瞬态过程曲线

图10 瞬态过程冷却剂出口温度
瞬态过程最大冷却剂温度、最大包壳温度及其不确定度如图11所示。由图11可见,在初始状态,包壳最大温度为(338.00±1.27)℃,冷却剂最大温度为(326.00±1.06)℃;5.0 s时,包壳最大温度为(345.00±0.62)℃,冷却剂最大温度为(335.00±1.14)℃。
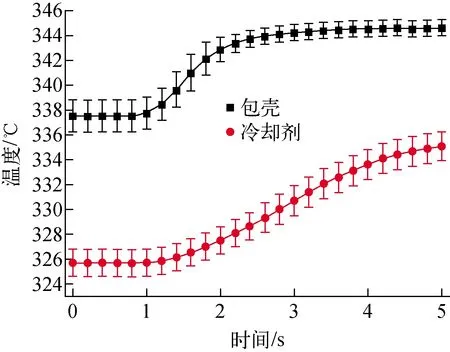
图11 瞬态过程冷却剂和包壳最大温度及其不确定度(3σ)
4 结论
本文基于不确定度分析程序NECP-UNICORN,对不确定度量化基准题UAM-LWRs Phase Ⅱ中描述的TMI-1燃料组件进行燃料性能分析、燃耗计算和热工水力分析的不确定度量化研究。燃料性能分析需要考虑边界条件、几何参数和材料特性的不确定度,燃耗计算需要考虑核数据、几何参数的不确定度,热工水力分析需要考虑边界条件、几何参数以及模型系数的不确定度。
对于TMI-1燃料棒,燃料中心温度的不确定度在同一功率水平下随燃耗的加深逐渐增大;包壳表面温度的不确定度随燃耗的加深变化不大,约为±5 ℃。对于TMI-1燃料组件,在寿期初kinf的不确定度最大,为850 pcm;随着燃耗的加深,特征值的不确定度逐渐减小,寿期末kinf的不确定度为475 pcm。对于TMI-1燃料组件,稳态最大包壳温度为(336.80±1.29)℃,最大冷却剂温度为(325.20±1.05)℃。在瞬态过程结束时,包壳最大温度为(345.00±0.62)℃,冷却剂最大温度为(335.00±1.14)℃。
