高保真中子输运计算的多级加速理论及应用

郝 琛，朱雁凌，康 乐，李佩军，周晓宇

(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001)

数字化反应堆是反应堆设计、安全运行、退役等过程的研究平台，已成为当前核工业领域的研究热点。高保真中子输运计算提供精细的时空中子分布，是数字化反应堆核心功能之一。然而，计算时间过长已成为制约反应堆高保真中子输运计算的瓶颈。研究适用于数字化反应堆高保真中子输运计算的加速方法，并在高性能计算平台成功实施，是破解该难题的关键。

目前，精细化中子输运计算的加速方法日益成熟，主要可将其分为两类：针对中子输运源迭代过程的迭代加速方法和针对瞬态中子输运计算的时间步加速方法。迭代加速法主要包括粗网再平衡方法、粗网有限差分方法(CMFD)等，其中CMFD具有加速效果好、易于实施、适用范围广等优点，在高保真中子输运计算程序中被广泛使用，如DeCART[1]、MPACT[2]、NECP-X[3]、HNET[4]等。传统的CMFD一般只在空间上实施一级加速，近年来为降低CMFD引入的计算负担，逐渐发展形成了两级加速及三级加速理论，如Joo和Yee等[5-6]在空间和能量上开展两级CMFD加速；Seungsu等[7]采用两级pCMFD加速输运计算；Liu等[8]将三级CMFD应用在NECP-X上，实现了输运计算的加速。近年来，随着高性能计算集群的快速发展以及计算精度标准的提高，瞬态中子输运方程的求解方法已成为一个研究热点，相应的也出现了多种时间步加速方法，其中较为典型的是预估校正准静态方法(PCQM)[9]。PCQM具有极大节省时间的优势，但它在处理中子通量密度变化较为迅速的复杂问题时存在较大误差。NECP-X通过改进传统PCQM克服了这个缺陷[10]，但并没有在计算效率方面改善。为充分利用预估校正准静态的优势，MPACT采用瞬态多级方法(TML)[11]，通过两次运用预估校正准静态方法，在保证计算精度的同时，提升整体计算效率。虽然TML的效果十分突出，但这样的加速并不充分，同时还面临着多群CMFD计算时间占比过大的问题。

综上所述，单独时间步上的加速，以预估校正准静态方法等为代表的方法，提供了很好的思路；而在空间、能群等尺度上的加速，粗网有限差分方法提供了很好的思路。但在前期的研究中，这两种加速思路及方法是相对独立应用的。本文将时间、空间、能量、角度方面的加速方法整合在统一的方法框架下，形成一套完整的多级加速理论，并将这套理论应用到HNET中，旨为实现更高效、准确的高保真中子输运计算。

1 多级加速理论

1.1 时间步加速思路

瞬态中子输运计算中，通常将最耗时的高保真中子输运计算放在尽可能大的时间步上，从而减少中子输运计算的计算量，实现时间步加速。然而，针对时间导数项，以差分代替微分时，时间步长增大时差分误差也会增大，进而严重影响瞬态输运计算的精度。预估校正准静态方法的出现为解决该问题提供了很好的思路。如式(1)所示，预估校正准静态方法将中子通量密度因式分解为仅与时间相关的幅函数Φ(t)和同时与时间、空间、能量、角度相关的形状函数Ψ(r,E,Ω,t)的乘积，进而分别求解幅函数和形状函数。

φ(r,E,Ω,t)=Φ(t)Ψ(r,E,Ω,t)

(1)

于是，形状函数可由式(2)求得：

Ψ(r,E,Ω,t)=φ(r,E,Ω,t)/Φ(t)

(2)

分析式(2)可知，形状函数虽然还与时间t相关，但已经去除了与时间变化较快的幅值项。因此，形状函数随时间的变化缓慢，远慢于幅函数，而实际堆芯中正是如此。因式分解的本质就是希望去除与时间变化较快的项，使得差分代替微分的误差尽量小，这样才可以保证在大时间步上，时间微分项用差分代替后的精度足够高。

式(2)计算时假设幅函数已知，但实际求解中是未知的，还需建立等价的低阶系统来求解。幅函数的求解依赖于形状函数，因此需要高阶系统为低阶系统提供均匀化参数及预估的中子通量分布信息，实现在小时间步长求解低阶、等价系统，以获取小时间步长的幅函数，进而校正大时间步长的中子通量密度，保证其计算精度。预估校正准静态方法将高保真中子输运计算得到的大时间步长t的形状函数ΨP(r,E,Ω,t)和小时间步长t′的精确点堆动力学计算得到的幅函数pC(t′)代入式(1)，得到校正后小时间步长t′的中子通量密度为：

φC(r,E,Ω,t′)=pC(t′)ΨP(r,E,Ω,t)

(3)

式中，上标C表示校正后的变量，P表示预估的变量。

在预估校正准静态方法中，点堆动力学计算幅函数后，基于式(2)所得的形状函数仍具有全局空间分布的差别，导致在使用差分代替微分时，时间步不能太长，否则高保真中子输运计算精度将无法保证，严重影响加速效果。事实上，形状函数和幅函数实际上并不具有天然的唯一性，是可以调整二者作用范围的，如式(4)所示：

φH(r,E,Ω,t)=ΦL(R,E′,Ω′,t)ΨH(r,E,Ω,t)

r∈R，E∈E′，Ω∈Ω′

(4)

式中：φH(r,E,Ω,t)为较高分辨率的中子通量密度；ΦL(R,E′,Ω′,t)为较低分辨率的幅函数；ΨH(r,E,Ω,t)为较高分辨率的形状函数。通过调整因式分解的作用范围，时间步的多级加速可以作用于不同的分辨率系统，如空间方面有Sub-pin级别的细网、Pin级别的粗网、全堆芯级别等。因而为表征中子通量密度分布随时间、空间、能量、角度的变化趋势，可以通过较高分辨率的幅函数来实现，以保证高保真中子输运计算解与幅函数的比更接近于1，这样才能保证在更大的时间步上，高保真中子输运的时间微分项用差分代替后精度足够高，实现了精度和计算速度的综合提高。

因此，针对传统PCQM的问题，可引入多级加速的思想解决，即在高保真中子输运计算与点堆动力学计算之间引入新的CMFD计算，CMFD全局求解可以获得不同时间步长内的全局中子通量分布信息，以逐级修正高阶中子通量，保证在相同时间步长下，提高计算精度；在扩大时间步长时，保持与小时间步长计算一致的精度，真正实现了高保真中子输运的加速计算。

1.2 迭代加速思路

在精细化瞬态中子输运计算的迭代过程中，精细的离散网格导致了较高的计算代价，难以快速计算得到精细的中子通量密度分布。针对此问题，CMFD提供了很好的迭代加速思路[4]。在迭代求解过程中，中子通量密度的收敛速度取决于其初值与最终收敛值间的残差，可通过空间、能量、角度方面的低分辨率系统为高分辨率的精细化中子输运计算提供良好初值，使其更接近于收敛值，从而减少迭代次数，实现迭代加速。但用于加速的低阶系统求解会引入额外的计算负担，尤其瞬态模拟，CMFD求解时间可与MOC中子输运求解时间相当。因此，通过低分辨率系统实现高效迭代加速需要两个前提：1)低分辨率系统必须与高分辨率的中子输运系统严格等价，确保加速的可行性；2)低分辨率系统自身的计算代价必须足够低，确保其增加的额外计算负担不会过大。

为满足这两个前提，以进一步提高计算速度，可引入多级加速的思想：1)能群多级加速，如建立等价单群CMFD，以进一步加速多群CMFD；2)空间多级加速，如建立1/4栅元CMFD或平源区CMFD系统，并以等价空间大网格CMFD加速；3)混合多级加速，如能群及空间的混合多级加速等。而针对CMFD源迭代收敛慢的问题，可采用Wielandt Shift技术加速。该迭代加速思路可应用于多种形式的CMFD，如基于广义等价理论的CMFD(gCMFD)[12]、最佳扩散CMFD[13]、基于偏流的CMFD[14]、以线性近似解代替均匀解的lpCMFD[15]等。

1.3 多级加速框架的建立

基于时间步加速思路和迭代加速思路可建立高保真中子输运计算的多级加速框架，如图1所示。

图1 多级加速框架示意图

关于时间步加速，在时间变量t的离散过程中，采取逐级划分时间步长的策略[16]，即耗时最长的三维高保真中子输运计算时使用最大时间步长Δt，在Δt内再次划分次级时间步长Δt1，以用于三维多群CMFD计算。以此类推，在Δt1时间步长内再次划分小时间步长Δt2用于三维单群CMFD计算，在Δt2内划分最精细的时间步长Δt3以用于精确点堆动力学(EPK)计算。该策略将耗时最长的高保真中子输运计算在最大时间步上开展，以大幅减少高保真中子输运计算的计算量，实现加速。进而，基于预估校正准静态方法，保证高保真中子输运计算在大时间步下具备所要求的计算精度。在不同时间步长下，捕捉不同空间、能群分辨率的中子通量密度特征，即通过高保真中子输运计算，获得细网、多群的中子通量密度特征；通过等价的多群CMFD计算，获得粗网、多群的中子通量密度特征；通过等价的单群CMFD计算，获得粗网、单群的中子通量密度特征；通过等价的精确点堆动力学计算，获得全堆芯、全空间的中子通量密度特征。再次基于预估校正的思想，逐级代回、逐级校正，保证细网、多群中子通量密度的计算精度的前提下，充分利用小时间步等价系统的快速求解减少了高保真中子输运计算的计算量，采用多级加速实现了有效的时间步加速。

而在不同时间步内的中子输运计算迭代过程中，又引入了迭代加速策略[17]。即针对大时间步下的高保真中子输运计算，通过等价的平源区多群CMFD或1/4栅元多群CMFD或栅元多群CMFD加速高保真中子输运计算的源迭代过程；通过等价的单群CMFD加速多群CMFD的源迭代过程；通过Wieland Shift技术加速单群CMFD源迭代过程。最终，实现不同时间步下的高保真中子输运迭代求解或多群CMFD迭代求解。在迭代加速过程中，本文采用gCMFD方法保证不同分辨率系统的完全等价性。gCMFD方法通过引入节块不连续因子和扩散系数修正因子，建立了与高保真中子输运计算的严格等价的线性系统，同时也保证了线性系统的数值计算稳定性，实现了高效加速。关于gCMFD方法的理论推导可参考文献[12]。

在该多级加速框架中，针对时间步的多级加速的核心是多级预估校正准静态方法，针对迭代加速的核心是多级gCMFD方法。其中包括了时间步尺度的四级加速、空间尺度的三级加速、能群尺度的两级加速、空间角度的一级加速。最终，基于多级加速框架，实现了在不同时间、空间、能量、角度分辨率下的多级加速，最终实现对高保真中子输运计算的有效加速。

1.4 时间步加速过程中精度和计算速度综合提高的策略

在时间步加速过程中，需通过在更小时间步上求解等价低阶系统获取幅函数，进而校正大时间步长的中子通量密度，以保证计算精度。下面以高保真中子输运计算与多群CMFD计算的组合为例，来进一步阐述精度和计算速度综合提高策略的一些细节问题。

首先，基于多级加速框架，在大时间步长Δt上开展高保真中子输运计算，并预估中子通量密度φ(r,E,Ω,t)的形状函数Ψ(r,E,Ω,t)。针对多群CMFD的粗网i及其内部某一细网位置r，应用式(1)可得：

φ(r,E,Ω,t)=Φi(E,t)Ψ(r,E,Ω,t)r∈i

(5)

式中：φ(r,E,Ω,t)为细网r内高保真中子输运的中子通量密度；Ψ(r,E,Ω,t)为细网r内中子通量密度的空间-角度形状函数；Φi(E,t)为粗网i内多群CMFD计算得到的幅函数。

为保证因式分解的唯一性，需对细网内形状函数做出限制，强制细网形状函数在每个粗网内的空间-角度积分保持定值，即：

(6)

求解多群CMFD可得到粗网均匀化的中子标通量密度。若要通过多群CMFD计算获得幅函数Φi(E,t)，需进一步明确粗网均匀化中子标通量密度与幅函数的关系。于是，在粗网i内将式(5)对空间和角度进行积分，并用式(6)代入可得：

(7)

(8)

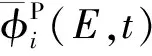
r∈i

(9)

r∈i

(10)

如此，实现了在更大时间步上求解高保真中子输运计算，从而实现加速。并且通过较小时间步上的多群CMFD求解获得幅函数，以校正高保真中子输运计算解，保证计算精度。

2 数值结果与分析

2.1 多级加速理论的实施策略

HNET程序采用堆芯一维轴向先进节块展开法(NEM)或离散纵标法(SN)耦合堆芯二维径向特征线法的2D/1D方法开展全堆芯三维精细化中子输运计算，并应用多级加速理论进行加速。图2为基于多级加速理论的瞬态中子输运计算流程图，由4种不同分辨率的求解器和3级耦合算法构成，在不同分辨率上捕捉中子通量密度随时间、空间、能量和角度的变化。其中，采用两级gCMFD方法加速预估瞬态输运计算的迭代过程，其流程如图3所示。

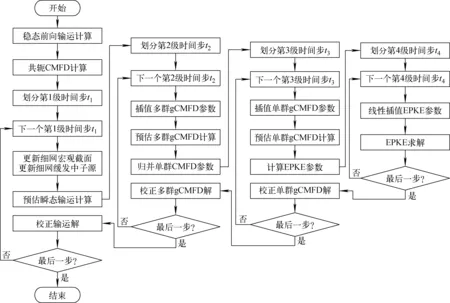
图2 基于多级加速理论的瞬态中子输运计算流程图

图3 两级gCMFD迭代加速的流程

由图2、3可知，各加速环节的收敛准则会影响最终的迭代次数以及计算耗时。各求解器收敛准则列于表1，HNET采用中子通量密度的残差作为瞬态中子输运计算的收敛判据。瞬态高保真中子输运计算的收敛准则为MOC细网裂变源的相对误差的无穷范数，小于10-4，而多群和单群gCMFD的收敛准则是粗网均匀化裂变源的相对误差的无穷范数，分别小于10-8和10-10。此外，对不同加速过程的求解器预先设置迭代次数的上限。当达到收敛标准或超过最大迭代次数时，结束对求解器的调用。

表1 各求解器收敛准则

HNET程序相关参数设置如下：对于三维非均匀单组件弹棒问题，射线间距选择0.05 cm，角度选择每卦限16个方位角和2个极角配合Tabuchi-Yamamoto极角求积组[18]；对于三维C5G7-TD基准题，射线间距选择0.03 cm，角度选择每卦限16个方位角和3个极角配合Tabuchi-Yamamoto极角求积组。所有算例均采用2.60 GHz Intel Xeon E5-2690 v4 CPU计算，实施轴向区域分解并行方案。

2.2 三维非均匀单组件弹棒问题

为验证多级加速理论的加速效果，采用不同方案计算三维非均匀单组件弹棒问题。该问题的径向几何结构如图4所示，轴向上共28个轴向层，其中活性区被分为24个5 cm的轴向层，顶底反射层均被划分成2个10 cm轴向层，径向为反射边界，轴向则是真空边界。输运计算采用51群结构的宏观截面，动力学参数来自C5G7-TD基准题[19]。

图4 单组件径向几何布置

该问题为阶跃弹棒事件，初始时刻位于组件正中心的单根控制棒在活性区中的插入深度为55 cm，而后立刻阶跃弹出，引入正反应性，整个瞬态过程持续0.12 s。表2列出不同算例的计算方案，表中MG、1G和EPK分别代表多群gCMFD、单群gCMFD步及精确点堆动力学。

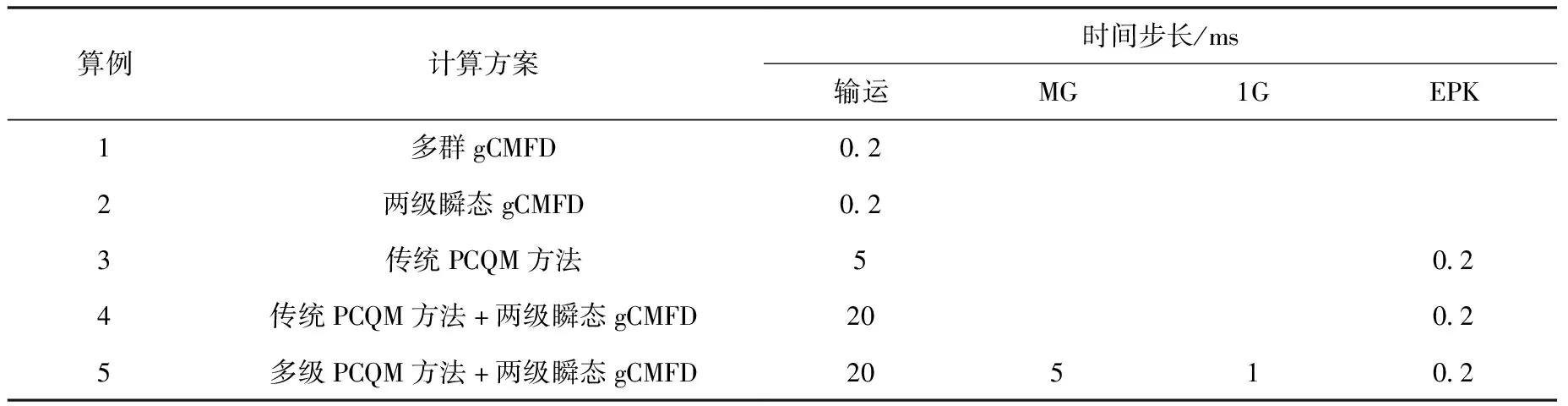
表2 不同算例的计算方案

算例1只采用多群gCMFD方法且使用了最精细的输运时间步长，将其计算结果作为基准解。图5为三维单组件阶跃弹棒问题堆芯相对功率和反应性的计算结果，图6为其他算例的堆芯功率与算例1基准解的相对误差。由图5、6可知，对于三维单组件阶跃弹棒问题，除算例4外，其他算例的计算结果均能与算例1很好地吻合。

图5 单组件问题数值结果

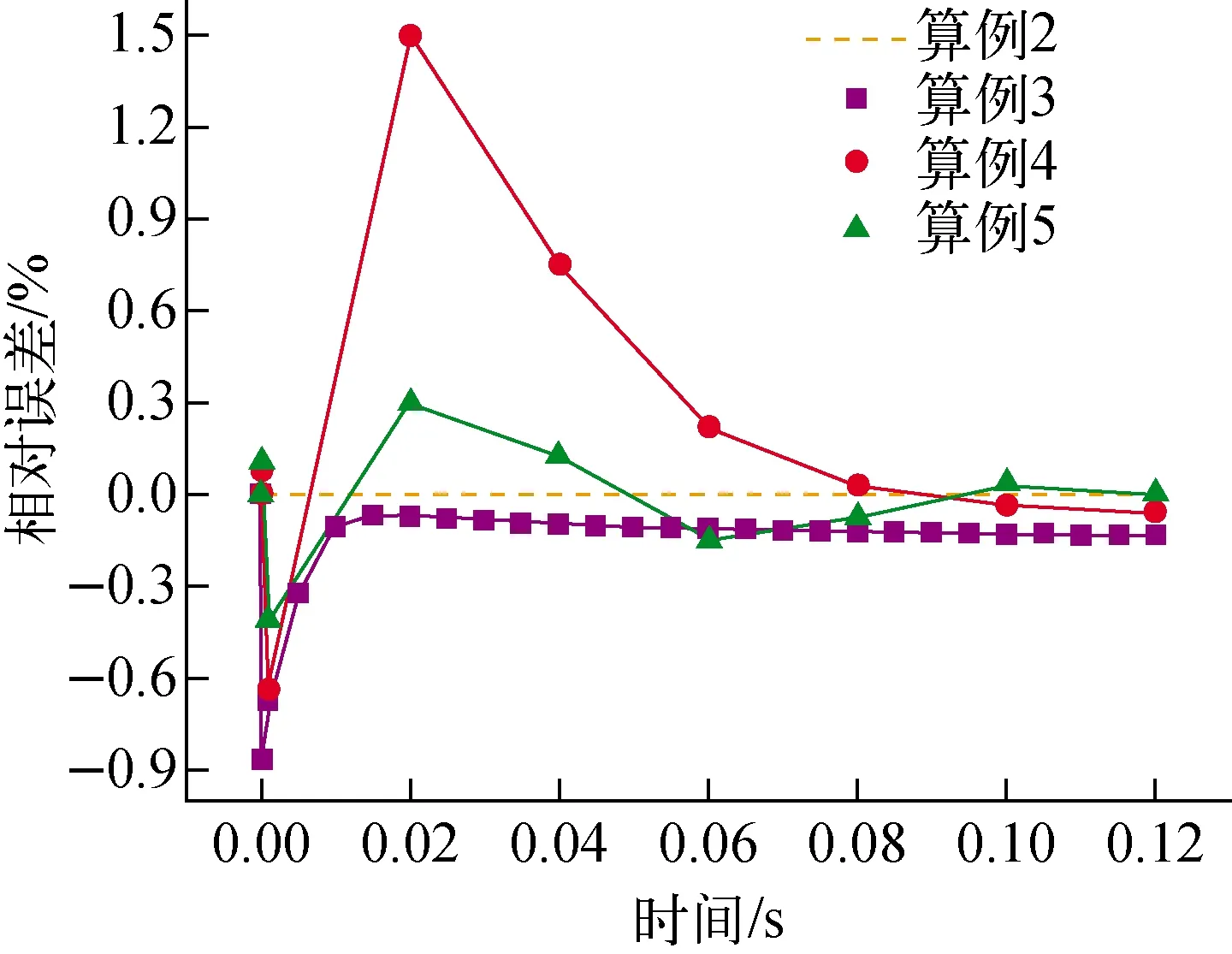
图6 单组件问题堆芯功率的相对误差

表3统计了各算例的求解器耗时、迭代次数以及均方根误差。算例2使用两级瞬态gCMFD方法开展迭代加速，在MOC方面的耗时和迭代次数与算例1几乎相同。但与算例1相比，两级瞬态gCMFD方法通过单群gCMFD加速可将多群gCMFD的迭代次数降低约91%，进而将求解器总耗时减少约47%，有效地减轻了多群gCMFD的计算负担。对比算例1和算例3可知，传统的PCQM方法在保证计算精度的前提下能适当地扩大时间步长，减少输运计算的次数，从而降低求解器总耗时。但由算例4可知，对于阶跃弹棒问题，传统PCQM方法无法准确地修正大时间步长下的中子通量密度分布，并且两级瞬态CMFD方法的迭代加速无法改善时间导数项的误差。算例5采用多级PCQM方法，可有效捕捉不同分辨率中子通量密度形状和幅值随时间的变化，能够在大时间步长下提供较为准确的修正因子，从而提高计算精度。同时，算例5综合了时间步加速和迭代加速的优点，不仅能有效地减少瞬态中子输运的计算次数，还降低多群gCMFD的计算耗时，将求解器总耗时降至算例1的3.88%。可见，整合时间步加速思路和迭代加速思路对实现更高效、准确的高保真中子输运计算是非常有益的。

表3 堆芯功率均方根误差与求解器耗时

2.3 三维C5G7-TD基准题

为考察多级加速理论在堆芯输运计算方面的适用性，采用C5G7-TD系列基准题做进一步验证。C5G7-TD系列基准题包括二维问题和三维问题，其中三维问题包含TD4和TD5两个系列，具体几何结构、截面信息、动力学参数以及瞬态事件可由文献[19]获得。TD4系列包含5个三维堆芯中不同组件的控制棒线性移动事件：在初始时刻，所有控制棒均处于顶部反射层内，随后在0～8 s过程中，不同组件的控制棒以不同的速度匀速地插入反应堆而后提出。TD5系列包含4个三维堆芯中不同组件的慢化剂密度变化事件：在整个瞬态过程中，所有控制棒均完全撤出三维堆芯，在0～4 s过程中，不同组件的慢化剂密度以不同的速度匀速地降低而后上升。TD4问题各组控制棒均在8 s后回到初始时刻的位置，TD5问题各组件的慢化剂密度在4 s后回到初始值。

TD4和TD5系列问题均选取25 ms和125 ms两种输运时间步长开展计算，从而对比验证HNET的加速效果，其中25 ms输运时间步长的数据结果来自文献[20]。图7展现了不同输运时间步长下，TD4和TD5系列问题堆芯相对功率的变化。在TD4-1、TD4-2和TD4-3中不同控制棒组的移动方向相同，随着控制棒的匀速插入，在初始时刻后堆芯相对功率逐渐降低，而后在匀速提棒过程中，堆芯相对功率逐渐回升。在TD4-4和TD4-5中存在两组控制棒移动方向相反的情况，导致这两个算例堆芯相对功率的变化更加复杂。对于TD5系列问题，堆芯相对功率的变化趋势与慢化剂密度的变化趋势一致。从图7可知，TD4和TD5问题的堆芯相对功率分别在8 s和4 s后逐渐趋于稳定，但由于缓发中子先驱核浓度随着瞬态过程的进行有所降低，堆芯相对功率最终无法回到初始值。

图7 堆芯相对功率的变化

为评估数值计算结果的准确性，将MPACT采用TML方法得到的数值结果[21]作为参考值。图8、9分别为TD4、TD5系列问题堆芯相对功率与MPACT的相对误差。从图8、9可知，在控制棒移动和慢化剂密度变化的过程中，相对误差的波动比较大。不过，总体上各算例堆芯功率的相对误差都比较小，25 ms和125 ms输运时间步长的最大相对误差分别为0.54%、0.74%。这表明HNET数值结果能与MPACT参考解吻合得很好，细微的偏差主要由空间离散策略和尖端效应的处理方式引起[21]。此外，结合图7～9可知，通过多级加速理论，使用较大时间步长的计算精度能与使用较小时间步长的计算精度处于相同的水平。整体计算结果表明，应用多级加速理论的HNET程序已经具备高精度的三维瞬态中子输运计算能力。

图8 TD4问题的堆芯功率相对误差

图9 TD5问题的堆芯功率相对误差

表4将三维C5G7-TD问题的计算耗时与MPACT对比。HNET程序采用32个计算核进行瞬态计算，计算核数与MPACT一致。同时，HNET与MPACT均采用细网裂变源相对误差的无穷范数作为收敛判据，收敛准则均为10-4。

从表4可知，相比于MPACT程序，HNET程序在计算效率上明显更具优势。首先，在输运时间步长同为25 ms的情况下，HNET程序通过迭代加速的方法能把多群gCMFD的计算负担降低，因而计算总耗时比MPACT少。其次，HNET程序通过时间步加速方法，可在保持计算精度的前提下扩大输运时间步长，减少瞬态中子输运的计算量，从而进一步降低计算总耗时。总的来说，HNET程序通过多级加速理论，在保证计算精度的同时，实现了对高保真中子输运计算的有效加速。

表4 C5G7-TD三维问题的总耗时对比

3 结论

本文基于时间步加速方法和迭代加速方法，研究适用于高保真中子输运计算的多级加速理论，为解决输运计算时间消耗过长的问题提供理论指导，主要结论如下。

1)与传统PCQM方法比，多级PCQM方法能在大时间步长下提供较为准确的修正因子，实现计算精度和计算速度的综合提高；针对不同时间步下的中子输运计算，可通过等价的低分辨率系统减少高分辨率系统计算的迭代次数以加速计算，最终实现全堆芯高保真三维中子输运计算的快速求解。

2)对于三维C5G7的TD4和TD5系列问题，HNET程序的计算结果均能与MPACT程序的结果很好地吻合，具有相当的计算精度。而且HNET程序在保证计算精度的同时，具有优于MPACT的计算效率。这表明HNET程序已具备高保真三维全堆芯瞬态中子输运计算能力，能为数字化反应堆研究的开展提供可靠的计算平台。