数值反应堆堆芯通道级三维热工水力程序CorTAF开发及初步验证
2022-03-02王明军田文喜秋穗正苏光辉
刘 凯,王明军,田文喜,秋穗正,苏光辉
(西安交通大学 核科学与技术学院,动力工程多相流国家重点实验室,陕西省先进核能技术重点实验室,陕西 西安 710049)
反应堆堆芯作为包容放射性裂变产物的场所,在核动力系统运行周期内保持高度可靠性和完整性对于提升核动力系统安全性具有重要意义。传统的核反应堆堆芯热工水力分析方法大多采用一维或集总参数分析方法[1-3],无法满足未来先进核动力系统的设计研发及安全分析需求。近年来,随着计算机技术的发展和数值反应堆的提出,计算流体力学(CFD)目前已广泛应用于核反应堆安全分析中[4-7],但对堆芯的复杂棒束结构进行精细建模的计算资源消耗巨大,不利于开展全堆芯模拟。子通道方法广泛应用于棒束组件和堆芯计算中,是目前国际上进行堆芯热工水力模拟的主要技术手段[8-11],该方法认为棒束间冷却剂为平行一维流动,将堆芯划分为具有多个节点的不同子通道,计算其轴向流动,并考虑横向流动在不同通道引起的质量、动量、能量交换,但程序模型中仅建立轴向动量守恒方程,而不区分不同方向的横向流动,严格意义上不具有三维流动物理意义,且如COBRA、FLICA等程序开发时间较早、架构老旧,不便于开展多物理场耦合和大规模并行计算。
OpenFOAM平台采用面对对象编程的C++语言,具有编程环境开放、并行能力强大等诸多优势,相比于开放程度较弱的商业CFD软件,便于进行数据接口创建、模型修改植入及求解器编写,更好地满足用户自主开发的需求,已在航空航天、海洋船舶、化工过程等领域得到广泛应用。依托该平台开展反应堆堆芯数值模拟研究、形成自主可控的全堆芯热工水力特性分析平台将是反应堆安全研究的一个重要方向。
本文依托开源CFD平台OpenFOAM,针对压水堆堆芯棒束结构特点,建立冷却剂流动换热模型、燃料棒导热模型和耦合换热模型,开发一套基于有限体积法的压水堆全堆芯热工水力特性分析程序CorTAF,选取GE3×3、Weiss和PNL2×6燃料组件流动换热实验开展模型验证。
1 模型建立
1.1 冷却剂流动换热模型
本文基于有限体积法,建立考虑冷却剂通道几何结构的质量、动量、能量守恒方程。对压水堆堆芯内冷却剂通道建立控制体ABCD-A′B′C′D′,其顶点位于通道四周燃料棒的轴心位置,如图1所示。

图1 冷却剂通道控制体示意图
控制体几何中心为P点,控制体体积为VP,边界面为f,平行主流方向的边界面面积为Sf,t,垂直主流方向的边界面面积为Sf,a,控制体沿主流方向长度为L,燃料棒直径为d。由守恒关系,通道内冷却剂各物理量φ在控制体内满足对流扩散方程[12],对其积分后离散得到控制方程:
(1)
式中:ρ为冷却剂密度;Δt为时间步长;u为冷却剂速度;Sf为面通量;Sφ为物理量源项;Γφ为物理量广义扩散系数;上角标n和n-1分别代表当前和上一时间步;下角标f代表界面值。
考虑真实冷却剂通道中控制体的部分空间被燃料棒占据,根据几何参数有:
(2)
S′f,t=Sf,t-dL
(3)
(4)
其中:V′P为冷却剂通道体积;S′f,t和S′f,a为平行和垂直主流方向的冷却剂通道交界面面积。则物理量φ在冷却剂通道内满足控制方程:
(5)
其物理意义为:在单位时间间隔内,冷却剂通道内的物理量增量等于由于对流和扩散作用通过冷却剂通道间交界面的物理量的净值以及通道内源项产生物理量的总和。
相邻通道间的横向脉动流动将引起质量、动量和能量的扩散。在湍流搅混作用下,在相邻冷却剂通道交界面f处由P流向N和由N流向P的质量流速为W′PN和W′NP,如图2所示,则通道间净质量流速为0,即:

图2 冷却剂通道间横向流动示意图
W′f=W′PN=W′NP
(6)
Rogers和Tahir通过对不同几何形状的冷却剂通道间的湍流搅混进行研究[13-14],给出相邻通道间冷却剂质量流速W′f的计算关系式:
(7)
式中:μ为冷却剂动力黏度;DeP和DeN分别为通道P和N的当量水力直径;ReP为通道P中的雷诺数;s为相邻通道间交界面的宽度;K/Kg、b、r为常系数,对于正方形排布燃料棒束所形成的冷却剂通道其推荐值分别为0.002 5、0.9和0.894。则相邻冷却剂通道间由湍流搅混引起的物理量交换可表示为:
M′f·Sf=-W′fSf(φP-φN)
(8)
式中:M′f为物理量在通道间交界面的扩散通量,可表示为:
(9)
式中,PV为冷却剂通道中心间距。
据此,考虑湍流搅混的冷却剂通道内控制方程如下。
质量守恒方程:
(10)
动量守恒方程:
(11)
能量守恒方程:
(12)
式中:h为冷却剂比焓;M′M和M′E分别为动量和能量湍流搅混项,即冷却剂通道中由于湍流搅混而引入的动量和能量扩散作用;g为重力加速度;q为热流密度;t为时间;SE为能量源项,表征冷却剂与燃料棒表面的对流换热;SM为动量源项,包含由于燃料棒束、组件盒壁和定位格架等结构引入的摩擦和形阻压降。
控制体中,冷却剂流过燃料组件时的压降Δp为:
(13)
式中:L为控制体内的流动距离;De为流动方向的特征长度;f为阻力系数。
在燃料棒束区,对于层流和湍流,冷却剂纵向流动阻力系数分别按Hagen-Poiseuill公式[15]和Blasius公式[13]计算,其表达式为:
(14)
式中,Re为以冷却剂通道的当量水力直径为特征长度的雷诺数。
冷却剂横向流动阻力系数按Gaddis-Gnielinski公式[16]计算,其阻力系数的表达式为:
(15)
式中:Re为以燃料棒直径为特征长度的雷诺数;fl和ft分别为流动阻力中层流和湍流的影响因子,其表达式为:
(16)
(17)
式中:d为燃料棒直径;p为棒间距。
而在定位格架区,冷却剂受格架几何结构限制无横向流动,即横向流动阻力系数无穷大,而纵向流动阻力系数按推荐值为1.04。
1.2 燃料棒导热模型
假设单个控制体内所有燃料棒具有相同的热工状态。根据燃料棒结构特点将燃料棒沿径向划分N个节点,如图3所示。外侧两计算节点分别位于包壳内外两侧边界,其他计算节点沿燃料棒芯块中心向外侧布置且有一节点位于芯块边界。忽略燃料棒轴向导热,根据能量守恒定律,对于节点i有导热方程:
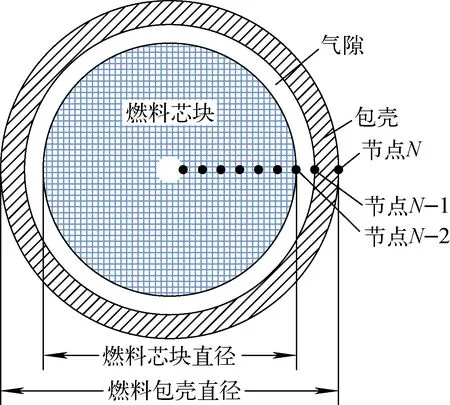
图3 燃料棒节点示意图
(18)
式中:ρi为节点i处材料密度;cp,i为节点i处材料比定压热容;Vi为节点i的等效控制体体积;Ti为节点i的温度;Qi-1,i为从节点i-1传导到节点i的热量;Qi+1,i为节点i+1传导到节点i的热量;Qi为节点i处单位体积释热率。
燃料棒内部节点间导热量通过节点间温差求得:
Qi-1,i=Ki-1,i(Ti-1-Ti)
(19)
Qi+1,i=Ki+1,i(Ti+1-Ti)
(20)
式中,Ki-1,i、Ki+1,i分别为节点i-1和i之间、节点i+1和i之间的等效导热系数,是热导率和燃料棒几何参数的函数。
Ki-1,i=Ki,i-1=
(21)
(22)
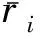
(23)
根据燃料棒的导热特点,可建立如下边界条件:1)燃料棒中心为对称边界,因此对于节点1的控制方程有K0,1=0;2)在燃料芯块与包壳之间存在间隙导热,此时QN-1,N-2=Hgap(TN-1-TN-2),其中Hgap为等效间隙导热系数,即KN-1,N-2=Hgap;3)在燃料棒包壳表面有Kf,N=HT,则Qf,N=HT(Tf-TN),其中Tf为冷却剂主流温度,HT为燃料棒与冷却剂之间的等效表面换热系数。
1.3 耦合换热模型
冷却剂通道控制体的加热功率来自与其内部包含的燃料棒表面的对流换热量:
(24)
式中:Q为冷却剂通道内的加热功率;Nb为该段冷却剂通道相邻的燃料棒总数;Qc,i和qc,i分别为燃料棒i表面的对流换热量和对流换热热流密度;Ai为控制体内燃料棒i的换热面积。
则该控制体内的能量源项可表示为:
(25)
式中:SE为能量源项;V为冷却剂通道的体积。
根据燃料棒导热模型假设,单个控制体内所有燃料棒表面与冷却剂的对流换热状态相同,则各燃料棒的对流换热热流密度可统一按牛顿冷却公式计算:
qc=hc(Tcs-Tf)
(26)
式中:Tcs为燃料棒包壳表面温度;hc为燃料棒包壳表面的对流换热系数,采用下式计算:
(27)
式中:λ为冷却剂导热系数;De为当量水力直径。
燃料棒包壳表面对流换热系数既影响冷却剂流动换热,又作为边界条件参与燃料棒导热计算,因此考虑耦合换热求解,具体步骤为:1)假定初始冷却剂流场和温度场,计算得到燃料棒包壳表面对流换热系数;2)以对流换热系数为边界条件求解燃料棒导热方程,获得燃料棒内部温度分布和表面温度;3)根据燃料棒包壳表面温度、冷却剂温度、换热面积和表面换热系数求得表面对流换热量;4)换热量作为冷却剂的能量源项代入流体控制方程中进行求解,获得冷却剂流场和温度场。将第4步得到的冷却剂流场和温度场重新代入第1步进行计算,反复迭代直至得到收敛结果。
2 数值模拟与结果分析
2.1 GE3×3实验
GE3×3实验是由美国通用电气公司所设计开展的燃料组件内冷却剂流动实验[17-18],该实验获得了不同工况下棒束通道内工质水的速度分布特性。实验段由呈3×3排列的9根燃料棒和正方形组件盒组成,如图4a所示。实验段总长为1 892 mm,组件盒边长为59 mm,边角采用半径为10 mm的圆角,燃料棒直径为14 mm,间距为19 mm。将网格节点布置于燃料棒中心,所建立的计算网格如图4b所示。

图4 GE3×3实验段(a)及网格(b)示意图
本文选取4组工况,分别采用CorTAF和COBRA程序进行计算。实验段压力为6.89 MPa,冷却剂入口温度为常温,入口速度分布均匀,分别为0.651、1.343、2.048和2.672 m·s-1。各工况下中心通道、边通道和角通道的冷却剂速度计算结果如图5所示。
由图5可见,同一工况内边通道和角通道内冷却剂受组件盒壁额外的摩擦影响,与中心通道相比流速较小。CorTAF程序计算结果与实验数据符合良好,表明该程序能有效预测燃料组件内冷却剂速度分布特性。CorTAF与COBRA程序间计算结果的偏差可能是由阻力系数关系式选取不同而导致,在相同硬件平台和求解设置下二者的计算相对误差和耗时列于表1,可见CorTAF程序在相近的计算精度下计算效率更高。

图5 GE3×3实验计算结果

表1 GE3×3实验模拟的误差和耗时
2.2 Weiss实验
Weiss实验是由美国西屋公司所设计开展的两个并联开式燃料组件内的冷却剂流动实验[19-20]。实验研究单个组件堵塞时两个并联开式燃料组件间的流量分配规律,实验段如图6a所示。
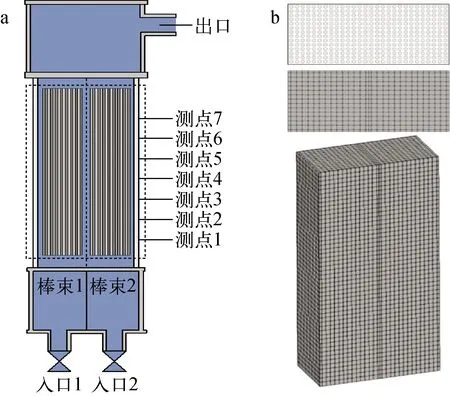
图6 Weiss实验段(a)及网格(b)示意图
实验段下部的两入口装有流量调节阀,通过控制冷却剂流量来模拟入口堵塞工况下两组件的流量差异。实验段内的燃料组件均含有呈14×14排列的196根燃料棒,工质在棒束通道中竖直向上流动。如图6a中虚线内区域所示,模拟中所选取的计算域为从组件入口到出口截面间的并联组件棒束通道,组件横截面及计算网格示如图6b所示。该实验工质为常温液态水,回路压力为常压,实验相关参数列于表2。

表2 Weiss实验段相关参数
选取Weiss实验中右侧组件入口部分堵塞工况进行模拟。左右两侧组件的冷却剂入口流速分别为3.52 m·s-1和1.76 m·s-1,流量占比分别为66.7%和33.3%。两组件内冷却剂流量占比的计算结果如图7a、b所示,并联通道内冷却剂流速在不同高度处沿水平方向的分布如图7c所示。在并联组件通道中左侧组件内的冷却剂通过组件间交界面流入右侧组件内,随流动发展组件间的冷却剂流量差异逐渐减小。可见计算结果与实验数据符合良好,表明CorTAF程序能有效预测入口堵塞工况下并联开式组件内流量分配特性。
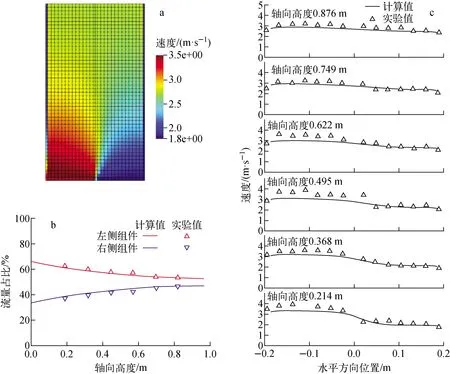
a——工质速度分布;b——两侧组件流量占比;c——水平方向速度分布
2.3 PNL2×6实验
PNL2×6实验是由美国太平洋西北实验室开展的棒束通道内冷却剂热工水力特性实验[21]。该实验通过设定燃料棒的功率分布,研究棒束通道内横向非均匀加热条件下的冷却剂流动换热特性。实验段为矩形组件盒,其中包含呈2×6排列的12根燃料棒,燃料棒采用电加热,冷却剂在实验段内竖直向上流动,在实验段的不同高度处共设有9个测量窗口,如图8a所示。模拟中所选取的计算域为加热段及其前后绝热段,组件横截面及计算网格如图8b所示。该实验的相关参数列于表3。
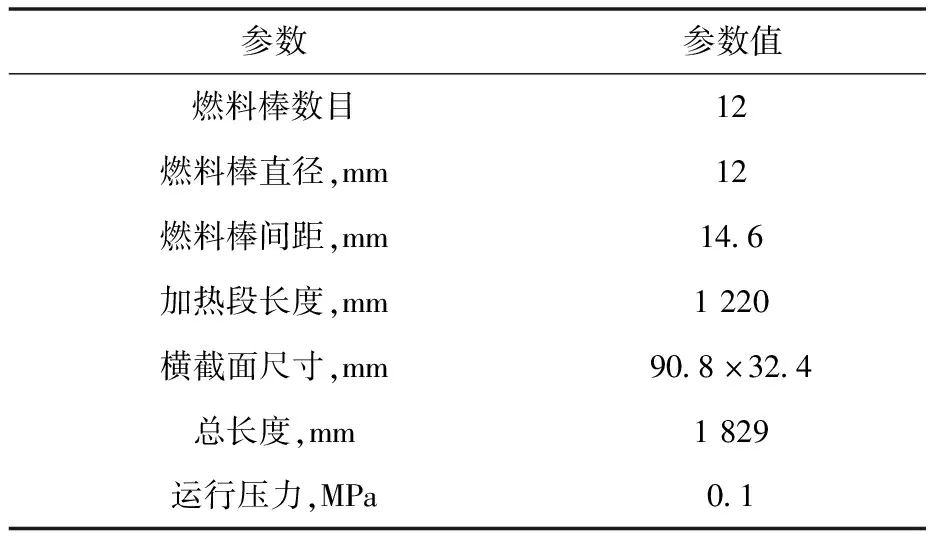
表3 PNL2×6实验段相关参数
本文选取1组稳态实验工况进行模拟。冷却剂入口速度和温度分别为0.1 m·s-1和285.15 K,运行压力为0.1 MPa,图8b中编号1~6燃料棒的功率为1.134 kW,编号7~12燃料棒的功率为0.567 kW。计算得到的实验段中心各通道内冷却剂的温度和速度横向分布如图9所示,其中还给出CUPID和MATRA程序的计算结果[22]。
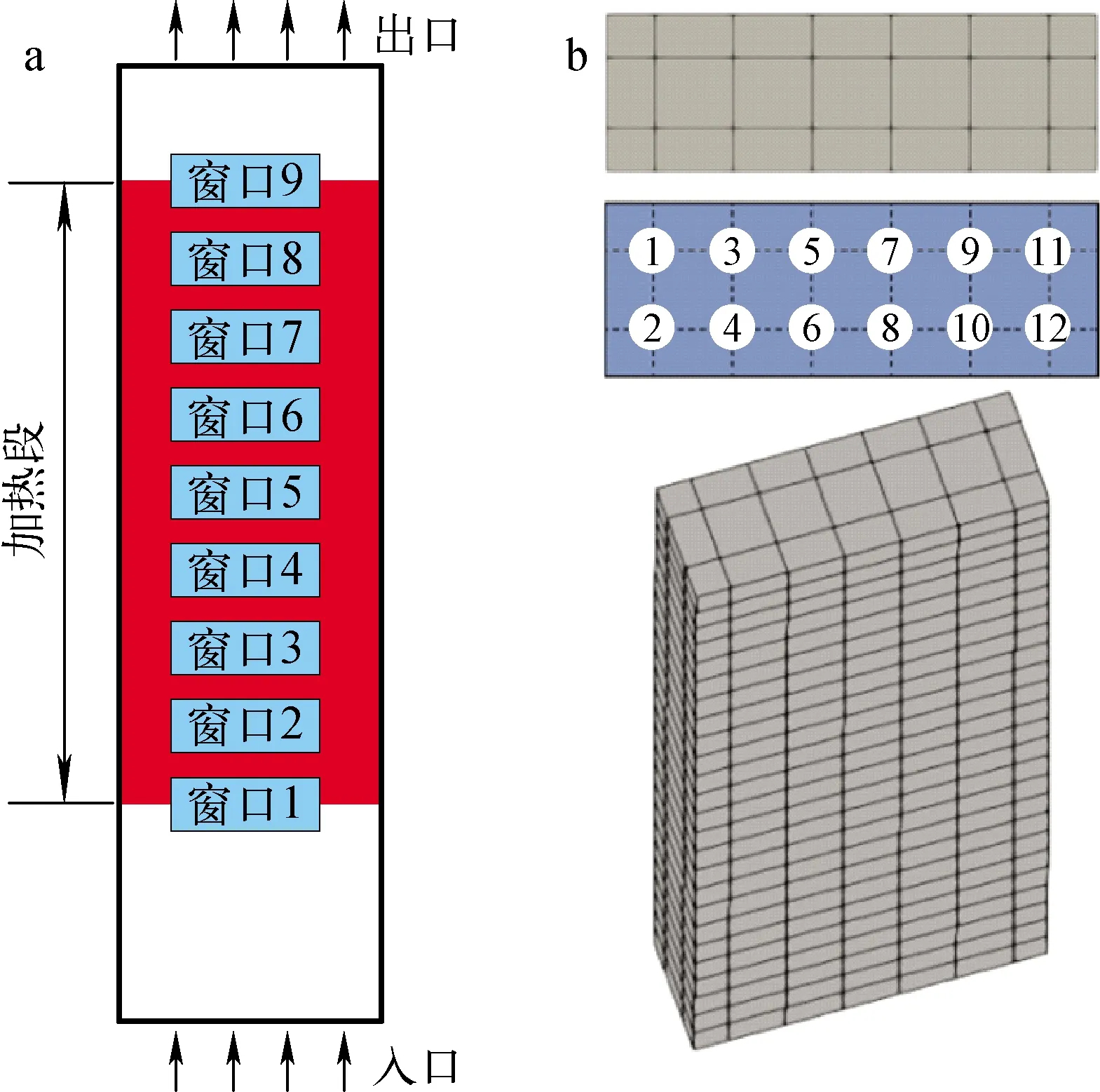
图8 PNL2×6实验段(a)及网格(b)示意图
由图9可见,由于燃料棒功率横向非均匀分布,冷却剂温度由高功率侧向低功率侧逐渐下降,受温度分布的影响,速度沿水平方向的变化趋势相同。CorTAF程序计算结果略低于实验数据,二者整体横向变化趋势相同,计算误差如图10所示,温度计算误差基本在5 K以内,速度计算误差基本在0.5 m·s-1以内,各程序计算结果均较为接近,表明CorTAF程序能获得棒束通道内横向非均匀加热条件下的冷却剂流动换热特性。

a——窗口3冷却剂温度;b——窗口3冷却剂速度;c——窗口7冷却剂温度;d——窗口7冷却剂速度

计算误差:a——冷却剂温度;b——冷却剂速度
对实验段进行流场精细建模的CFD模拟,得到窗口3和7处通道中心冷却剂温度水平方向分布,如图11所示。可见CorTAF程序计算结果与CFD精细建模计算结果整体较为符合,由于通道中心线上冷却剂温度和速度波动较大,分析误差来源可能是数据获取方法的差异:CorTAF程序计算获得的冷却剂温度为通道内平均温度,CFD精细建模计算获得的冷却剂温度为沿通道中心线的水平分布,而实验数据为测点处局部冷却剂温度,数据获取方法的差异导致三者间存在一定偏差。
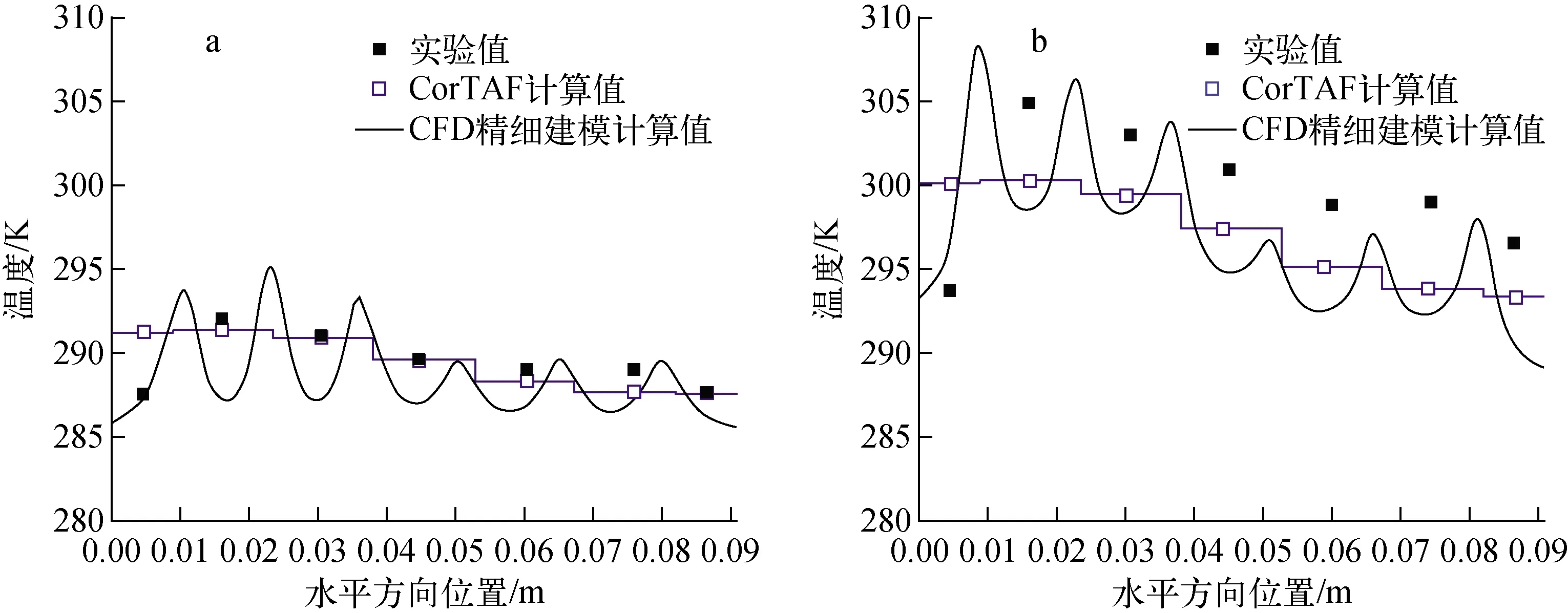
图11 窗口3(a)和窗口7(b)工质温度计算结果
3 结论
依托开源CFD平台OpenFOAM,针对压水堆堆芯棒束结构特点,建立了冷却剂流动换热模型、燃料棒导热模型和耦合换热模型,开发了一套基于有限体积法的压水堆全堆芯通道级热工水力特性分析程序CorTAF,主要结论如下。
1)选取GE3×3实验进行模拟,组件内各通道冷却剂流速分布的计算结果与实验数据符合良好,表明该程序能有效预测燃料组件内冷却剂流动特性。在相近的计算精度下CorTAF程序计算效率比COBRA程序更高。
2)选取Weiss实验进行模拟,组件冷却剂流量分布的计算结果与实验数据符合良好,表明该程序能有效预测入口堵塞工况下并联开式组件内流量分配特性。
3)选取PNL2×6实验进行模拟,中心各通道冷却剂温度和速度分布的计算结果与实验数据基本符合,与CUPID和MATRA程序计算结果较为接近,表明该程序能获得棒束通道内横向非均匀加热条件下的冷却剂流动换热特性,误差来源可能为数据获取方法的差异。
本文工作对压水堆堆芯安全分析工具开发具有参考和借鉴意义,后续将进行模型验证优化、全堆芯满功率稳态及事故工况瞬态热工水力特性分析,并依托OpenFOAM的优势开展核热耦合等研究。
