考虑临时和预约需求的共享泊位动态分配方法
2022-03-02刘永红罗霞胡剑鹏
刘永红,罗霞,胡剑鹏
(西南交通大学,交通运输与物流学院,成都611756)
0 引言
停车难是我国大城市普遍存在的问题。由于有限的城市用地,停车问题不能单纯地通过修建新的停车位来解决[1]。除了由于供需之间的不平衡之外,资源的低利用效率,尤其是在空间及时间上利用的不平衡,也容易造成“停车难”。因此,如何合理利用现有停车资源是停车管理的首要难题。
共享停车是利用不同土地开发强度下不同时段停车需求的差异,将泊位进行错时共享[2],能够有效提高停车泊位的利用率。居住区大多数出行均为通勤出行,在白天时段泊位多处于空闲状态,如果在白天时段将这些空闲的泊位资源共享出去,不仅有助于盘活现有的空闲停车资源,而且能够在一定程度上缓解停车紧张的问题。目前,共享停车泊位分配的研究从时间窗约束可分为两类。不考虑时间窗约束的研究主要有:ZOU等[3]以社会福利最大为目标,设计了一种泊位分配机制,可以激励驾驶员积极参与停车泊位分配过程并提交自己的真实停车信息;XIAO 等[4]通过引入Vickrey-Clarke-Groves(VCG)拍卖机制,并根据历史拍卖记录,对共享泊位进行分配;基于VCG 机制,通过物联网,
Price-compatible Top Trading Cycles and Chains(PC-TTCCs)和One-sided Vickrey-Clarke-Groves(OVCG)机制也被引入城市停车管理云平台中管理泊位[5];BOUDALI等[6]提出一种多准则的智能预订停车系统,通过优化驾驶员的停车偏好,对在线泊位进行实时分配;陈峻等[7]建立了由决策层和分配层组成的停车共享泊位动态分配模型,其上层构建了泊位共享的4类判断准则,下层预测停车泊位需求时变状态并进行动态分配。
考虑时间窗约束的主要有:SHAO 等[8]以停车系统收益最大为目标,建立共享停车泊位分配模型,并通过算例验证了模型的有效性;姚恩建等[9]基于具有颜色约束的加权顶点着色问题,建立了共享停车泊位资源优化配置模型;张文会等[10]建立共享停车泊位利用率最大化和步行距离最小化的双目标泊位分配模型,并采用粒子群算法求解多目标;CAI等[11]建立以拒绝数量最小,停车场收益、泊位占有率最大等为目标的两阶段泊位分配方法;ZHAO等[12]在停车位拥有者和停车需求用户到达、离去不确定情况下,建立了以数据驱动策略的停车泊位分配方法;JIANG等[13]在考虑了用户实际停车时间与提交的停车时间不一致以及业主不按时离开的停车不准时情景下,以期望收益最大为目标建立了0-1混合整数规划共享停车泊位分配模型;孙会君等[14]在综合考虑租用车位成本,提供停车服务收入及拒绝用户潜在损失的基础上,建立了以共享停车运营商利润最大化为目标的整数规划泊位分配模型;张水潮等[15]在考虑预约时刻、时长及延时需求的情景下,建立了以平台收益最大和步行距离最小的泊位分配双目标规划模型;何胜学等[16]在满足合理共享停车需求下,建立无人驾驶车位移成本最小的共享停车供需匹配模型,并设计了相应的模拟退火算法。
综上,现有研究对共享停车泊位分配模型目标、算法设计、应用场景等方面进行了探索,但对于同时存在临时共享停车需求和提前预约需求情形下,如何确立泊位匹配优先级;以及可通过历史数据预测未来时段的停车需求时,如何利用预测数据优化当前时段的泊位分配,从而延伸到所有时段的动态泊位分配缺乏研究。
在时间窗约束下,现有泊位分配模型研究多关注当前时段的供需,本文则利用滚动时域方法,在当前时段泊位分配时,同时考虑其未来几个时段的供需进行统一泊位匹配后,单独提取只属于当前时段供需结果,并将当前泊位分配结果反馈到下一时段,实现动态泊位分配。本文考虑临时停车需求和提前预约需求用户的特点,设计泊位分配优先级权重。同时,与同质处理拒绝用户的潜在损失不同,本文更加关注拒绝用户潜在损失的异质性。
1 居住区共享停车泊位分配模型
1.1 问题描述
居住区私家车位拥有者根据自己的使用特性,往往会提前一天通过向共享停车平台提交车位的空闲时间段及位置等信息的方式,将自己的车位暂时转让给平台,即可以认为一天内的共享停车供给是提前已知。对于停车需求用户,可以通过手机等设备在平台上提前预约或者临时发布自己的停车需求,因此,通常情况下共享停车平台获取的是当前时间段的共享停车需求,但是,可以根据共享停车需求历史数据,利用深度学习等预测方法得到未来几个时段的共享停车需求,即可以认为当前时段及其未来几个时段的共享停车需求已知。将一天划分为T个相等时段,假设当前时段为,本文研究的问题描述为:在已知所有时段的供给,当前时段t及直到其未来时段t+f的共享停车需求情况下,如何利用这些信息匹配当前时段的供需和如何将时段t的泊位分配结果反馈到下一时段t+1 掌握t+1,t+2,…,t+f+1 需求情形下的泊位分配中,实现对所有时段的动态泊位分配。共有临时停车和提前预约两类共享停车需求,基于运营商期望最大化地留住需求,同时,也保证一定的收益。在每个时段考虑泊位分配优先级时,对临时发布的共享停车需求需优先进行共享停车位匹配,因为这类停车用户可以等待平台匹配泊位结果的时间比较短,如果不优先对其进行泊位分配,用户很可能因为需要一定时间等待服务,选择放弃共享停车,从而对共享停车运营商造成一定损失;对于提前预约的共享停车需求,其发出需求的时间点(通过手机等设备在平台上提交需求的时间点)一般早于实际需要使用的泊位时间点,这些用户通常能够接受一定的时间等待服务,因此,这类用户的泊位分配优先级低于临时需求用户。
1.2 共享停车动态分配模型
1.2.1 共享停车供给

图1 共享停车供给转化为0-1向量示意Fig.1 Schematic diagram of transformation of shared parking supply into binary variables

1.2.2 共享停车需求


1.2.3 单时段共享泊位分配









图2 单时段泊位分配Fig.2 Schematic diagram of slots allocation for single time interval
1.2.4 泊位动态分配流程
将未来时段的供需考虑到当前时段的泊位分配中,目的是在动态分配中利用多时段优化取代单时段优化,且通过此操作可能将当前时段的某些供给预留给未来时段的某些需求能够使整体泊位分配更优。在利用滚动时域对下一时段t+1 进行泊位分配时,需要更新供给与需求。共享停车需求的停车时段是连续且唯一的,其需求矩阵可以直接进行更新,即

单个共享停车供给在一天内可能存在多个供给时间段,对供给矩阵进行更新时,需减去t时段泊位分配后占用的泊位供给,得到剩余的泊位供给为

由此得到下一时段t+1 的泊位供给矩阵为为

综上,即可完成一定时间内共享停车供给和需求的动态泊位分配,本文构建的共享泊位动态分配流程如图3所示。
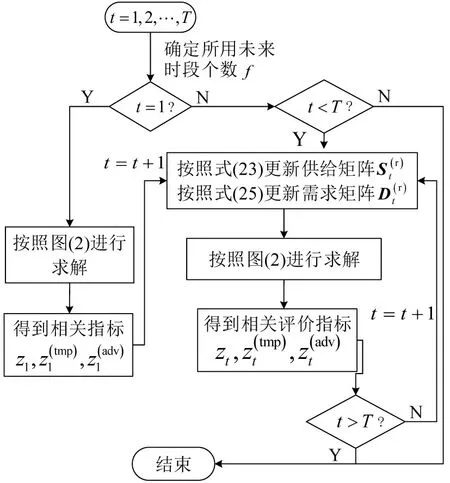
图3 共享泊位动态分配流程Fig.3 Flow chart of dynamic shared parking spaces allocation


1.2.5 评价指标

2 算法



3 共享泊位分配实例
为验证共享泊位动态分配模型的有效性和合理性,选择来源于成都共享停车APP(私家车位APP)2018年11月1日的数据对模型进行实证研究。包含3个居住小区,总的供给和需求量分别为79 和72。部分共享停车供给和共享需求信息如表1所示,其中,“*”为隐私信息。在进行模型验证时直接将实际需求假设为需求的预测。
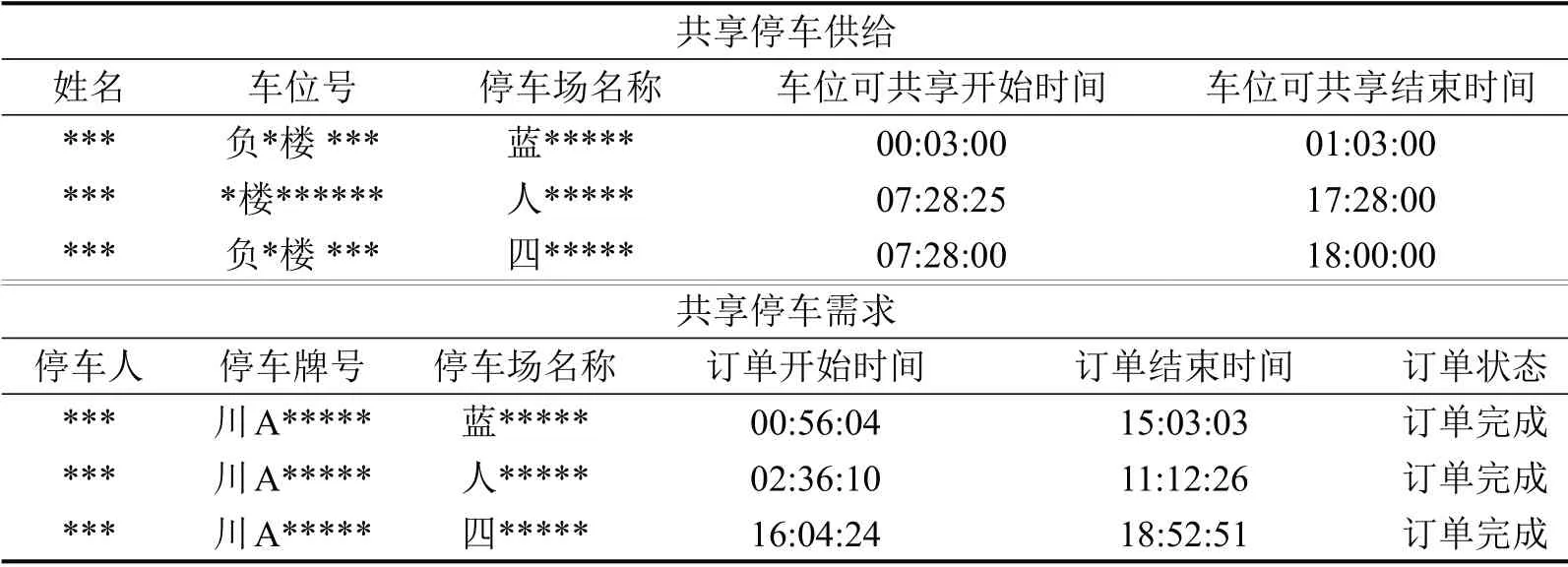
表1 模型验证所用数据样本Table 1 Sample data for model demonstration
各停车场距离目的地距离分别为915,696,518 m,停车费率分别为1.00,1.35,1.12 元∙h-1。f取值设为3,w2=1(w1>w2是为保证可以对临时共享停车需求进行优先泊位分配)。为便于描述,用停车场1、停车场2 及停车场3 表示3 个共享停车场,临时共享停车需求的目标用目标1表述,提前预约共享停车需
求的目标用目标2表述。
3.1 单个研究时段长度对泊位分配的影响
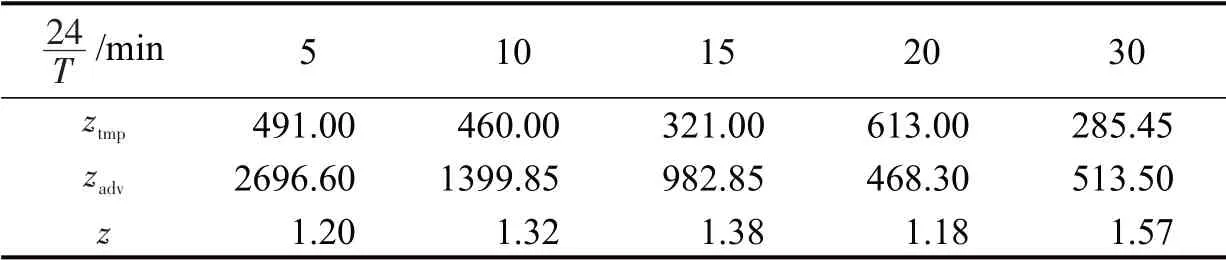
表2 不同研究时段长度下泊位分配后的目标值Table 2 Target value after slots allocation under different time intervals length
从表2和图4可以得出:
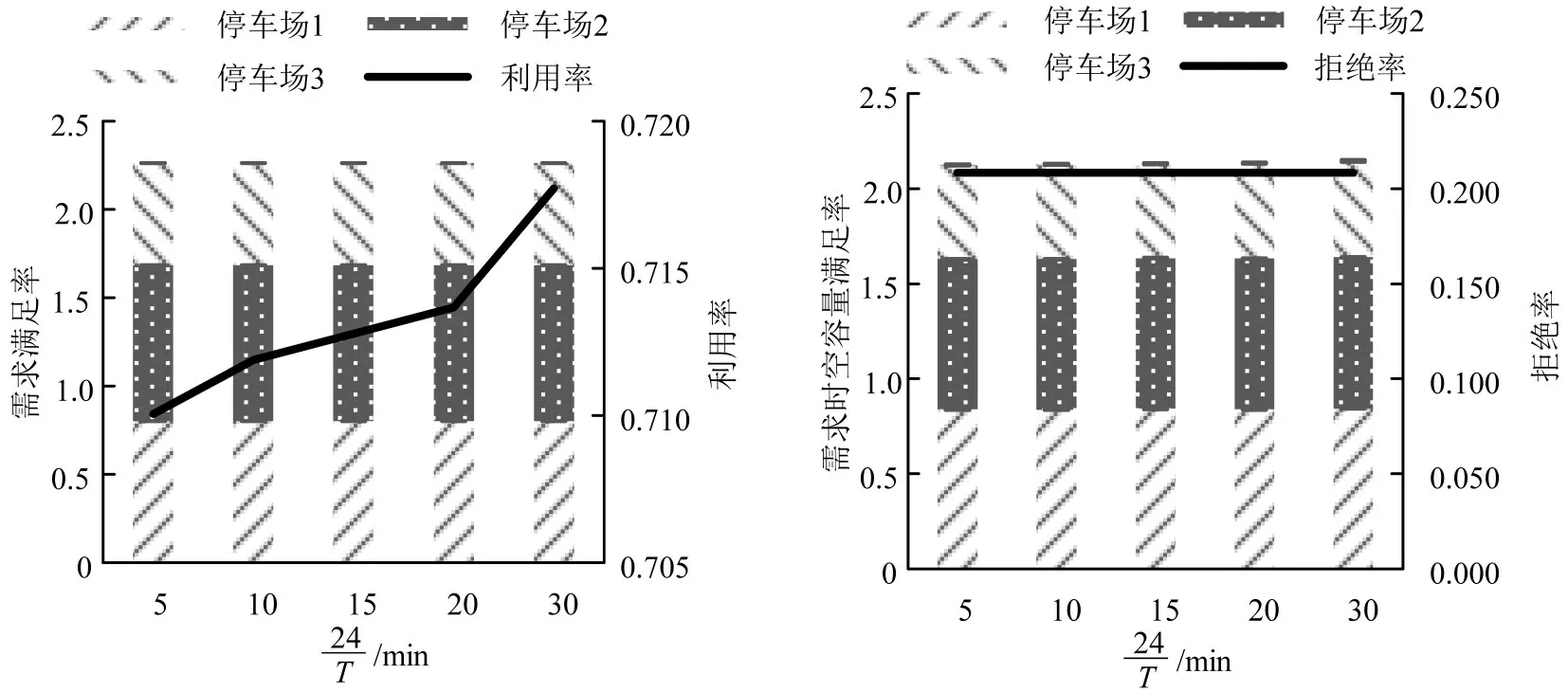
图4 不同研究时段长度下泊位分配后的评价指标Fig.4 Evaluation index after slots allocation under different time intervals length
3.2 临时和提前预约停车需求比例对泊位分配的影响
为研究临时停车需求和提前预约停车需求比例对共享泊位分配的影响,将T设为24,f设为3,临时共享停车需求所占比例的取值从0~1 变化,其他参数设置同上。泊位分配后的目标值和评价指标的结果如表3和图5所示。
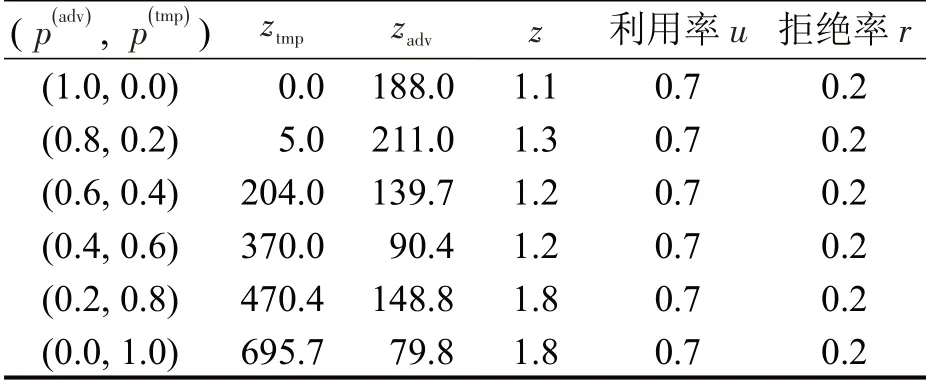
表3 不同临时共享停车需求比例下泊位分配后的结果Table 3 Results after slots allocation under different temporary shared parking demand ratios
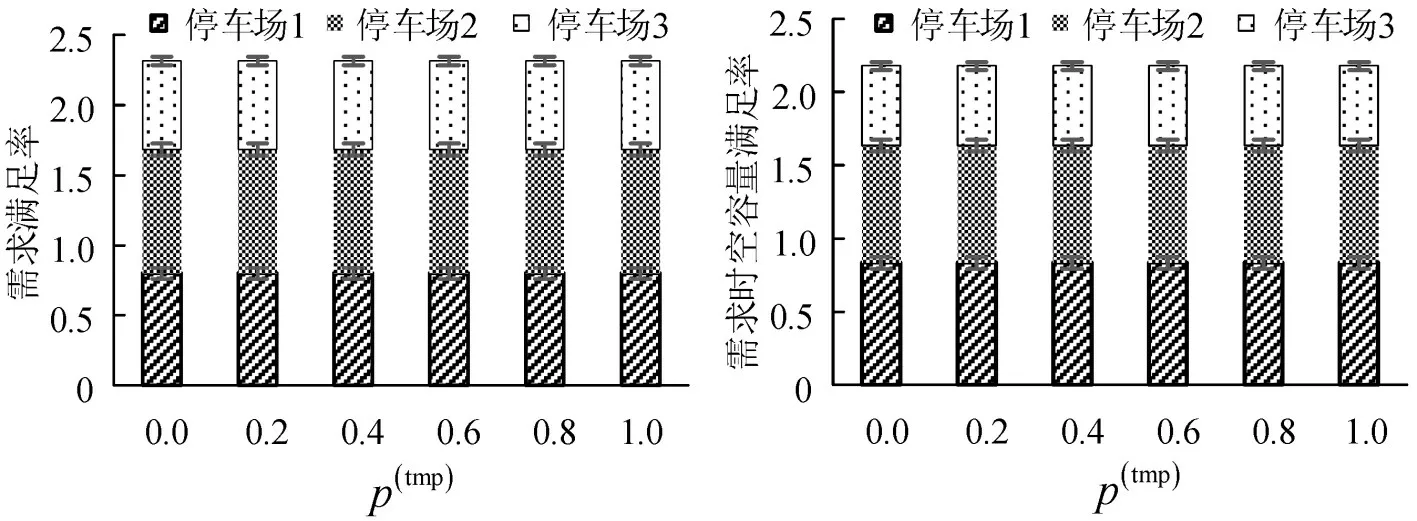
图5 不同临时共享停车需求比例下泊位分配后的评价指标Fig.5 Evaluation index after slots allocation under different temporary shared parking demand ratios
从表3和图5可以看出:
3.3 未来时段的数量f 对泊位分配的影响
为研究将当前时段的未来几个时段的供给和可预测的需求同时考虑的情况下对泊位分配效果的影响,将T设为24,设为0.5,变化f的取值,其他参数设置同上。不同f取值下目标值和评价指标的变化情况如表4所示。
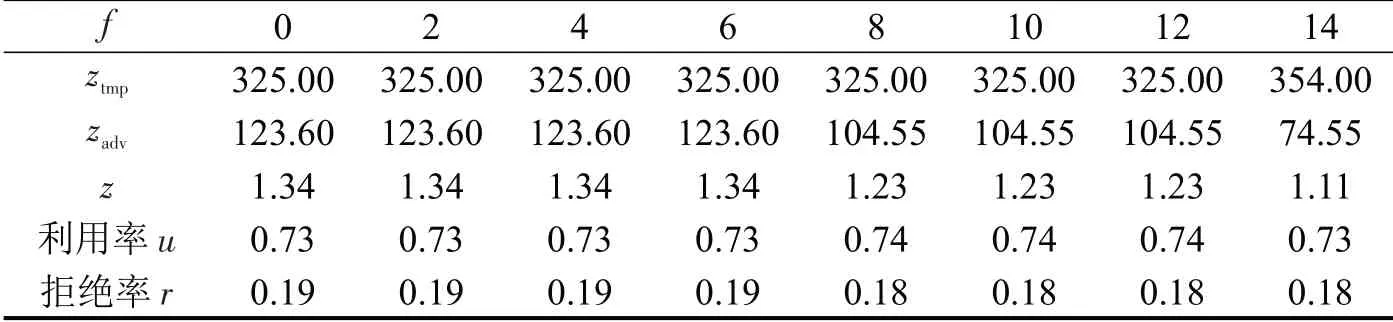
表4 不同f 下泊位分配后的结果Table 4 Results after slots allocation under different f
从表4 可以得出,归一化后的目标2 对f的变化较为敏感,随着f的增大,总目标逐渐减小,整体结果逐渐变优,当f取14 时,对比f为0 时,总目标优化了17.2%。因此,可以得出在泊位进行分配时,考虑未来几个时段的供给和需求会使泊位分配效果更好。为进一步验证本模型所考虑的f的有效性,将需求在原有基础上增加80%,当f取14时,总目标对比f取0 时优化了13.7%。需求扩大后和需求不扩大时对应的归一化目标和评价指标的变化情况如图6所示。
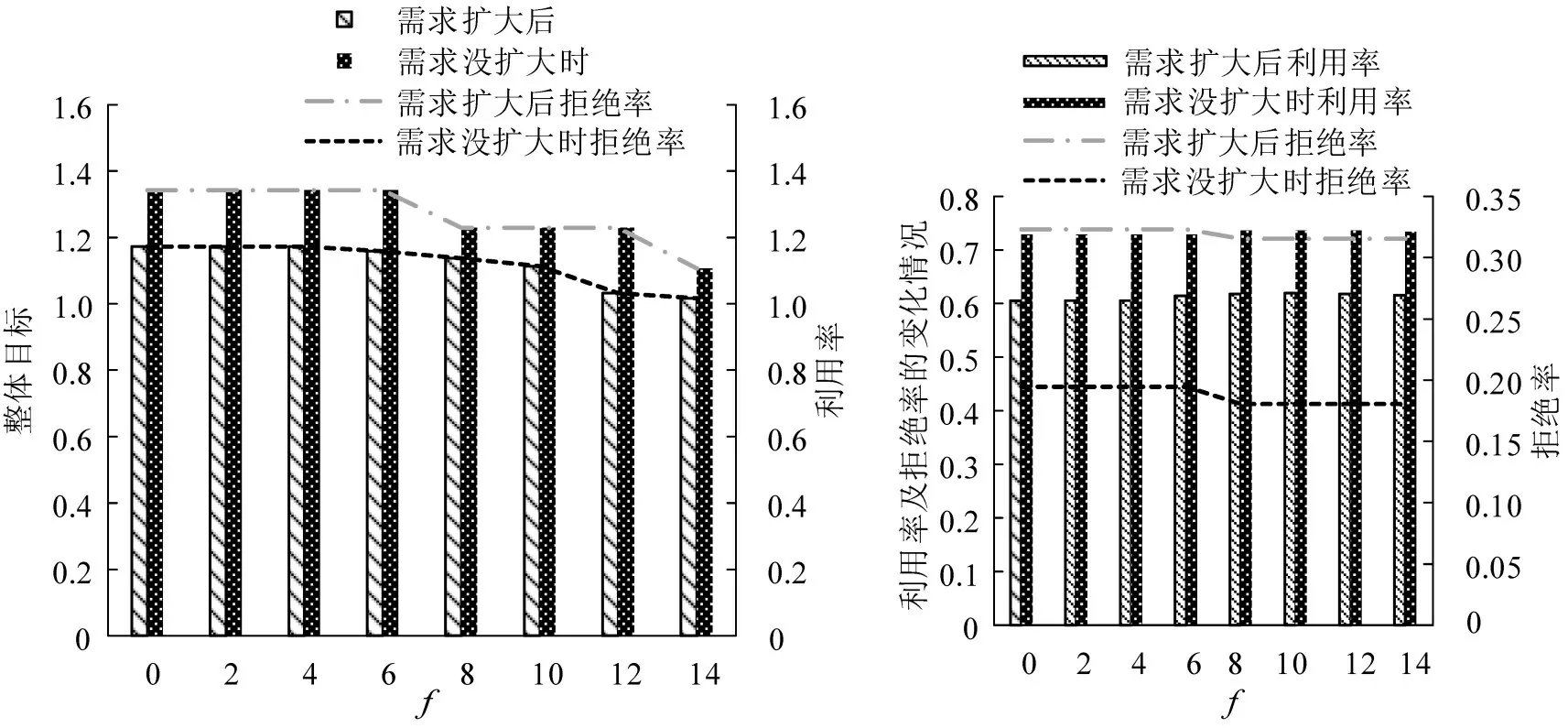
图6 扩大和不扩大需求后改变f 的结果对比Fig.6 Comparison of results of changing f after expanding and not expanding demand
从图6 可以看出,在这两种情况下,随着f的增大,总目标越优。此外,随着f的增大,共享停车供给的利用率逐渐增加,共享停车需求的拒绝率都有不同程度的减小。进一步验证了本文所提出的将未来几个时段供需考虑到当前时段进行泊位分配的合理性。
3.4 惩罚系数对泊位分配的影响
为比较目标1和目标2的惩罚系数对泊位分配的影响,分别将η1和η2的取值固定,变化η2及η1,其他参数取值同上,其结果如图7所示。
从图7可以得出,当固定一个拒绝停车需求的惩罚系数,改变另一个惩罚系数时,固定的惩罚系数对应的目标变化幅度较小。此外,对比图7中固定η1和η2的结果,当η2固定时,系统整体扰动(包括目标1、目标2及总目标的变化)相比固定η1时更小,得出η2的变化相比η1的变化对整个泊位分配系统影响更为明显,因此,在泊位分配中整体优化目标对η2更为敏感。
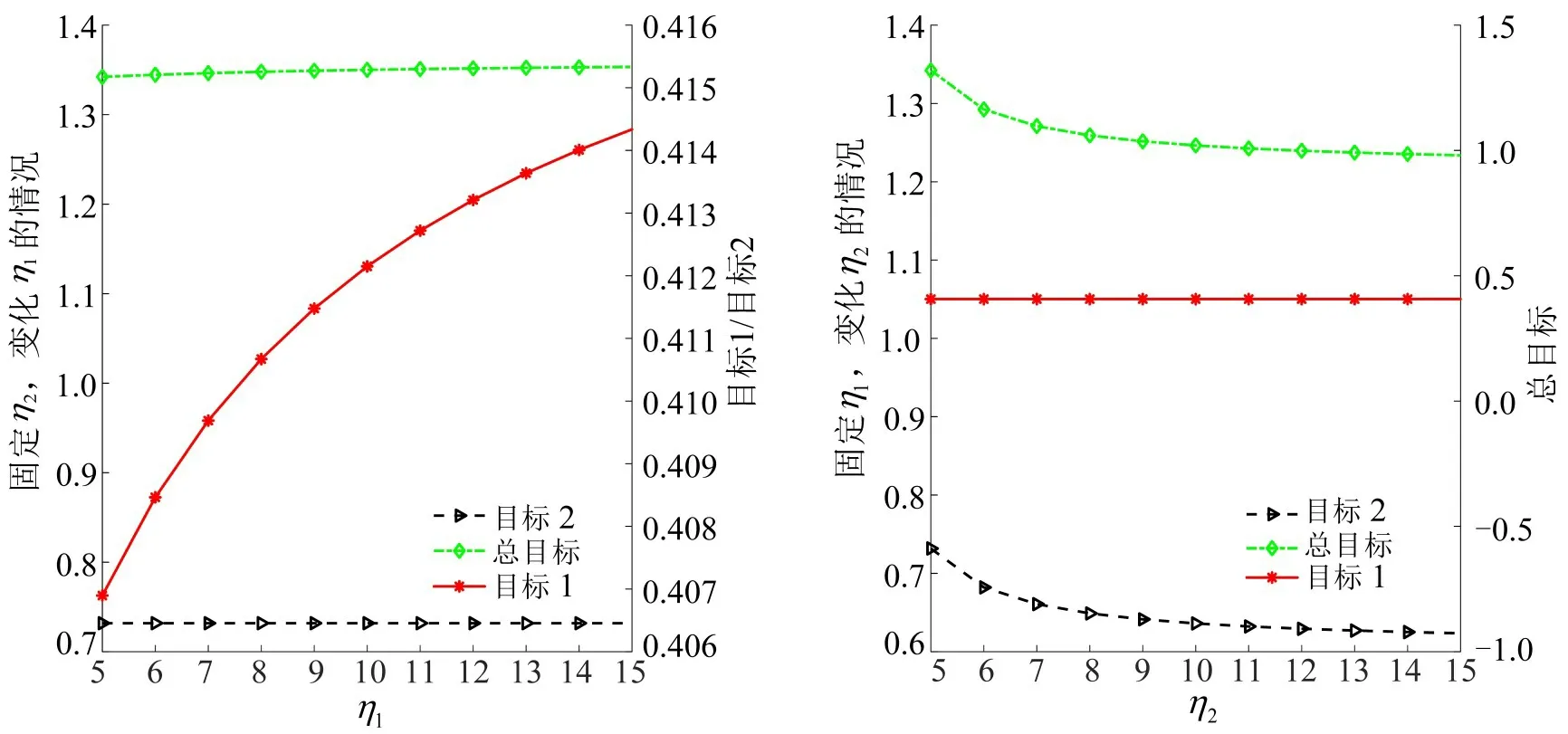
图7 η1 和η2 单独变化时的目标值Fig.7 Target value when η1 and η2 change separately
3.5 目标归一化的权重系数对泊位分配的影响
在前面的所有实验场景中,为保证临时共享停车需求可以优先分配到泊位,w1都是设为1.5,w2设为1,为进一步验证w1和w2的相对关系对泊位分配的影响,将w2和w1分别设为1,变化w1、w2,其他参数同上,得到不同取值下泊位分配效果如图8所示。
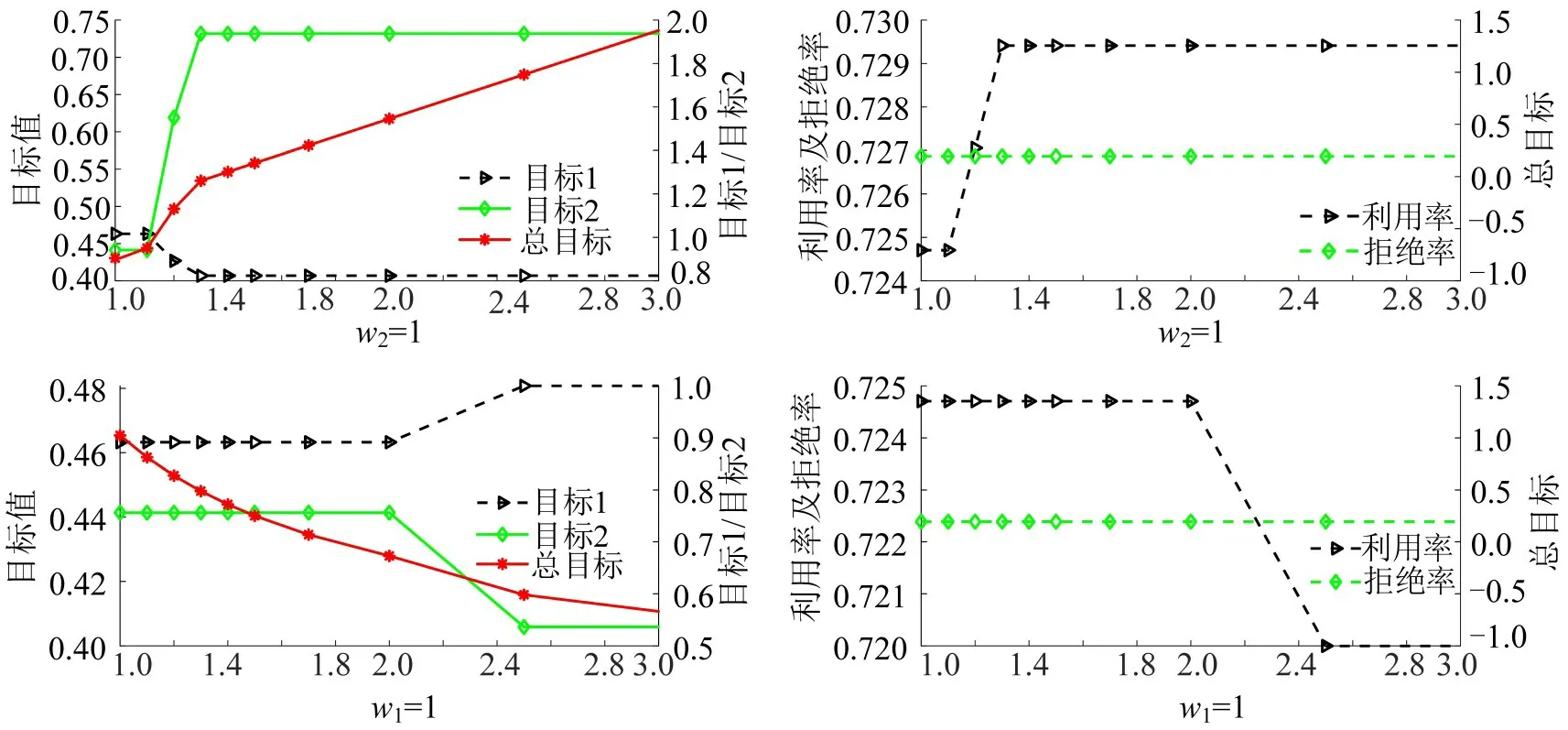
图8 w1 和w2 相对变化时的目标值Fig.8 Target value when ratio of w1 and w2 changes
从图8中可以得出:
4 结论
用率在某个区间范围有较小幅度的波动,而拒绝率基本保持不变。因此,在这种情况下,利用率对于w1和w2的相对大小关系具有弱相关性,而拒绝率与两者的相对大小关系基本不存在相关性。
本文建立了同时存在临时和提前预约共享停车需求的多居住区共享停车场泊位分配双目标规划模型,在此基础上提出了共享停车泊位的动态分配方法。选取泊位利用率、需求拒绝率、需求满足率、需求时空容量满足率指标对模型的有效性进行验证。研究结果表明:
(1)临时和提前预约共享停车需求比例大致相当时,会使泊位分配后总目标最优;
(2)将未来时段的供需考虑到当前时段的泊位分配中,会使泊位分配总目标更优,考虑的未来时段数量越多,泊位分配效果越好;
(3)提前预约停车需求的拒绝惩罚系数对整个泊位分配影响较临时停车需求的拒绝惩罚系数大;
(4)增加提前预约停车需求部分的权重,总目标更优。
