基于形态滤波与AVMD的滚动轴承故障诊断研究
2022-03-02李劲涛
李劲涛
(吉林铁道职业技术学院,吉林 132000)
0 前言
滚动轴承作为机械设备的最基础关键零部件被广泛应用于军事、工业和农业的生产[1-3]。滚动轴承的损伤是机械设备最常见的故障原因之一,将直接导致机械系统无法正常运行。当轴承发生局部故障时,会产生周期变化的脉冲信号。由于在检测这些脉冲故障过程中经常受到强噪声的影响[4,5],因此,如何从强背景噪声中提取轴承故障信息至关重要。
变分模态分解方法是一种自适应的非递归信号处理方法[6]。现有研究中,VMD的系统参数模数和惩罚因子通常以人为经验选择,没有考虑模数和惩罚因子之间的相互作用对VMD分解结果的影响。文献[7]研究表明,QPSO可以有效地改善局部最优解的问题。因此为了获得VMD分解方法的最优参数,采用QPSO方法对VMD的参数进行优化。尽管VMD方法可以有效地分解信号,但不适用于处理背景噪声较强的信号[8,9]。由于在测量过程中不可避免会产生背景噪声,有必要对原始信号进行去噪。近年来形态滤波被广泛应用在机械振动信号领域,是一种有效的非线性和非平稳信号的滤波器[10-13]。因此,本文提出了一种基于MF和AVMD方法的混合故障诊断方法。
1 基本理论
1.1 VMD
VMD是一种非递归信号分解方法。其目的是将输入的实信号f分解为一系列子信号组合,并且分解后的模式uk在频域中具有特定的稀疏性。每个模式包含一定的长度带宽和中心频率ωk。带宽受平衡因子α的影响,并且均匀地分布在中心频率ωk上。
约束变分问题定义为
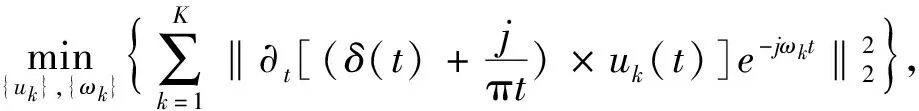
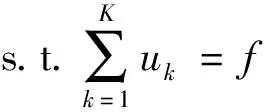
(1)
二次惩罚项α和拉格朗日乘子λ可以将上述最优问题变成非约束变分问题。然后,广义拉格朗日函数可描述为
L({uk},{ωk},λ)=


(2)
首先预先设置分解模式的数量K和平衡参数α。式(2)的鞍点通过乘数的交替方向方法(ADMM)找到。然后模数和中心频率ωk由式(3)和式(4)迭代更新得到。
(3)
(4)

1.2 QPSO
在量子空间中,粒子的状态由波函数ψ(x,t)描述。通过求解薛定谔方程来获得粒子在空间中某个点的概率密度函数,然后通过蒙特卡洛随机模型得出粒子的位置方程,即
(5)
Pid=φ·Pbestid+(1-φ)·gbestd
(6)
(7)
式中,u和φ分别是从0到1的随机数;Mbest为平均最佳位置;Pid为第i个粒子的局部最优值;向量Pbestid表示第i个粒子在迭代后到达的最佳位置;向量gbest是种群到达的最佳位置;N表示粒子总数;L为势阱的特征长度,即粒子的搜索半径,可以用式(8)进行描述。
L=2β|Mbestd-xid(t)|
(8)
(9)
式中,β是用于控制算法收敛速度的设计参数,取值范围是0.5~1.0。
将式(7)和式(8)代入式(5)。粒子的位置更新策略定义为

(10)
式中,rand()是0到1的随机数。
1.3 权重峭度指标
目标函数的选择会影响VMD系统参数的优化结果,峭度指数对冲击信号特别敏感。
(11)

(12)
考虑到两个测试指标的特点,构建了综合权重峭度指标作为自适应VMD参数优化的目标函数,其表达式为
KCl=Kr·|C|
(13)
最终QPSO优化VMD得到的目标函数为
(14)
式中,KCli(i=1, 2,…,k)是VMD分解模式ui的权重峭度指标;k和α是被优化的参数组,本文k的优化范围是2到8,α的优化范围是1 000到10 000。
2 MF-AVMD测试方法
2.1 形态滤波消噪
假设输入的原始信号f(n)是一维离散函数,其定义域F=(0,1,…,N-1);结构元素g(m)也是一维离散函数,其定义域G=(0,1,…,M-1),并且N≥M。四种基本算子定义如下:
(f⊕g)(n)=max[f(n-m)+g(m)]
(15)
(fΘg)(n)=min[f(n+m)-g(m)]
(16)
(fog)(n)=(fΘg⊕g)(n)
(17)
(f•g)(n)=(f⊕gΘg)(n)
(18)
式中,⊕表示膨胀算子;Θ表示腐蚀算子;o代表开算子;•表示闭算子。
由于形态滤波是一种良好的非线性信号处理方法,并且具有结构形式简单,计算效率高的特点。因此为了进一步处理信号的强背景噪声干扰,一种组合形态顶帽变换的滤波算子被提出[14,15],即
(19)
2.2 MF-AVMD的滚动轴承故障诊断方法的技术路线
MF-AVMD的滚动轴承故障诊断方法的流程图如图1所示,其工作步骤如下:

图1 提出方法的结构框图
(1)获得振动测试信号y(t)。
(2)根据权重峭度指标选择MF的参数,然后对原始信号进行滤波。
(3)设置VMD系统参数(模数k和惩罚因子α),初始化QPSO优化参数。
(4)判断是否达到迭代条件,选择最佳的优化参数。
(5)利用最优的参数进行VMD分解,获得最终的故障诊断研究结果。
3 实验验证
为了验证该方法的有效性和工程适用性,对轴承的内圈故障进行了测试。测试实验台如图2所示,该实验台包含2马力的电动机、变频器、控制开关、计算机、数据采集器、加速度传感器、测试轴承和测试系统。轴承的具体结构参数如表1所示。电机的转速为1 200 r/min,设备采样频率为16 384 Hz,采样点数为16 384。轴承的内圈故障频率计算如下:

表1 滚动轴承的几何参数
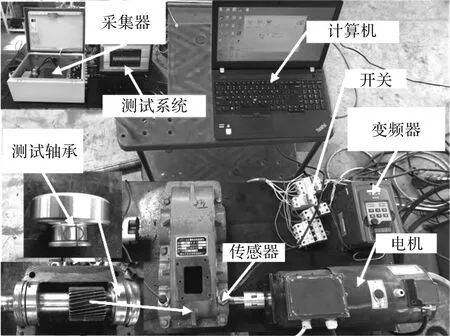
图2 轴承测试实验台
(20)
由传感器收集到的振动信号时域图如图3a所示,傅立叶变换后的频域图如图3b所示。在图3b中,轴承的故障特征频率污染严重无法被识别。为了验证提出方法的有效性,分别采用AVMD和MF-AVMD方法对实验信号进行处理。首先采用QPSO优化系统参数,得到的优化结果如图4所示。从图中可以看出随着迭代的数量增加,两种算法的KCl值倾向于稳定。对于AVMD方法,优化的最优模数k为5,惩罚因子α为2 000,最大KCl值为2.049。对于MF-AVMD方法,优化的最优模数k为4,惩罚因子α为1 000,最大KCl值为2.215。两种方法的优化结果进行比较,具有最大KCl值的MF-AVMD方法在提取轴承故障特征方面优于AVMD方法。为了进一步验证结论,用两种方法对实验信号进行更深入的分析。

图3 实验信号的时域图和频域图

图4 AVMD和MF-AVMD的QPSO收敛曲线结果
首先采用AVMD方法处理图3a中的时域信号,分解后得到的时域结果如图5a所示。在计算KCl的数值结果表明模数u3是最敏感模数。由所获得的频域计算结果图5b来看,轴承内圈的故障频率集中在模数u3中。图5中只能检测到故障频率fi及其2倍故障频率2fi,其它高阶故障频率无法被识别。转频fr因低频噪声干扰严重不能清楚地被检测到。

图5 AVMD方法处理的实验结果
采用MF-AVMD方法分析振动实验数据,得到的时域和频域结果分别如图6a和图6b所示。优化的最佳k值为4,最敏感模数依然为u3。在图6b的u3中,可以清楚地识别转频fr,故障频率fi及其高阶故障频率(2fi、3fi和4fi)。此外,fi和其高阶故障频率的周围出现2倍转频的边频带,这表明故障频率被转频所调制。比较结果表明所提出的方法能够更好地提取轴承故障特征和抑制背景噪声干扰。证明了MF-AVMD方法的有效性和优越性。

图6 MF-AVMD方法处理的实验结果
图7列举了两种方法所有模数的KCl值。图中MF-AVMD方法中最敏感模数的KCl值为2.215,AVMD方法中最敏感模数的KCl值为2.049。对比结果进一步表明MF-AVMD方法在提取滚动轴承故障特征上优于AVMD方法。

图7 AVMD和MF-AVMD中模数的KCl值比较结果
4 结论
针对传统方法凭经验选择VMD系统参数的问题,提出了一种基于QPSO的参数自适应VMD的方法来提取滚动轴承的故障特征。该方法可以自适应地获得最佳的VMD系统参数。此外,为解决故障特征被强背景噪声淹没的问题,提出了一种CMFH形态滤波去噪方法。实验测试结果表明,本文的方法能够有效地从背景噪声中提取滚动轴承的故障特征,比较分析结果表明MF-AVMD方法要优于AVMD方法。
