阀控非对称液压缸自适应非线性控制研究

2022-03-02郭丽丽赵文川

重型机械 2022年1期

徐威，郭丽丽，梁全，赵文川

(沈阳工业大学机械工程学院，辽宁沈阳 110870)

0 前言

电液伺服系统因其功率密度大、响应速度快等优点而在工业生产、重型机械以及医疗器械等领域有着广泛应用，而非对称液压缸具有体积小、维护成本低以及环境适应性强等特点。因此，对其控制策略研究具有重要意义[1-3]。传统的控制方法多采用线性化处理方法[4]，但非线性控制策略的控制效果更好。

应用非线性控制，首先要建立阀控非对称缸的非线性数学模型。目前国内外学者进行了很多研究。其中，曾乐在文献[5]中论述了电液比例阀控非对称缸系统的负载流量特性，指出了非对称缸正反方向运动特性不一致的特性，但没有解决非对称缸的控制问题。柏艳红在文献[6]中建立了阀控非对称缸的仿真模型，但其采用的是在工作点附近的线性化方法，相比非线性模型有一定程度的误差。本文综合前人的研究成果，推导出涉及内泄漏的阀控非对称缸的非线性数学模型。

研究控制系统，建立控制算法数学模型，需要注意的是，非线性控制系统相较复杂，并存在全部或部分参数未知，则非线性控制往往需要与自适应控制相结合。在非线性控制领域中，具有代表性、广泛性应用的方法是反步法。20世纪90年代，Krstic M等人[7]提出了一种处理非线性问题的方法——反步法，该方法得到了广泛的应用[8]。在自适应控制领域，文献[9,10]用输出反馈的方法实现了对液压缸的自适应控制，该控制主要适合只有位移输出已知的情况；文献[11,12]采用自适应反步法研究阀控缸系统的位移和受力控制。另外，学者Yao[13-15]采用投影法和反步法相结合，进行非对称缸的控制算法设计。在综合参考上述文献的前提下，由于本文所研究的阀控缸系统所有状态已知，而部分参数未知，因而适合采用自适应反步法进行控制。

验证控制算法需要通过仿真，由于功率键合图能够适合对电液系统进行仿真，因此，国内外很多学者对其在液压控制系统中的仿真进行研究[16-18]。其中文献[19]介绍了带有长管道的电液伺服系统功率键合图建模和仿真方法。文献[20]介绍了利用功率键合图进行液压绞车的控制系统设计。为了更好的验证所开发的自适应控制算法，则本文也采用功率键合图建立阀控非对称液压缸的仿真模型，以验证控制算法。

通过对比前人的研究，本文推导了阀控非对称缸的非线性数学模型，利用反步法进行了自适应控制器的设计，再根据建立的阀控非对称缸的功率键合图模型，进行算法的仿真验证，并给出控制算法的参数整定方法，具有重要意义。

1 阀控非对称缸系统动态特性

1.1 假设条件

要对非线性系统进行控制，首先要得到该系统的数学模型，即使非线性控制能描述许多实际的复杂问题，但推导阀控非对称液压系统动态特性方程时，仍然要对系统做适当的简化，忽略一些次要因素，抓住主要矛盾，这是工程应用中常采用的方法。因此，为了推导其非线性动态特性方程，特做如下假设[20]：

(1)阀为零开口匹配对称四通滑阀；

(2)所有管道都短而粗，流体质量影响和管道动态忽略不计。

另外，定义变量液压缸左右两腔面积比、负载压力、负载流量分别为

α=A2/A1

(1)

pL=p1-αp2

(2)

(3)

式中，A1、A2为左右两腔有效面积；Q1、Q12分别为左右两腔流量；p1、p2为液压缸左右两腔压力。

1.2 滑阀的流量方程

阀控非对称缸动力机构原理图如图1所示。

由于非对称缸具有动态不对称性，因而液压缸活塞正、反向运动时，其方程是不一致的。

当活塞运动速度为y>0(xv>0)时，流入液压缸左腔流量为

(4)

流出液压缸右腔的流量为

(5)

整理公式(1)、(2)得到正向运动时负载流量和液压缸流量为

(6)

(7)

当活塞运动速度为y<0(xv<0)时，流出液压缸左腔的流量为

(8)

流入液压缸右腔的流量

(9)

同样结合公式(1)、(2)，整理得到反向运动时

(10)

(11)

从公式(6)、(7)、(10)和(11)可以看出，非对称缸正反向运动时，其负载流量和两腔的压力是不同的，印证了其非对称性的特点。

1.3 液压缸流量连续性方程

不失一般性，忽略外泄漏，则液压缸无杆腔流量连续性方程为

(12)

有杆腔的流量连续性方程为

(13)

式中，V1、V2为液压缸左右两腔体积；cli为内泄漏系数。另外，液压缸左右两腔体积定义公式为

V1=V01+A1y

V2=V02-αA1y

(14)

式中，V01、V02为左右两腔初始容积；y为液压缸位移。考虑到A1y≤V01,αA1y≤V02，整理公式(3)和(7)得到简化表达式为

(15)

(16)

1.4 动力机构的力平衡方程

液压缸的力平衡方程为

(17)

式中，m为负载质量；B为负载粘性摩擦系数；K为负载弹簧刚度；Fg为外负载力。

1.5 伺服阀的动态特性

根据文献[8]，伺服阀的动态特性可以近似为一阶惯性系统，为

(18)

式中，T为伺服阀的时间常数(可从伺服阀手册样本中查得)；k为伺服阀增益；i为输入伺服阀电流。

1.6 阀控非对称缸非线性特性方程组

(19)

(20)

从式(19)和(20)可以看出，正反两个方向运动时，只有第3个方程是不同的。

为了推导后面的自适应算法方便，将方程(19)改写为

(21)

同样，方程(20)也可以改写成类似的形式，只是第3个方程稍有不同，为节省篇幅，只列写第3个方程为

(22)

2 控制器的设计

反步设计法是交叉选择李雅普诺夫函数与反馈控制的递归过程，是将整个系统的设计问题分解为一系列低阶子系统的设计问题。利用低阶子系统存在的额外自由度，反步设计方法能在与其他方法相比更宽松的条件下求解稳定控制、跟踪控制和鲁棒控制问题，同时，反步法也特别适合进行自适应控制[20]。

如前文所述，阀控非对称液压缸的非线性模型具有对称性，因而其控制器的设计也具有非对称性，应该分情况考虑。

当xv>0时，

(1)反步法第1步。令i=1，定义误差为

e1=x1-x1,d

(23)

则

(24)

令李雅普诺夫函数为

(25)

其导数为

(26)

当

(27)

时，有

(28)

式中，k1为一常数，该参数决定了反步法第1步中控制器的增益，且影响系统的最终输出。

(2)反步法第2步。令i=2，则有

e2=x2-x2,d

(29)

则有

(30)

此时令李雅普诺夫函数为

(31)

该函数的李雅普诺夫导数为

(32)

则期望值x3(此时为x3,d)应该选择的控制方式为

(33)

式中，k2的作用同k1。

(3)反步法第3步。由于阀控非对称缸的数学模型(19)和(20)中第3个方程含有众多未知或随时间缓慢变化的参数(如油液的弹性模量E、液压缸的内泄漏系数cli和阀口流量常数g)，因而，在这一步中，应该加入自适应控制策略。令i=3，则

e3=x3-x3,d

(34)

即

(35)

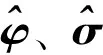
由此得到李雅普诺夫函数为

(36)

式中，Γ、η的大小决定了系统自适应调整的快慢程度。则

(37)

为了使含有φ、σ的那一项为零，要求

(38)

则式(37)变为

(39)

当

(40)

时，系统收敛。其中k3的作用同k1。

反步法第4步，设i=4，则有

e4=x4-x4,d

(41)

即

(42)

令李雅普诺夫函数为

(43)

其导数为

(44)

令

(45)

则系统收敛。同样，k4的作用同k1。

当xv<0时。其反步法的推导过程中，只有第3步有不同，但其原理是相同的，限于篇幅，本文不在赘述。需要注意的是，在控制算法的设计中，只需加入如果判别语句进行选择判断就可以了。

3 功率键合图的阀控非对称缸模型

3.1 功率键合图

为了验证仿真算法的正确性，本文采用功率键合图的方法来进行验证。其优点是模块化的结构与系统本身各部分的物理结构及各种动态影响因素之间具有直观、形象和一一对应的关系；另一方面，它与系统数学模型即状态方程之间存在着严格的逻辑上的一致性，可以有规律地推导出数学模型，得到标准形式的状态方程。特别适合进行计算机建模与仿真分析[15]。

3.2 阀控缸的功率键合图模型

为了系统模型描述的方便和模块化，将阀控缸系统的功率键合图模型拆分成伺服阀的模型和非对称缸的模型。其中伺服阀功率键合图的主体部分仿真伺服阀的4个节流边，而阀芯的动态特性用一阶惯性环节来模拟；非对称缸的模型用变换器(TF键)来模拟，内泄漏用阻性元件来模拟。在20-sim软件中所建立的阀控非对称缸的功率键合图仿真模型如图2所示。仿真过程中所采用的参数如表1所示。