基于代理模型法的叠片式吊钩热-结构应力分析
2022-03-02吴景华高崇龙
赵 杰,吴景华,高崇龙,焦 雄,王 岸
(甘肃酒钢集团宏兴钢铁股份有限公司,甘肃 嘉峪关 735100)
0 前言
起重机是垂直提升和水平搬运重物的重要机械设备[1]。冶金起重机是桥式起重机的典型类型之一,工作在冶金铸造车间,横架于车间上空,沿铺设在两侧高架上的轨道上的轨道纵向运行,用于调运熔融金属的起重设备[2,3]。冶金起重机的工作环境温度在-10 ℃~+50 ℃之间,所调运的熔融金属对锻钩、板钩的辐射温度一般最高可达300 ℃[4-5]。冶金起重机吊钩作为起吊过程直接的受力部件,在实际工作中不仅受到重力载荷的作用,而且在吊运熔融金属时由于热辐射还会产生热应力[6,7]。因此,对吊钩进行力学分析有必要考虑重力载荷和热载荷的耦合作用[8]。
目前国内针对吊钩的分析很少考虑热载荷的影响[9,10],但冶金起重机吊钩产生磨损甚至是疲劳断裂是在重力载荷和热载荷的共同作用下造成的,吊钩断裂威胁到工作人员的生命安全的问题尚未得到彻底解决[11-13],对冶金起重机吊钩进行热-结构耦合有待深入研究。另外工程中对吊钩进行疲劳寿命分析需要计算大量的热-结构耦合条件下的应力样本[14-15],而使用有限元软件进行分析会占用大量的计算资源[16-18],因此有必要采用建立代理模型[19,20]的方法来提高计算效率。
本文以工程应用广泛的叠片式起重吊钩为研究对象,根据实际工况采用有限单元法对吊钩进行了热-结构耦合仿真模拟,在给定工况温度下,模拟计算了不同重力载荷下吊钩的应力分布,获得了对应的最大应力值,建立了以重力载荷为输入,以最大应力值为输出的热-结构耦合求解的代理模型,并验证了模型应用的准确性。
1 吊钩几何模型的建立
本文参考起重吊钩的标准文件《GB/T 10051.15-2010》,以起重量63 t,钩腔直径D=320 mm的叠片式单钩为例,其主要设计参数如表1所示。

表1 起重吊钩(63 t)的设计参数
通过表1建立单个钩片的模型,省略铆钉、钩片衬垫等可拆卸零件,装配后建立其物理模型如图1所示,厚度为t=5×26 mm。

图1 63 t叠片式起重吊钩
2 有限元模型建立与模拟
将三维模型导入有限元分析软件中,设置材料的参数如表2所示,使用六面体网格对吊钩进行网格划分,得到网格单元和节点数量分别为263 900和550 706,产生的有限元网格模型如图2所示。

表2 吊钩的材料属性参数

图2 起重吊钩有限元网格模型
在吊钩实际的工作环境中,受钢包中熔融铁水的热辐射影响,其结构内部相应产生热应力,所以钢包起重吊钩的应力来自于热载荷和结构载荷两部分。
热应力是温度改变时,吊钩由于外在约束以及内部各部分之间的相互约束,使其不能完全自由胀缩而产生。吊钩中的位移约束往往存在于吊耳位置处,随着温差越来越大,吊耳处由热载荷产生的应力比重也会越来越大。在实际工况中,吊钩的底部和顶部温差相差不会太大。基于上述内容,本文设定吊钩的底部工作环境温度为200 ℃,顶部的工作环境温度为60 ℃,将吊耳作为固定约束来研究随着钢包重量的变化其内部最大应力的变化情况。
首先考虑没有热载荷的情况下,设置各个钩片之间的接触关系设置为“Bonded”,吊耳设置为固定约束,在钩腔面上施加50 kN的重力载荷,得出其应力应变云图如图3、图4所示。
设定吊钩的热边界条件分别为吊钩的底部曲面(200 ℃)和顶部曲面(60 ℃),材料的热膨胀系数是1.2×10-5℃-1,热传导系数为60.5 W·m-1℃-1,吊耳设置为固定约束,在钩腔面上施加50 kN的重力载荷,得出热-结构耦合情况下的应力应变云图如图5、图6所示。

图3 50kN载荷下吊钩的应力云图图4 50kN载荷下吊钩的应变云图图5 50kN载荷下吊钩的热力耦合应力云图图6 50kN载荷下吊钩的热力耦合应变云图
通过对比只受到重力载荷的吊钩应力应变云图和热-结构耦合状况下的应力应变云图,可见热载荷对吊钩的受力产生了显著的影响。如图3所示,吊钩其他位置的应力分布较为均匀,最大应力出现在吊钩的钩腔的截面位置处,应力较为集中且数值大小为78.83 MPa。在图5中,最大应力出现在吊耳的约束位置处,最大应力是141.26 MPa,比不考虑热载荷的情况下增加了79.5%,钩腔截面此时的应力为114.51 MPa,符合实际工作中的应力状态。
由本文分析内容可知,当引入热载荷之后,最大应力的产生位置由钩腔的截面位置处转移到了吊耳的约束位置处。这是由于在受热载荷时,约束位置处产生热膨胀时受位移约束,所以会产生相当大的热应力,但是实际工程中失效位置常为钩腔截面,所以本文仍将钩腔截面作为研究目标进行热-结构耦合应力分析。设定吊钩的底部工作环境温度为200 ℃,顶部的工作环境温度为60 ℃,在钩腔表面施加20次数值不同的载荷,获得钩腔截面的20组载重和应力的关系,如表3所示。
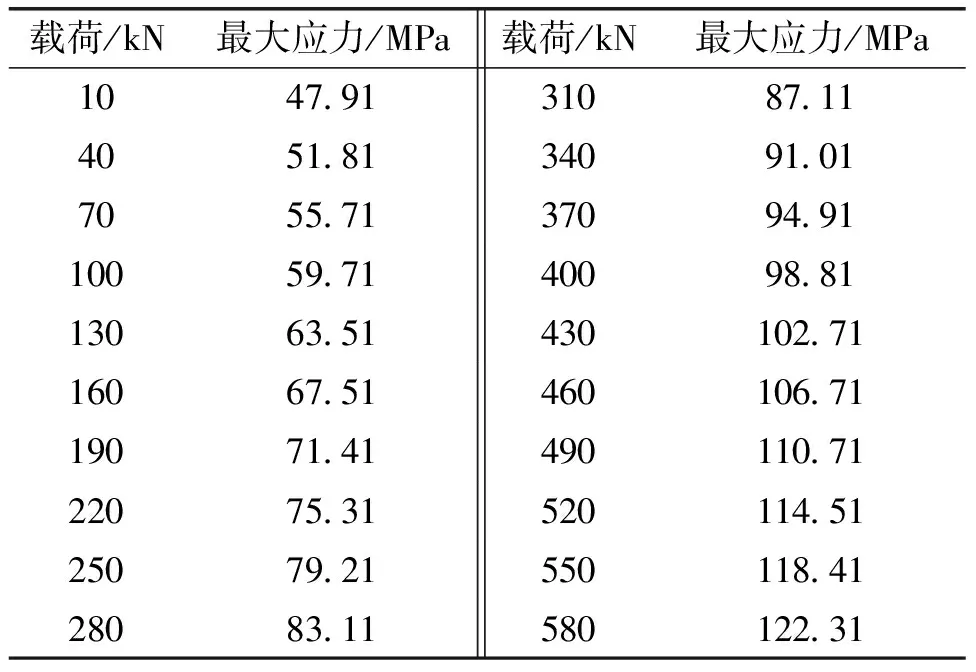
表3 20组不同重力载荷下起重吊钩钩腔截面的最大应力值
3 基于支持向量回归代理模型
在实际起重吊钩的有限元仿真过程中,每修改一次参数进行仿真计算都需要消耗大量的计算资源和时间,大范围计算吊钩应力时,传统有限元计算方式就难以实现。在这里使用支持向量回归模型来代理起重吊钩在不同载重下的最大应力计算模型,从而实现在已知载重的情况下,能快速预测出起重吊钩的最大应力数值。支持向量回归可以写成数学表达形式
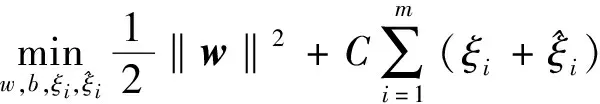
s.t.f(xi)-yi≤ε+ξi


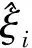
建模流程:首先通过有限元计算获得20组不同重力载荷下的最大应力值,选择表3中的15组数据,对其进行数据标准化处理,然后进行PCA降维处理,最后代入SVR训练模型中获得SVR代理模型。支持向量回归模型建立示意如图7所示。
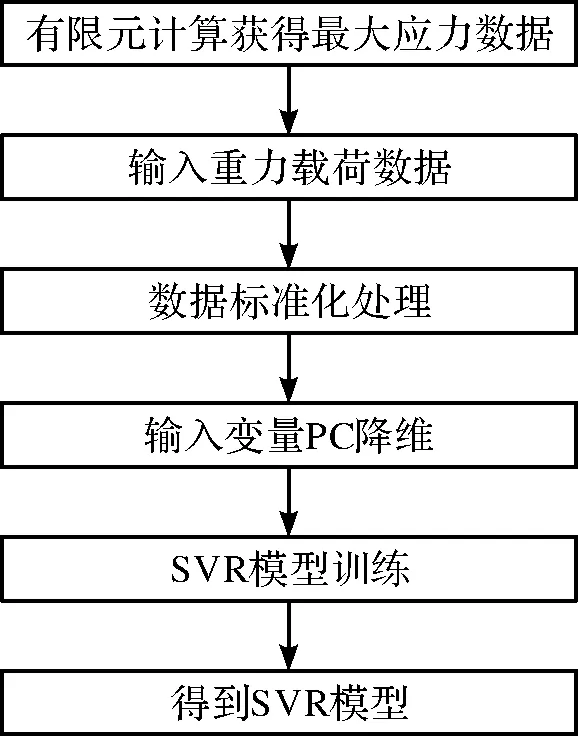
图7 支持向量回归模型建立示意图
设定吊钩的温度约束和位移约束等条件后,在钩腔表面施加20次数值不同的载荷,获得载重和应力的关系如表3所示,并将其用于代理模型的训练和验证。选择15组样本作为训练集来训练模型,获得的SVR模型,其中SVR模型中的系数为α为(-0.348 7,0.348 7),μ=22 000,获得训练模型的残差如图8所示。

图8 训练模型残差图
由图8可知,预测误差率最大不超过2%,可以接受。选择剩余的5组样本作为测试集,通过SVR模型计算出相应的最大应力值,计算结果入表4所示。

表4 有限元模型和SVR模型得出的应力结果对比
在表4中,通过代理模型求出的预测值与有限元模型获得的应力值相比误差较小,验证代理模型效果较好。同时,由代理模型求解特定重力载荷下的应力状态只需要几十秒的时间,而通过有限元模型计算则需要几十分钟甚至几个小时的计算时间,所以代理模型在需要大量应力数据时或者需要快速计算时较于传统有限元计算更便捷。
在进行机械结构设计的时候,常常需要进行结构的可靠性分析。尤其结构复杂时,应用软件对模型进行有限元分析是常用的手段之一,但是进行一次有限元分析往往需要消耗大量的时间与计算资源,有时候会严重阻碍项目的进度安排,但是建立代理模型之后,就可以对模型的一些应力应变数据进行快速的获得,方便工程师对现有结构的安全性进行判断。
4 结论
本文根据叠片式吊钩的实际工况在有限元软件中进行了热-结构耦合仿真,求出在给定工况温度下,20组不同重力载荷下对应的最大应力值,选择其中的15组重力载荷和最大应力值作为代理模型的输入参数和输出参数建立了耦合求解的代理模型,用剩余的5组重力载荷-最大应力值作为对比数据,结果表明所建立的代理模型误差较小,可以快速的计算某重力载荷对应的最大应力值。
在实际吊取钢包的过程中,吊钩承受了重力载荷和热载荷,由热载荷引起的变形虽然较小,但是在吊钩受固定位移约束时,其由热载荷引起的热应力将会变得非常大。本文分析了起重吊钩在热-结构耦合作用下的应力变化情况,建立了基于支持向量回归的代理模型来快速获得在特定载荷下对应的应力最大值,最后通过与有限元方法得出的结果作对比,同时代理模型求解特定重力载荷下的应力状态只需要几十秒的时间,而通过有限元模型计算则需要几十分钟甚至几个小时的计算时间,验证了所建模型的有效性。
