基于EEMD-FastICA的位移摄像测量误差源探究

周华飞 蒋贤辉 余忆彬 王哲

摘 要：隨着摄像测量技术在土木工程结构健康监测领域的应用逐渐增多，摄像测量技术的长期全天候工作性能受到越来越多的关注。为探究摄像测量技术的主要误差源，提出一种基于盲源分离（Blind Source Separation， BSS）的误差源分析新方法：为了构建多通道信号作为盲源分离模型的输入信号，采用集合经验模态分解法（Ensemble Empirical Mode Decomposition， EEMD）拓展观测信号通道;采用快速独立分量分析算法（Fast Independent Component Analysis， FastICA）对输入信号进行盲分离，得到FastICA分量;分析各分量与温度、光照等环境因素的相关性，探究主分量对应的误差源;利用分离算法所得的混合矩阵逆变换，计算各误差源分量的占比，确定摄像测量的主误差源。进行长期摄像测量误差源探究试验，通过盲源分离算法分析长期摄像测量误差数据，结果表明，该算法具有良好的分离效果，可有效分离提取各误差源所致位移误差分量，在长期摄像测量中，温度为主要误差源。

关键词：摄像测量;盲源分离;集合经验模态分解;误差源探究

中图分类号：TU196.4   文献标志码：A   文章编号：2096-6717（2022）03-0020-09

收稿日期：2021-05-31

基金项目：浙江省基础公益研究计划（LGF21E080010）;国家自然科学基金（51578424）

作者简介：周华飞（1978- ），男，博士，教授，主要从事结构健康监测研究，E-mail：mailtofei@zjut.edu.cn。

Received：2021-05-31

Foundation items：Zhejiang Provincial Natural Science Foundation of China （No. LGF21E080010）; National Natural Science Foundation of China （No. 51578424）

Author brief：ZHOU Huafei（1978- ）， PhD， professor， main research interest： structural health monitoring， E-mail：mailtofei@zjut.edu.cn.

Exploration of error sources of vision displacement monitoring technique by EEMD-FastICA algorithms

ZHOU Huafei， JIANG Xianhui1， YU Yibin2， WANG Zhe1

（1. School of Civil Engineering， Zhejiang University of Technology， Hangzhou 310013， P.R. China;2. Architecture and Civil Engineering， Wenzhou University， Wenzhou 325006， Zhejiang， P.R. China）

Abstract： With the increasing application of the vision measurement technique in the civil engineering structure health monitoring，more attention has been paid to the long-term all-weather performance of vision measurement.To explore the main error source of vision measurement technique，a new error source analysis method based on Blind Source Separation （BSS） is proposed： First， in order to construct the multi-channel signals as the input signals of the blind source separation model， Ensemble Empirical Mode Decomposition （EEMD） was used to expand the observation signal channels; then， Fast Independent Component Analysis （FastICA） algorithm was used to separate the input signals， to obtain the FastICA components; next，the correlation between each component and environmental factors such as temperature， light irradiation， etc.， was analyzed to explore the error source corresponding to the principal component; finally，by using the inverse transformation of the mixed matrix obtained by the separation algorithm， the proportion of the specified error source components was calculated and the main error source of the camera measurement was determined. The error data of long-term vision measurement were analyzed by blind source separation algorithm. The results show that this algorithm has good separation effect and can effectively separate and extract the displacement error components caused by each error source. In long-term vision measurement， temperature is the primary error source.

Keywords： vision measurement; blind source separation; ensemble empirical mode decomposition; error source exploration

近年来，受益于图像传感器、计算机等硬件设备性能的提升及图像处理算法的优化，摄像测量技术已經广泛运用于航空航天、国防试验、勘察勘测、交通运输等领域[1]。在土木工程领域，摄像测量技术也为结构健康监测提供了更高效便利的可能[2-4]。然而实际应用中，受温度、光照、气流等因素影响，摄像测量得到的信号通常是包含各种误差的混叠信号。为提高摄像测量技术的使用精度，有必要对其误差源进行探究。目前，关于摄像测量技术误差源的研究报道并不多见。杜文嫚等[5]同时采用摄像测量技术与加速度传感器测量固定频率的振动信号，指出振动、气流、系统噪声等因素会造成摄像测量误差。秦良忠等[6]对高层建筑动态位移进行了全天候摄像测量，分析了降雨天气下的位移实测数据，表明降雨导致摄像测量精度明显降低。Zhou等[7]研究了控温环境下摄像测量系统的性能，发现摄像测量误差具有明显的周期性变化规律，且与其所控制的室内空气温度周期性变化规律相似。由于不同误差源引起的误差相互混叠，这给逆向探究误差源及其影响程度造成诸多困难，因此，需要一种无需知晓各种误差源信息的前提下，能分离出各种误差源并量化它们影响程度的方法。

盲源分离（Blind Source Separation，BSS）无需完全了解源信号和信号混合过程，将各独立信号从混合信号中分离出来，可利用较少的约束条件获取最多的有用信息，适用于解决摄像测量误差源探究问题[8]。其中，快速独立分量分析算法（Fast Independent Component Analysis，FastICA）基于非高斯最大化原理从观测信号中分离出独立分量，是独立分量分析的一种快速算法，已成为处理盲源分离问题的主要手段[9]。此外，盲源分离技术一个至关重要的前提是观测信号个数必须大于或等于源信号个数。受实际使用条件制约，摄像测量所获取的观察信号不一定能满足这一前提。集成经验模态分解（Ensemble Empirical Mode Decomposition， EEMD）作为一种自适应信号处理方法，能将单通道时域信号分解为一系列的基本模态分量，实现信号去噪、信号维度拓展等功能[10-11]。笔者提出一种结合EEMD和FastICA的摄像测量误差源盲分离方法。

1 EEMD-FastICA盲源分离法

针对盲源分离必须满足观测信号个数大于或等于源信号数目这一约束条件，提出一种基于EEMD-FastICA的摄像测量误差源分离方法。利用EEMD分解拓展了摄像测量信号维度，成功将盲源分离技术运用到摄像测量信号的处理上。同时，FastICA算法又进一步改善了EEMD分解分量仍存在少量模态混叠的弊端。该法结合两种算法的优势可实现摄像测量各误差源所致误差的分离，有助于对位移摄像测量误差源的探究。

1.1 集成经验模态分解

经验模态分解（Empirical Mode Decomposition， EMD）是一种自适应时频数据分析方法，不同于小波分析等不具备自适应能力的信号处理方法，该方法在信号处理过程中无需人为干涉，被广泛运用于各大领域[12-13]。EMD按照一定规则将时域信号分解为一系列频率由高到低排列的基本模态分量（Intrinsic Mode Function， IMF），具体步骤是：首先，通过微分运算确定原始信号的所有局部极值点;接着，利用三次样条曲线将所有的局部极大值和极小值分别连接形成上下包络线，并由上下包络线得到均值曲线;然后，将原始信号减去均值曲线得到中间信号，若中间信号满足IMF约束条件即被认定为IMF1，

并将原始信号减去IMF1作为新的原始信号，否则，以中间信号作为新的原始信号。重复上述步骤，分解新的原始信号，直至分解完成。选择不同频率的IMF分量可以组成不同的滤波器，实现滤波功能，从而达到信号去噪、拓展信号维度等目的。然而，由于EMD对极值点的选取并不完全准确，使得极值点分布不均匀，导致求取的包络线为噪声信号的局部包络和真实信号包络的组合。因此，EMD所得的IMF通常存在模态混叠现象。为改善分离混叠问题，Wu等[14]在EMD方法基础上进行改进，提出了EEMD算法。该算法将零均值、等方差的白噪声添加到观测信号中构造新信号，即

X′j（t）=X（t）+wj（t），j=1，…，k（1）

式中：X（t）为观测信号;X′j（t）为第j个添加白噪声后的新信号;wj（t）为第j次添加的白噪声;j为添加白噪声的次数。对新信号进行EMD分解，得到l个IMF分量和分解后的剩余分量。

X′j（t）=∑li=1cji（t）+Rj（t）（2）

式中：cji（t）为第j次EMD分解得到的i个IMF分量;Rj（t）为EMD分解的剩余分量。最终将每次分解所得的相应IMF分量集合求均值，得到EEMD分解的结果。

ci（t）=1k∑kj=1cij（t）（3）

式中：ci（t）为EEMD分解的最终结果。

EEMD添加的为零均值、等方差的白噪声，集合求均值时白噪声将相互抵消，从而避免了添加白噪声对原信号造成干扰，同时又克服了单次EMD分解存在一个IMF中包含不同频率尺度的信号分量或相似频率尺度的信号分量出现在不同IMF中的模态混叠情况，最终只留下信号的真实成分。理论上，添加白噪声的次数（集成平均次数）越多则越有利于信号的完全分解。大量研究证明，当添加白噪声超过百次后，分解产生的误差已不到1%，分解结果较为精确[15-16]。因此，在算法运用上将添加200次白噪声，以满足分解需求。

1.2 盲源分离

盲源分离理论认为，观测得到的m个混合信号X=（x1，x2，…，xm）T是由n个未知独立源信号S=（s1，s2，…，sn）线性组合所得，并假设n≤m，即

X=AS（4）

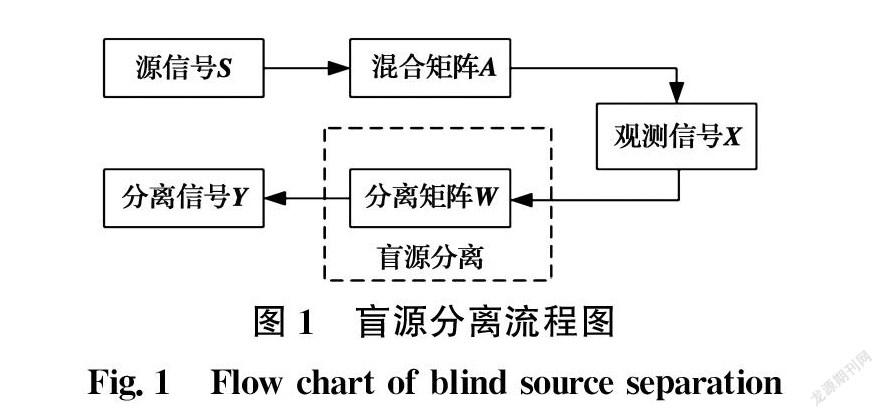
式中：A为m×n的满秩矩阵，称为混合矩阵。盲源分离流程如图1所示，其基本目标就是通过混合信号X估计出源信号S的最优逼近Y。

依据中心极限定理，多个独立源信号混合得到的观测信号较各独立源信号更趋向于高斯分布，换言之，独立源信号较混合信号非高斯性更强。FastICA算法正是基于非高斯性最大化原理，从观测信号中分离出独立分量。由信息论可知，在所有等方差的随机变量中，高斯性越强，则变量的熵越大。因此，FastICA算法利用熵的修正形式——负熵作为评价随机变量非高斯性的度量。当负熵达到最大值时，分离信号的非高斯性也达到最大，表明此时已完成各独立分量的分离，故可用负熵作为分离判别准则。相较传统的ICA算法，FastICA算法具有快速寻优迭代、计算量小、收敛速度更快、更稳健的优点，在数据处理、图像分析等领域得到广泛运用[17-18]。因此，采用基于负熵的FastICA算法进行独立量分离。

负熵可通过随机变量的微分熵来定义，对随机变量Y，其微分熵与负熵分别定义为

H（Y）=-∫f（Y）logf（Y）dy（5）

J（Y）=H（YGauss）-H（Y）（6）

式中：f（Y）是Y的概率密度函數;YGauss是与Y具有着相同方差的随机高斯变量;H（Y）是随机变量Y的微分熵;J（Y）是Y的负熵。通常情况下，f（Y）是未知的，为简化负熵的计算，可采用式（7）所示近似公式[19]。

J（Y）={E[g（Y）]-E[g（YGauss）]}2（7）

式中：E（·）是均值运算;g（·）是任意的非二次函数。g（·）的选取关系到FastICA算法的性能，目前常用的有Ye-Y22、Y3、tanh（aY）这3种函数形式，其中，采用Y3来构造目标函数时，算法的分离性能好、分离精度最高、收敛速度最快，被证明是最优的函数形式[20]。因此，选取此函数作为计算负熵的基础函数。

FastICA算法的具体流程如下：首先，对观测信号X进行去均值的中心化处理;然后，通过主成分分析对中心化后的信号进行白化处理，即利用主成分分析具有的降维功能将观测信号数目降到与源信号维数相同;接着，对上述处理后的观测信号进行线性变换，使新观测信号的各分量互不相关且具有单位方差，即

Z=MX=MAS=BS（8）

式中：Z为白化后的观测信号;M为线性变换矩阵，B为与源信号维数相同的正交矩阵，可由式（9）证明。

E{ZZT}=BE{SST}BT=BBT=I（9）

式中：I为单位矩阵。由此可见，经上述处理后，可将盲源分离估计任意全秩混合矩阵A简化为估计正交混合矩阵B。至此，即可由式（8）得到源信号

S=BTZ（10）

根据Kuhn-Tucker条件，Z的方差约束为1。对于白化数据Z而言，即将B的范数约束为1。在此条件下，使负熵最大的B可由式（11）获得。

E{Zg（BTZ）}-αB=0（11）

式中：α为常数。以F表示式（11）左边的函数，利用牛顿迭代法求解式（11），可得F的雅可比矩阵JF（B）为

JF（B）=E{ZZTg′（BTZ）}-αI（12）

式中：g′（·）为g（·）的导函数。由于Z经过白化处理，故式（12）又可进一步简化为

JF（B）=E{g′（BT）}-αI（13）

由式（11）可知α=E{BTZg（BTZ）}，带入式（13）最终得到相似牛顿迭代公式

Bi+1=E{Zg（BiTZ）}-E{g′（BiTZ）}Bi（14）

FastICA算法随机选取具有单位范数的B0作为迭代的初始矩阵，并利用式（14）迭代估算正交混合矩阵B，对迭代终值进行范数归一化即可得到最终估计值。据此，亦可得到源信号的估计为

=TZ（15）

2 误差源探究试验及初步分析

为了探究摄像测量技术的误差源，并确定其主要误差源，进行长期摄像测量试验。试验装置及布置如图2所示。数码相机采用单色1/2英寸CCD，分辨率为1 024×1 024像素，最大帧率可达60 fps。镜头为变焦镜头，焦距在25～135 mm之间。监测目标为5个被固定在一个尺寸为500 mm×500 mm目标面板上的LED灯，以便在长期连续监测中提供夜间能见度。测量系统与监测目标相距约80 m。为确定摄像测量误差，监测目标的位移真实值必须已知，然而，实际工程结构的位移真实值往往不得而知。为简化试验，采用静止的监测目标，即保持监测目标在试验全过程处于静止状态。因此，监测目标的真实位移可认为是零，而摄像测量系统得到的监测目标位移即为摄像测量过程中各误差源所致的测量误差。为提取监测目标位移，摄像测量系统从初始帧图像中提取监测目标的特征模板，并在后续帧图像中利用对象跟踪算法进行模板匹配，以初始帧监测目标的坐标为参考，即可确定监测目标的位移时间序列。试验还监测了相机温度和环境温度，受限于设备条件，试验采用外置温度传感器进行监测，其分辨率为0.1 ℃。值得一提的是，新型摄像机已经可以通过集成在内部的温度传感器来实时记录温度[21-22]，这将使得温度监测更方便。图像的采样频率为1 fps，温度的采样周期为1 min。

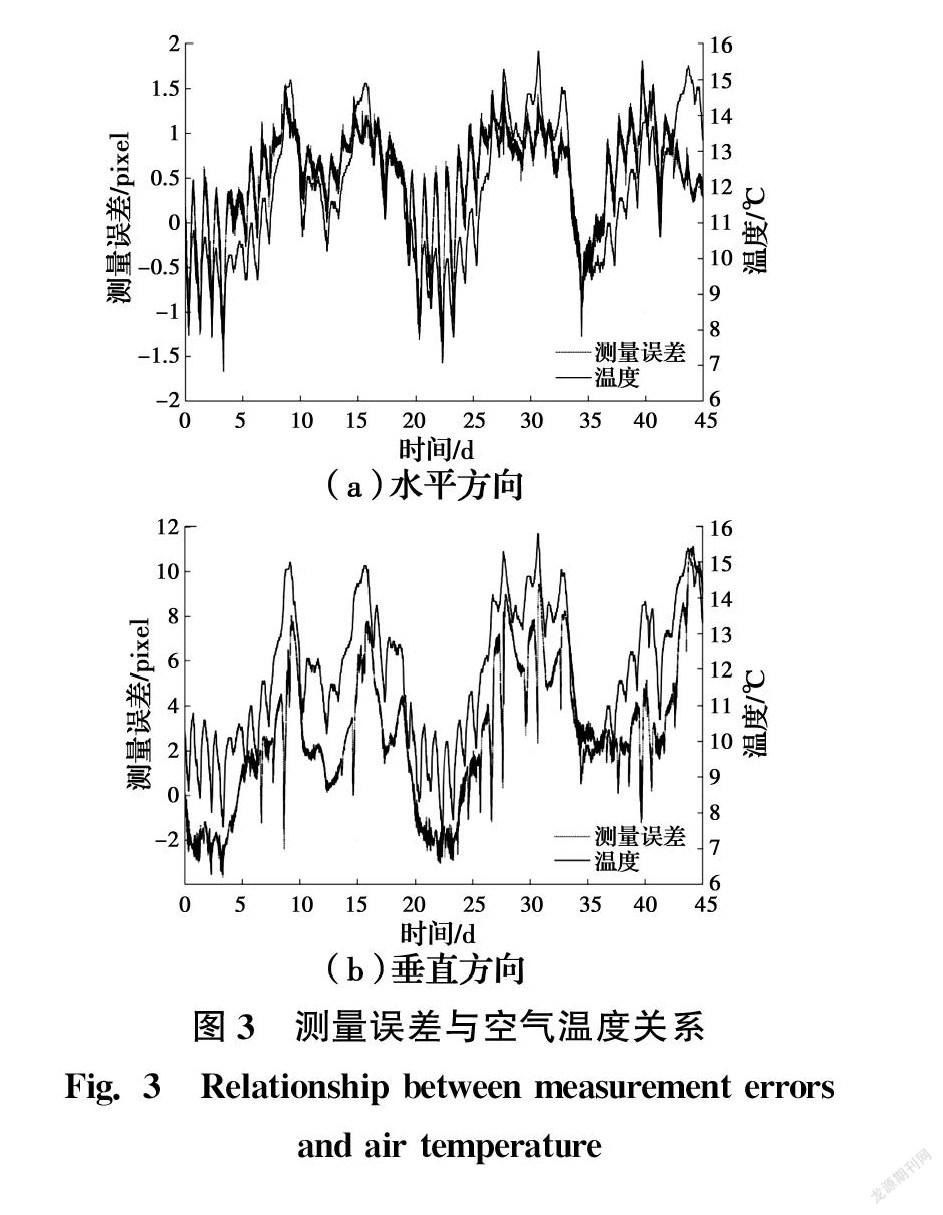
试验采集了2017年1月21日0：00到2017年3月6日23：59共1 080 h的测量数据。为消除测量数据中的随机噪声，位移测量数据采用1 min的平均值。5个测点采集到的位移数据相近，以中心目标点为例，测量误差如图3所示。可见，无论在水平还是垂直方向，都存在明显的摄像测量误差，且垂直方向的测量误差远大于水平方向的测量误差。对比空气温度数据，总体上两个方向的测量误差均与

温度表现出一定的相关性。为进一步量化测量误差与空气温度的相关性，计算了它们与空气温度的相关系数。结果表明，水平方向误差与温度的相关系数为0.593，垂直方向误差与温度的相关系数为0.515，这说明温度对摄像测量确实产生了不可忽略的影响，是摄像测量的一个误差源。然而，测量误差与温度数据的波动规律并非完全一致。

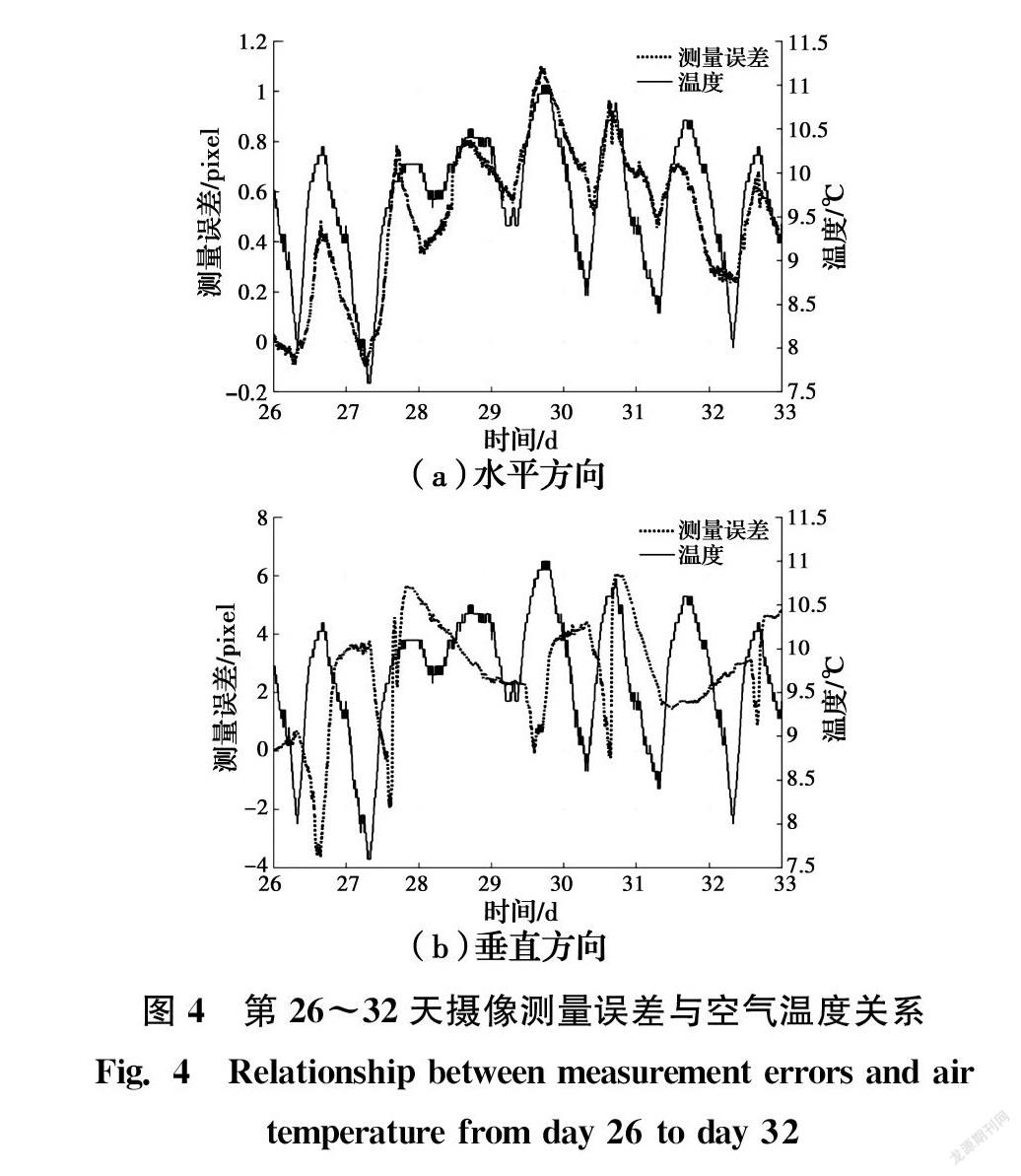
图4放大了第26～32天共10 080 min的测量误差与空气温度，由图4可见，短期内测量误差并非完全随着温度规律波动，特别是在垂直方向上，测量误差对比空气温度甚至出现了较明显的反规律现象，这表明温度似乎并非摄像测量唯一的误差源。

3 摄像测量误差分离

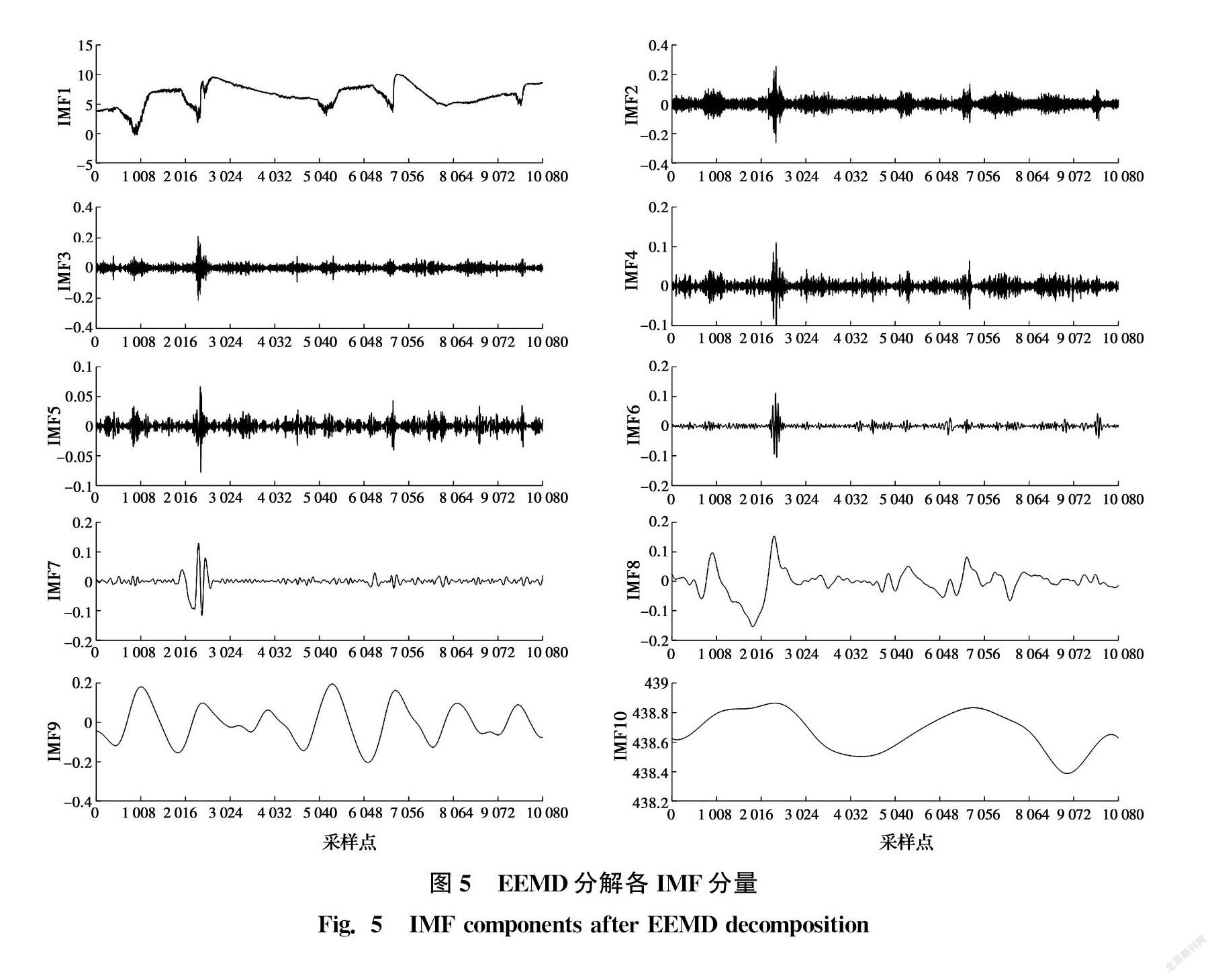
选取第26～32天的摄像测量误差数据进行盲源分离。首先，采用EEMD对摄像测量误差数据进行分解，得到一系列本征模态分量IMFs。图5为垂直方向测量误差的EEMD分解结果。由图可见，垂直向误差经EEMD分解为10个分量，其中：IMF1为原始输入信号，IMF10为分解残余分量，IMF2～IMF9是按高频到低频依次排列的各频率分量。从频率角度而言，IMF2～IMF7为短周期高频率信号，而IMF8与IMF9则为长周期低频率信号。特别地，IMF9与温度表现出相近的波动规律，故可推测其与温致误差分量相关。由于摄像测量的同一误差源可能产生不同频率的误差分量，而不同误差源也可能产生相近频率的误差分量，且由于EEMD得到的IMF仍可能存在少量的模态混叠现象，使得无法确定IMF9中是否存在不同误差源造成的同频误差分量，故不宜直接将IMF9认定为温致误差分量。其实，EEMD分解确实仍存在少量模态混叠现象，其中，IMF8即表现出了较明显的模态混叠现象，因其含有不同的时间尺度（连续峰值之间的时间宽度），如：第910 min与第2 311 min连续峰值的时间间隔为1 401 min，而第4 880 min与第5 328 min连续峰值的时间间隔为448 min，连续峰值之间的时间间隔存在较大差异，说明IMF8确实仍存在模态混叠现象。因此，利用IMF分量构建多通道信号，进一步进行FastICA盲源分离。

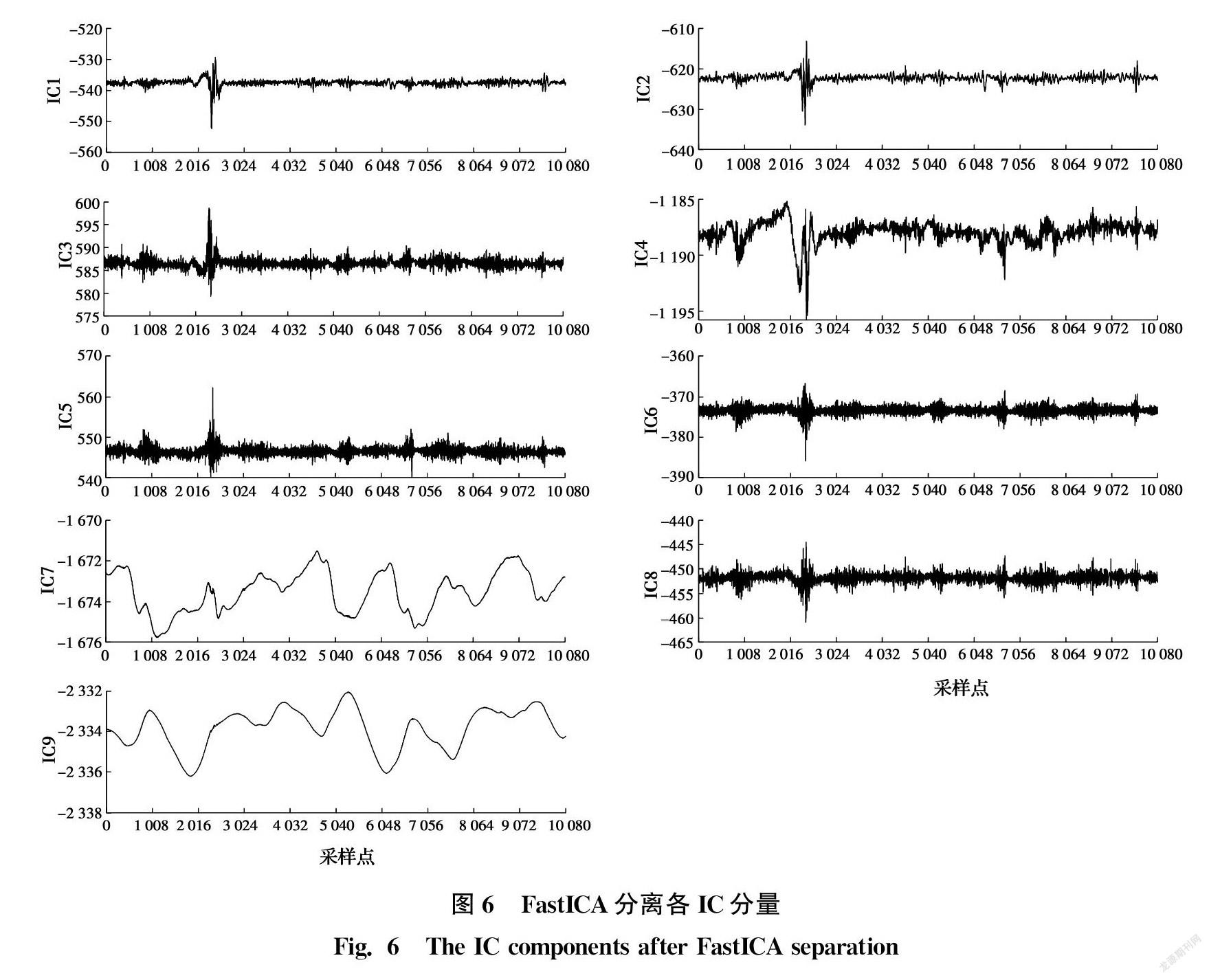
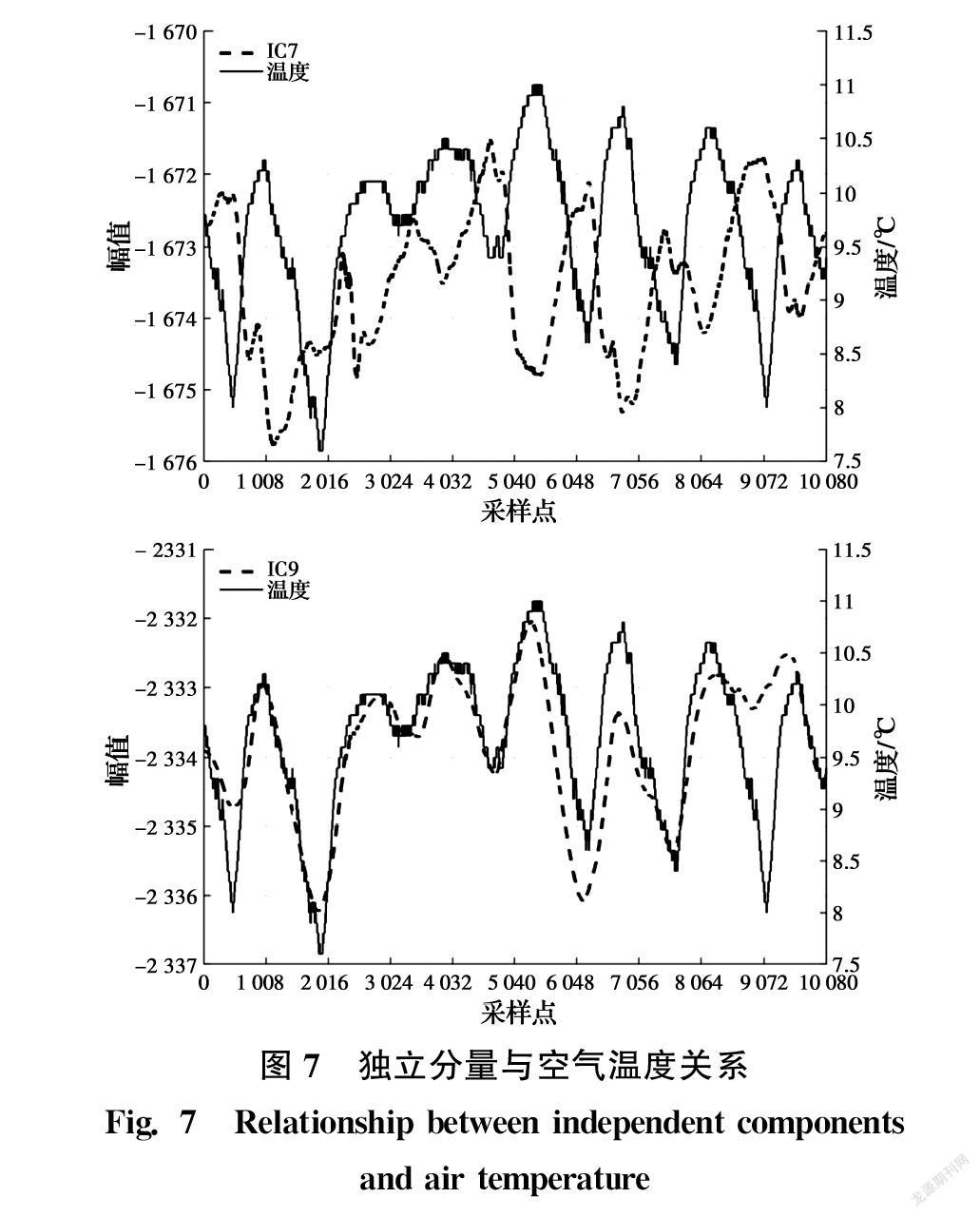
图6为利用图5所示的IMFs构建的多通道信号进行盲源分离的结果。由图6可见，IC7与IC9为长周期低频信号，而其余分量除短期内出现随机高频波动外（如IC1中，第2 016～3 024 min间出现短期大幅波动，归因于测量过程中摄像系统受到偶然因素影响），大多时段内均在较小幅值范围内随机波动，故推测这些分量均为随机噪声。就低频分量IC7与IC9而言，它们均表现出以24 h为周期的波动规律，故推测与温度有关。由于温度变化将引起摄像机机械固件的热胀冷缩，这使得图像传感器的印制电路板产生刚体位移，从而导致摄像测量产生图像漂移，即测量误差。不仅如此，由于热胀冷缩变形与温度呈线性关系，故图像传感器的刚体位移与温度可能也存在较好的线性关系，这使得图像漂移与温度之间具有较好的线性关系，从而使得两者具有较高的相关性。其实，在只考虑温度影响的情况下，已有研究表明，图像漂移确实与温度存在良好的相关性，并认为主点坐标平移是摄像测量出现图像漂移的主导原因，且主点坐标平移与温度具有良好的线性关系[7]。在多因素影响下，由于其他误差源的影响可能导致摄像测量误差与温度的相关性降低，但温度所致误差分量与温度之间仍应具有较高的相关性。因此，进一步分析它们与温度的相关性，图7给出两个分量与温度的对比情况。可见，IC9与温度波动规律具有高度一致性，两者的相关系数达0.739，故认为IC9是温度所致误差分量。然而，IC7与温度相关性较差，两者的相关系数仅为0.316，故认为IC7并非温度所致误差分量。鉴于其呈现出以24 h为周期的规律波动，初步推测其为光照所致误差分量。由于当时条件所限，试验并未记录光照数据，无法进行进一步验证。至此，可知温度是

摄像测量一个明显的误差源但并非其唯一的误差源。类似地，对水平方向误差数据进行分离处理，也可得到9个误差分量。通过各误差分量与温度之间的相关性也表明温度是摄像测量明显但并非唯一的误差源，受篇幅所限，水平向误差具体分离结果本文不再給出。

为进一步验证温致误差分量，计算了所有9个独立分量与空气温度的相关系数，结果如表1所示。由表1可见，垂直方向上，IC9与温度的相关系数为0.739，远大于其余分量;水平方向上，IC4与温度的相关系数为0.870，远大于其余分量，表明这两个分量为各自方向上的温致误差分量。值得一提的是，即使在温度未知的情况下，也可能利用先验知识大致判断出温致误差分量。如前所述，摄像测量潜在的误差源有温度、光照、气流、降雨等。一般而言，空气温度变化具有较稳定的特征，如：波动周期、升温降温模式等，这种变化规律明显区别于其他误差源。因此，可利用这些特征大致判断出温致误差分量。此外，新型的摄像机已经可以通过集成在内部的温度传感器来实时记录温度，可避免出现温度未知的情况，这将更有利于温致误差分量的推测。

对比图5与图6可知，EEMD将垂直误差数据分解为10个IMF，而FastICA利用10个IMF构建观测信号，这说明经EEMD拓展得到的观测信号数量已经足够，同时也一定程度上说明了FastICA对误差分离的完全性。此外，IC9与空气温度的相关系数为0.739，不仅高于原始数据与空气温度的相关系数0.515，也高于IMF9与空气温度的相关系数0.655，这说明FastICA改善了EEMD的模态混叠问题及可能残存白噪声的弊端，也进一步说明了FastICA对误差分离的完全性。

4 摄像测量误差源探究

上述分析确定温度是摄像测量的一个误差源，然而除温致误差分量外，也存在其他误差分量。为量化误差源对摄像测量精度的影响，确定摄像测量的主误差源，对数据做如下处理：首先，将除指定误差分量外的其余误差分量置零;然后，利用混合矩阵乘以置零后的误差分量，得到指定误差分量对应的位移误差数据;最后，计算此误差在总误差中的占比，通过占比定量说明指定误差分量对摄像测量精度的影响，确定摄像测量的主要误差源。

表2列出了垂直和水平向各误差分量对应误差占总误差的比例。垂直方向温致分量IC9对应的误差占垂直向总误差的77.12%，而其余分量对应误差占总误差最多为5.17%，次多为3.43%。类似地，水平方向温致分量IC4对应的误差占水平向总误差的84.42%，其余分量对应误差占总误差最多为3.05%，次多为2.71%。无论垂直还是水平方向，其他分量误差在总误差中的占比均远低于温致误差且基本上不超过总误差的5%。对比两个方向温致误差占比，垂直向较水平向小7.3%，也验证了前文所示，测量误差在垂直方向与温度的相关性较水平向更差的分析结果。

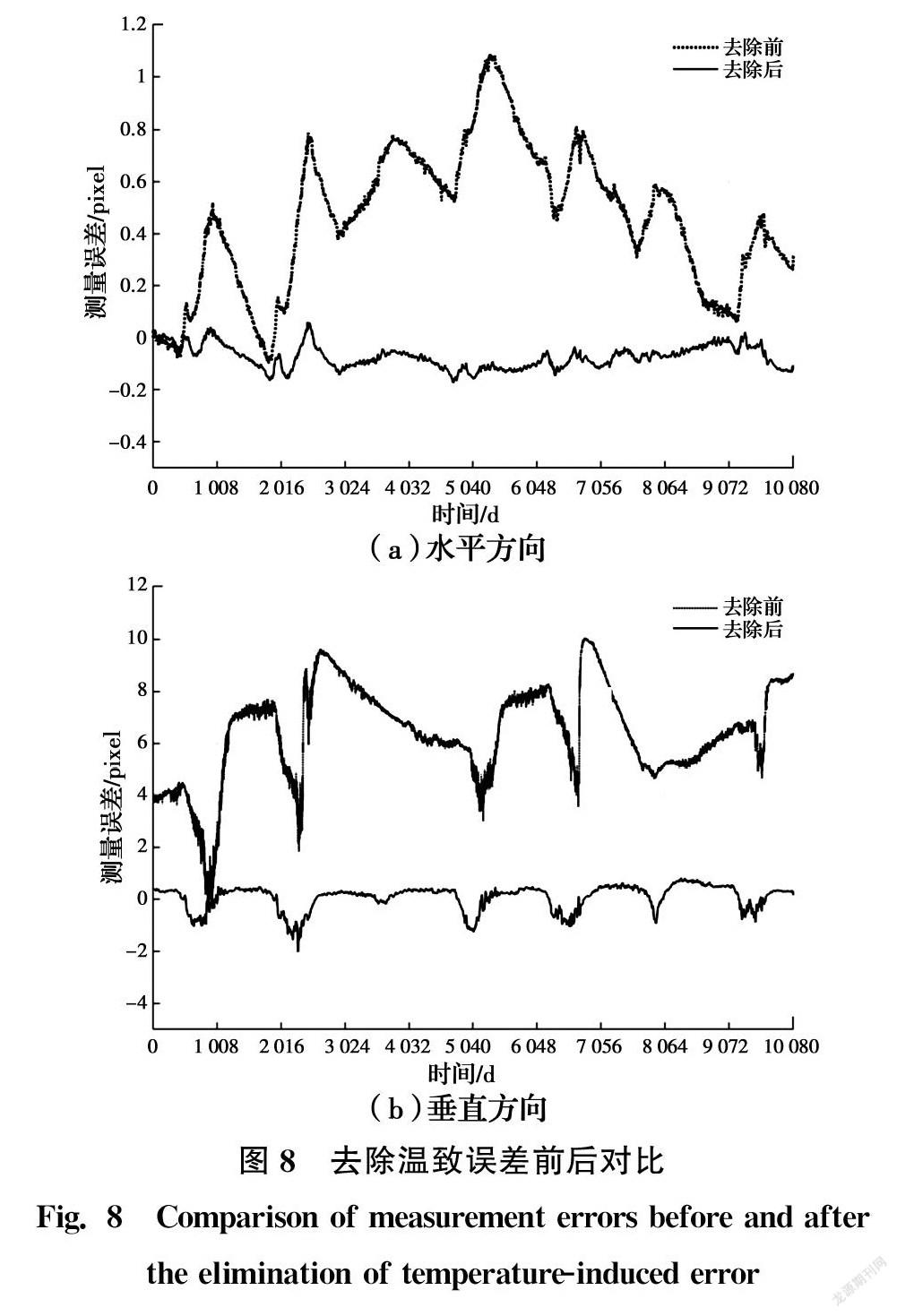
图8展示了去除温致误差前后的误差对比情况。去除温致误差后，两个方向误差均明显减小，剩余误差值在零附近上下波动。结果表明，温度不仅是长期摄像测量中一个明确的误差源也是其最主要的误差源。当然，由于试验仅同步监测了温度数据，并未监测如光照等其余可能影响摄像测量精度的误差源数据，以致误差去除并不完全，仍有少量剩余误差存在。今后可在此试验基础上增加监测光照等其他可能造成摄像测量误差的影响因素，对比各误差分量确定误差源，做到摄像测量误差的进一步去除。

5 结论

为探究长期全天候工作的摄像测量系统的误差源，提出了一种基于EEMD-FastICA的盲源分离方法，针对长期摄像测量试验实现对测量误差的分离，定量分析了摄像测量的主要误差源，主要结论如下：

1）充分利用EEMD与FastICA算法的优势，采用EEMD对摄像测量信号进行分解得到IMF分量，利用IMF分量构建多维信号，再利用FastICA对重构信号进行独立分量分析，成功将盲源分离技术运用到摄像测量信号的处理上，实现摄像测量误差的分离。

2）水平向与垂直向中均存在与温度有较高相关性的误差分离分量，水平向分量IC4与温度的相关系数达到0.870，垂直向分量IC9與温度的相关系数也达到0.739，表明温度的确是长期摄像测量中一个明确的误差源。

3）利用盲源分离所得的混合矩阵，重构各分量对应误差并计算各误差在总误差中的占比。水平向与垂直向的温致误差占总误差的84.42%与77.12%，表明温度是摄像测量明显且主要的误差源。

4）在后续摄像测量误差源研究中，可进一步探究其余误差分量各对应何种误差源，为提升摄像测量精度提供有价值的参考。参考文献：

[1] 于起峰， 尚洋. 摄像测量学简介与展望[J]. 科技导报， 2008， 26（24）： 84-88.

YU Q F， SHANG Y. Introduction and prospect of videometrics [J]. Science & Technology Review， 2008， 26（24）： 84-88. （in Chinese）

[2] XU Y， BROWNJOHN J M W. Review of machine-vision based methodologies for displacement measurement in civil structures [J]. Journal of Civil Structural Health Monitoring， 2018， 8（1）： 91-110.

[3] 尚洋， 于起峰， 关棒磊， 等. 大型结构变形监测摄像测量研究进展[J]. 实验力学， 2017， 32（5）： 593-600.

SHANG Y， YU Q F， GUAN B L， et al. Recent advances of videometrics for large-scale structure deformation monitoring [J]. Journal of Experimental Mechanics， 2017， 32（5）： 593-600. （in Chinese）

[4] FENG D M， FENG M Q. Computer vision for SHM of civil infrastructure： From dynamic response measurement to damage detection - A review [J]. Engineering Structures， 2018， 156： 105-117.

[5] 杜文嫚， 闫佳麟， 张朋波， 等. 高速摄像测量系统误差分析与研究[J]. 中国仪器仪表， 2016（1）： 43-46.

DU W M， YAN J L， ZHANG P B， et al. Error analysis and research of high speed camera measurement system [J]. China Instrumentation， 2016（1）： 43-46. （in Chinese）

[6] 秦良忠， 周华飞， 卢成原， 等. 高层建筑动态位移摄像测量环境影响及自适应滤波降噪研究[J]. 振动与冲击， 2016， 35（9）： 190-196， 218.

QIN L Z， ZHOU H F， LU C Y， et al. Environmental effects on videogrammetry for dynamic displacement monitoring of high-rise buildings and adaptive filtering for de-noising of displacement measurement data [J]. Journal of Vibration and Shock， 2016， 35（9）： 190-196， 218. （in Chinese）

[7] ZHOU H F， LU L J， LI Z Y， et al. Exploration of temperature effect on videogrammetric technique for displacement monitoring [J]. Smart Structures and Systems， 2020， 25（2）： 135-153.

[8] BELOUCHRANI A， ABED-MERAIM K， CARDOSO J F， et al. A blind source separation technique using second-order statistics [J]. IEEE Transactions on Signal Processing， 1997， 45（2）： 434-444.

[9] HYVRINEN A， OJA E. A fast fixed-point algorithm for independent component analysis [J]. Neural Computation， 1997， 9（7）： 1483-1492.

[10] HUANG N E， SHEN Z， LONG S R， et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of the Royal Society of London Series A： Mathematical， Physical and Engineering Sciences， 1998， 454（1971）： 903-995.

[11] 黎恒. 經验模态分解中的优化理论与方法研究[D]. 西安： 西安电子科技大学， 2017.

LI H. Research on the theory and approach of key issues for empirical mode decomposition [D]. Xian： Xidian University， 2017. （in Chinese）

[12] LI F， XIONG J J， LAN X H， et al. NSHV trajectory prediction algorithm based on aerodynamic acceleration EMD decomposition [J]. Journal of Systems Engineering and Electronics， 2021， 32（1）： 103-117.

[13] 鲁超， 吴贤振， 刘建伟， 等. 基于小波与EMD的井下深孔爆破振动信号对比分析[J]. 中国矿业， 2021， 30（2）： 84-90.

LU C， WU X Z， LIU J W， et al. Comparative analysis of the underground mines deep-hole blasting vibration signals based on wavelet and EMD [J]. China Mining Magazine， 2021， 30（2）： 84-90. （in Chinese）

[14] WU Z H， HUANG N E. Ensemble empirical mode decomposition： A noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis， 2009， 1（1）： 1-41.

[15] THIRUMALAISAMY M R， ANSELL P J. Fast and adaptive empirical mode decomposition for multidimensional， multivariate signals [J]. IEEE Signal Processing Letters， 2018， 25（10）： 1550-1554.

[16] 张贤达. 基于EEMD的发动机失火故障诊断[D]. 长春： 吉林大学， 2017.

ZHANG X D. Misfire fault diagnosis of engine based on EEMD [D]. Changchun： Jilin University， 2017. （in Chinese）

[17] 孟繁平. 基于改进的FastICA盲源分离算法的多人语音评测系统实现[J]. 电子技术与软件工程， 2020（20）： 124-125.

MENG F P. Implementation of multi-person speech evaluation system based on improved FastICA blind source separation [J]. Electronic Technology & Software Engineering， 2020（20）： 124-125. （in Chinese）

[18] ALDHAHAB A， MIKHAEL W B. Face recognition employing DMWT followed by FastICA [J]. Circuits， Systems， and Signal Processing， 2018， 37（5）： 2045-2073.

[19] HYVARINEN A. Fast and robust fixed-point algorithms for independent component analysis [J]. IEEE Transactions on Neural Networks， 1999， 10（3）： 626-634.

[20] 陈秀敏， 李珊君， 董兴建. Fast-ICA算法非线性函数性能的仿真分析[J]. 计算机应用与软件， 2020， 37（6）： 277-282， 333.

CHEN X M， LI S J， DONG X J. Simulation analysis of nonlinear function performance of Fast-ICA algorithm [J]. Computer Applications and Software， 2020， 37（6）： 277-282， 333. （in Chinese）

[21] ADAMCZYK M， LIBERADZKI P， SITNIK R. Temperature compensation method for digital cameras in 2D and 3D measurement applications [J]. Sensors （Basel， Switzerland）， 2018， 18（11）： 3685.

[22] DAAKIR M， ZHOU Y， PIERROT DESEILLIGNY M， et al. Improvement of photogrammetric accuracy by modeling and correcting the thermal effect on camera calibration [J]. ISPRS Journal of Photogrammetry and Remote Sensing， 2019， 148： 142-155.

（编辑 胡玲）