联合鲸鱼算法和遗传算法优化GRNN预测斜拉索覆冰厚度

汪峰 毛锦伟 刘章军

摘 要：為了预测冬季易结冰区斜拉索覆冰的增长，运用灰色关联分析方法分析斜拉索倾角、温度、湿度、风速、降雨量及气压对斜拉索覆冰厚度的关联影响，明确各影响因素的相关性大小，剔除弱相关性因素;联合遗传算法（GA）和鲸鱼算法（WOA）选择最优光滑因子，提出一种WOA-GA算法优化广义回归神经网络（GRNN）的斜拉索覆冰厚度预测方法。其特点是：以输出值与实际值均方差作为适应度函数，计算每个粒子的适应度值;将GA算法的交叉和变异算子引入WOA算法，同时借助权重更新策略，提升全局寻优的能力，避免WOA算法陷入局部最优解;最后，经过迭代寻优，输出最小适应度值对应的光滑因子，构建GRNN预测模型。结果表明：环境温度相关性最高，其次是倾角、降水量、风速、相对湿度，气压关联度最小，呈弱相关性;相比于传统的GRNN、WOA-GRNN、PSO-GA-GRNN模型，联合鲸鱼算法和遗传算法优化的GRNN覆冰预测模型精度较高，其平均绝对误差百分比仅为3.58%，均方根误差为0.58 mm;采用敏感性分析法评价影响因素对模型精度的影响，发现温度对模型影响程度最大，其次是拉索倾角。

关键词：斜拉索;覆冰预测;鲸鱼算法;遗传算法;广义回归神经网络

中图分类号：U448.27   文献标志码：A   文章编号：2096-6717（2022）03-0010-10

收稿日期：2021-03-16

基金项目：国家自然科学基金（51778343）

作者简介：汪峰（1979- ），男，博士，副教授，主要从事工程缆索结构振动控制研究，E-mail：wanggoody@126.com。

Received：2021-03-16

Foundation item：National Natural Science Foundation of China （No. 51778343）

Author brief：WANG Feng （1979- ）， PhD， associate professor， main research interest： nonlinear analysis and vibration control of cable structures， E-mail： wanggoody@126.com.

Hybrid whale optimization algorithm and genetic algorithm for optimization of GRNN for predicting stayed cable icing thickness

WANG Feng1， MAO Jinwei1， LIU Zhangjun2

（1. Hubei Key Laboratory of Disaster Prevention and Mitigation; College of Civil Engineering and Architecture， China Three Gorges University， Yichang 443002， Hubei， P. R. China; 2. School of Civil Engineering and Architecture， Wuhan Institute of Technology， Wuhan 430074， P. R. China）

Abstract： In order to estimate the icing growth characteristics of stay cables in the ice prone area in winter， the grey correlation analysis method is used to analyze the correlation effects of inclination angle， temperature， humidity， wind speed， rainfall and air pressure on the icing thickness of stay cables， and the correlation of each influential factor is determined. Then， the genetic algorithm （GA） and the whale algorithm （WOA） are combined to select the optimal smoothing factor， and a WOA-GA Optimized Generalized Regression Neural Network （GRNN） method is proposed to predict the icing thickness of stay cables. Its characteristic is to take the mean square deviation of output value and actual value as fitness function， and to calculate the fitness value of each particle; introducing the crossover and mutation operator of GA algorithm into WOA algorithm; meanwhile， via weight update strategy， the capacity of global optimization is improved， to prevent the WOA algorithm falling into local optimal; finally， through iterative optimization， the smooth factor corresponding to the minimum fitness value was output， and the GRNN pre optimization model was built. The results show that the correlation of ambient temperature is the highest， followed by dip angle， precipitation， wind speed and relative humidity， and the correlation of atmospheric pressure is the lowest; compared with the traditional GRNN， WOA-GRNN and PSO-GA-GRNN models， the proposed GRNN model has high accuracy， with the average mean absolute percentage error of 3.58% and root mean square error of 0.58 mm; The sensitivity analysis method is used to evaluate the impact of the influential factors on the accuracy of the model. It is found that the temperature has the greatest influence on the model， followed by the cable inclination.

Keywords：stayed cable; icing prediction; whale optimization algorithm; genetic algorithm; generalized regression neural network （GRNN）

斜拉桥跨越能力大、结构轻盈、造型优美，是大跨度桥梁的重要桥型。斜拉索是斜拉桥的主要承重构件，在寒冷冬季，拉索的表面容易结冰[1]，覆冰会改变拉索气动外形，诱发低频大幅的驰振[2]。当结构振动或者温度变化时，还会引发拉索冰凌坠落[3]，危害桥梁运营安全。

目前，斜拉索覆冰研究主要集中在覆冰后的气动特性，而对斜拉索早期结冰增长及预测研究相对较少。Zarnani等[4]通过支持向量机与气象资料结合的方式构建导线覆冰预测系统;Homola等[5]通过对叶片覆冰流场特性的数值研究，得到大气温度和水滴尺寸变化对风力机叶片覆冰增长过程的影响。黄新波等[6]将监测数据通过学习算法产生模糊规则，并利用模糊逻辑理论建立导线覆冰厚度预测模型;黄宵宁等[7]通过均值算法对覆冰历史数据进行优化选择，并构建LS-SVM覆冰预测模型;刘宏伟等[8]通过建立多变量灰色模型，对输电线路进行覆冰厚度预测。文献[9-11]从热力学、流体力学等角度，研究了覆冰增长机理和过程。文献[12-13]根据历史监测数据，通过对覆冰增长的相关因素进行分析，建立了数学统计模型。

近年来，随着人工智能技术的发展，神经网络方法逐步应用到覆冰预测研究领域，不同于物理模型和传统数学统计模型，神经网络针对覆冰过程的高维非线性特征具有很强的求解能力，现阶段应用较为成熟且准确度较高。赵建坤[14]采用灰色关联分析方法计算了不同影响因素对覆冰的相关性，提出了考虑微气象的BP神经网络覆冰厚度预测模型;杨静等[15]通过寻找影响覆冰局部变化的规律性，基于小波神经网络构建了短期覆冰预测模型;王锦文[16]提出了基于改进粒子群算法优化的NRBF神经网络的覆冰预测模型，提高了覆冰预测精度。Xiong等[17]在BP神经网络和支持向量机等智能预测算法的基础上提出了用思维进化算法优化结冰厚度的智能预测方法。

上述研究成果为斜拉索覆冰预测奠定了坚实的理论基础，目前，针对结构短期覆冰预测方法，主要通过神经网络建模的方式，常见的有BP神经网络和广义回归神经网络（GRNN）等，但BP神经网络中的训练参数设置烦琐，主观因素会过多影响模型的预测精度;而传统的GRNN求解过程空间复杂程度高，需要依靠大量样本。另外，其他的预测模型寻优方式单一，缺点突出，如遗传算法编程复杂，收敛速度较慢，降低了模型预测效率。笔者针对斜拉索的雨凇覆冰，运用灰色关联分析方法，首先分析斜拉索倾角、温度、湿度、风速、降雨量以及气压对斜拉索雨凇覆冰厚度的关联影响，然后联合遗传算法（GA）和鲸鱼算法（WOA）進行最优光滑因子的选择，提出一种WOA-GA算法优化广义回归神经网络（GRNN）的斜拉索覆冰厚度预测方法，并通过算例与其他预测模型进行对比验证。

1 GRNN算法优化

1.1 广义回归神经网络

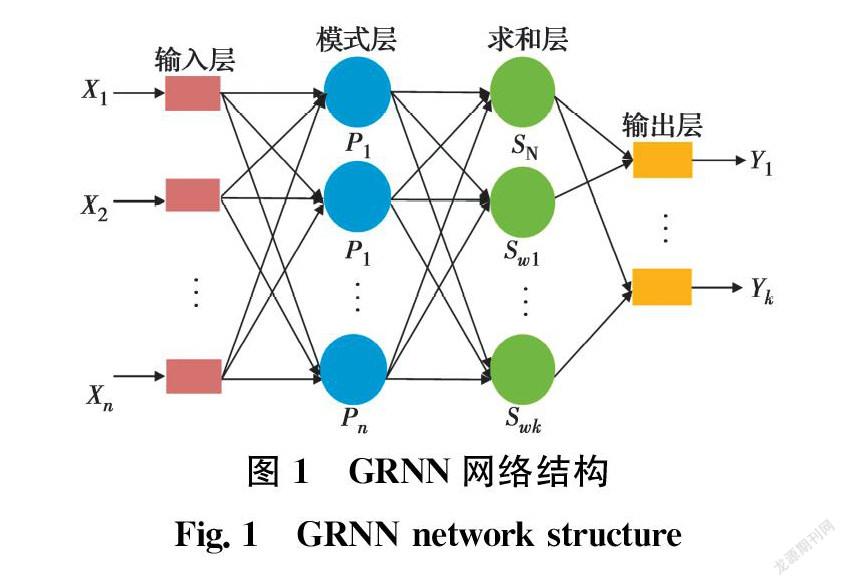
广义回归神经网络（Generalized Regression Neural Network，GRNN）具有结构简单、设置参数单一等优点[18]。在网络模型建立中仅需要调节光滑因子σ，从而最大限度地降低人为因素干扰，减少模型建立的随意性[19]。GRNN结构如图1所示[20]，包括输入层（Input Layer）、模式层（Pattern Layer）、求和层（Summing Layer）、输出层（Output Layer）。

假设随机变量x和y联合概率密度f（x，y），令x=x0，则y对于x0的回归值可表示为

（x0）=∫∞-∞yf（x0，y）dy∫∞-∞f（x0，y）（1）

训练样本的输入变量维数与神经元个数相等，根据Parzen窗非参数估计法，则概率密度函数f（x0，y）可表示为

f（x0，y）=1σp+1n（2π）p+12∑ni=1e-d（x0，xi）e-d（y，yi）（2）

d（x0，xi）=∑pj=1x0j-xijσj2（3）

d（y，yi）=（y-yi）2（4）

式中：n为训练样本的容量;p为随机变量x的维数;σ为光滑因子，也称为扩展参数。将式（2）带入式（1），整理可得

y（x0）=∑ni=1e-d（x0，xi）∫+∞-∞ye-d（y，yi）dy∑ni=1e-d（x0，xi）∫+∞-∞e-d（y，yi）dy（5）

在整体运算过程中，影响GRNN性能的关键参数为σ（光滑因子）。当σ取值过大，会使拟合结果更加趋近于样本因变量平均值，当σ取值过小，会使拟合结果接近训练样本值，减少了网络的泛化能力，降低了模型稳定性。因此，对于GRNN模型预测能力的提升，实质上转变成对光滑因子σ的寻优问题。

1.2 鲸鱼优化算法

鲸鱼算法（Whale Optimization Algorithm，WOA）基本思想来源于座头鲸狩猎行为[21]。该算法通过模拟鲸鱼特有的气泡网觅食策略来达到优化目的。以下为寻优算法的3个阶段。

1）包围猎物

由于最优问题求解并不是先验已知，鲸鱼算法会通过随机假设个体所处位置，在搜索过程中不断更新自身位置，其数学模型为

D=C→·X*（t）-X（t）（6）

X（t+1）=X*（t）-A·D（7）

式中：t为当前迭代次数;X为当前个体坐标向量;X*为当前位置最优解向量。A、C为系数向量，其公式为

A=2a·r1-a（8）

C=2·r2（9）

式中：a为收敛因子，随着迭代次数从2线性减小到0;r1和r2为[0，1]产生的随机数。

2）气泡网攻击

鲸鱼通常以气泡网攻击的方式进行捕食，为了从数学角度更好地解读这种觅食行为，设计了收缩包围机制和螺旋更新位置两种方法。

收缩包围是通过减少式（8）中的a来实现鲸鱼群体向选中个体逼近的过程，当前个体位置向量（X，Y）收缩至最优位置向量（X*，Y*）。

螺旋更新位置主要是模拟鲸鱼群体靠近猎物的路径，该方法的数字表达式是根据当前位置向量（X，Y）与当前最优位置（X*，Y*）之间的距离来确定。

3）随机搜索

除了上述气泡网攻击以外，鲸鱼会随机搜索猎物，系数A>1时，表示鲸鱼在收缩包围圈外游动，此时鲸鱼个体根据彼此位置进行随机搜索。

WOA算法随机初始化一组解，每一次迭代过程中都会根据最优解更新自身位置。在寻优过程中，收敛因子a很大程度上会影响算法的效率;过大的收敛因子虽然可以提升全局搜索的能力，但搜索速度慢;较小的收敛因子会增加局部搜索的能力，但容易陷入局部最优，导致收敛精度不高，进而无法高效地寻求最优解。

1.3 遗传算法

遗传算法是一种仿生物学算法，通过模拟自然选择来寻找最优解[22]。在遗传算法的执行过程中，利用个体对环境的适应能力决定染色体的淘汰或者保留。基本遗传算法主要由选择（Selection）、交叉（Crossover）、变异（Mutation）3种算子组成。

选择操作是指在原有群体的基础上以一定概率选择个体到新种群中，这种概率往往通过适应度值大小决定。交叉操作是指从群体中选择两个个体，通过染色体的交换来产生新的优秀个体，不同的编码方式对应不同的交叉方法。变异操作是指从群體中任选一个个体，选择染色体中的一点进行变异，从而产生更优的个体。

正是由于选择、交叉和变异等操作，才使得遗传算法具有良好的全局寻优能力，减少了陷入局部最优的可能性。但遗传算法因结构复杂，求解时间也会进一步延长，限制了局部搜索最优解的能力，从而会在接近最优解时出现停滞。

2 WOA-GA-GRNN覆冰预测模型

2.1 混合WOA-GA算法的寻优方式

目前基于GRNN的传统组合算法多采用单一寻优方式。例如GA优化GRNN[23]。由上述算法的分析可知，WOA-GRNN中的系数向量A过于依赖收敛因子a，在收敛速度和收敛精度上还需要进一步调整;同时，遗传算法求解到一定范围会出现大量无用迭代，从而导致计算时间长、效率低。因此，为解决上述两种算法的缺陷，本文考虑组合算法的模式，利用串行式[24]方法融合WOA和GA，以输出值与实际值的均方差（MSE）作为适应度函数，将GA算法的交叉和变异算子引入WOA算法中，同时，借助权重更新策略，提升算法多样性，加快收敛速度，提高收敛精度。

本文中的算法是以输出值与实际值的均方差进行方向搜索，均方差越小，说明模拟结果误差越小，因此，将均方差作为模型适应度函数值求解计算每个个体的适应度值，标记最优个体位置，其公式为

MSE=1N∑Nn=1yn-y∧n2（10）

为解决鲸鱼个体在围猎行为中的选择问题，假设在收缩包围机制和螺旋更新位置两者中选择概率均为50%，其数学模型为

X*（t+1）=

X*（t）-A·D，p<0.5

X*（t）+D·ebl·cos（2πl），p≥0.5（11）

1）交叉变异算子

遗传算法采取实数值编码，随机生成[0，1]之间的捕食行为概率值p，如果p≥0.5，则个体依据公式以变异概率Pm对该个体进行变异操作，得到新的个体。

X*（t+1）=X*+PmX*（t）-X（12）

若概率值p<0.5且A<1，进一步选择全局最优个体与当前个体进行交叉操作，获得一个新个体替换当前个体，交叉概率为Pc，其交叉公式为

Xi（t+1）=Pc×Xi（t）+（1-Pc）Xj（t）

Xj（t+1）=（1-Pc）×Xi（t）+PcXj（t） （13）

Pc为[0，1]间的随机数。Xi与Xj分别为全局最优个体与当前个体。

2）自适应权重更新策略

交叉算子虽然在一定程度上可以提升算法性能，但在局部搜索中，交叉算法结构会影响优化效率，不能很好地平衡预测模型在全局与局部之间的关系。为此，在局部搜索中参考粒子群（PSO）算法的权重更新策略[25]，当p<0.5且A≥1时，对输出值进行自适应变异更新，如式（14）所示。

X（t+1）=ωX*（t）-ACX*（t）-X（t）（14）

ω=ωmax-Gi（ωmax-ωmin）Gmax（15）

式中：ω为权重系数;Gmax为最大迭代次数;Gi为当前迭代次数。

当迭代完成后，选取最小适应度值对应的光滑因子σ，利用最优光滑因子建立GRNN模型，对测试样本进行预测。

2.2 模型构建流程与步骤

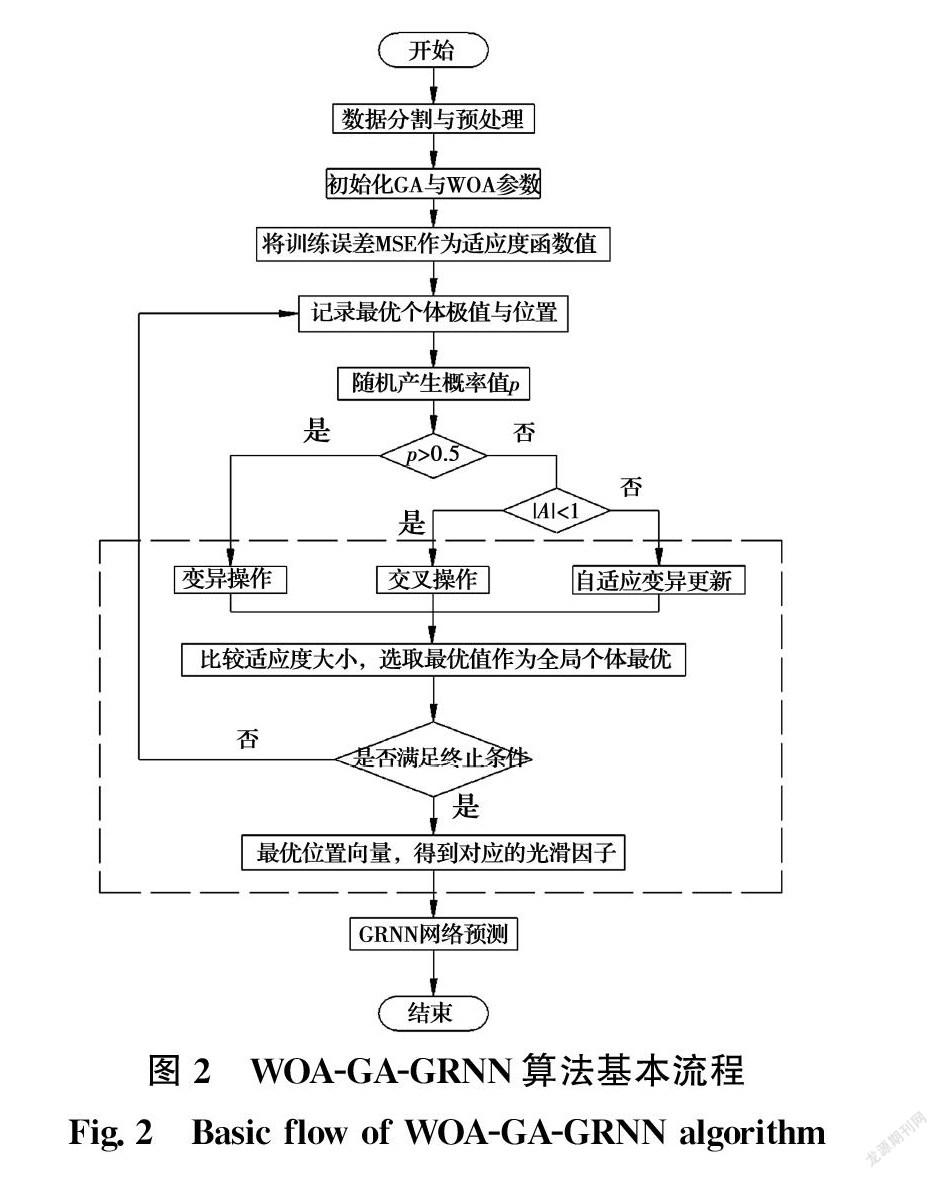
WOA-GA-GRNN建模流程如图2所示，具体建模流程如下：

1）数据分割与归一化。将数据集分成训练样本和测试样本，并将测试样本分成两组进行交叉验证，鉴于指标量纲不同，需要对试验采取的覆冰厚度、环境温度、相对湿度、风速、倾角等不同类型的数据按式（16）进行归一化处理。

xk=xk-xminxmax-xmin（16）

式中：xmin为原始数据的最小值;xmax为原始数据的最大值。

2）初始化参数设置。确定生成鲸鱼种群X，其中X是由光滑因子σ组成的一维向量，设置WOA算法以及GA算法的相关参数，如种群规模、迭代次数、变异概率、交叉概率等。

3）计算每个个体的适应度值。以GRNN网络训练样本中输出值与实际值的均方差作为适应度函数，计算每个个体的适应度值，标记最优个体位置。

4）随机生成[0，1]之间的捕食行为概率值p，判断p值大小，若p>0.5，则进行变异操作;反之，直接跳转到第5步。

5）若A<1，将全局最优个体与当前个体进行交叉操作，选择交叉后的个体替换当前个体;若A≥1，操作按照自适应函数值进行寻优替换，得到新的个体。

6）比较当前个体适应度值与历史最优适应度值大小，如果更优，则更新为全局极值，进一步与全局极值对比，选取最优值作为全局极值。

7）判断是否达到终止条件。选用最大迭代次数作为终止条件，若已达到，则停止计算。否则跳转到步骤3）。

8）选取最小适应度值对应的最优位置向量，即光滑因子σ，利用最优光滑因子建立GRNN模型，对测试样本进行预测。

2.3 模型评价指标

预测效果指标通常利用预测值和真实值之间的误差来确定，为验证模型预测效果的优劣性，选用平均绝对误差百分比（MAPE）以及均方根误差（RMSE）作为模型预测评价指标。

1）平均绝对误差百分比（Mean Absolute Percentage Error）

MAPE=100%n∑ni=1i，n-xi，nxi，n（17）

2）均方根误差（Root Mean Squared Error）

RMSE=∑Ni=1（i，n-xi，n）2N（18）

3 仿真及分析

3.1 样本选取及灰色关联性分析

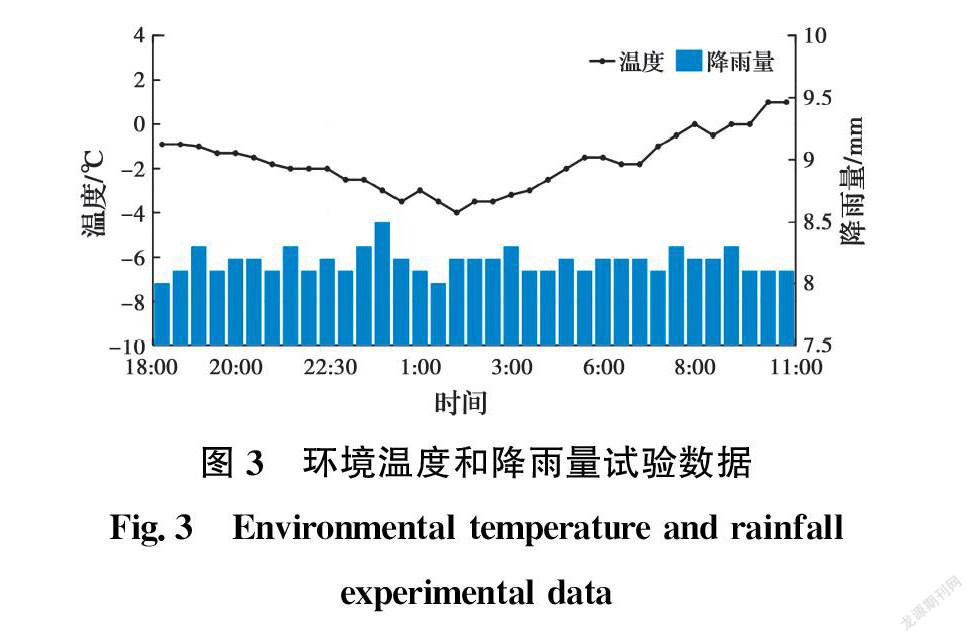
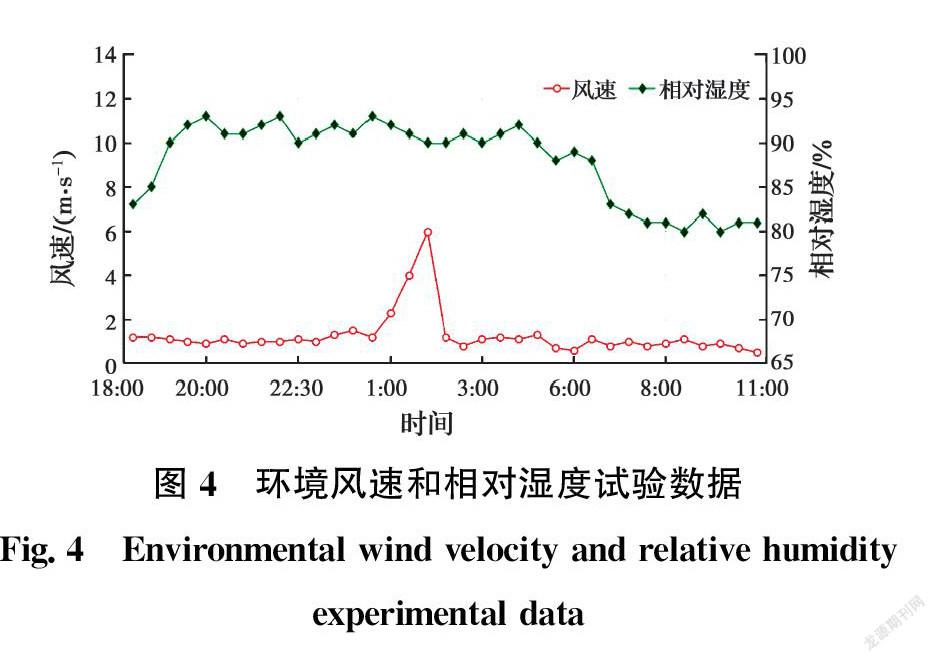
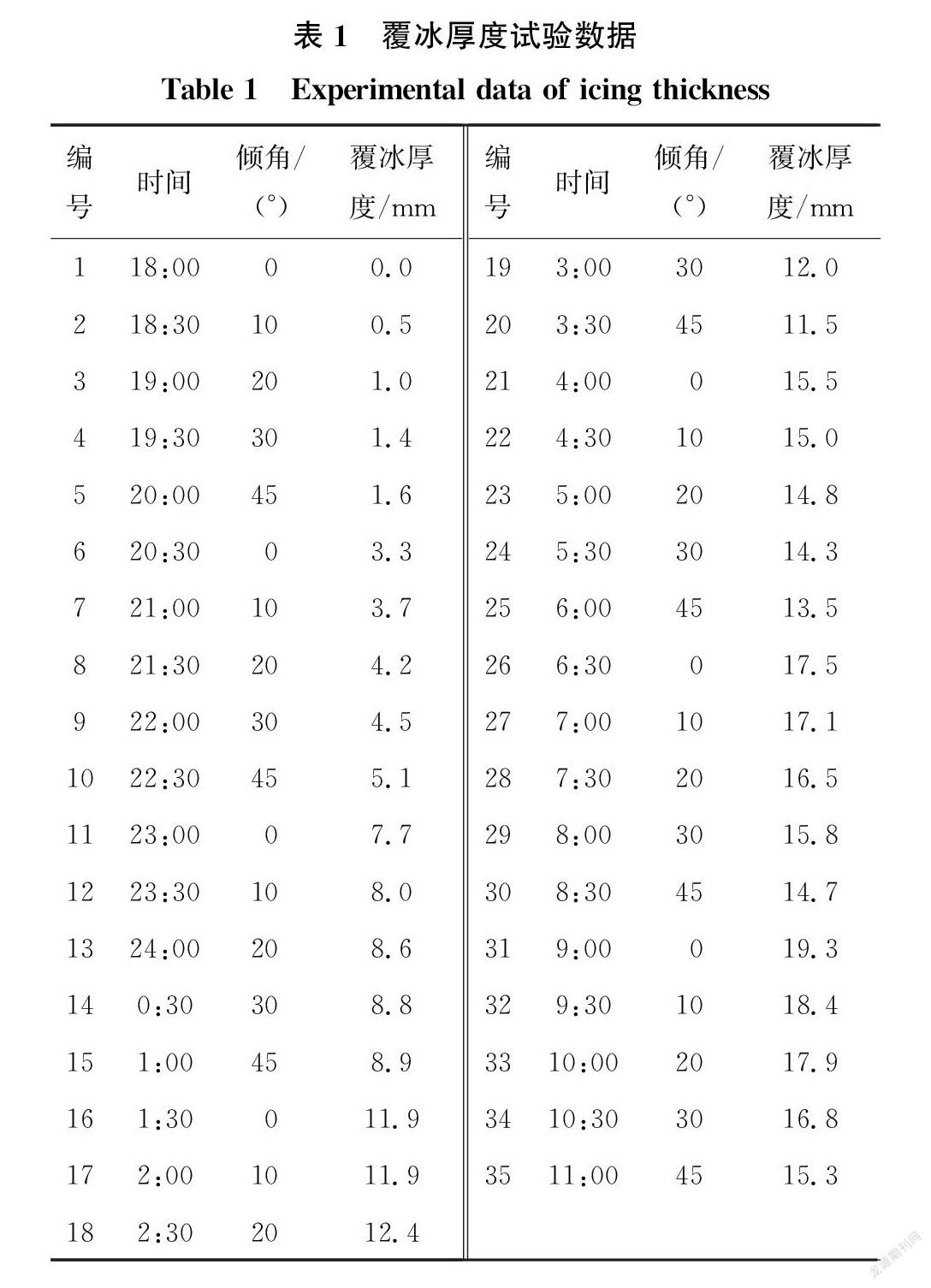
斜拉索覆冰预测较为复杂，若完全按照实际情况确定影响因素，则预测模型输入变量数较多，会导致模型学习效率降低，泛化能力減弱;若过分简化输入变量的数量，又会导致预测误差增大等问题。因此，为了准确预测拉索覆冰厚度，探索覆冰厚度增长过程与各因素间的相关关系，采用灰色关联分析，找出影响拉索覆冰厚度的重要因素，提高预测模型求解效率，提升预测效果。结合文献[26]给出的拉索覆冰试验数据，选取试验记录中18：00至第二天11：00间的环境温度、相对湿度、风速、降雨量、气压以及不同倾角下的覆冰厚度，如图3、图4所示，数据采集的时间间隔为30 min。

试验在同一环境下设置了5种倾角，分别为0°、10°、20°、30°和45°，表1记录了5种倾角下的拉索覆冰厚度，相邻两行的时间间隔为30 min。

利用MATLAB编程计算，可得到各个相关因素与覆冰厚度之间的灰色关联相关性结果，如表2所示。

一般而言，灰色综合关联度分为3类，0～0.3为无相关性，0.3～0.5为弱相关性，0.5～1为强相关性。由表2结果可知，相关性大小排序为：环境温度>倾角>降水量>风速>相对湿度>气压;其中，与覆冰厚度关联度最高的是环境温度，倾角的关联度仅次于环境温度，说明倾角是斜拉索覆冰预测的重要影响因素。风速和降水量的关联值相近，相对湿度关联度排在第5位。虽然气压与覆冰增长有所关联，但关联度处于0.3～0.5之间，属于弱相关。

3.2 预测模型的验证分析

预测模型输入变量较多时，会影响预测效率，增大预测机时。因此，为了降低变量输入维度，减小训练时间，同时，控制预测模型的计算误差，本文仅选取关联度大于0.5的强相关性因素，忽略气压的弱相关性影响，倾角、环境温度、相对湿度、风速、降雨量作为预测模型输入变量，覆冰厚度作为输出量。为了验证WOA-GA算法优化GRNN预测结果的有效性，分别采用传统单一的GRNN、WOA-GRNN、PSO-GA-GRNN对相同训练样本进行比较分析。将表1中35组样本数据分为训练样本和测试样本，其中编号1～25作为训练样本，编号26～35作为模型测试样本。

主要参数设置：种群数Size=30，最大迭代次数N=100，编码长度l=7，交叉概率PC=0.7，变异概率Pm=0.3，未经优化的GRNN在经过多次试验后光滑因子σ取值为0.1。选取输出值与实际值的均方差作为适应度函数。模型训练过程中，将训练样本划分为2组进行交叉验证。

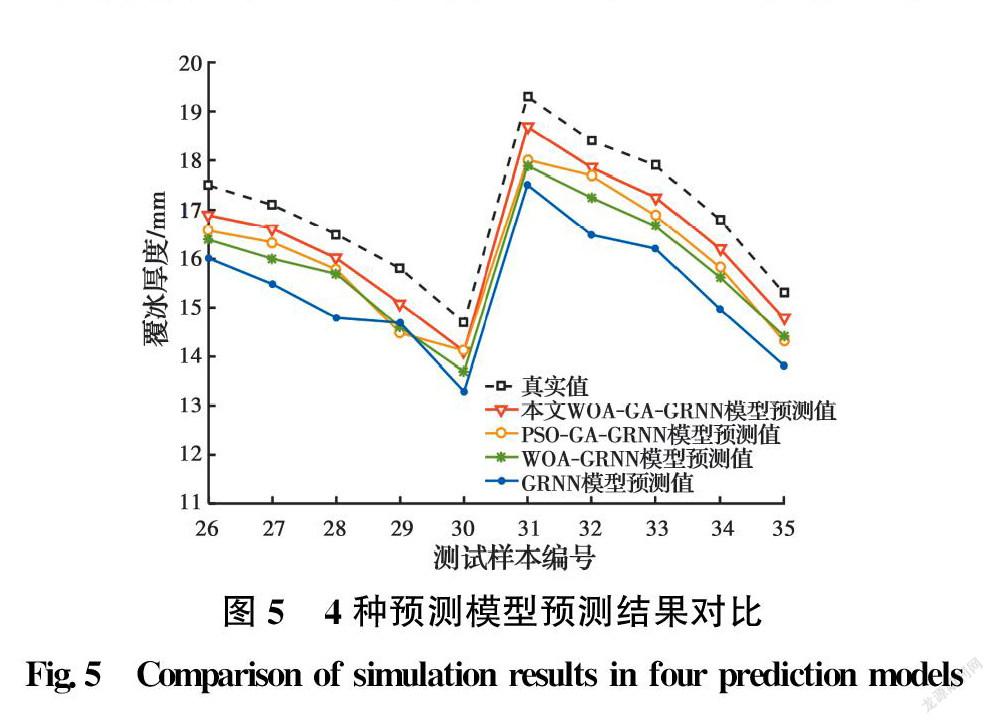
图5为4种模型覆冰预测值曲线与实际值曲线的对比。由图可知，单一GRNN神经网络和WOA-GRNN模型预测值曲线与实际值差距较大，经过PSO-GA组合优化的GRNN网络虽然较前两者有一定的提升，但由于PSO算法极易陷入到局部最优值，导致后5组预测值与实际值存在较大偏差。从图5中的预测曲线可以看出，经过鲸鱼算法和遗传算法的互补，WOA-GA-GRNN预测模型的拟合效果更符合覆冰发展的趋势，预测值也更接近实际值。

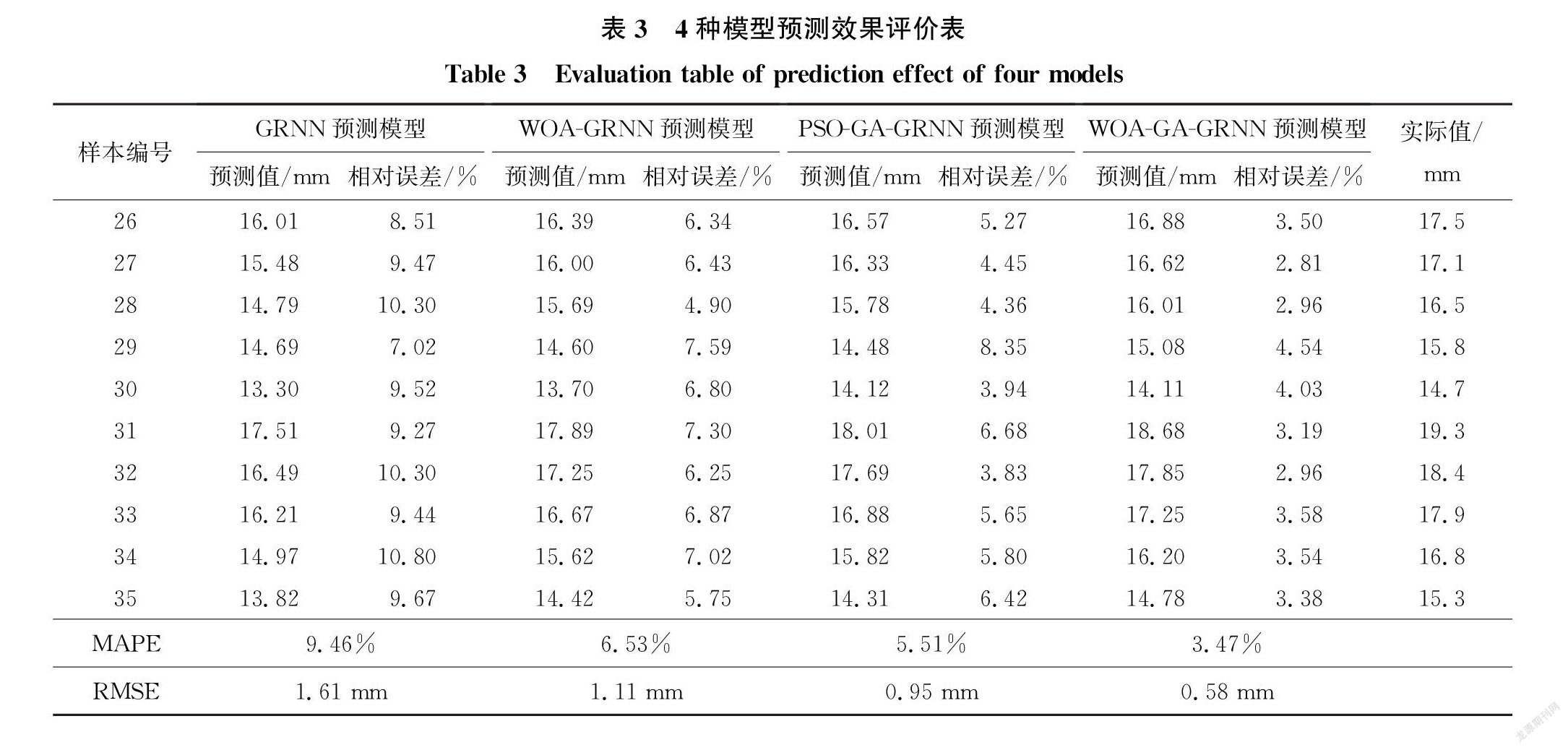
为了进一步验证模型的有效性，以平均绝对误差百分比（MAPE）和均方根误差（RMSE）作为模型精度的评价指标，得到的4种模型预测精度如表3所示。

由表3对比可知，WOA-GA-GRNN斜拉索覆冰预测模型的相对误差均在5%以下。与GRNN预测模型、WOA-GRNN模型以及PSO-GA-GRNN预测模型相比，WOA-GA-GRNN预测模型的平均绝对误差百分比较前三者分别下降了65.7%、48.9%、38.3%;与PSO-GA-GRNN预测模型相比，经过WOA-GA优化后的GRNN预测模型均方根误差下降到了0.58 mm。因此，WOA-GA混合算法优化后的GRNN网络模型可以进一步降低预测误差，模型拟合效果更优。

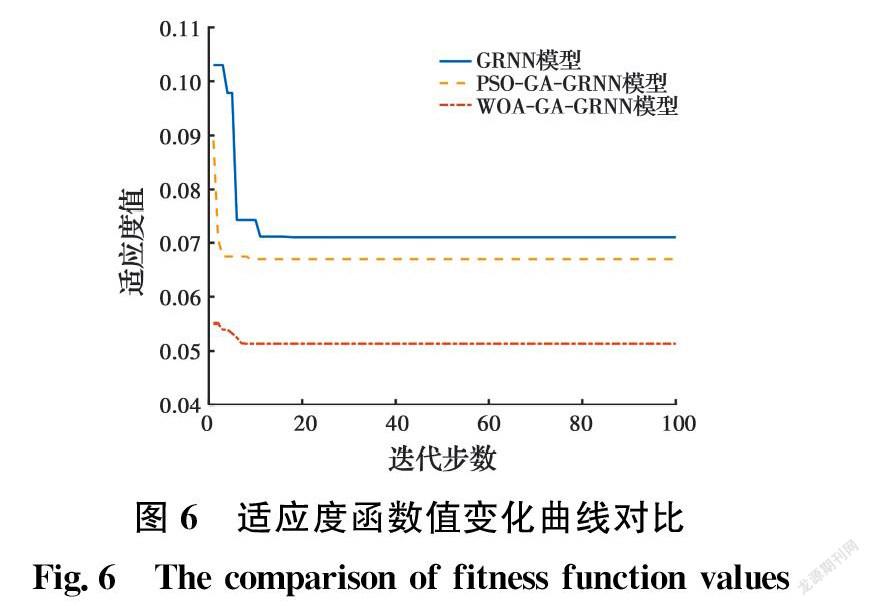
GRNN、PSO-GA-GRNN与WOA-GA-GRNN训练过程中的适应变化曲线对比如图6所示。本文算法选取训练样本中的输出值与实际值的均方差作为适应度函数，因此，适应度值越小，说明均方差越小，GRNN网络的系统误差也越小。

由图6可知，WOA-GA-GRNN模型相较于另外两种算法在收敛速度上更快。该模型将GA算法的交叉和变异算子引入WOA算法中，更新和优化个体种群，避免了WOA算法陷入局部最优解，结构简洁，运算速度大幅提升。

3.3 拟合效果分析

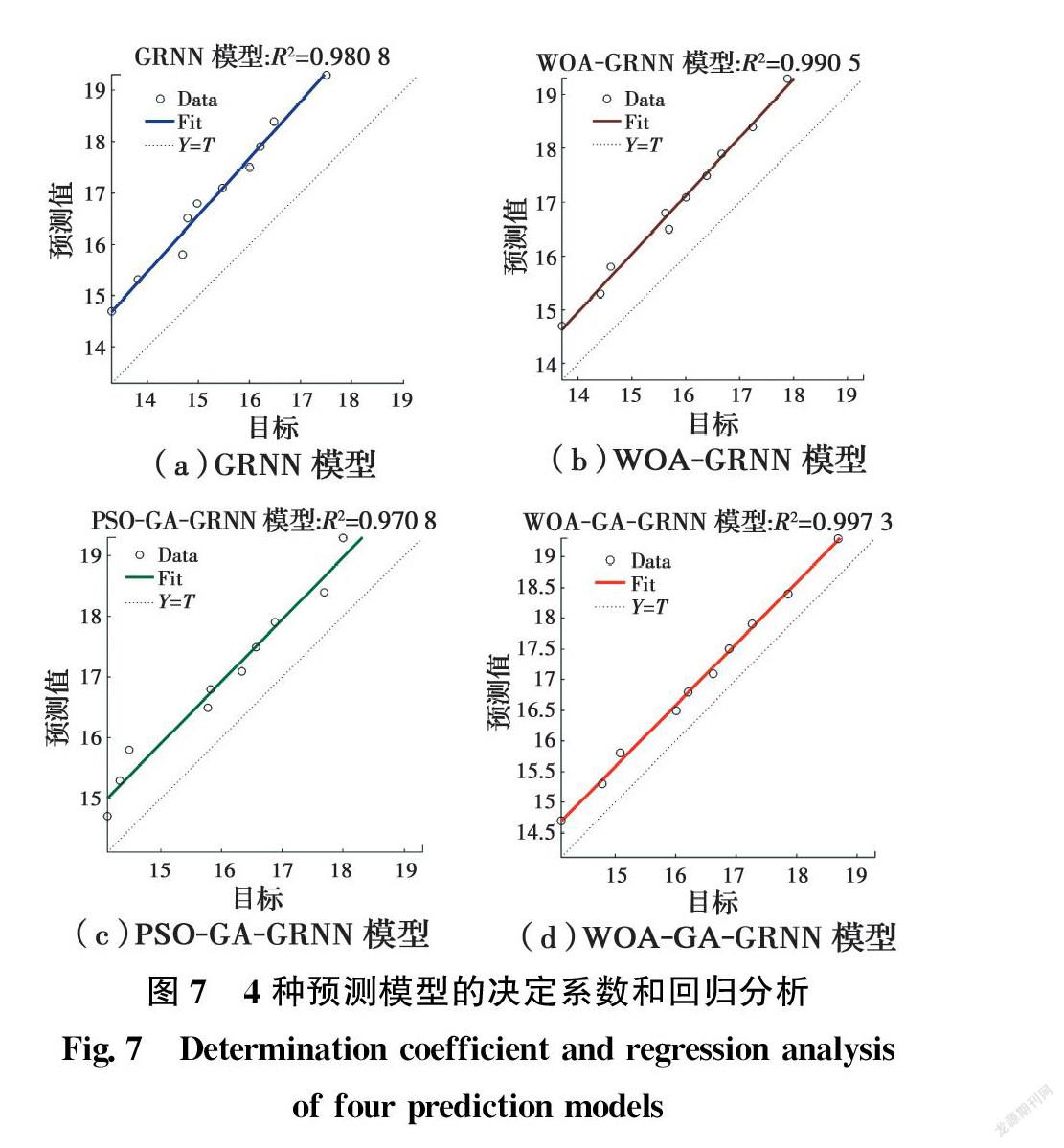
决定系数也称为拟合优度，通常用R2表示;决定系数的范围为[0，1]，R2越趋近于1，代表模型的拟合效果越好。选取决定系数作为衡量模型拟合效果的指标。4种预测模型的决定系数以及回归分析对比如图7所示。

由图7可知，WOA-GA优化后的GRNN决定系数最高。这说明模型的预测效果更加贴合实际覆冰规律。相比而言，PSO-GA-GRNN的拟合效果在4种模型中最差，但从表3中的结果来看，相对误差和均方根误差却很小。其原因是决定系数的計算类似于回归分析，是从对整个测试样本的拟合效果出发，而模型误差评价更看重单个样本与实际值的比较，决定系数注重整体，而误差分析更着眼于局部。

因此，无论从误差评价指标还是决定系数分析结果来看，经过WOA-GA优化后的GRNN预测模型更加适合斜拉索覆冰预测。

3.4 因素敏感性分析

利用因素敏感性分析方法可以直观评价出不同影响因素对模型预测精度的敏感程度。

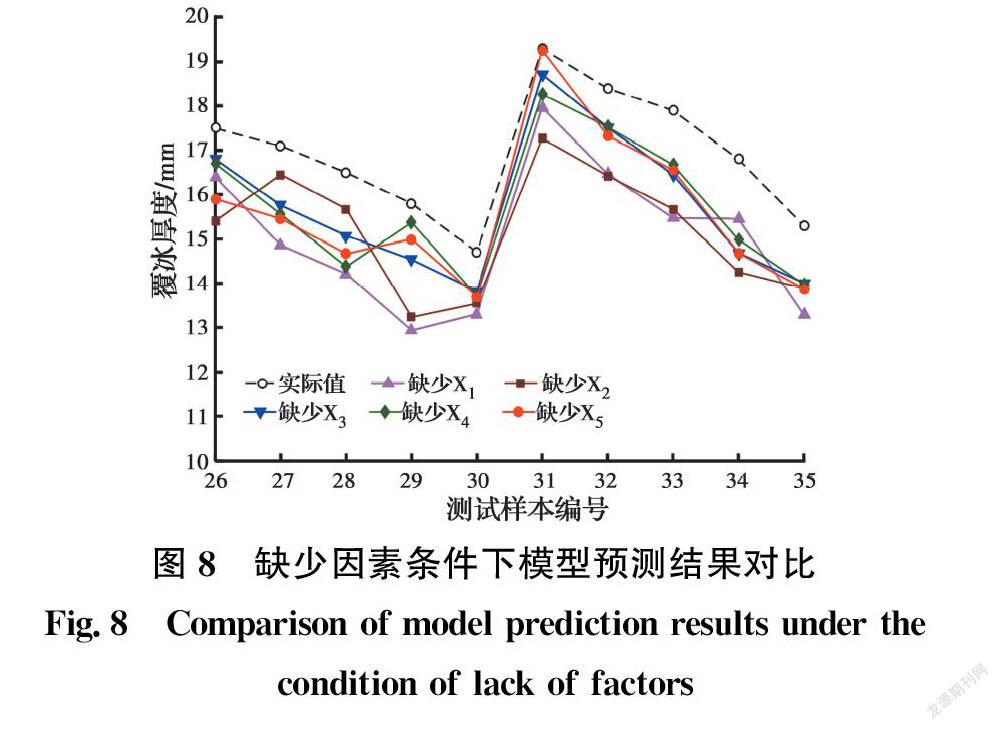
通过敏感性分析法，对5个主要影响因素分别建立预测模型，具体过程为：在其他因素均不发生变化的情况下，逐次减少单个因素Xi，建立对应的预测模型Wi。其中，i为每次减少的主要因素，与之对应的为温度（X1）、倾角（X2）、相对湿度（X3）、风速（X4）、降雨量（X5），将每一组模型预测值与实际覆冰厚度进行比较，具体预测结果如图8所示。

由图8可知，在缺少任何一种因素下的预测曲线与实际值曲线有着一定的偏差，每个样本点与实际值之间的误差较大。

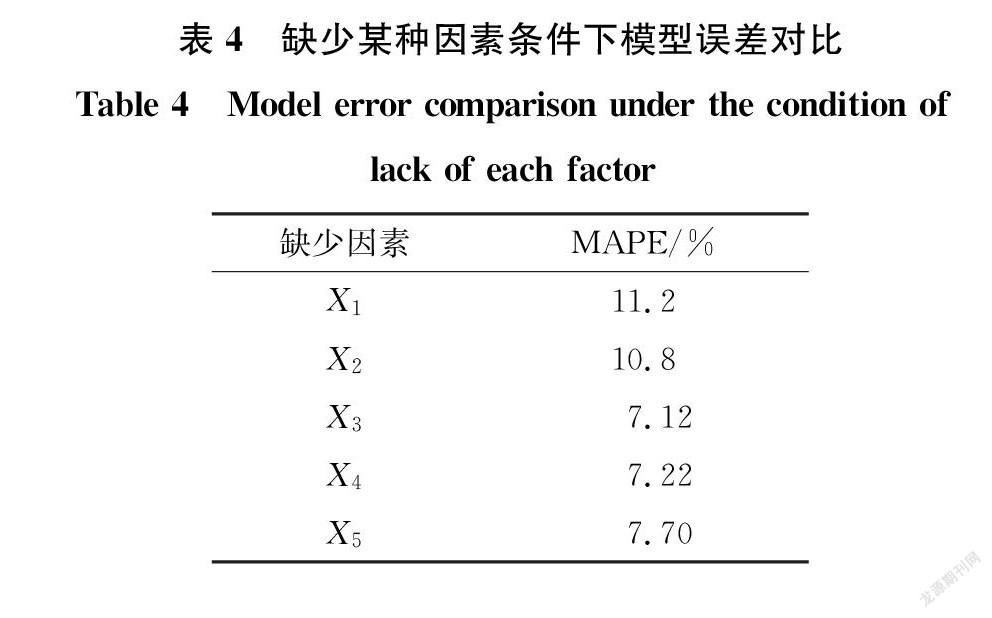
为进一步评价因素的敏感性大小，将平均绝对误差百分比（MAPE）作为敏感程度的评价指标。计算得到缺少某种因素条件下模型误差模型预测精度如表4所示。

由表4可知，斜拉索的覆冰厚度对温度（X1）最为敏感，缺少温度条件后的预测值与实际值平均相对误差为11.2%，其次为倾角（X2），缺少倾角后的平均相对误差为10.8%，敏感程度最低的是相对湿度（X3），其平均相对误差为7.12%，在缺少风速（X4）、降雨量（X5）条件下对应的平均相对误差分别为7.22%和7.10%。

实际上，影响斜拉索覆冰增长的因素较多，其中，温度是影响覆冰最基本的条件之一，在拉索表面易覆冰时的温度一般为-5～-1 ℃。如果温度过高，空气中液态水在碰撞拉索表面后因不能迅速冻结而滴落;如果温度过低，液态水与空气的热交换速率加快，水滴在下落的过程中就已经变成雪花，无法形成覆冰。

斜拉索覆冰本质上是一种能量转化的物理过程，当空气中的过冷却液滴碰撞到斜拉索上，与拉索表面形成热量交换进而固化积冰[27]。因此，在覆冰过程中，过冷却水与拉索表面的碰撞和冻结过程密不可分。另外，倾角会影响到液态水滴碰撞拉索的概率以及液滴的黏附。当空气中的液态水碰撞到拉索后，因为环境条件的影响，液态水滴并不会立刻结冰，而会随着倾斜的拉索形成滚动的水滴，倾角越大，其液态水滴的势能越大，增加了单位时间内滚动雨滴的数量，从而导致覆冰厚度随着倾角的增加而减小。

4 结论

提出了一种基于WOA-GA混合算法优化广义回归神经网络（GRNN）的斜拉索覆冰厚度预测方法，并与传统的预测模型进行对比分析，得到以下主要结论：

1）倾角、温度、相对湿度、风速、降水量与斜拉索的覆冰厚度具有较高的关联性，其中，环境温度关联性最高，依次是倾角、降水量、风速、相对湿度。气压灰色关联度低于0.5，与覆冰厚度呈低相关性，在模型输入变量选取时应当剔除。

2）WOA-GA-GRNN覆冰预测的精度高，误差小，决定系数较高。其平均绝对误差百分比仅为3.58%，均方根误差为0.58 mm，平均绝对误差百分比较GRNN、WOA-GRNN、PSO-GA-GRNN预测模型分别下降了65.7%、48.9%、38.3%。

3）敏感性大小排序为：温度>倾角>降雨量>风速>湿度。缺少倾角条件后的预测值与实际值平均绝对误差百分比高达10.8%。因此，拉索覆冰预测时，倾角不容忽视。

WOA-GA-GRNN建模方法通过在WOA中引入遗传算法的交叉和变异操作，应用混合后的算法寻找GRNN网络光滑因子最优值，克服了GRNN网络光滑因子难以确定的缺点，同时，有效改善了GA算法收敛速度慢和WOA算法粒子收敛精度不高，容易陷入局部最优等缺陷。该方法可用于斜拉索冬季覆冰短期预测。参考文献：

[1] 王凯丽， 谭冬梅， 瞿伟廉， 等. 两种典型覆冰斜拉索气动特性及驰振分析[J]. 噪声与振动控制， 2017， 37（4）： 126-131， 149.

WANG K L， TAN D M， QU W L， et al. Analysis of aerodynamic characteristics and galloping performance for two typical iced stay cables [J]. Noise and Vibration Control， 2017， 37（4）： 126-131， 149. （in Chinese）

[2] 李寿英， 黄韬， 叶继红. 覆冰斜拉索驰振稳定性的理论研究[J]. 振动与冲击， 2013， 32（1）： 122-127.

LI S Y， HUANG T， YE J H. Theoretical analysis of galloping stability for stay cables with iced accretions [J]. Journal of Vibration and Shock， 2013， 32（1）： 122-127. （in Chinese）

[3] MATEJICKA L， GEORGAKIS C T， SCHWARZ A， et al. Cable surface for the reduction of risk associated with bridge cable ice accretions [J]. Structural Engineering International， 2019， 29（3）： 425-432.

[4] ZARNANI A， MUSILEK P， SHI X Y， et al. Learning to predict ice accretion on electric power lines [J]. Engineering Applications of Artificial Intelligence， 2012， 25（3）： 609-617.

[5] HOMOLA M C， VIRK M S， WALLENIUS T， et al. Effect of atmospheric temperature and droplet size variation on ice accretion of wind turbine blades [J]. Journal of Wind Engineering and Industrial Aerodynamics， 2010， 98（12）： 724-729.

[6] 黄新波， 李佳杰， 欧阳丽莎， 等. 采用模糊逻辑理论的覆冰厚度预测模型[J]. 高电压技术， 2011， 37（5）： 1245-1252.

HUANG X B， LI J J， OUYANG L S， et al. Icing thickness prediction model using fuzzy logic theory [J]. High Voltage Engineering， 2011， 37（5）： 1245-1252. （in Chinese）

[7] 黄宵宁， 许家浩， 杨成顺， 等. 基于数据驱动算法和LS-SVM的输电线路覆冰预测[J]. 电力系统自动化， 2014， 38（15）： 81-86.

HUANG X N， XU J H， YANG C S， et al. Transmission line icing prediction based on data driven algorithm and LS-SVM [J]. Automation of Electric Power Systems， 2014， 38（15）： 81-86. （in Chinese）

[8] 劉宏伟， 陆佳政， 赖旬阳， 等. 输电线路覆冰厚度短期多变量灰色预测模型研究[J]. 高电压技术， 2015， 41（10）： 3372-3377.

LIU H W， LU J Z， LAI X Y， et al. Short-term multi-variable grey model in predicting icing thickness on transmission lines [J]. High Voltage Engineering， 2015， 41（10）： 3372-3377. （in Chinese）

[9] MAKKONEN L. Models for the growth of rime， glaze， icicles and wet snow on structures [J]. Philosophical Transactions of the Royal Society of London Series A： Mathematical， Physical and Engineering Sciences， 2000， 358（1776）： 2913-2939.

[10] 孙才新， 蒋兴良， 熊启新， 等. 导线覆冰及其干湿增长临界条件分析[J]. 中国电机工程学报， 2003， 23（3）： 141-145.

SUN C X， JIANG X L， XIONG Q X， et al. Analysis of critical icing conditions of conductor and wet-dry growth [J]. Proceedings of the CSEE， 2003， 23（3）： 141-145. （in Chinese）

[11] 蒋兴良， 申强. 环境参数对导线覆冰厚度影响的试验分析[J]. 高电压技术， 2010， 36（5）： 1096-1100.

JIANG X L， SHEN Q. Experimental research on influence of environmental parameters on the conductor icing thickness [J]. High Voltage Engineering， 2010， 36（5）： 1096-1100. （in Chinese）

[12] 江志红， 刘冬， 刘渝，等. 导线覆冰极值的概率分布模拟及其应用试验[J]. 大气科学学报， 2010， 33（4）： 385-394.

JIANG Z H， LIU D， LIU Y， et al. Study on the probability distribution simulation of conductor icing and its application test [J]. Transactions of Atmospheric Sciences， 2010， 33（4）： 385-394. （in Chinese）

[13] 邹明华， 邓洪洲. 输电线路设计覆冰厚度统计模型取用[J]. 电网与清洁能源， 2010， 26（1）： 40-44.

ZOU M H， DENG H Z. Study on probability distribution model of designed ice load for transmission lines [J]. Power System and Clean Energy， 2010， 26（1）： 40-44. （in Chinese）

[14] 赵建坤. 架空输电线路覆冰厚度预测模型研究[D]. 北京： 华北电力大学， 2016.

ZHAO J K. Research on icing thickness prediction model of overhead transmission lines [D]. Beijing： North China Electric Power University， 2016. （in Chinese）

[15] 杨静， 李英娜， 赵振刚， 等. 基于相空间重构小波神经网络的短期覆冰预测[J]. 传感器与微系统， 2019， 38（9）： 108-111.

YANG J， LI Y N， ZHAO Z G， et al. Short-term icing forecasting based on phase space reconstruction wavelet neural network [J]. Transducer and Microsystem Technologies， 2019， 38（9）： 108-111. （in Chinese）

[16] 王錦文. 基于改进粒子算法优化NRBF神经网络的覆冰厚度预测模型[J]. 电力科学与技术学报， 2012， 27（4）： 76-80.

WANG J W. Ice thickness prediction model of transmission line based on improved particle swarm algorithm to optimize NRBF neural network [J]. Journal of Electric Power Science and Technology， 2012， 27（4）： 76-80. （in Chinese）

[17] XIONG W， YUAN H J， YOU L. Prediction method of icing thickness of transmission line based on MEAO [J]. Cluster Computing， 2018， 21（1）： 845-853.

[18] SPECHT D F. A general regression neural network [J]. IEEE Transactions on Neural Networks， 1991， 2（6）： 568-576.

[19] 贾义鹏， 吕庆， 尚岳全. 基于粒子群算法和广义回归神经网络的岩爆预测[J]. 岩石力学与工程学报， 2013， 32（2）： 343-348.

JIA Y P， LV Q， SHANG Y Q. Rockburst prediction using particle swarm optimization algorithm and general regression neural network [J]. Chinese Journal of Rock Mechanics and Engineering， 2013， 32（2）： 343-348. （in Chinese）

[20] 王文辉， 骆正山， 张新生. 基于PSO-GRNN模型的埋地管道腐蚀剩余寿命预测[J]. 表面技术， 2019， 48（10）： 267-275， 284.

WANG W H， LUO Z S， ZHANG X S. Prediction on remaining service life of buried pipeline after corrosion based on PSO-GRNN model [J]. Surface Technology， 2019， 48（10）： 267-275， 284. （in Chinese）

[21] 李西兴， 杨道明， 李鑫， 等. 基于混合遗传鲸鱼优化算法的柔性作业车间自动导引车融合调度方法[J]. 中国机械工程， 2021， 32（8）： 938-950， 986.

LI X X， YANG D M， LI X， et al. Flexible job shop AGV fusion scheduling method based on HGWOA [J]. China Mechanical Engineering， 2021， 32（8）： 938-950， 986. （in Chinese）

[22] 丁杨， 周双喜， 董晶亮， 等. 人工智能方法在土木工程监测中的运用[J]. 材料导报， 2019， 33（Sup1）： 274-277.

DING Y， ZHOU S X， DONG J L， et al. Application comparison of artificial intelligence method in civil engineering monitoring [J]. Materials Reports， 2019， 33（Sup1）： 274-277. （in Chinese）

[23] 王雨， 刘国彬， 屠传豹. 基于遗传GRNN在深基坑地连墙测斜预测中的研究[J]. 岩土工程学报， 2012， 34（Sup1）： 167-171.

WANG Y， LIU G B， TU C B. Deformation prediction for deep excavations based on genetic algorithms-GRNN [J]. Chinese Journal of Geotechnical Engineering， 2012， 34（Sup1）： 167-171. （in Chinese）

[24] ROBINSON J， SINTON S， RAHMAT-SAMII Y. Particle swarm， genetic algorithm， and their hybrids： Optimization of a profiled corrugated horn antenna [C]//IEEE Antennas and Propagation Society International Symposium （IEEE Cat. No.02CH37313）. June 16-21， 2002， San Antonio， TX， USA. IEEE， 2002： 314-317.

[25] 张公凯， 陈才学， 郑拓. 改进鲸鱼算法在电动汽车有序充电中的应用[J]. 计算机工程与应用， 2021， 57（4）： 272-278.

ZHANG G K， CHEN C X， ZHENG T. Application of improved whale optimization algorithm in ordered charging of electric vehicle [J]. Computer Engineering and Applications， 2021， 57（4）： 272-278. （in Chinese）

[26] 冯一凡， 毛毳. 斜拉索覆冰形态试验研究[J]. 天津城建大学学报， 2019， 25（1）： 20-25.

FENG Y F， MAO C. Research on the model of ice accretion on inclined cable [J]. Journal of Tianjin Chengjian University， 2019， 25（1）： 20-25. （in Chinese）

[27] 朱永燦. 架空输电线路覆冰生长模型及其关键参数研究[D]. 西安： 西安电子科技大学， 2017.

ZHU Y C. Research on the icing growth model and key parameters on overhead transmission lines [D]. Xian： Xidian University， 2017. （in Chinese）

（编辑 王秀玲）