自锚式悬索桥断索动力冲击效应模型试验研究

叶毅 任阳阳 邓余杰 陈鹏飞 郭琦

摘 要：為探讨自锚式悬索桥在吊索瞬时破断作用下的动力冲击效应，以某在役自锚式悬索桥为背景，基于刚度相似理论建立1∶80的缩尺试验模型，进行不同区段内吊索的断索动力冲击效应模型试验。试验结果表明：不同区段吊索破断引起的冲击效应不同;断索会引起与破断吊索同侧同跨的相邻吊索区域内的动态内力重分布且动力冲击效应明显;与瞬断吊索紧邻的两根吊索中，较长吊索的动力冲击系数（DIF）和动力放大系数（DAF）均较大，其动力冲击效应和冲击作用敏感性更高;瞬断工况下的吊索拉力动态响应峰值较断索前普遍达到2倍以上，吊索的安全储备明显较低。相邻吊索在断索作用下的动力冲击效应显著，若相邻吊索存在腐蚀等缺陷，极易导致桥梁连续性断索，严重影响桥梁安全。

关键词：自锚式悬索桥;缩尺模型试验;吊索瞬断;动力冲击效应;桥梁安全

中图分类号：U446.1   文献标志码：A   文章编号：2096-6717（2022）03-0001-09

收稿日期：2020-10-28

基金项目：国家自然科学基金（51508453）;陕西省教育厅科研计划（14JK1418）

作者简介：叶毅（1981- ），男，博士，主要从事现代桥梁结构设计理论、桥梁结构损伤评估研究，E-mail： no-yy@163.com。

Received：2020-10-28

Foundation items：National Natural Science Foundation of China （No. 51508453）; Research Project of Shaanxi Provincial Department of Education （No. 14JK1418）

Author brief：YE Yi （1981- ）， PhD， main research interests： modern bridge structure design theory， bridge structure damage assessment， E-mail：no-yy@163.com.

Model testing research of impact effect on self-anchored suspension bridge subjected to hangers fracture

YE Yi ， REN Yangyang1a， DENG Yujie1a， CHEN Pengfei 2， GUO Qi

（1a. School of Civil Engineering; 1b. Key Lab of Structural Engineering and Earthquake Resistance， Ministry of Education （XAUAT）， Xian University of Architecture & Technology， Xian 710055， P. R. China; 2. Zhejiang Communications Construction Group Co.， Ltd.， Hangzhou 310051， P. R. China）

Abstract： In order to examine the dynamic impact effect of the self-anchored suspension bridge subjected to hangers fracture， model test for suspension hangers fracture was carried out.A 1∶80 test model was developed based on the stiffness similarity theory. The test results indicate： the dynamic impact effects of hangers fracture in different regions are dissimilar. The tensile forces of the adjacent hangers on the same-side and same-span are dynamically redistributed after hangers fracture. Compared with shorter hanger that is adjacent to the broken suspension hanger， the Dynamic Impact Factor（DIF） and the Dynamic Amplification Factor（DAF） of the longer one is greater.The dynamic impact effect is obvious and dynamic impact sensitivity is higher. The peak values of dynamic tension forces of the hangers would be more than twice of the original values generally， and the safety reserve is obviously reduced. The dynamic impact effects of hangers fracture is significant， and it will lead to continuous hangers fracture easily on occurrence of corrosion or other defects of the adjacent hangers and affects the safety of bridges seriously.

Keywords：self-anchored suspension bridge; scale model test; hanger fracture; dynamic impact effect; bridge safety

吊索是自锚式悬索桥主缆与加劲梁之间传递荷载的关键受力构件[1]。在桥梁的运营期间，由于环境腐蚀和交变应力的耦合作用，高应力状态下的吊索易发生损伤甚至断裂[2-4]。近年来，在役桥梁逐渐进入维修加固期，缆索体系桥梁的吊索损伤隐患突增，严重影响大桥的运营安全[5]。针对拉吊索瞬断对剩余构件动力冲击效应的影响规律，一些学者开展了研究并取得了一定的研究成果。

Ruiz-Teran等[6]对斜拉桥拉索瞬断后剩余构件的力学响应进行了分析，结果表明，拉索的动力放大系数DAF（动力响应增量/静力响应增量）存在大于2的情况，超出当时桥梁设计规范所规定的最值;Wolff等[7]针对斜拉索的破断动力效应进行了研究，结果表明，采用动力放大系数DAF进行简化计算具有一定的可行性，但仍建议采用动力时程方法分析关键吊索的动力效应;Cai等[8]对斜拉桥拉索破断的非线性反应进行了研究，发现相邻两根拉索的同时断裂会引起其他拉索屈服和塑性变形;叶毅等[9]通过研究自锚式吊拉协作体系的端吊索破断对结构受力性能的影响，发现吊索瞬断引起的结构位移、内力以及缆索系统内力在其静态效应附近剧烈振荡并逐渐稳定于静态效应;邱文亮等[10]比较了自锚式悬索桥在不同吊索形式下单根吊索破断后桥梁结构的响应规律，验证了采用双吊索可以大幅度降低断索后桥梁结构的响应。

对于结构模型试验方法的研究，已有学者进行尝试，并取得了较理想的成果。黄维平等[11]发现，砌体结构模型在配重不足的条件下可以用量纲分析法或方程法推导其动力相似关系;项贻强等[12]针对斜拉桥等组合体系桥梁结构，基于刚度相似原理，提出了结构中存在两种弹性模量相似比时的模型设计与制作方法。洪彧等[13]总结了桥梁模型试验的研究进展，对缆索系统模型试验进行了系统性的介绍，但仍缺乏对断索工况下桥梁结构的动力过程试验研究。

由于大跨度桥梁缩尺模型试验成本高、周期长、动力相似关系复杂，关于自锚式悬索桥的桥梁断索动力冲击效应的研究大都侧重于理论算法以及数值模拟分析，缺乏模型试验对理论分析结果的验证和支撑，进行试验测试对明晰实际断索时的动力冲击效应及其程度具有一定实际意义。笔者基于某在役混凝土自锚式悬索桥，在满足“刚度相似且应变相等”[12]的要求下，根据试验条件对理想缩尺模型参数进行部分调整，设计并制作了一座1∶80缩尺试验模型进行试验。将缩尺试验模型和数值模型进行对比分析和验证，对典型吊索破断后剩余吊杆内力重分布的冲击效应进行分析。

1 试验模型

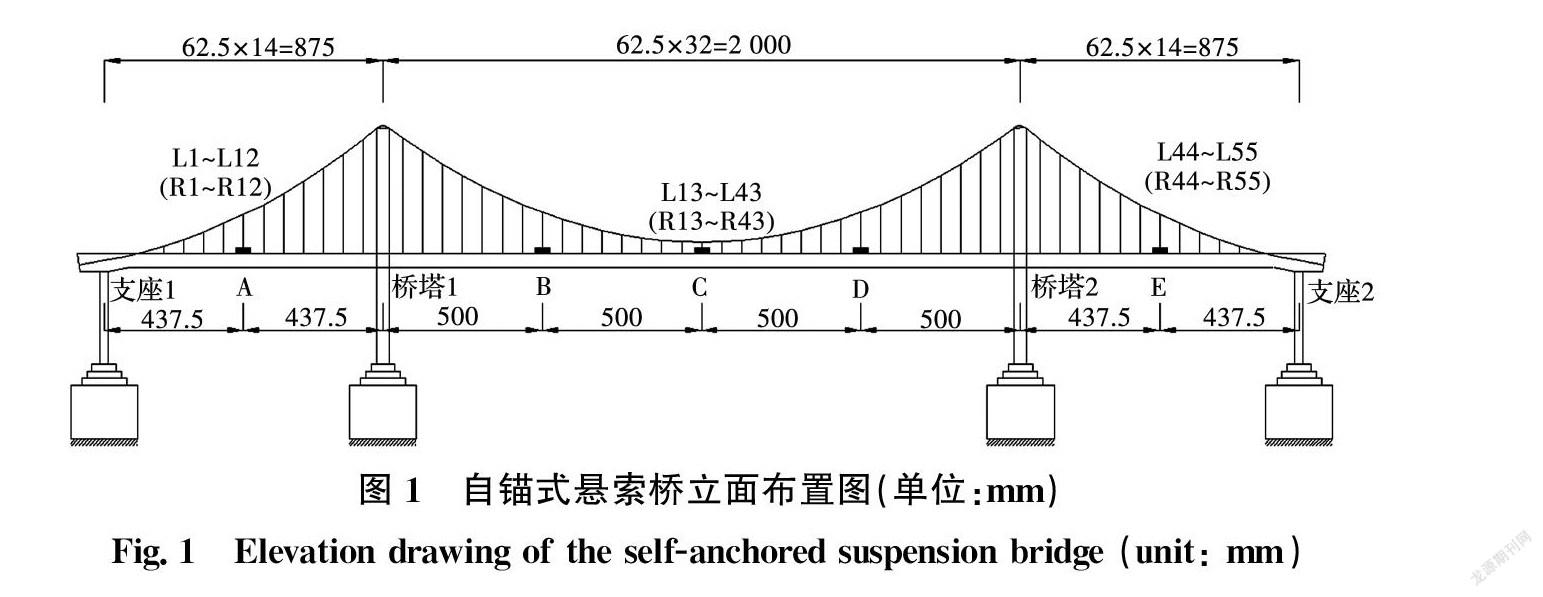
以某在役混凝土自锚式悬索桥为工程背景，桥长330 m，跨径布置为15 m+70 m+160 m+70 m+15 m，中跨主缆垂跨比为1/6。在缩尺试验模型的设计过程中充分考虑试验所要达成的目的并忽略次要参数进行分析。试验中按照几何相似和刚度相似的原则对模型构件截面和形式进行简化处理。主梁截面简化为体内布置钢丝网的带肋C15混凝土板，板厚23 mm，板宽360 mm，吊索锚固区板厚增至40 mm;桥梁锚固跨简化为梁上重力式压块。主缆横截面积为28.26 mm2，其钢绞线标准抗拉强度为1 960 MPa;吊索横截面积为0.68 mm2，其标准强度为1 670 MPa;主缆和吊索均采用无应力长度进行索力控制。吊索沿顺桥向以62.5 mm等间距布置，吊索上端采用马蹄形索夹与主缆连接，下端采用螺杆与主梁锚固，吊索编号沿顺桥向依次为L1#～L55#和R1#～R55#，缩尺模型结构尺寸及吊索编号如图1所示。

缩尺试验实际模型的设计与制作面临的主要问题是缩尺后构件尺寸过小和理想模型所用的材料容重过大。由于混凝土的特性决定了设计尺寸过小的构件无法浇筑，试验中按照“等效刚度相似”的原则对模型构件截面形式进行简化设计处理。针对缩尺模型材料容重不足的问题，对主梁和主缆结构进行配重处理。对于缩尺试验模型的几何尺寸所导致的难以足额配重的问题，考虑到缩尺模型试验的目的是验证断索后桥梁结构的动力行为特征，缩尺试验模型主梁的配重采用其理论值的1/10进行试验。按照上述方案建立自锚式悬索桥测试结构体系的缩尺试验模型，同时，建立相对应的有限元数值模型，以进行理论研究和试验验证，自锚式悬索桥缩尺试验模型如图2所示。

2 吊索破断对剩余吊索的影响

为确定缩尺模型试验中采用的断索工况，针对原桥结构，采用数值模拟的方式对各损伤工况下剩余吊索的变化情况进行分析。采用ANSYS分析軟件建立自锚式悬索桥三维有限元模型，利用Beam4单元模拟主梁和索塔，利用Link10单元模拟主缆和吊索[14]，主梁与桥塔均选用C50混凝土。模型中的主梁采用鱼骨梁的形式进行模拟。模型纵向主刺的截面特性按自锚式悬索桥的实际主梁截面确定;主刺两侧为刚性臂，用于模拟主梁与吊索之间的连接，以起到传递荷载的作用。塔架底部采用固结约束，吊索和主缆的初始应力通过赋值初始应变施加。吊索动力破断分析采用瞬态分析方式进行：首先，定义结构瞬态分析所需的环境变量数据，包括分析方法、Rayleigh阻尼系数等;其次，在结构上施加重力加速度，对桥梁结构进行自重作用下的静力分析;然后，依据吊索的具体破断工况，借助ANSYS中的“单元生死”功能，在0.002 s内将对应吊索单元进行“杀死”，并进行瞬态动力分析;最后，利用时间历程后处理器提取各类响应数据。根据吊索破断后结构应变能变化和吊索位置等情况，选取L6#、L12#、L13#、L20#号吊索作为研究对象进行分析。

2.1 单根吊索破断

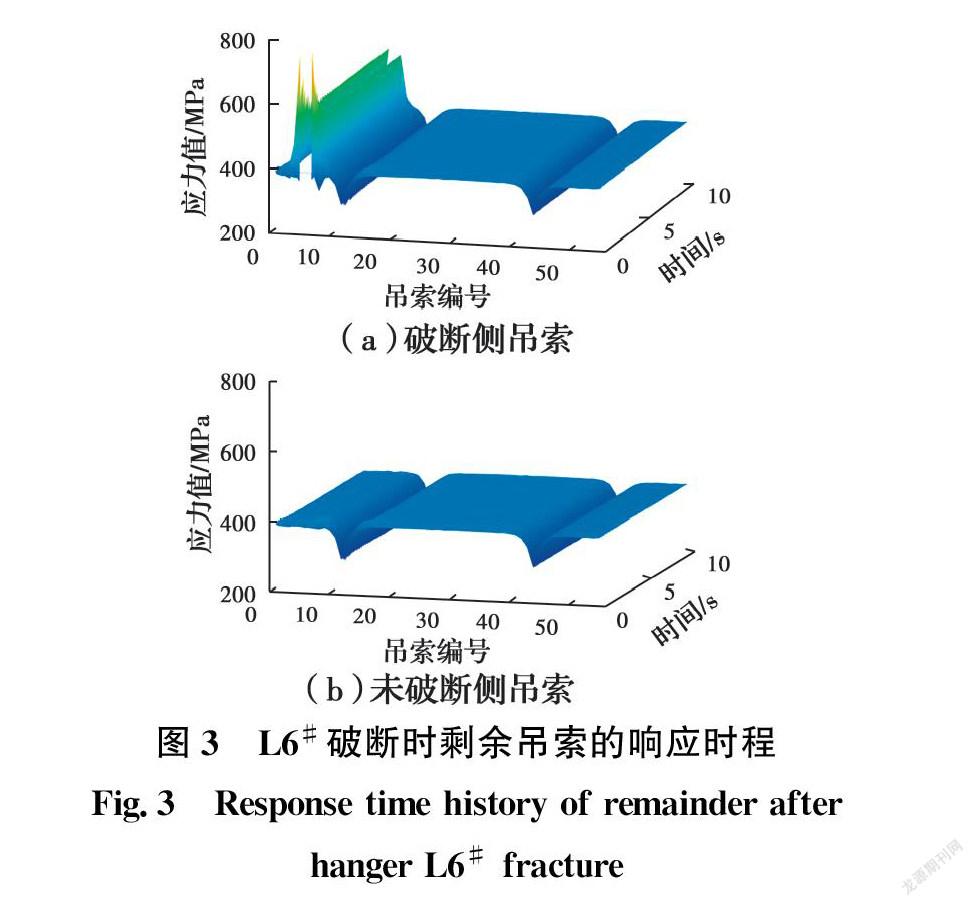
图3给出了在L6#吊索发生瞬断后10 s内剩余吊索的应力响应时程情况。可见，L6#吊索瞬断后，与其相邻的两三根吊索的应力剧烈振荡后趋于稳定，而其他吊索的应力则无明显变化。

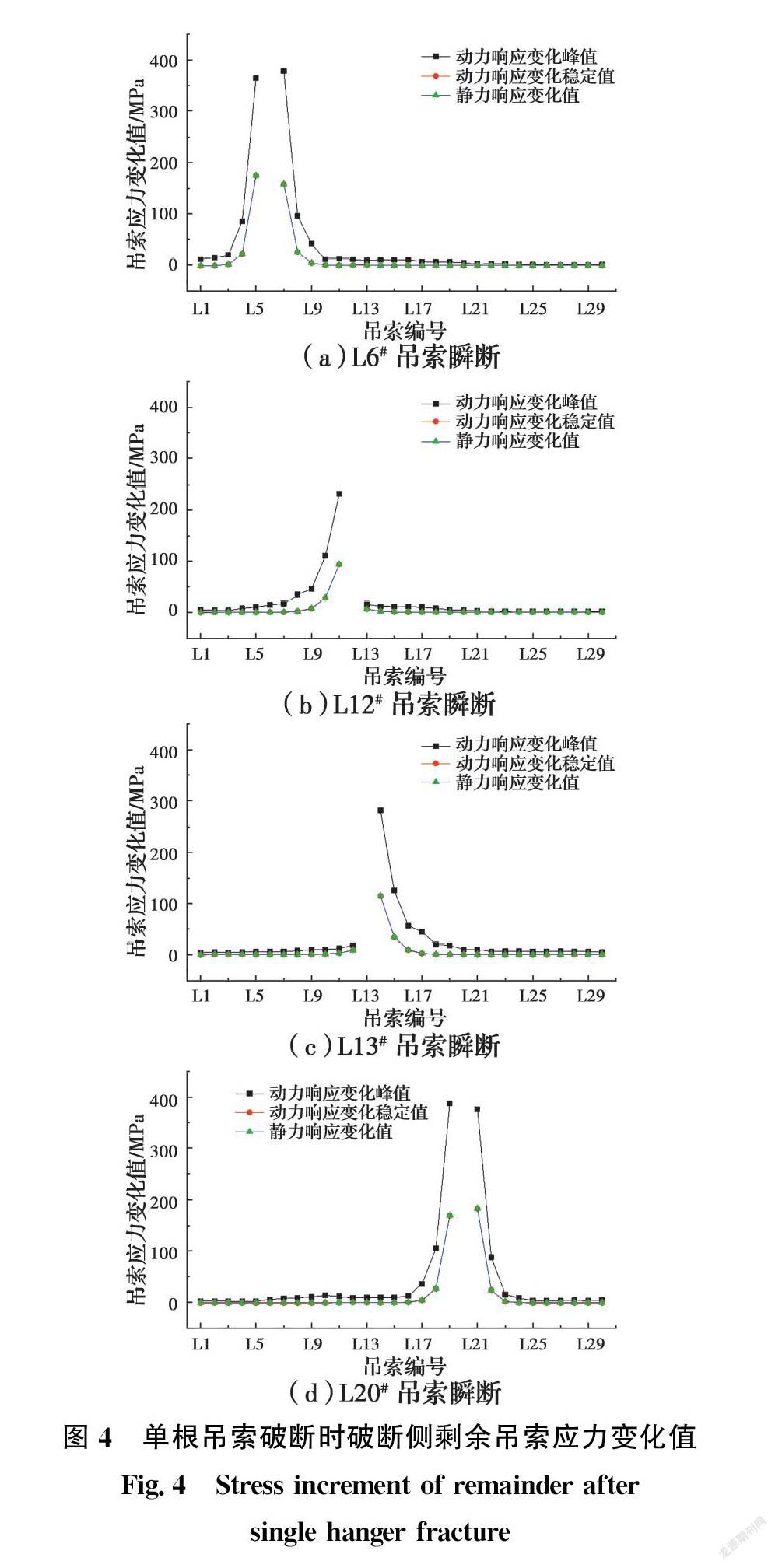
图4中给出了在单根吊索破断工况下破断侧部分剩余吊索的应力变化值。结合图3、图4可知，单根吊索破断后，仅破断侧与破断吊索同跨相邻两三根吊索的应力增量较大且与之紧邻吊索最为显著，说明随着与破断吊索距离的增加，剩余吊索的应力响应急剧减弱。同时可以看出，仅与破断吊索同跨相邻的吊索动力响应变化峰值增量与静力响应变化值差距较大，而其动力响应变化稳定值增量则与静力响应变化值相近。如L6#吊索瞬断工况下，L5#和L7#吊索应力的动力响应变化峰值增量分别为372.4、382.55 MPa。与其静力响应变化值174.87、158.12 MPa相比，其动力响应增量明显较大，说明与破断吊索相邻的剩余吊索在吊索瞬断工况下的动力冲击效应显著。

剩余吊索应力变化情况可知：L20#吊索瞬断时，L19#吊索应力变化峰值增量为394.7 MPa（增幅99.7%）;而L12#吊索瞬断时，L11#吊索应力变化峰值增量为230.2 MPa（增幅58.1%），说明不同位置吊索破断引起的冲击效应不同。对比两根与桥塔紧邻的吊索破断后剩余吊索的应力变化情况可知：L12#吊索瞬断时，L11#吊索应力变化峰值增量为230.2 MPa（增幅58.1%）;而L13#吊索仅增加了16.59 MPa（增幅4.7%）;同样，L13#吊索瞬断时，L14#吊索应力增幅为70.9%，而L12#吊索仅为2.9%。表明吊索破断仅对与之同跨同侧的相邻吊索产生影响。

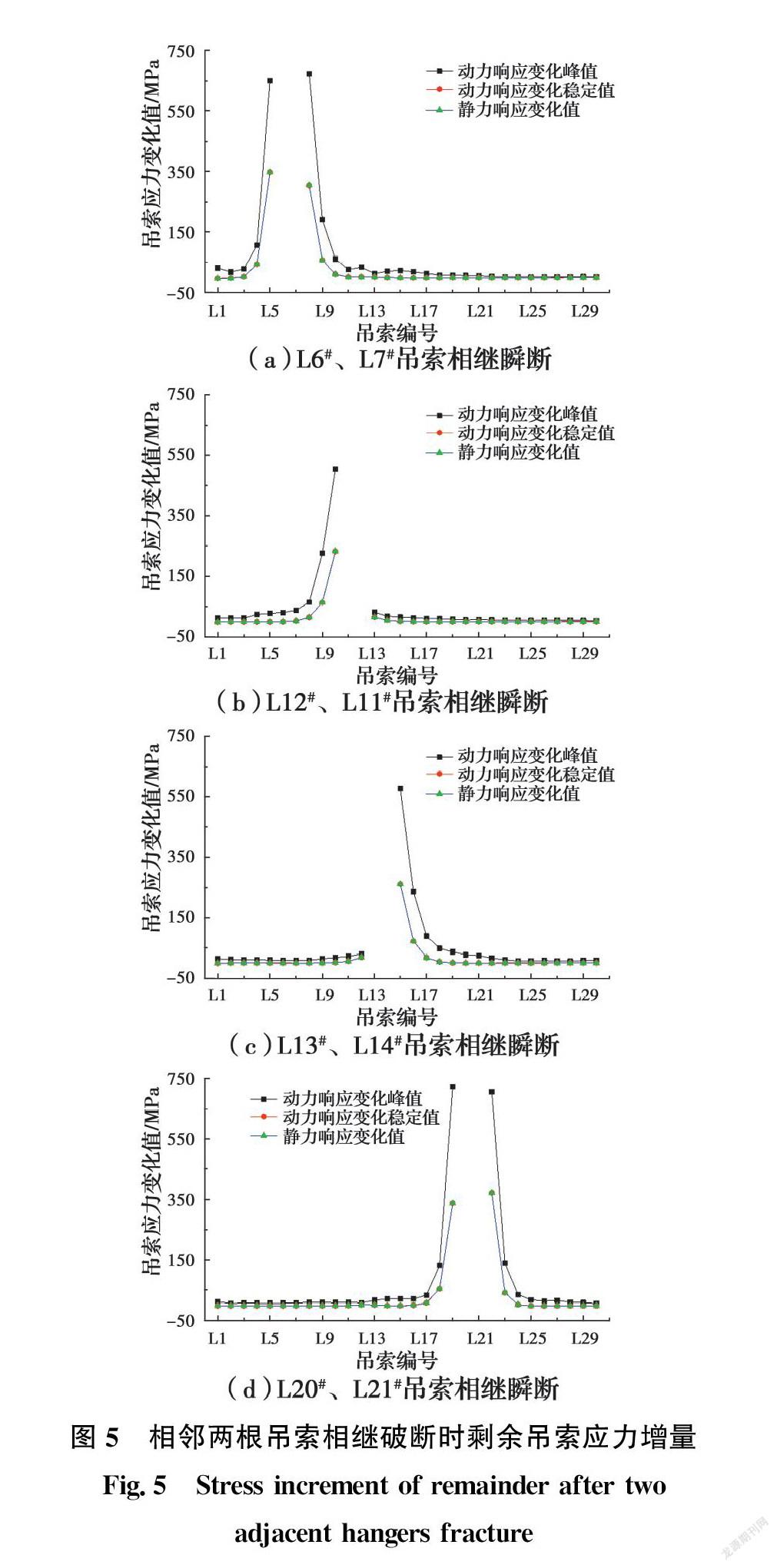
2.2 相邻两根吊索破断

图5中给出了相邻两根吊索相继破断后，破断侧剩余吊索的应力变化情况。

L6#和L7#吊索相继破断时，L5#和L8#吊索应力动力响应变化峰值增幅分别为163.0%和173.4%，其静力响应增幅仅为87.3%和76.4%，且其动力响应变化稳定值增幅与静力响应相近;L12#和L11#吊索相继破断时，仅与其同跨的L10#吊索应力增幅达131.4%。表明相邻两根吊索破断存在动力冲击效应随传播距离的增加而急剧减弱的现象，且仅对与之同跨同侧相邻吊索有较大影响。同时，相邻两根吊索破断引起的剩余吊索动力冲击效应更剧烈。

3 试验方案

3.1 加载方案

运用吊索破断试验验证不同吊索破断工况下结构响应的动力放大效应和差异特征。

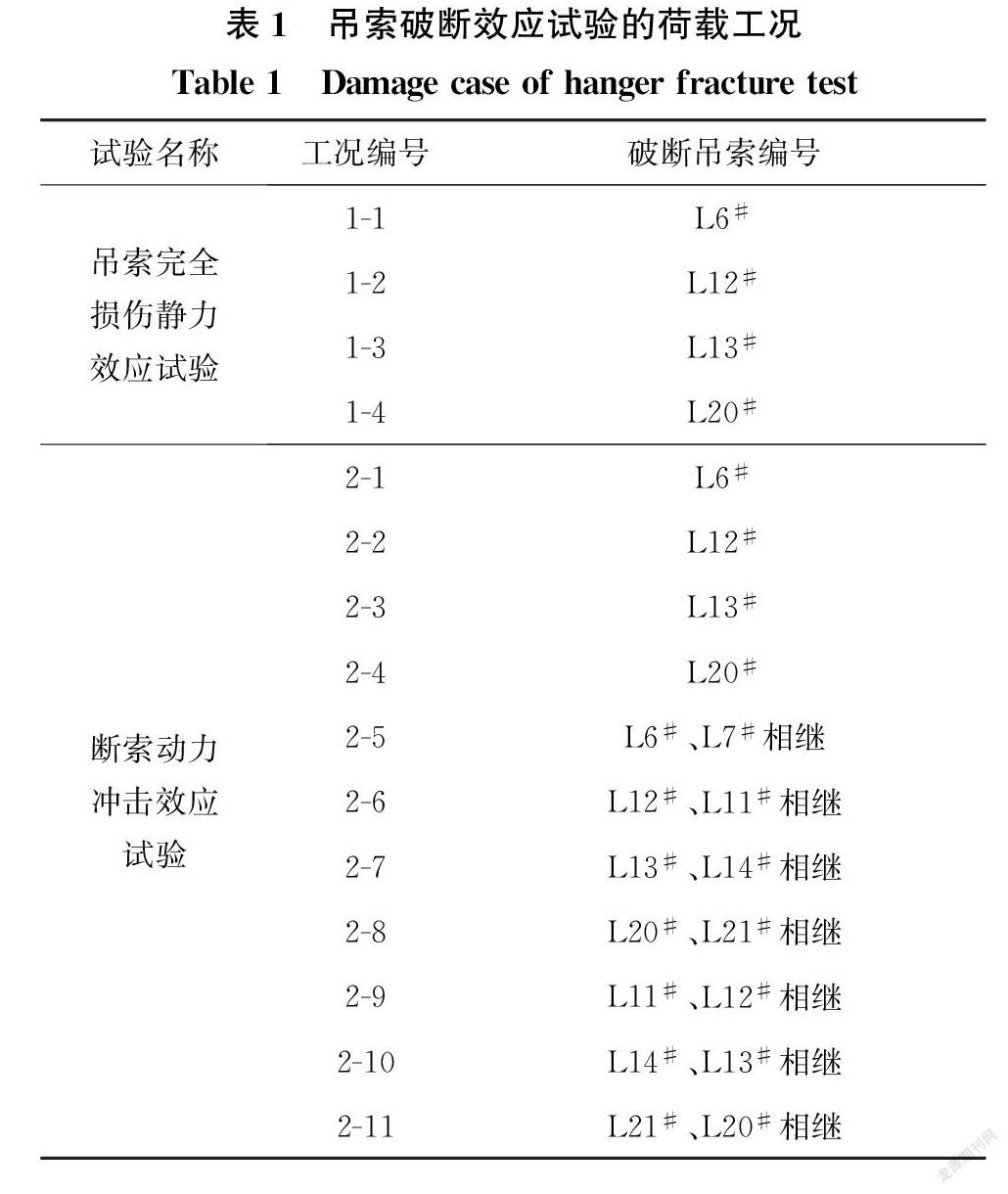
测试工况设置如表1所示。模型试验分为吊索完全损伤静力效应试验和断索动力冲击效应试验两部分，吊索完全损伤静力效应试验是为了验证静力断索后其余结构的静力学变化规律。通过对比各断索工况试验值与理论计算值，验证缩尺试验模型与缩尺数值模型的吻合性，吊索静力完全损伤测试工况采用缓慢放松吊索下部锚固装置进行模拟。断索动力冲击效应试验是为了通过实际测试来验证断索动力冲击效应规律，并通过引入冲击效应和断索敏感性的量化评价指标对断索动力冲击效应进行分析，吊索瞬断测试工况采用剪刀瞬间切断对应吊索的方式进行模拟。

3.2 测试装置布置

如图6（a）、（b）所示，依据吊索和主缆的力学特点设置各索力测试系统。吊索动态拉力是通过串联在吊索中的S型拉压力传感器测得，主缆拉力采用穿心式压力传感器在主缆锚固构造处测得。由于动态数据采集仪通道数的限制，吊索拉力测试的数据采集点选择破断吊索附近响应较为剧烈的部分作为采集对象，即当Li#吊索破断时，吊索拉力测试装置布置在Li-3#、Li-2#、Li-1#、Li+1#、Li+2#、Li+3#、Ri-1#、Ri#和Ri+1#吊索处。测试系统能够测量动态实时索力。如圖6（c）所示，主梁挠度动态数据采用拾振器进行数据采集，测试位置主要布置于各跨跨中以及破断吊索处。

4 试验结果及数据分析

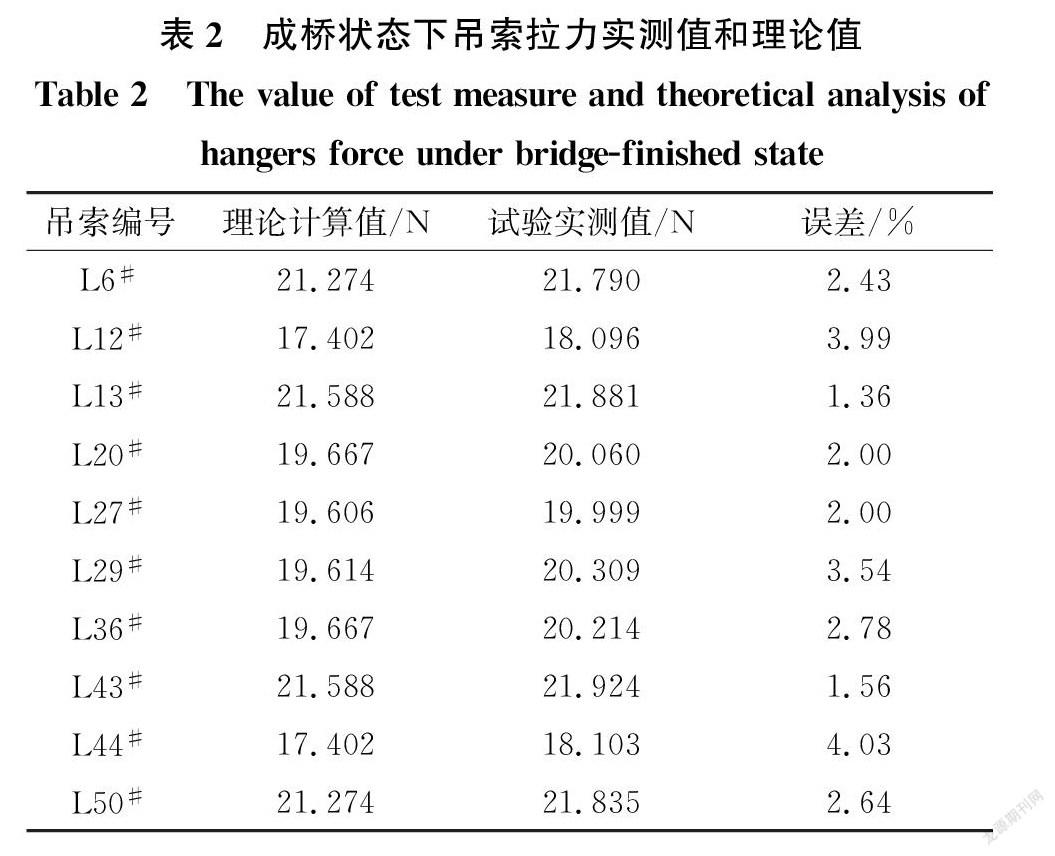
在吊索张拉过程中，基于自锚式悬索桥结构的对称性，选取了各跨跨中、桥塔两侧、中跨1/4处等10个典型位置的吊索并设置拉力测试装置来测量成桥状态下各吊索的拉力值，并利用缩尺试验模型对应的数值模型分析成桥状态下各吊索拉力的理论值。

由表2可知，缩尺试验模型各测点的拉力实测值与其对应的数值模型拉力理论值较为接近，误差为1.36%～4.03%，说明试验模型制作与数值模型吻合良好。

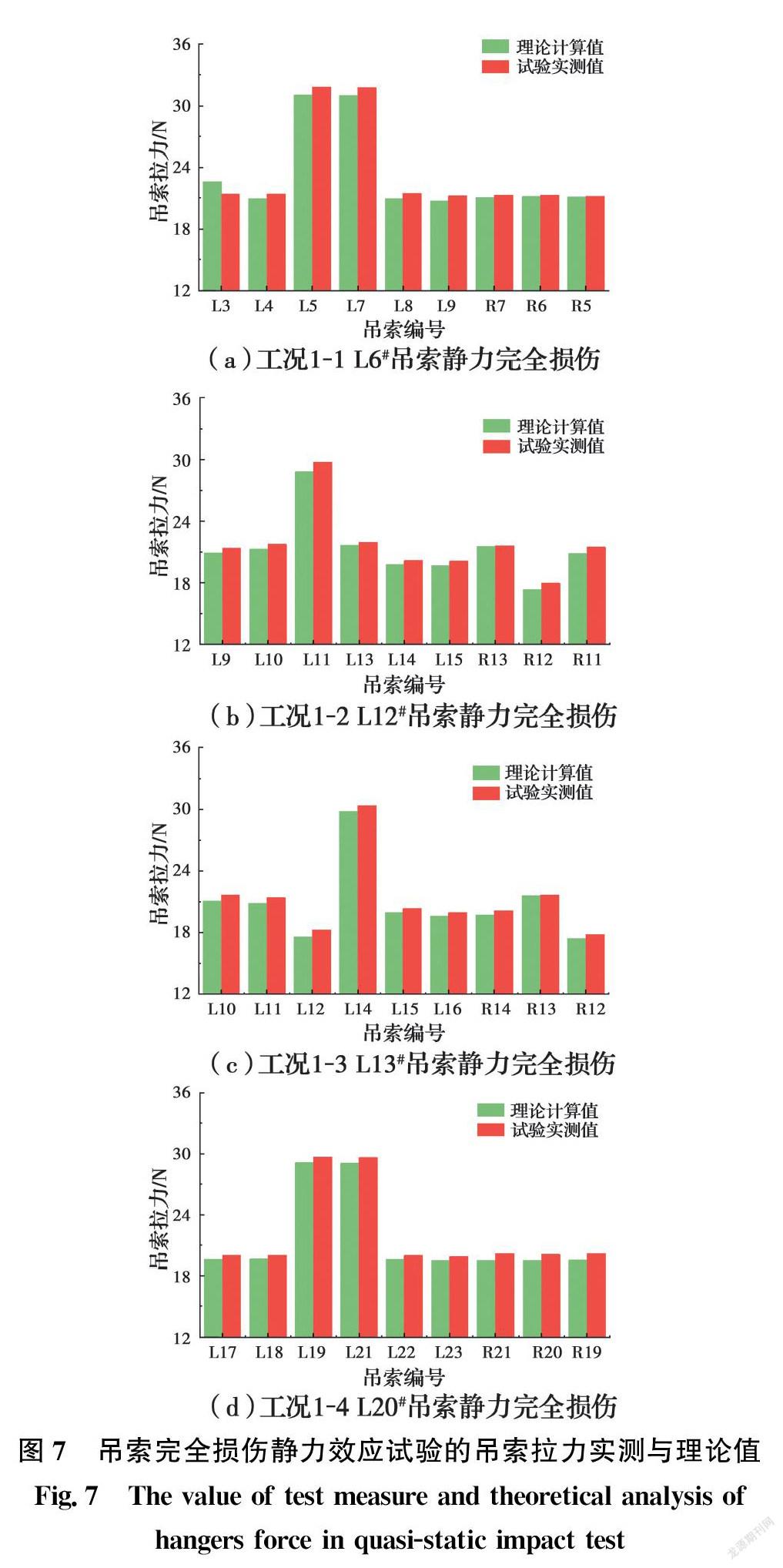
4.1 吊索完全损伤静力效应试验

吊索完全损伤静力效应试验中拉力实测值与计算值的对比情况如图7所示，由图可知，静力断索实测值与理论值间的误差均在5.5%以下，且拉力变化规律相同。L6#吊索静力完全损伤工况下，L5#和L7#吊索的拉力增量分别为10.581、10.496 N，其他测点吊索的拉力增量则小于1 N;L20#吊索发生静力完全损伤时具有类似规律。该现象表明：

吊索的静力完全损伤只对破断侧与其相邻的吊索拉力具有较大影响。L12#吊索静力完全损伤工况下，L11#吊索的拉力增量为29.740 N，而L13#吊索的拉力无明显变化;L13#吊索静力完全损伤工况也具有类似规律。该现象进一步表明：与损伤吊索同跨的破断侧吊索主要参与了损伤后吊索拉力的重分布，该规律与原桥静力完全损伤的理论分析结果相符，验证了缩尺试验模型及其测试的合理性。

4.2 断索动力冲击效应试验

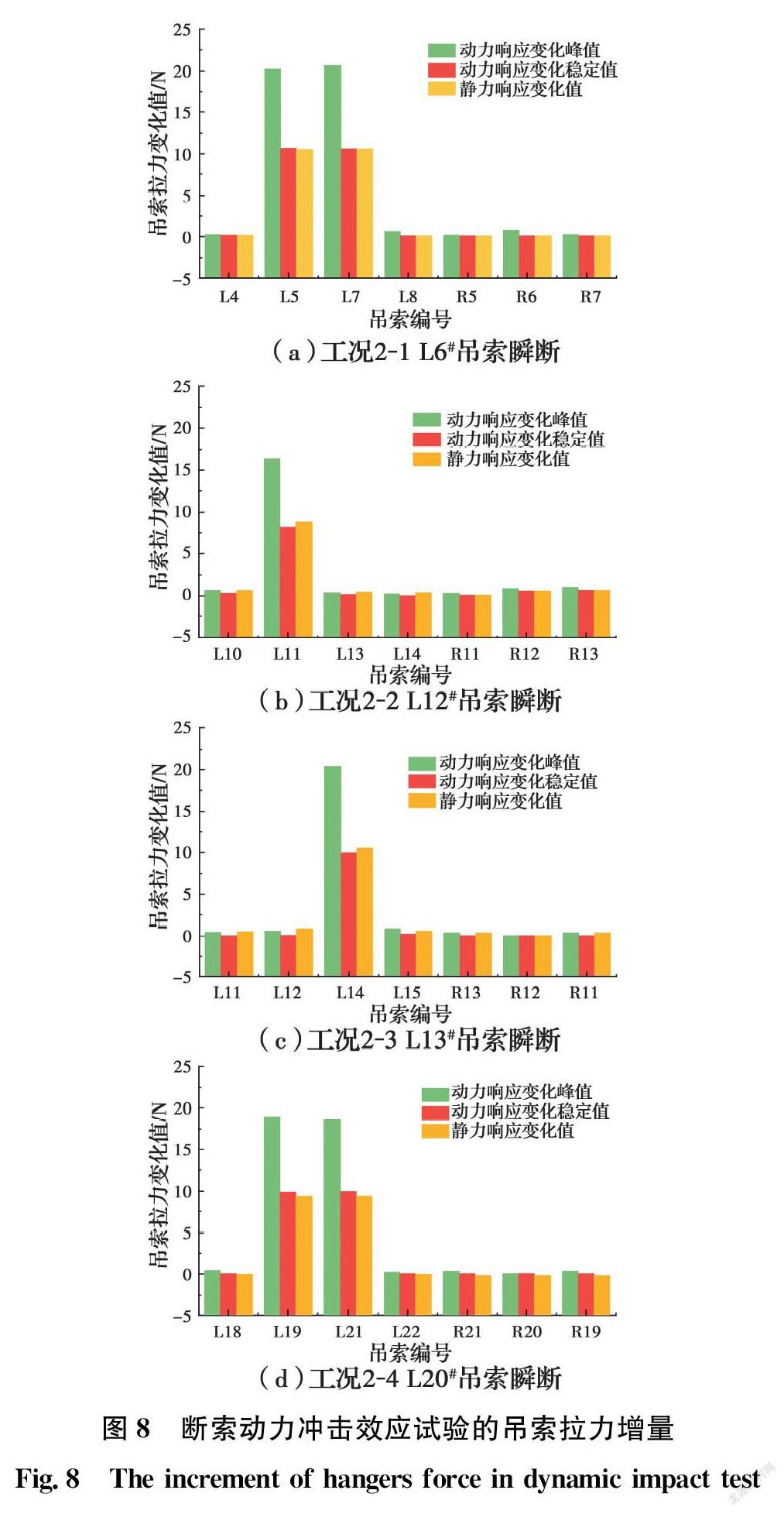
断索动力冲击效应试验是通过测试相邻几根吊索拉力的实时变化值来研究缩尺模型中吊索的动力响应变化规律。工况2-1～2-4探讨了单根吊索瞬断工况下剩余吊索的响应规律，其索力增量如图8所示。L6#吊索瞬断工况下，L5#和L7#吊索拉力的动力响应稳定值增量与静力响应相近，而动力响应峰值增量显著大于静力响应;L20#吊索瞬断时表现相同。L12#吊索瞬断工况下，与其同跨相邻的L11#吊索拉力大幅度增加，而与其邻跨的L13#吊索的拉力变化甚微;L13#吊索瞬断时表现相同。结果表明：吊索发生瞬断，冲击作用仅在破断侧与其同跨紧邻的吊索产生内力重分布效应，而对其余吊索影响甚微。断索冲击效应试验结果与上文中的理论分析相比，影响范围缩小至与破断吊索紧邻的吊索，但依然满足其相应的吊索内力重分布和冲击效应规律。

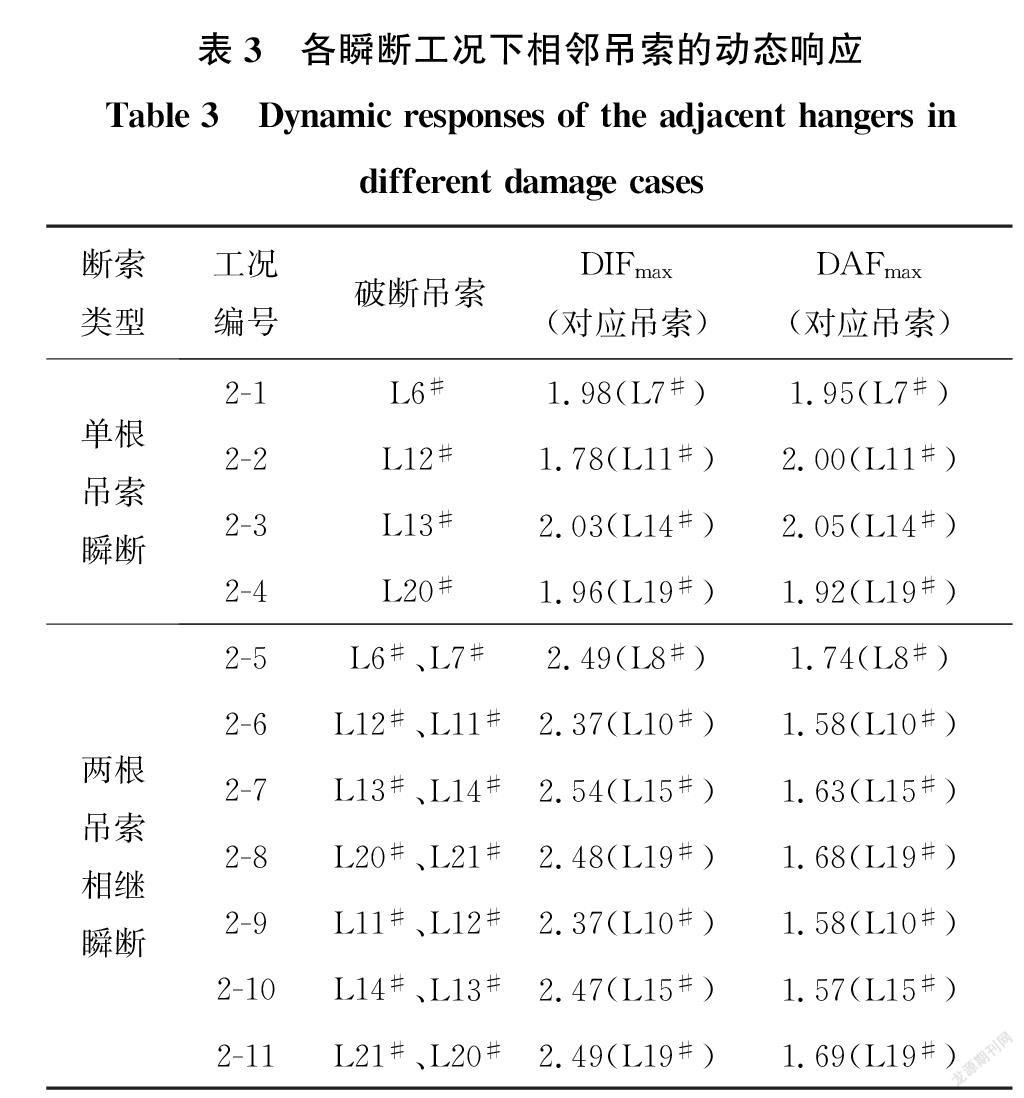
工况2-5～2-11探讨了多根吊索瞬断对剩余吊索内力的影响。为定量分析断索动力冲击效应，引入动力冲击系数DIF（动力响应值/断索前响应值）和动力放大系数DAF（动力响应增量/静力响应增量）[15]作为冲击效应和断索敏感性的量化评价指标，并将各工况下的构件对断索的响应值进行分析和比较，探究自锚式悬索桥构件在突然断索工况下的动力冲击效应。DIF可以用来描述动力冲击作用引起结构内力变化的程度，反映动力冲击效应的影响程度。DAF可用来反映剩余吊索对断索动力冲击效应的敏感性，DAF越大，表明构件对断索动力冲击效应越敏感。为定量分析断索动力冲击效应的大小，将各瞬断工况下紧邻吊索的量化评价指标列于表3。

由表3可知，不同区段的吊索破断引起的冲击效应不同，相邻两根吊索相继破断的动力冲击效应更为显著。同时，与瞬断吊索紧邻的两根吊索中较长者的DIF值和DAF值均较大，其动力冲击效应和敏感性更高。这是由于这两根吊索均与主缆和主梁连接，其耦合效应使得在内力重分布时较长的吊索具有较大的动力冲击效应和较高的敏感性。

总的来看，与瞬断吊索紧邻的吊索拉力的动力放大系数最大值DAFmax均超过了1.5，其中部分断索工况下大于PTI（the Post-Tensioning Institute）针对斜拉桥推荐的限值2.0[16]，吊索内力对断索的动力响应明显。现行行业标准[17]要求一般公路悬索桥吊索抗拉强度验算的销接式吊索材料强度分项系数取2.2，现有大型悬索桥的安全系数普遍取值为3以上。在断索动力冲击效应试验中，单吊索破断时相邻吊索的动态拉力响应峰值普遍为断索前拉力的2倍，即动力冲击系数最大值DIFmax维持在2左右，相邻两根吊索相继破断更是普遍达到2.5，自锚式悬索桥吊索的安全储备明显降低。自锚式悬索桥吊索的瞬断对相邻吊索的安全构成了一定威胁，如果在吊索破断的同时，相邻吊索存在腐蚀、疲劳损伤等所引起的承载力下降现象，突然断索可能会引起相邻吊索相继断裂，进而有可能引起更多吊索断裂，甚至全桥垮塌。

4.3 主梁挠度和主缆锚固力的测试

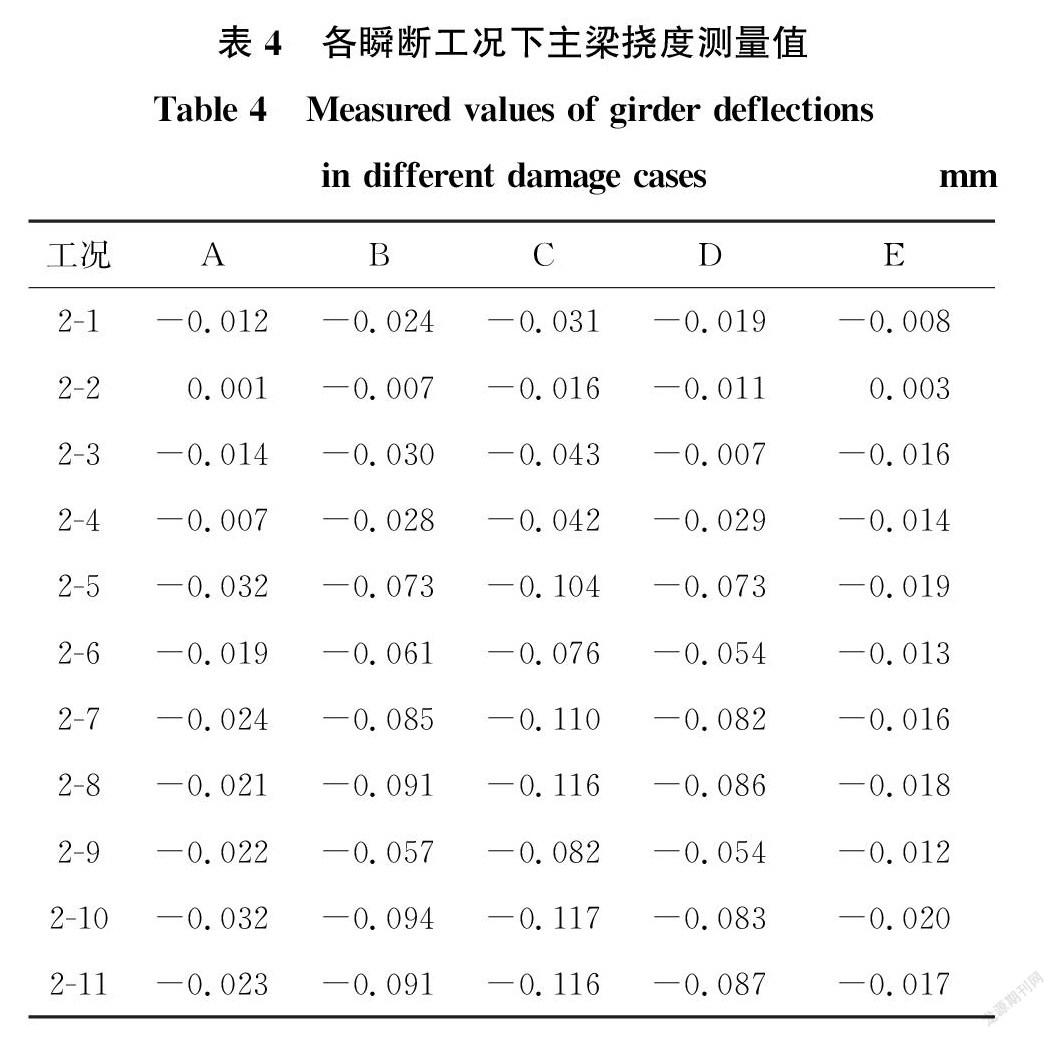
在进行索力测试的同时，采用穿心式压力计和拾振器对主缆锚固力和主梁挠度进行测试。主梁挠度测试中各测点从左向右编号依次为A～E，如图1所示。表4中给出了主梁在各工况下挠度的变化情况。

各断索工况下主梁撓度增量大小的规律大致为：中跨跨中位置处最大，其次为中跨1/4位置处，最小处为边跨跨中。中跨两根吊索相继破断工况下主梁挠度的增量最大值仅为0.117 mm，这是由于自锚式悬索桥采用刚性主梁，主梁刚度承担了断索作用下的部分弯矩。同时，缩尺试验模型的主缆拉力变化幅值仅为5%，吊索破断对主缆和主梁的影响较低。

5 结论

基于相似理论，设计并制作了某在役自锚式悬索桥的缩尺试验模型，并通过对比模型吊索完全损伤的试验测试值和其有限元数值模型的分析预测值，验证模型试验的合理性。通过对桥梁模型在不同断索工况下吊索的力学响应测试与分析，探索了自锚式悬索桥结构的力学响应规律和动力冲击效应，得到以下结论：

1）断索会引起与破断吊索相邻区域内吊索的动态内力重分布，与破断吊索紧邻的吊索动力冲击效应明显。不同区段吊索破断引起的冲击效应不同，相邻两根吊索相继破断的动力冲击效应更为显著。

2）吊索瞬断工况下，与瞬断吊索相邻的两根吊索中较长者的DIF值和DAF值均较大，其动力冲击效应更显著、冲击作用敏感性更高。相邻吊索的动态拉力响应峰值较断索前普遍会达到2倍以上，DIFmax最大可达2.54倍。现行行业标准要求一般公路悬索桥吊索抗拉强度验算的销接式吊索材料强度分项系数取2.2，而对于自锚式悬索桥而言，吊索的安全储备明显较低。

3）建议自锚式悬索桥吊索在设计阶段应考虑吊索瞬断时产生的冲击效应并提高吊索的能力需求比，增加相应吊索的安全储备，可适当增大安全系数至2.5以上，在运营阶段加强对相邻吊索的实时联合监测。参考文献：

[1] 袁毅， 易伦雄. 武汉古田桥： 自锚式悬索桥设计及关键技术[J]. 桥梁建设， 2019， 49（2）： 80-85.

YUAN Y， YI L X. Design and key techniques of Gutian self-anchored suspension bridge in Wuhan [J]. Bridge Construction， 2019， 49（2）： 80-85. （in Chinese）

[2] 杨世聪， 张劲泉， 姚国文. 在役桥梁拉吊索腐蚀-疲劳损伤与破断机理分析[J]. 公路交通科技， 2019， 36（3）： 80-86.

YANG S C， ZHANG J Q， YAO G W. Analysis on corrosion-fatigue damage and fracture mechanism of cables/hangers in service bridges [J]. Journal of Highway and Transportation Research and Development， 2019， 36（3）： 80-86. （in Chinese）

[3] 乔燕， 缪长青， 孙传智. 索承式桥梁吊索钢丝腐蚀疲劳寿命评估[J]. 土木建筑与环境工程， 2017， 39（4）： 115-121.

QIAO Y， MIAO C Q， SUN C Z. Evaluation of corrosion fatigue life for corroded wire for cable-supported bridge [J]. Journal of Civil， Architectural & Environmental Engineering， 2017， 39（4）： 115-121. （in Chinese）

[4] 孟二从， 姚国文， 余亚琳， 等. 服役环境下镀锌钢丝力学性能影响因素分析[J]. 建筑材料学报， 2020， 23（4）： 934-940.

MENG E C， YAO G W， YU Y L， et al. Influence factor analysis on the mechanical behavior of galvanized steel wire under service environment [J]. Journal of Building Materials， 2020， 23（4）： 934-940. （in Chinese）

[5] 朱利明， 钱思沁， 陈沁宇， 等. 在役桥梁垮塌风险评估及预防策略[J]. 南京工业大学学报（自然科学版）， 2020， 42（3）： 284-290.

ZHU L M， QIAN S Q， CHEN Q Y， et al. Risk assessment and prevention strategy of bridge collapse in service [J]. Journal of Nanjing Tech University （Natural Science Edition）， 2020， 42（3）： 284-290. （in Chinese）

[6] RUIZ-TERAN A M， APARICIO A C. Dynamic amplification factors in cable-stayed structures [J]. Journal of Sound and Vibration， 2007， 300（1/2）： 197-216.

[7] WOLFF M， STAROSSEK U. Cable loss and progressive collapse in cable-stayed bridges [J]. Bridge Structures， 2009， 5（1）： 17-28.

[8] CAI J G， XU Y X， ZHUANG L P， et al. Comparison of various procedures for progressive collapse analysis of cable-stayed bridges [J]. Journal of Zhejiang University Science A， 2012， 13（5）： 323-334.

[9] 葉毅， 张哲， 李文武， 等. 自锚式吊拉协作体系桥端吊索破断效应[J]. 沈阳建筑大学学报（自然科学版）， 2013， 29（3）： 412-418.

YE Y， ZHANG Z， LI W W， et al. Fracture effects analysis of end hanger of self-anchored cable-stayed suspension bridge [J]. Journal of Shenyang Jianzhu University （Natural Science）， 2013， 29（3）： 412-418. （in Chinese）

[10] 邱文亮， 吴广润， 张哲， 等. 突然断索后双吊索形式自锚式悬索桥安全分析[J]. 大连理工大学学报， 2016， 56（6）： 600-607.

QIU W L， WU G R， ZHANG Z， et al. Safety analysis of self-anchored suspension bridge with dual-shaped hanger after sudden breakage of hanger [J]. Journal of Dalian University of Technology， 2016， 56（6）： 600-607. （in Chinese）

[11] 黄维平， 邬瑞锋， 张前国. 配重不足时的动力试验模型与原型相似关系问题的探讨[J]. 地震工程与工程振动， 1994， 14（4）： 64-71.

HUANG W P， WU R F， ZHANG Q G. Study on the analogy between scale models with less ballast and their prototypes under shaking table test [J]. Earthquake Engineering and Engineering Vibration， 1994， 14（4）： 64-71. （in Chinese）

[12] 项贻强， 吴孙尧， 段元锋. 基于刚度相似原理的斜拉桥模型设计方法[J]. 实验力学， 2010， 25（4）： 438-444.

XIANG Y Q， WU S Y， DUAN Y F. Design method of small-scale cable-stayed bridge based on stiffness similarity theory [J]. Journal of Experimental Mechanics， 2010， 25（4）： 438-444. （in Chinese）

[13] 洪彧， 杨仕力， 刘雨， 等. 桥梁模型试验与新型测试技术2019年度研究进展[J]. 土木与环境工程学报（中英文）， 2020， 42（5）： 1-13.

HONG Y， YANG S L， LIU Y， et al. State-of-the-art review of bridge model test and new testing technology in 2019 [J]. Journal of Civil and Environmental Engineering， 2020， 42（5）： 1-13. （in Chinese）

[14] 柯红军， 李传习. 基于ANSYS的自锚式悬索桥有限元建模和分析方法[J]. 交通与计算机， 2008， 26（5）： 131-135， 138.

KE H J， LI C X. ANSYS-based self-anchored suspension bridge FE modelling and analytic method [J]. Computer and Communications， 2008， 26（5）： 131-135， 138. （in Chinese）

[15] 沈锐利， 房凯， 官快. 单根吊索断裂时自锚式悬索桥强健性分析[J]. 桥梁建设， 2014， 44（6）： 35-39.

SHEN R L， FANG K， GUAN K. Robustness analysis of self-anchored suspension bridge with loss of a single sling [J]. Bridge Construction， 2014， 44（6）： 35-39. （in Chinese）

[16] 郑小博， 张岗， 宋一凡. 双塔钢桁斜拉桥斜拉索破坏动态响应[J]. 长安大学学报（自然科学版）， 2017， 37（6）： 70-77.

ZHENG X B， ZHANG G， SONG Y F. Dynamic response of cable breakage in double-tower cable-stayed bridge with steel truss girder [J]. Journal of Changan University （Natural Science Edition）， 2017， 37（6）： 70-77. （in Chinese）

[17] 公路懸索桥设计规范： JTG/T D65-05—2015 [S]. 北京： 人民交通出版社， 2015.

Specifications for design of highway suspension bridge： JTG/T D65-05-2015 [S]. Beijing： China Communications Press， 2015. （in Chinese）

（编辑 王秀玲）