基于差分隐私的联邦学习数据隐私安全技术*
2022-03-01黄精武
黄精武
(中国电子科技集团公司第七研究所,广东 广州 510310)
0 引言
随着大数据技术日益发展,数据泄露、数据非法访问、数据篡改等数据安全问题越来越受到世界各国的关注,对用户数据的隐私和安全日益严格的管理将是世界趋势[1]。联邦学习(Federated Learning,FL)是一种分布式机器学习策略,通过学习从多个分散的边缘客户端所掌握的训练数据来生成全局模型,有效解决了“数据孤岛”问题[2]。随着联邦学习技术的发展,联邦学习在保护用户训练数据、实现数据“可用不可见”的基础上,获得了性能上较大的提高,并越发接近数据集中式学习的性能[3]。
训练高精度的联邦学习模型需要大规模、高质量的数据支撑,而高质量数据的数据采集、数据清洗和数据标注等预处理工作需要投入高昂的人力、物力,且由于联邦学习中各方数据难以直接获取,联合建模需要多方协调配合,因此联邦学习任务本身需要较高的商业成本。因此,隐私保护是联邦学习系统尤为重要的一个话题。隐私攻击是联邦学习系统面临的一个主要威胁[4],恶意攻击者窃取用户原数据或训练好的模型参数等隐私信息,发起隐私攻击,将会危害联邦学习模型的机密性(Confidentiality)。
联邦学习一经提出,便备受关注。国内外已有大量针对联邦学习中隐私保护技术的性能、安全隐患及其缺点的研究。早在2018年,Rahman[5]便指出了联邦学习中对全局更新贡献较大的参与成员,以及近似推理了原始训练数据。Geiping等人[6]指出了在联邦学习更新过程中,能够从产生的梯度信息近似推理并重构出客户端的原始训练数据。Mothukuri等人[7]在不干涉本地训练过程的前提下,运用成员推断攻击,并通过篡改其在通信过程中传输的梯度,减弱了全局模型的效能。
本文主要针对联邦学习可能面临的安全和隐私威胁进行分析,着重阐述隐私安全问题,总结了一些防御措施。在这些防御措施中,本文重点对差分隐私进行介绍,分析其隐私安全性能,以期进一步减小联邦学习系统中的隐私风险。此外,还利用基于拉普拉斯机制[8]的差分隐私算法设计了一个联邦学习的隐私保护方法,并通过实验分析了该方法对模型性能的影响。
1 联邦学习概述
联邦学习是一种分布式机器学习算法,但在学习过程中,各个参与方不会共享自身的训练数据,每个联邦学习利用多个计算节点进行联合训练,旨在提高性能、保护隐私信息,并使其可以扩展到更大规模的训练数据和更大规模的模型[9]。联邦学习打破了“数据孤岛”,实现了数据隐私保护和共享分析的平衡,即“数据可用不可见”的数据应用模式。
1.1 联邦学习的定义
联邦学习中的角色主要包括客户端(参与方)和服务器。假设有k个客户端参与了联邦学习,第i个客户端为Ci,所拥有的训练数据集为Di,本地模型为Mi,其中i=1,2,3,…,k。联邦学习的目标是从所有训练数据组成的数据集中训练出一个全局模型MGlobal。目前联邦学习系统中常用的聚合策略包括联邦平均(Federated Averaging,FedAvg)和联邦随机梯度下降(Federated Stochastic Gradient Descent,FedSGD)等。然而,不同于直接利用数据集D本身来训练一个中心化模型MCentral,在联邦学习中,第i个客户端不能访问数据集假设模型的效果为V,则联邦学习系统的优化目标为:
式中:||·||为某种范数或距离度量。
一般地,基本的联邦学习系统至少包括初始化(分发全局模型)、本地更新和全局聚合3个步骤。[10]
1.2 联邦学习的分类
联邦学习系统中,每个参与方Ci只拥有其本地的训练数据集Di,并且这些数据集在样本空间和特征空间上有不同程度的重合,造成了联邦学习系统进行学习的依据不同。根据学习依据,联邦学习系统分为横向联邦学习、纵向联邦学习和联邦迁移学习3类。
横向联邦学习按照样本空间对数据集进行划分,并取出特征相同而样本不同的部分来进行训练。纵向联邦学习与横向联邦学习相反,是根据特征分布来进行学习的。联邦迁移学习适用于参与方的数据集中特征空间和样本空间重叠都很少的情况。联邦迁移学习中,不对数据进行切分,而是利用迁移学习[11]的方法来解决数据及标签不足的问题。
2 联邦学习面临的隐私威胁
尽管联邦学习系统中各个参与方的训练过程是独立进行的,且没有原始训练数据的传输,可以保证一定的隐私安全,但这并非绝对安全的。恶意的参与方可以从更新信息中推理出较为活跃的成员信息,甚至可以重构训练数据。
2.1 联邦学习中的隐私威胁
联邦学习中的参与方往往容易受到模型提取攻击[12]和模型逆向攻击[13]这两大类攻击。联邦学习系统中一般假定服务器端是非恶意的,但这样的假设不能防范“诚实但好奇”(Honest but Curious)[6]的服务器,这类服务器端虽然确实完成了应有的聚合任务,不会对模型性能发起攻击造成破坏,也不会破坏模型的可用性,但是会尝试窃取参与方本地数据集中的数据,破坏参与方数据的机密性,威胁数据参与方的隐私安全。
2.2 模型提取攻击
在模型提取攻击中,攻击者试图窃取模型的参数、超参数等,破坏了模型的机密性。
一般而言,模型提取攻击中,攻击者试图构建一个与原模型相似的替代模型。因为攻击者缺少对模型结构的了解,所以此类攻击一般为黑盒攻击。首先,攻击者利用一组数据X={X1,X2,…,Xn}对被提取的模型发起查询操作,并获得查询结果Y={Y1,Y2,…,Yn},由此构造出一个训练数据集D={(X1,Y1),(X2,Y2),…,(Xn,Yn)};其次,攻击者将利用数据集D来训练替代模型,直到替代模型的效果达到了攻击者的预期。模型提取攻击的基本原理如图1所示。
在实际应用过程中,联邦学习模型的训练代价与成本都是较高的,而模型提取攻击使得攻击者能够以极低的训练代价获得一个与原始模型性能相近的替代模型,严重损害了联邦学习参与方的隐私安全和商业利益。
2.1.2 模型逆向攻击
在模型逆向攻击中,攻击者一般试图通过在训练完毕的模型中不断地查询,获得一些统计信息,进而推理出用户的隐私信息。根据攻击者推理的信息,可以将模型逆向攻击分为属性推理攻击(Property Inference Attack,PIA)[14]和成员推理攻击(Member Inference Attack,MIA)[15]。在属性推理攻击中,攻击者的目标在于判断参与方的训练数据集中是否含有某个特征。在成员推理攻击中,攻击者的目标在于判断某一条数据记录是否包含在参与方的训练数据集中。
除上述推理攻击,近几年一些基于生成对抗网络(Generate Adversarial Networ,GAN)的推理攻击[16]也成为一种较常见的逆向攻击的手段。
3 防御隐私威胁的措施
联邦学习的隐私防护工作需要从参与方和服务器两大主体分别进行。从原理上来看,多数联邦学习隐私安全的方法都是基于密码学的。
基于密码学的联邦学习隐私安全方法主要包括安全多方计算[17]、同态加密[18]等,主要用于模型训练阶段的隐私保护,可以防御一些模型逆向攻击。这些方法可以用来防御恶意的或“诚实但好奇”的参与方和服务器端,且在传输信息被截获的条件下,仍然能从密码方面保障安全。这些保护措施的安全性主要体现在密码学算法的安全性,同时需考虑密码学算法的时空效率。
另外有一些不基于密码学的隐私安全方法,例如差分隐私(Differential Privacy,DP)[19],主要用于模型训练完毕后的隐私保护,其可以通过加噪的方法防御一些模型提取攻击和推理攻击。这些保护措施的安全性的高低主要体现在能否使得明文信息能够推理出尽量少的敏感信息。
4 差分隐私方法概述
4.1 差分隐私的基本定义
在介绍差分隐私的定义之前,首先介绍邻近数据集(Adjacent Dataset)的定义。设有两个数据集D与D',若它们的对称差中元素的数量满足|DΔD'|=1,则称D与D'互为邻近数据集。
差分隐私在提出的初期,主要应用于数据库安全保护。设f为一个查询函数,即一个映射,可以是求和、求平均、求最值或其他查询操作,则攻击者多试图通过比较f(D)与f(D')的差异来推理出数据库中的敏感信息。一个推理攻击的示例如图2所示。
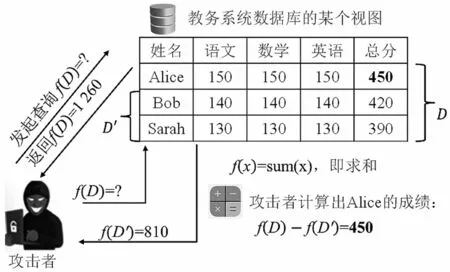
图2 推理攻击示例
对于邻近数据集D与D',设有一随机算法M,PM为该算法所有可能的输出,对于任意SM⊂PM,都有:
则称随机算法M满足∊-差分隐私。式中:e为自然对数的底数;∊为隐私预算。当隐私预算∊的值越小,随机算法M在D和D´上获得相同的输出结果的概率也就越接近,所以当用户对数据集进行查询的时候,无法通过输出结果区分这条数据是来自邻近数据集中的D还是D',即无法察觉到这个数据集中微小的变化。反之,∊的值越大,隐私保护效果也就越弱。因此,可以得出,过大的隐私预算会导致无法达到预期的隐私保护效果,过小的隐私预算虽然能达到隐私效果,但加噪力度太大容易导致查询结果完全无法使用。
若随机算法对于D与D'满足:
其中,δ>0,则称随机算法M满足(∊,δ)-差分隐私。δ是一个松弛项,表示差分隐私可以接受一定程度的不满足。
4.2 差分隐私的敏感度分析
为了获知对于特定的随机算法函数M,需要添加多少噪声才能满足(∊,δ)-差分隐私,并且需要获知该算法在当前数据集中删除一条数据引起的查询结果的最大改变量。差分隐私算法有两种敏感度,分别是全局敏Gt感度(Global Sensitivity)和局部敏感度(Local Sensitivity)。
4.2.1 全局敏感度
设一映射f:D→Rd,其输出为d维实向量,则全局敏感度定义如下:
全局敏感度为一个l1范数定义的表达式,由函数本身决定,而和D与D'无关。当全局敏感度较小时,只需要添加较小的噪声,就能使函数M满足(∊,δ)-差分隐私。
4.2.2 局部敏感度
由于全局敏感度较大时,需要添加强度足够大的噪声才能保证隐私安全,这可能导致数据不可用,因此Nissim等人定义了局部敏感度,则f在数据集D上的局部敏感度具体为:
可以发现局部敏感度与全局敏感度的关系如下:
局部敏感度通常比全局敏感度要小很多,并且局部敏感度取决于映射f本身与原始数据集D,然而,局部敏感度在一定程度上体现了数据集的分布特征,因此只用局部敏感度来确定噪声强度大小,仍然容易造成隐私泄露。
4.3 差分隐私的实现方法
在具体实现差分隐私时,需要根据不同的随机算法采取不同的实现机制。常见的机制包括指数机制(Exponential Mechanism)和拉普拉斯机制(Laplace Mechanism)等。
4.3.1 拉普拉斯机制
拉普拉斯机制是向确定的查询结果中加入服从拉普拉斯分布的噪声。此分布有两个参数,包括尺度参数λ和位置参数μ,其分布密度函数为:
将该分布记作Lap(μ,λ)。如向查询结果中添加尺度参数的服从拉普拉斯分布的噪声n能够形成一个随机算法M,即M(D)=f(D)+n,则可以证明随机算法M提供了∊-差分隐私保护[8]。其中,Δf指的是f的敏感度。
一般来说,拉普拉斯机制适合数值型结果的保护。
4.3.2 指数机制
在许多应用场合,查询结果都是非数值的,例如一个实体对象。设r为随机算法的输出,q(D,r)为一个用来评估输出优劣性的可用性函数,Δq为q(D,r)的敏感度。可以证明[20],如随机算法M能够以正比于的概率输出r,则算法M能够提供∊-差分隐私保护。
5 利用差分隐私保护联邦学习系统安全
在安全保护领域的隐私保护机器学习(Privacy-Preserving Machine Learning,PPML)技术中,主要有两种攻击者:一种是“诚实但好奇”的攻击者,这种攻击者会诚实地遵守协议,但会试图从接收到的信息中获取更多输出结果以外的信息内容;另一种是恶意的攻击者,这种攻击者不遵守规定的协议,会试图发起任意的攻击行为。本文采用拉普拉斯机制来实现差分隐私,提出了一种差分隐私方法,并简要分析了方法的合理性。
5.1 联邦学习服务器对隐私安全的保障
为了满足以上隐私保护的目的和要求,本文在协调方发送给各个参与方的全局模型上实施差分隐私保护。在本文的联邦学习系统中,聚合算法采用联邦平均算法,其表达式为:
式中:t为全局模型更新的轮次;G t和G t+1为第t轮次和第t+1轮次更新的全局模型参数;η为全局模型更新λ的学习率;n为客户端的数量;m为当轮被选择参与本轮全局模型更新的客户端数量;为在第t+1迭代轮次中被选中的第i个参与方在本地数据训练后的本地模型;为第t+1迭代轮次中被选中的第i个参与方在本地数据训练的更新梯度。
因此,当“诚实但好奇”的参与方或是恶意的参与方对模型发起成员推理攻击,威胁参与方隐私安全和数据安全时,所要查询的就是协调方发送给各个参与方的全局更新模型G t+1,所以可以得知查询函数为:
为了防止服务器发出的全局更新被攻击者推理出敏感信息,服务器将在聚合时对模型梯度添加噪声。这里采用的是拉普拉斯机制。服务器端的聚合方法如下:

其中,查询函数敏感度的一个边界为:
式中:M'为参与方集合M的用户邻近数据集,即集合M'与集合M相比,有且仅有一个参与方不同;||Δk||1为第k个参与方更新梯度的l1范数。
式(11)中,当||Δk||1≤C时,式子中的分母会取到1,裁剪出来的梯度Δ与裁剪前的梯度Δk相同,满足裁剪边界||Δk||1≤C;当||Δk||1≥C时,分母的值会取到,于是裁剪后的度的值就为,也同样满足裁剪边界||Δk||1≤C,因此,该裁剪方法是合理的。
5.2 联邦学习参与方对隐私安全的保障
对于一个非恶意的服务器而言,如4.1节所述,其隐私保护的主要目的是防御恶意的参与方或外部攻击者实施推理攻击。同样地,作为一个联邦学习参与方,也需要防范一些非善意的参与方或服务器试图破坏隐私安全的行为。因此,参与方在上传其梯度更新时,也将对梯度进行一些诸如梯度裁剪的处理,以保护其隐私安全。
对于参与方而言,通过对裁剪梯度,可以做到本地差分隐私(Local Differential Privacy,LDP)[19]。在这种方式之下,参与方对自己上传至协调方的梯度进行扰动,对梯度进行裁剪再上传至协调方可以在协调方不受到信任的时候能够有效地对本地数据进行保护,将已混淆的数据发布至不受信任的协调方可以有效地保护参与方用户的隐私安全和数据安全。同样地,据3.3节所述,下列算法能够做到(∊,δ)-差分隐私。
参与方所完成的任务是训练本地模型并上传更新梯度,上传更新的算法如下:

5.3 实验分析
据5.1节与5.2节所述,算法1和算法2在理论上能够做到差分隐私。下文将分析差分隐私对联邦学习性能的影响度,这里采用的实验数据集为CIFAR-10,采用的图片分类模型为卷积神经网络(Convolutional Neural Network,CNN)的ResNet-18网络结构。
5.3.1 收敛效率与准确率分析
本节分别对比了联邦聚合算法FedAvg和FedSGD在加入差分隐私前后的性能。将联邦平均算法FedAvg的参数设置为:全局模型迭代轮次(epochs)E=100,参与方总数N=10,每轮选择参与训练的参与方数量n=3,参与训练的用户方本地训练轮次e=3。联邦梯度下降算法FedSGD参数设置为:全局模型迭代轮次E=100,参与方总人数N=10,每轮选择参与训练的参与用户数量n=10,参与训练的用户方本地训练轮次e=1。基于拉普拉斯噪声的差分隐私算法的参数设置为:拉普拉斯噪声的标准差σ=0.001,参与方上传的梯度的裁剪阈值c=1。
实验结果如图3所示。由图3可知,图中所示训练方法的模型准确率都随训练轮次的增加而逐渐增加,最后都稳定在75%左右,且两种聚合算法FedAvg和FedSGD的收敛速度和准确率无明显区别。同时发现,添加了差分隐私的两种联邦平均算法与不添加差分隐私的原始算法的收敛速度与准确率也无明显差距。这说明,差分隐私一般不会显著影响模型的收敛性能。
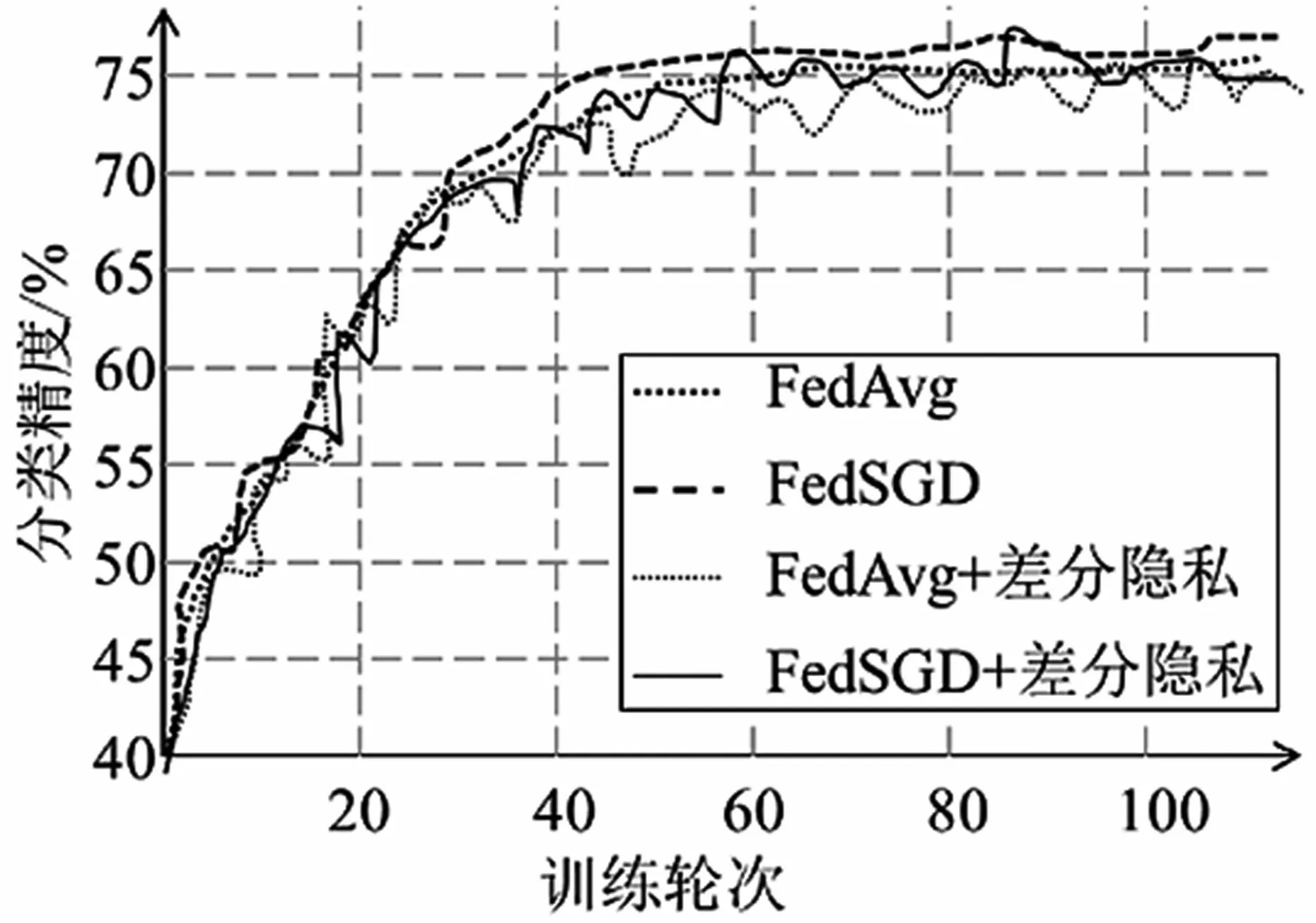
图3 联邦聚合算法FedAvg和FedSGD在加入差分隐私前后的性能对比
5.3.2 差分隐私参数的变化影响分析
本节分析的参数是隐私预算,这里通过调整拉普拉斯噪声的标准差σ来控制隐私预算,所用的聚合算法是FedAvg,其参数设置为:全局模型迭代轮次E=100,参与方总数N=10,每轮选择参与训练的参与用户数量n=3,参与训练的用户方本地训练轮次e=3,参与方上传的梯度的裁剪阈值c=1。对添加拉普拉斯噪声的大小按一定间距设置,并进行对比。
实验结果如图4所示。从图中可以看出,在同样的迭代轮次中,随着添加的拉普拉斯噪声标准差逐渐增大,即随着隐私预算的减小,训练模型的准确率有明显的降低。若要使联邦学习训练模型达到同样的准确率和性能大小,需要训练更多的轮次才可达到这样的效果。结合图3可以发现,虽然差分隐私措施对于模型的收敛性可能无显著影响,但收敛后的最优效果可能随着隐私预算的减小而出现显著损失。
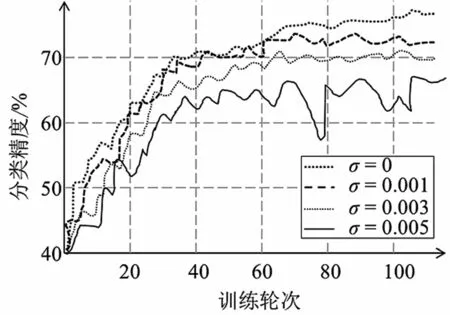
图4 添加的拉普拉斯噪声的大小对联邦学习模型准确率的影响
5.3.3 裁剪阈值的变化影响分析
本节对裁剪阈值的变化进行分析,所用的聚合算法是FedAvg,其参数设置为:全局模型迭代轮次E=100,参与方总人数N=10,每轮选择参与训练的参与用户数量n=3,参与训练的用户方本地训练轮次e=3,模型添加的噪声σ=0.001。对用户上传梯度的裁剪阈值按一定间距设置,并进行对比。
实验结果如图5所示。可以发现,不同参与方上传的梯度裁剪阈值下的曲线几乎重合,即参与方上传的梯度裁剪的阈值的不同对模型的性能无显著影响,即不会显著影响模型训练的准确率和模型收敛性。

图5 裁剪参与方上传梯度的阈值对联邦学习模型准确率的影响
综上实验结果分析表明,这里提出的差分隐私算法,除了在理论上能够保证差分隐私,也不会对被保护模型的收敛性能有显著影响。然而,拉普拉斯噪声的添加会导致模型准确率的下降,且随着噪声标准差的增大,模型准确率的下降愈发剧烈。此外,梯度裁剪方法不会对模型准确率产生显著的影响,这是因为梯度裁剪算法并没有向梯度信息中添加噪声。在简单模型和数据集上,差分隐私算法的添加也不因聚合算法的不同而显著影响模型的收敛性能和准确率。因此,可以得出,上述的联邦学习差分隐私算法在不显著影响模型准确率的前提下能实现隐私保护。
6 结语
本文主要研究了差分隐私在联邦学习隐私保护中的一些应用,探讨了差分隐私的不同实现机制及其适用条件。最后本文讨论了差分隐私对联邦学习系统中不同角色的应用方法,简要分析了具体算法,并得出联邦学习中差分隐私方法能够在不显著影响模型准确率的前提下实现隐私保护。
此外,联邦学习本身虽然有一定的隐私保护属性,但仍存在一定的隐私风险。在联邦学习系统中,差分隐私方法中裁剪的阈值和噪声的大小决定着对参与方本地数据隐私和用户隐私的保护强度,裁剪阈值越小则对本地数据隐私保护的强度越强,噪声大小越大则对用户隐私的保护强度越强。
