基于瞬时特征谱的联合特征调制识别算法*

罗 强，刘一兵，赵 洋

（中国人民解放军63892部队，河南 洛阳 471003）

0 引言

在通信侦察对抗、无线频谱监测、信号认知认证等非协作通信[1]的应用中，调制识别作为其中的关键环节，通过对多维度的信号特征进行联合分析来判别信号的调制方式，为信号参数分析、信息监控、对抗干扰等环节提供重要支撑。

针对信号的调制识别方法主要包括基于判决理论识别和基于统计模式识别两种方法[2-4]。判决理论识别方法属于非参数方法，从本质上可看作在无穷维的信号空间上，基于不同信号在空间上的概率分布差异，通过广义似然比等判决准则[5-6]对信号进行分类的过程。实际分析中，信号采样后由无穷维变为有限维，但高维的贝叶斯估计或者K近邻等决策算法仍然需要巨量的样本才能拟合出信号的空间分布，因而该方法应用较少。统计模式识别主要通过提取与调制方式相关的识别特征，将信号空间映射到能代表信号模式的特征空间，并通过特征空间的差异来区分信号模式。统计模式识别方法降低了空间维度，便于工程实现，但识别效果与特征的选取高度相关。目前，统计模式识别方法选取的特征通常包括瞬时特征、高阶累积量特征、循环谱特征、小波特征、分形特征[7]、星座图特征[8-10]等。这些特征在特定条件下均能对调制类型进行有效识别，但识别效果受限于信号的信噪比、成型脉冲形状、采样率，同时部分特征的计算量制约了算法的工程应用。

本文在信号瞬时特征的基础上进行特征变换，将高阶调制映射为低阶调制，基于变换后谱密度的功率变化和分布变化，同时结合瞬时特征统计量、谱相关特征、分形特征，对2ASK、4ASK、2FSK、4FSK、BPSK、QPSK这6种数字调制信号进行识别分类，并通过集成学习模型进行分类，有效提升了低信噪比环境下信号识别的正确率。

1 瞬时特征谱

典型的瞬时特征方法通过对信号的瞬时幅度、频率、相位进行归一化，提取其标准差、峰度等信息来区分信号的调制类型。这些特征包括绝对幅度、相位和频率标准偏差，均值归一化包络方差参量，信号包络峰度，频率峰度等，属于二阶统计量，对噪声以及脉冲成型滤波非常敏感[11]。为了提升识别算法对成型滤波的适应能力，可基于统计量的频域来设计特征。

瞬时特征谱的基本思想是，信号瞬时特征以符号宽度为周期进行规律变化，对瞬时特征求功率谱密度，谱密度会集中在符号带宽内，通过对瞬时特征进行不同的数值变换，其功率谱密度会发生不同变化，从而区分出不同阶数的数字调制。

接收端信号r(t)满足模型：

式中：A(t)为已调信号振幅；θ(t)为已调信号相位；n(t)为窄带高斯噪声；wc为信号载频。信号的包络、相位形式如下：

式中：z(t)，φ(t)分别为接收信号的包络和相位。

信号经正交下变频后的基带形式为：

信号的瞬时幅度、瞬时相位、瞬时频率分别为：

定义信号的N阶瞬时特征如下：

式中：Inst为InstA(t)、InstP(t)、InstF(t)的缩写形式。

信号的N阶瞬时特征谱为：

式中：RN(τ)为InstN的自相关函数。

理想的2N阶ASK/PSK/FSK调制信号所对应的瞬时幅度/瞬时相位/瞬时频率，其N-1阶瞬时特征的均值为二值函数，N阶瞬时特征均值为0。N-1阶瞬时特征的谱密度主要集中在符号速率Rb对应的频率范围内，N阶瞬时特征的谱密度则为白噪声。以4阶调制的瞬时特征谱为例，如图1、图2、图3所示，一阶瞬时特征谱相比0阶瞬时特征谱，总功率明显降低，并且低频分量的功率比高频分量的功率下降更快，高斯白噪声二阶瞬时特征谱已趋近于白噪声。

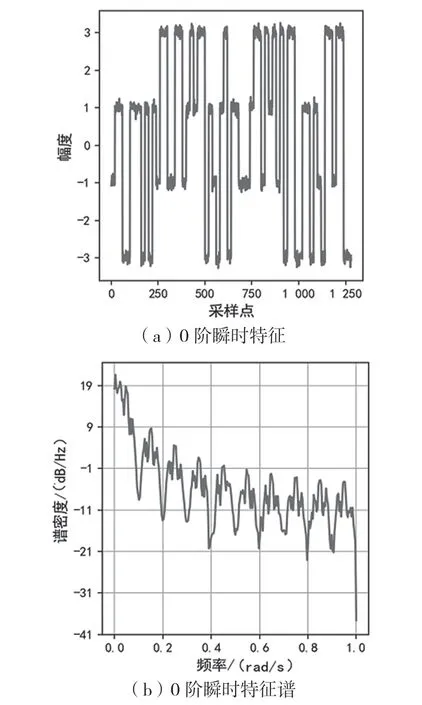
图1 4阶调制的0阶瞬时特征谱

图2 4阶调制的1阶瞬时特征谱

图3 4阶调制的2阶瞬时特征谱

考虑基于Rb范围内瞬时特征的功率变化以及总体谱密度的分布变化来区分数字调制阶数。定义信号的N阶瞬时特征谱增量ΔPN，以及N阶瞬时特征谱熵增量ΔSN(q)，则有：

式中：pN(q)为N阶特征谱中，频率q以下的功率占比；SN(q)为该分布在q频率分位处的分布度量。

信号的瞬时特征谱增量、谱熵增量分别从功率变化、分布改变的角度对变换后瞬时特征的功率谱进行度量。脉冲成型以及各类滤波会改变信号的瞬时特征谱，但不会改变瞬时特征谱随着阶数改变的变化趋势，这也体现为特征在一定信噪比范围内对信号失真不敏感。

2 瞬时特征谱的抗噪声性能

以2ASK、4ASK、BPSK、QPSK、2FSK、4FSK为数据集，通过仿真实验研究瞬时特征谱增量、谱熵增量随信噪比的变化情况，分析其识别性能。实验数据为零中频IQ信号，符号速率Rb=10 000 Baud，采样频率fs=100 kHz，ASK、PSK成型函数为升余弦滚降脉冲，滚降系数为0.5，FSK信号调制指数为1，仿真数据长度为512个符号，信噪比范围为0～20 dB。

图4、图5、图6依次为信号的瞬时幅度谱、相位谱、频率谱的增量与信噪比的变化关系曲线。从图4可以看出，一阶幅度谱增量可以将2ASK与4ASK区分开来，二阶幅度谱增量能在一定信噪比范围内将ASK与其他调制区分开。从图5可以看出，相位谱增量的标准差较大，区分能力有限。从图6中可以看出，瞬时频率谱增量能在较低信噪比水平下将2FSK与4FSK区分开。

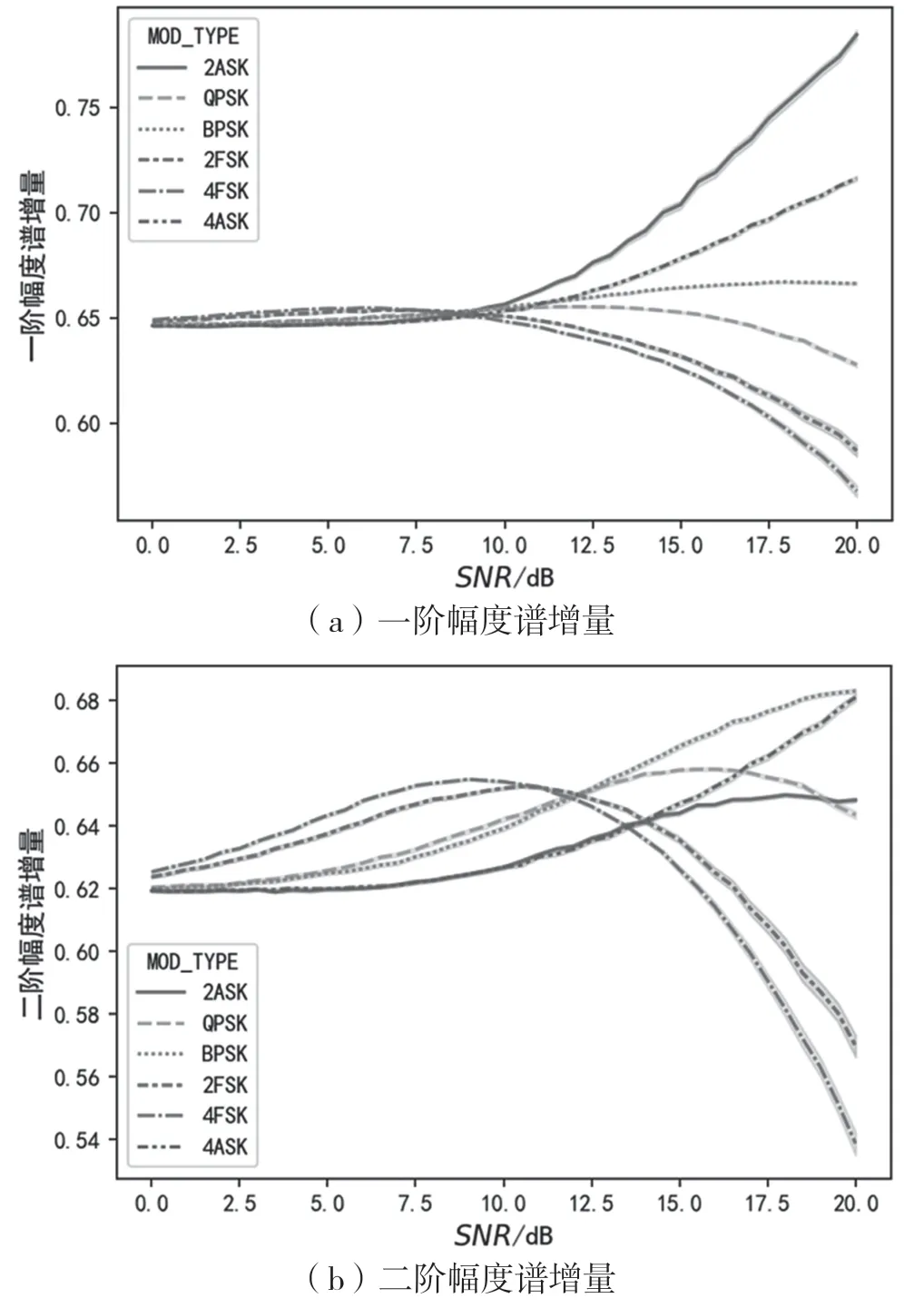
图4 一阶、二阶幅度谱增量

图5 一阶、二阶相位谱增量

图6 一阶、二阶频率谱增量

图7、图8、图9依次为一阶、二阶的瞬时幅度谱、相位谱、频率谱的谱熵增量（q=0.5Rb）与信噪比的变化关系曲线。从图7中可以看出，一阶幅度谱熵增量可以在0～20 dB的信噪比范围内，将ASK、PSK、FSK明显区分开来，二阶幅度谱熵增量能在固定的信噪比上将2ASK、4ASK、BPSK区分开，但在信噪比未知的情况下区分能力有限。从图8中可以看出，相位谱熵增量能在较低信噪比水平下将BPSK与QPSK区分开，二阶相位谱熵增量比一阶相位谱熵增量的标准差更小。从图9中可以看出，一阶瞬时频率谱熵增量能明显将FSK与其他调制区分开，二阶瞬时频率谱熵增量能明显将2FSK与4FSK区分开。

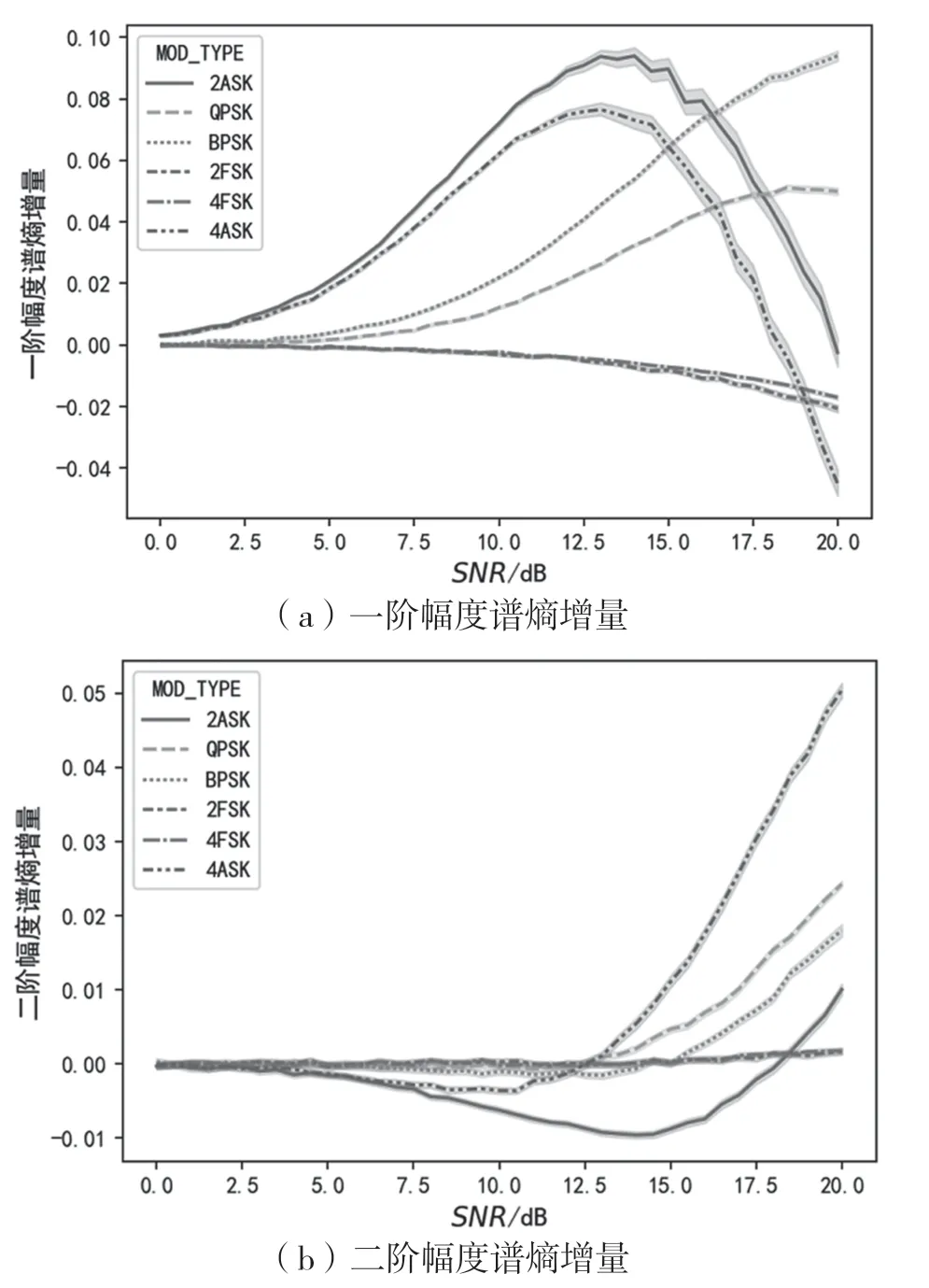
图7 一阶、二阶幅度谱熵增量

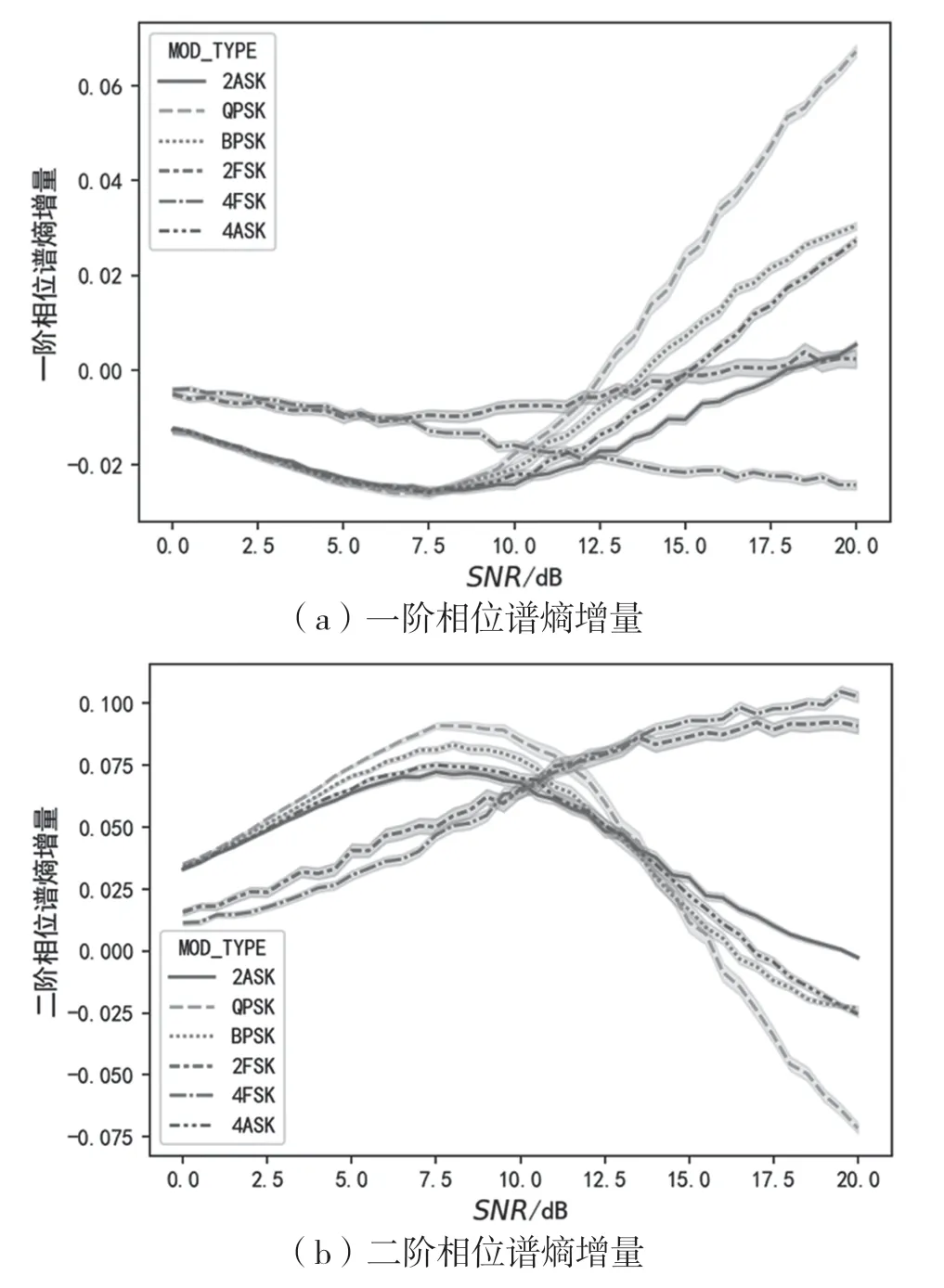
图8 一阶、二阶相位谱熵增量

图9 一阶、二阶频率谱熵增量

总体而言，瞬时特征谱增量和瞬时特征谱熵增量对不同的信号均有一定的区分能力，但单独一个特征无法对不同信噪比的不同信号进行有效区分，因此需要将特征进行组合，构造特征空间下的类别分布，通过不同模型的分类器对信号进行识别。

3 分类器的设计及仿真

构造的特征空间通常是非线性的，使用线性分类器无法对空间进行有效区分，因此本文使用树形结构分类器。当样本数量规模较大时，树形分类器通过空间搜索，能使特征参数在高维空间有效地收敛到不同的信号类别。在此，利用boosting算法中的残差提升模型XGBoost，将多个弱学习器进行集成，实现特征空间到类别空间端到端的学习分类。

XGBoost将损失函数展开至泰勒二阶函数，并引入正则化项，其损失函数为：

式中：L(t)为第t棵树的损失函数；为第t棵树之前的树的损失值；gi为关于第t棵树之前预测值的一阶导数；hi为关于第t棵树之前预测值的二阶导数；ft(xi)为需要求解的第t棵树；Ω为对树的数量的惩罚项。XGBoost算法最大的优势在于性能，无论是从准确率还是计算速度，相比于SVM、神经网络等经典算法，更具有实效性[12]。

选择待识别的信号集为2ASK、4ASK、BPSK、QPSK、2FSK、4FSK共6种数字调制信号。符号速率Rb=10 kBd，采样频率fs的范围为50～200 kHz，符号个数为128～1 024，ASK、PSK成型函数为升余弦滚降脉冲，滚降系数为0.3～0.7，成型滤波长度为6～20倍的Rb[13]，FSK信号调制指数为0.6～2，信噪比定义为信号带宽内的信号噪声能量比，范围为0～20 dB，信号相位为随机相位。信号样本集为100 000个，训练集为80 000个，测试集为20 000个。

信号集所需的瞬时特征谱阶数为2阶，提取信号的6个瞬时特征谱增量，选取q=[0.5Rb,Rb]，提取信号的12个瞬时特征谱熵增量。采用XGBoost学习器，树个数设置为100个，深度设置为10层。提取8个传统瞬时特征参量[14]、2个谱相关特征参量、2个分形特征[15]参量作为基本特征，然后单独使用瞬时特征谱特征，最后将瞬时特征谱特征与基本特征进行联合，通过学习训练，对不同特征组合下的信号进行调制识别，识别正确率的结果如图10所示。

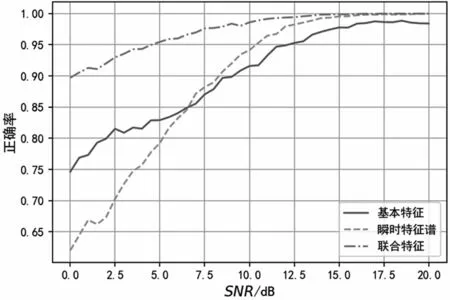
图10 分类识别正确率

可以看出，当SNR＜6 dB时，基本特征的识别效果要优于瞬时特征谱，这是因为基本特征涉及多个维度的设计，单一维度下设计的特征很难在所有信噪比下优于多个维度特征的识别效果；当SNR＞6 dB时，瞬时特征谱的识别效果要优于基本特征且提升明显。特征联合后，基本特征的识别正确率大幅提高，当SNR＞8 dB时，联合特征的识别正确率接近100%。

当10 dB＜SNR＜20 dB时，基本特征识别的平均正确率为98.3%，瞬时特征谱识别的平均正确率为99.5%，联合特征的识别正确率为100%。不同特征识别的混淆矩阵如图11、图12和图13所示。对比混淆图可知，基于瞬时特征谱的识别效果在4ASK、QPSK的识别正确率比基本特征要高7%和3%，基本特征的4ASK、QPSK存在相互误判的情况，这是因为线性调制中，为了控制信号带宽，对基带脉冲做了成型处理，导致基本特征中的统计特性对信号的区分能力变弱。

图11 基本特征识别混淆矩阵（10 dB＜SNR＜20 dB）

图12 瞬时特征谱识别混淆矩阵（10 dB＜SNR＜20 dB）

图13 联合特征识别混淆矩阵（10 dB＜SNR＜20 dB）

当0 dB＜SNR＜10 dB时，基本特征识别的平均正确率为92.8%，瞬时特征谱识别的平均正确率为91.7%，联合特征的识别正确率为98.7%。不同特征识别的混淆矩阵如图14、图15和图16所示。对比混淆图可知，基于瞬时特征谱的识别效果在4ASK、QPSK的识别正确率比基本特征要高20%和7%，其他特征的正确率要低于基本特征，特征联合后，正确率显著提升。

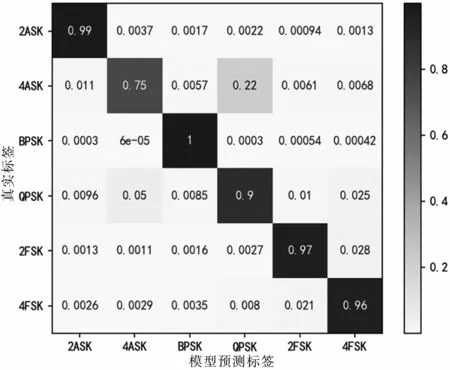
图14 基本特征识别混淆矩阵（0 dB＜SNR＜10 dB）

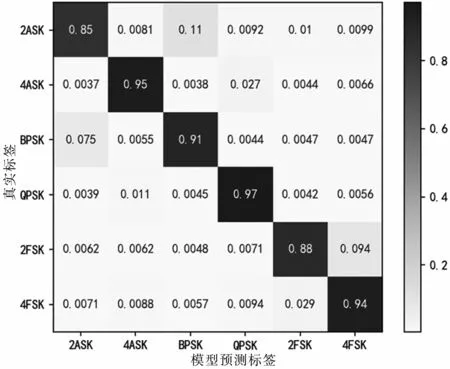
图15 瞬时特征谱识别混淆矩阵（0 dB＜SNR＜10 dB）

图16 瞬时特征谱识别混淆矩阵（0 dB＜SNR＜10 dB）

实际信号分析中，对信号的载频估计往往存在一定偏差，因此对信号集的基带信号加入一定频偏，频偏范围在±fs/100之间，信号识别的正确率如图17所示。可以看出，当SNR＞3 dB时，瞬时特征谱的性能要优于基本特征，且正确率随信噪比的增加快速提升，而特征联合后，正确率要远高于基本特征，这也体现了瞬时特征谱算法对先验信息的不敏感。

图17 分类识别正确率（加入频偏）

4 结语

本文提出了一种基于瞬时特征谱的特征构建方法。该方法首先对信号的瞬时特征进行多阶变换，其次从谱功率和谱分布两个维度进行特征设计，最后以XGBoost集成学习器分类器进行调制识别。仿真结果显示了基于瞬时特征谱信号识别方法的有效性，在低信噪比情况下能大幅提升传统特征参数识别的正确率，因此具有一定的实用价值。