可见光ACO-OFDM系统信道估计算法研究*

张 振，李永伟

（中电科普天科技股份有限公司，广东 广州 510310）

0 引言

科研结果显示，室内发光二极管（Light Emitting Diode，LED）光源在非视距链路（Non Line of Sight，NLOS）下，地面的接收器在模拟空间边缘位置接收到的信号呈现稀疏特征，严重影响了系统的通信性能。

信道估计是提高通信性能的方法之一，其原理是计算得到该信道模型的相关参数及信道模型的冲激响应，使系统能够适应该信道模型，提高通信的性能。研究结果显示，非对称限幅光正交频分复用(Asymmetrically Clipped Optical Orthogonal Frequency Division Multiplexing，ACO-OFDM）系统仅使用奇载波传递数据，而最小二乘算法和最小均方误差算法这些比较传统的信道估计算法，并不适用于子载波资源较为紧缺的ACO-OFDM系统，原因是上述两种算法的实现需要占用大量的导频资源，才能准确地估计出信道的模型。现有多项研究显示，为适应ACO-OFDM系统子载波数目较少的特征，压缩感知（Compressed Sensing，CS）技术[1]是一个很好的选择。

压缩感知技术是利用信号呈现出来的稀疏特性，通过基于压缩感知的信号重构算法，实现信号的完美重建[2]。现阶段应用较为普遍的基于压缩感知的信号重构算法主要有正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法[3]、稀疏度自适应匹配追踪（Sparsity Adaptive Matching Pursuit，SAMP）算法[4]、多路径匹配追踪广度优先（Multipath Matching Pursuit-Breadth First，MMP-BF）算法[5]。

基于压缩感知的稀疏信号重构算法的实现需要把恢复矩阵作为先决的条件。研究表明，恢复矩阵的互相关性越小，信号的恢复质量越高[6]，而恢复矩阵的互相关性与系统的导频位置密切相关，可以说导频位置的选择决定着恢复矩阵的互相关性，所以导频位置的优化选择是极其重要的。传统的导频优化算法中，如穷举法和随机序列搜索算法（Stochastic Search Schemes，SSS）的实现需要较长的计算时间，对计算服务器有着较高的要求，并且容易陷入求解局部最优化的问题，影响计算结果的准确性。相较于传统的导频优化算法，文献[7]在OFDM系统中利用树状随机导频搜索（Tree-based Stochastic Search，TSS）算法进行导频优化设计，运用多个搜索分支的迭代运算，并采用正交匹配追踪（Orthogonal Matching Pursuit,OMP）算法进行信道估计，有效降低了通信系统的误码率。

本文首先运用压缩感知技术对稀疏信号进行稀疏表示；其次将ACO-OFDM系统的特征与压缩感知技术相结合，并将信道估计技术同基于压缩感知技术的稀疏信号重构算法相结合；再次对导频优化TSS算法进行描述；最后将TSS算法同压缩感知算法相结合，运用到ACO-OFDM系统信道估计技术中，经过仿真实验，得到仿真数据。

1 压缩感知与信道建模

1.1 压缩感知稀疏信号表示

假设原始信号v为N×1维，并且能够找到一组N×N维正交基ψ=(ψ1,ψ2,…,ψn)，通过N×1维加权系数向量h来线性表示v，则原始信号v可表示为：

利用压缩感知技术进行数据压缩，即用与正交基不相关的M×N维的矩阵Φ去压缩原始信号v，得到M×1维信号y，Φ为观测矩阵，可得：

将式（2）展开写成：

式中：T为恢复矩阵[8]。

1.2 NLOS下稀疏信道模型

如图1所示为室内可见光通信链路，将LED抽象成一个点发射源S，S可表示为S=(rs,Vs,m)，rs和Vs分别为S的位置向量和单位法向量，其中rs=(Xs,Ys,Zs)。

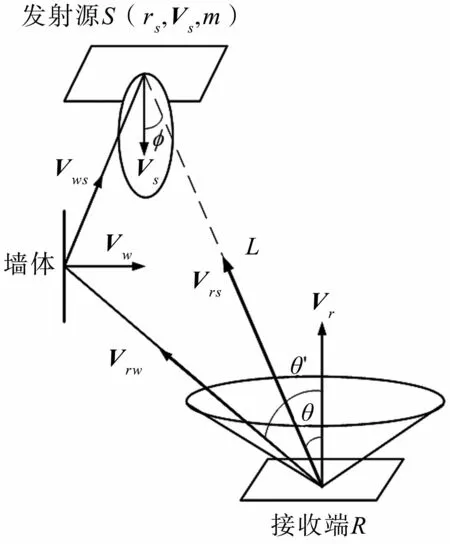
图1 室内可见光通信链路

1.3 压缩感知技术的应用模型

经研究显示，ACO-OFDM系统仅使用奇载波传播数据，这也是ACO-OFDM技术特性之一，所以只能用ACO-OFDM系统奇载波数据作为导频数据，以便开展更准确的信道估计。现将P个子载波数据作为导频数据，其可表达为[9]：

式中：(·)*表示共轭。

现将P个子载波作为导频信号，其在ACOOFDM系统中的位置索引可表示为n={n1,n2,…,np}，则对应发送的数据可记作X(n1),X(n2),…,X(np)，接收端接收的数据可记作Y(n1),Y(n2),…,Y(np)。定义W为P×L维快速傅里叶变换矩阵，H=(H1,H2,…,HL)T为信道时域脉冲响应，V为高斯白噪声记作V1,其中，快速傅里叶变换矩阵是比较常见的观测矩阵。

ACO-OFDM系统接收到的导频信号为：

将式（5）写成向量形式，可表示为：

式中：A为频域信号映射后的时域信号。

这样将ACO-OFDM信道估计问题转变为压缩感知的信号重构问题。

2 TSS导频优化算法

本文采用复杂度较低的互不相关特性准则（Mutual Incoherence Property，MIP）[7]当作恢复矩阵优劣的衡量标准。MIP计算准则具有运算复杂度低、可行性高的优势，其原理是用不同矩阵的不同两列来表现两个矩阵的不相关性，可表示为：

当导频取值相同时，式（7）可简写成：

式中：w=e-j2π/N；T为恢复矩阵。

TSS算法的流程如图2所示。TSS算法原理描述如下：

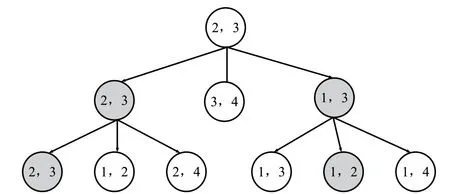
图2 TSS算法流程

假设1、2、3、4号子载波均可作为导频信号，并设每一代的存活节点个数为2。首先从1，2，3，4中随机抽取两个不同的数值，如2和3；其次将这两个数值作为导频位置索引，依次去除导频位置索引集中一个数值如2，此时导频位置的索引集合的差集为1，2，4这3个数值；最后将这3个数值依次与3组合求得该组合下的μ值，取两个最小值作为存活节点，并作为下次迭代的父节点，直到迭代结束。

3 仿真结果分析

当子载波数为512，导频插入方式采用梳妆插入方式时，得到图3、图4、图5、图6共4张仿真图。图3和图4分别在导频数目为32的情况下，采用随机导频插入方式和经过TSS算法计算之后的导频位置插入方式，同时运用基于压缩感知的信号重构SAMP和MMP-BF算法进行ACO-OFDM系统误码率的仿真。仿真结果显示，在无信道估计算法的加持下，系统的通信误码率是非常高的，而当加入信道估计算法后，系统的BER明显下降，并且在经过TSS算法运算后的导频位置插入时，系统的BER要低于随机导频插入时仿真得到的系统的BER，此时的μ=0.383 7；当BER为10-1时，在导频优化算法下，MMP-BF和SAMP算法信噪比分别为14 dB和29 dB；当信噪比为30 dB时，MMP-BF和SAMP算法的BER分别为9×10-3和8.23×10-2。

图3 导频为32且位置随机时的系统仿真

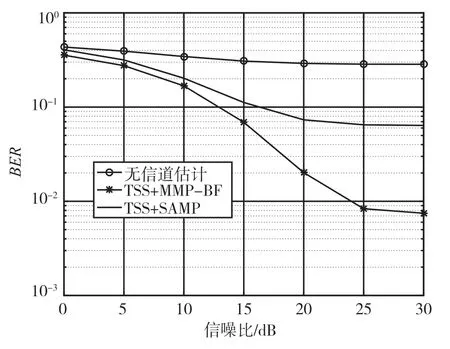
图4 导频为32且采用TSS算法时的系统仿真

当导频数为64时，仿真结果如图5、图6所示，此时的μ=0.251 6，且当BER为10-1时，在导频优化算法下，MMP-BF和SAMP算法的信噪比分别为15 dB和20 dB；当信噪比为30 dB时，MMP-BF和SAMP算法的BER分别为6.9×10-3和1.88×10-2。

图5 导频为64且位置随机时的系统仿真

图6 导频为64且采用TSS算法时的系统仿真

4 结语

本文通过介绍压缩感知技术和ACO-OFDM通信系统在NLOS通信环境下的通信特征，将信道估计技术与基于压缩感知的信号重构算法结合，并运用导频优化和信号重构算法，通过模拟仿真得到了相应的仿真结果。

本文采用基于压缩感知的导频优化算法TSS进行信道估计，降低了系统在NLOS环境下的误码率。同时将TSS算法和SAMP、MMP-BF算法相结合，仿真结果显示，在导频为32和64的ACO-OFDM系统中，在导频优化TSS算法下，信号重构算法SAMP估计准确性要低于MMP-BF算法，并且都远低于不使用信道估计算法的情况，可见信道估计技术对于提升通信系统的通信性能是非常重要的。