基于决策边界的倾斜森林分类算法

阚学达，桂 琼，张攀峰

(桂林理工大学 信息科学与工程学院，广西 桂林 541004)

0 引 言

作为多分类器的代表，由Leo Breiman提出的随机森林(random forests，RF)是分类算法的重要技术之一[1]。该算法被广泛应用于电力系统电荷预测[2，3]、入侵检测[4]、密码体制识别[5]以及图像分割[6]等方面。然而，该算法分类准确率还有待进一步提高[7]。此外，随机森林算法在分类不平衡数据集时，对少数类分类准确率过低，导致整体分类准确率下降[8]。因此，提高其对不平衡数据的分类准确率非常重要。对于处理不平衡数据方面，现有研究主要从数据集出发，将数据预处理融入到分类算法中[9]。文献[10]、文献[11]通过对抽样与投票的过程进行加权，使少数类有更高概率被抽样，并且对分类结果较好的决策树赋予更高的投票权重，有效提高随机森林对于不平衡数据的分类能力。在提高随机森林算法的分类准确率方面，文献[12]提出基于改进网格搜索的随机森林参数优化算法，通过寻找最优参数使得随机森林算法分类准确率有所提高。文献[13]将双边界支持向量机替代决策树的分裂准则，取得不错的效果。然而支持向量机的求解时间较长，增加每个结点求解分裂准则时间。针对进一步提高随机森林分类准确率并且使其适应不平衡数据分类，本文提出一种基于决策边界的倾斜森林(oblique forests based on decision boundary，OFDB)分类算法。OFDB算法把倾斜分裂超平面这一概念引入随机森林的分裂准则中。通过赋予各个类自适应权重，提高OFDB算法不平衡数据分类能力。为使算法可以解决多类分类问题，本文在单个结点分裂过程中采用“一对多”的策略。实验结果表明，OFDB算法分类准确率相比于的随机森林算法有较大提升，并且OFDB算法在处理不平衡数据集方面，比随机森林算法有更好的表现。

1 随机森林与决策边界

随机森林是由决策树组成的组合分类器，由装袋、决策树构建、袋外估计组成。

对于给定的n个元组m个属性的分类数据集

(1)

假设随机森林拥有k个单分类器，装袋的基本思想是，对于循环i(i=1,2，…，k)， 第i个决策树从训练数据集D中有放回地抽取n个元组，并且对被抽取的元组进行标记。

随机森林构建决策树常使用Gini指数作为分裂准则，用于衡量数据分区D的不纯度。基尼指数定义如式(2)所示[14]

(2)

pi表示D中元组属于Ci类的概率。考虑确定分裂属性A与确定分裂点的情况下，数据集D被该规则划分为D1、D2，该分裂准则的基尼指数计算公式如式(3)[14]

(3)

通过求解每个结点基尼指数GiniA(D)最小值得到每个结点最优分裂准则。最终得到k个决策树的分类模型序列 {h1(X),h2(X),…,hk(X)}。

随机森林预测采用多数投票法如式(4)所示[1]

(4)

其中，H(X)表示组合分类模型，hi是单个决策树分类模型。在预测中以多数表决的方法，得到随机森林总体的分类结果。袋外估计(out of bag estimation，OOBE)用来估计随机森林的分类能力，其使用每个决策树训练子集中没有被抽样的元组来对这个决策树进行测试。

逻辑回归是解决分类问题的一种常见算法。对于给定的样本属性X，y的取值如式(5)

hθ(X)=g(θTX)

(5)

其中，θ为权重参数，函数g如式(6)所示[15]

(6)

由式(5)、式(6)可知，当函数g(z)中z>0时，g(z)>0.5，此时预测该样本类别y取值为1。反之，当函数g(z)中z<0时，g(z)<0.5，此时预测该样本类别y取值为0。对于一个训练完成的逻辑回归模型hθ(X)=g(θTX)， 将样本Xi带入决策边界θTX计算该式是否大于0来判断该样本属于某一类。θTX=0被称之为该模型的决策边界。逻辑回归的代价函数如式(7)所示[16]

(7)

代价函数表示对于确定的θ模型对数据集X分类错误程度。对于给定数据集，X与y的值是确定的，θ为自变量，求解代价函数的最小值，即可求得分类错误程度最低时θ取值，确定决策边界。

2 OFDB算法

2.1 基本概念

定义1 倾斜决策树(Oblique Decision Tree)：倾斜决策树是以决策边界作为树中每个结点的分裂准则的决策树。假设类obliqueDecisionTree，对于该类的每个实例对象Node，变量classLabel表示当前结点的类标号；变量dataset表示当前结点的数据分区；变量leftChildTree与rightChildTree分别指向其左子树右子树；变量obliqueSplitHyperplane表示当前结点分裂超平面的θ值。

定义2 倾斜分裂超平面(Oblique Split Hyperplane)：OFDB算法中每个倾斜决策树结点Node的倾斜分裂超平面如式(8)所示

θT·X+θ0=0

(8)

传统随机森林算法分裂准则可表示为式(9)

x=b

(9)

其中，x表示某一确定属性，b表示确定常数。式(9)可由式(8)表示，即传统分裂准则为倾斜分裂超平的一种特例，倾斜分裂超平面考虑更为广泛的情况。在预测过程中，将新的样本元组X带入式obliqueSplitHyperplane·X中，以判断该样本位于倾斜分裂超平面的某一侧，进而被划分至左子树或右子树的数据分区中。对于特定的样本元组，计算如式(10)所示

obliqueSplitHyperplane·X= (θ0,θ1,…,θm)T·(1,x1,…,xm)

(10)

定义3 叶子结点标记自适应权重(leaf node labeling adaptive weights)：在决策树结点转化为叶子结点时，使用加权后的多数类标记该结点。叶子结点标记结果为式(11)

(11)

(12)

|D| 表示数据集D的样本个数， |DC| 表示数据集D中属于C类的样本个数。

2.2 基本思想

基于决策边界的倾斜森林分类算法是一种以随机森林作为框架，以倾斜分裂超平面作为决策树结点分裂准则的分类算法。其主要针对随机森林算法中的分裂过程做出改进，以此提高分类准确率。

在随机森林模型的框架下，构建k个倾斜决策树，并且为k个倾斜决策树进行有放回抽样并且舍弃重复元组作为训练子集。每个倾斜决策树递归地对每个结点进行分裂直至满足终止条件，之后将根据式(11)将对叶子结点进行类标记。

在传统随机森林算法中为求得最优分裂准则，通常会以最小化该结点Gini指数为目标。假设，求解得分裂准则为在属性ai(i=1,2,…,m) 上分裂点为常数b，即分裂准则为垂直于数据空间某一维度的超平面。但是这样的分裂方式不能很好抓住数据空间中的几何结构，文献[13]提出基于双边界支持向量机的倾斜决策树，但是由于支持向量机的求解时间过长，该方法仅在小数据集上具有较好表现。为保证构建倾斜分裂超平面的基础上提升运算性能，本文使用式(7)作为代价函数以求解超平面的θ参数作为倾斜分裂超平面。

考虑代价函数为凸函数，即函数局部最小值即是全局最小值，本文使用梯度下降法求解代价函数最小值。参数θ更新规则如式(13)

(13)

为保证梯度下降法迅速收敛，本文在训练之前使用式(14)对数据集进行规范化处理，将其取值映射至区间[0,1]之间

(14)

考虑在单个结点上通过一个超平面只能解决二分类的问题。为使算法可以解决多分类问题，本文使用“一对多”的策略，在单个结点使用最多类与其它类进行二分类，使算法适用于多分类问题。

考虑到正负类样本比例不同而对分类算法效果产生的影响，本文在叶子结点上设置如式(11)所示的类标签计算方法，按照样本中类的比例对叶子结点标记方法做出改进。

2.3 OFDB算法描述

算法1： OFDB分类算法

Input:dataset,targetattribute,maxDepth,estimators

Output: oblique forests.

(1)forT=1 toestimatorsdo

/*T表示每个决策树， 随机森林共有estimators个决策树*/

(2) call FIT function on randomly sampleddataset;

/*调用算法2， 递归地训练每个决策树*/

(3) save out-of-bag estimation result ofT;

(4)endfor

算法2： OFDB决策树结点训练算法FIT

Input:dataset,targetattribute,maxDepth

Output: oblique decision tree.

(1)ifdatasetis nullthen;

/*数据集为空， 则将当前结点转化为叶子结点*/

(2) Node convert to leaf;

(3)return0;

(4)endif

(6)ifNode.depth==maxDepththen

/*达到最大深度， 则将当前结点转化为叶子结点*/

(7) Node convert to leaf;

(8)return0;

(9)endif

(10)ifthe class of sample is purethen

/*数据集类纯粹， 则将当前结点转化为叶子结点*/

(11) Node convert to leaf;

(12)return0;

(13)endif

(14)fori=1 tondo

/*采用“一对多”的策略， 使算法适用于多分类问题。遍历n个元组的数据集， 将元组个数最多的类作为正类， 其余作为负类*/

(15)ifX[targetattribute][i]==majority class of Nodethen

(16) X[targetattribute][i]=1;

(17)else

(18) X[targetattibute][i]=0;

(19)endif

(20)endfor

(21) get obliqueSplitHyperplaneof Node fromdataset;

/*按照式(13)的更新规则， 求解式(8)倾斜分裂超平面， 保存为当前结点的分裂超平面*/

(22)fori=1 tondo

/*按照式(10)将当前数据元组按照分裂超平面继续划分给左右子树*/

(23)ifX[i]·splitCriterion≥0then

(24) divide X[i] into left child tree;

(25)else

(26) divide X[i] into right child tree;

(27)endif

(28)endfor

(29) create left child tree and call FIT function;

(30) create right child tree and call FIT function;

步骤1 OFDB算法中每个倾斜决策树进行训练子集抽样，舍弃每个子集中的重复抽样元组。

步骤2 递归地训练每个倾斜决策树。如果满足结束条件，则将当前结点转化为叶子结点。以加权的多数类赋值给当前结点的classLabel。将当前数据分区作为训练集，求解出倾斜分裂超平面θTX+θ0=0。 根据求解出的倾斜分裂超平面，计算式(10)obliqueSplitHyperplane·X的取值，将每个元组划分至左子树或右子树中继续训练。

步骤3 统计袋外估计结果，返回一个OFDB分类器。

2.4 算法分析与评价

2.4.1 算法正确性分析

对于给定的输入数据集，OFDB算法首先划分多个数据子集，分别用于训练每个倾斜决策树。对于给定的最大深度与决策树个数参数，决策树总会在满足条件时停止递归，并且标记该叶子结点。最终返回一个OFDB分类模型。在每个非叶子结点上保存倾斜分裂超平面θTX+θ0=0。 因此，每个预测元组总能通过倾斜分裂超平面被划分至子树中，最终到达叶子结点，返回叶子结点类标号作为该元组的预测值。

2.4.2 时间复杂度分析

假设OFDB算法决策树个数为e，最大深度为d。训练决策树均为满二叉树。对于一个深度为m递归生成的满二叉树，则递归时间复杂度为O(d2)。对于一个倾斜森林有e个倾斜决策树，则循环e次训练每个决策树时间复杂度为O(e)。假设数据集样本个数为n，属性个数为m，对于每个结点分裂过程，首先遍历数据分区，判断是否满足终止条件，时间复杂度为O(n)求解决策边界使用梯度下降法，求解梯度方向需要O(mn)，再对每个参数进行更新O(m)，迭代i次O(i)，则其时间复杂度不超过O(nm2i)。将数据分区划分给左右子树时间复杂度为O(n)。所以OFDB算法时间复杂度不超过O(ed2nm2i)。

2.4.3 分类性能分析

与RF算法的分裂准则相对比，OFDB算法将一个倾斜分裂超平面θTX+θ0=0作为分裂准则，而前者分裂准则可以表示为在m维的空间中使用超平面0×x1+…+1×xi+…+0×xm-b=0来划分所有的数据。RF算法分裂准则可表示为垂直于数据集空间中的某个属性轴的超平面，但是OFDB算法的分裂超平面不必垂直于某个属性轴，而是相对于RF算法的分裂准则是“倾斜”的，这使得OFDB算法分裂准则可以更适应数据集空间的几何结构。本文使用“倾斜”一词表明OFDB算法与RF算法分裂准则的区别。OFDB算法使用分裂超平面的同时也保留决策树结点分裂的可解释性。

2.4.4 评价指标

在分类准确性评价方面。以随机森林的袋外估计结果作为计算评价指标的依据，并使用混淆矩阵统计分类结果并且计算评价指标。Leo Breiman已经证明了随机森林中袋外估计的无偏性[1]。混淆矩阵见表1。

表1 混淆矩阵

其中TP表示被正确分类为正类的正类样本个数。FN表示被错误分类为负类的正类样本个数。FP表示被错误分类为正类的负类样本。TN表示被正确分类为负类的负类样本。本文使用准确率accuracy衡量分类器总体分类性能，使用TPR、FPR、F1-score来衡量分类器对不平衡数据的分类效果。

评价指标计算如式(15)至式(18)

(15)

(16)

(17)

(18)

TPR表示正类中被正确分类为正类的比例，在本文中正类表示少数类。FPR表示被错误分到正类样本中的负类样本所占比例。F1-score综合考虑正类与负类的准确率，是评价不平衡数据的良好指标。TPR与F1-score取值越高说明分类器对于少数类的分类性能越优。FPR取值高说明分类器对负类样本并没有很好的划分。

3 实验结果分析

3.1 实验数据集

实验主要分为2个部分：①通过人工数据集验证OFDB算法的可行性，并将倾斜分裂超平面可视化与RF算法的分裂准则比较；②使用真实数据集横向对比OFDB算法与RF算法，以分类准确率等评价指标来衡量分类效果。真实数据集名称、样本个数、属性个数以及样本类分布情况见表2。所有数据集中的元组不含缺失值。在训练之前，对于数据集中离散的标称属性，统一设置虚拟变量。

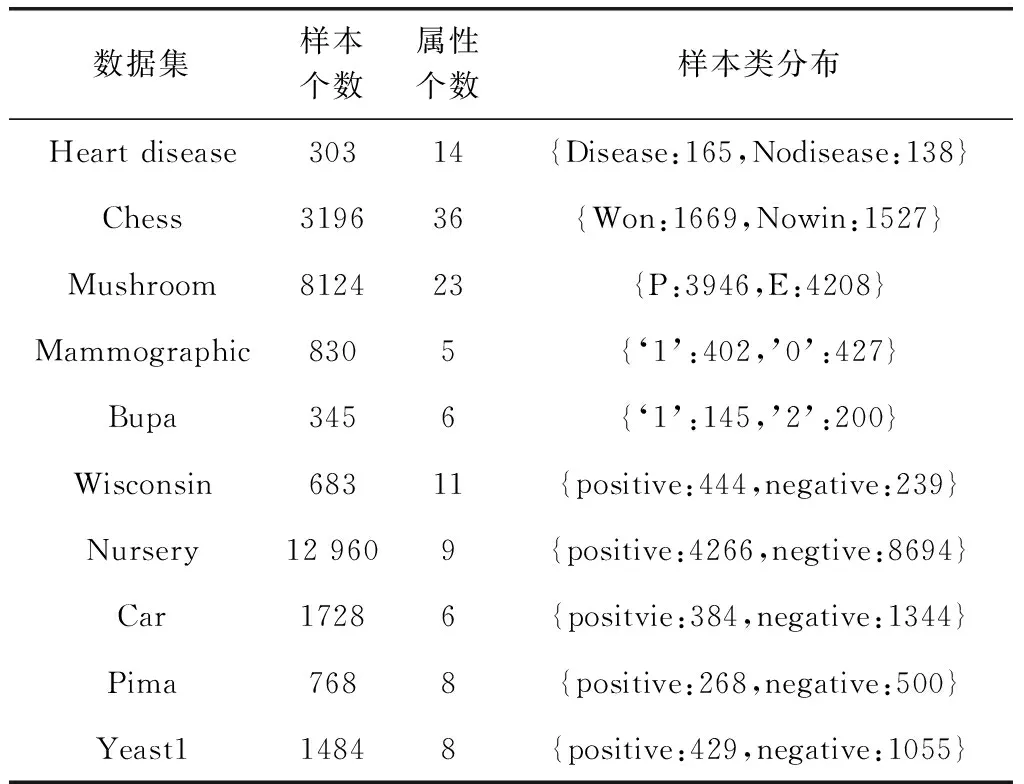
表2 数据集说明

3.2 实验结果分析

实验1：OFDB算法与RF算法分裂准则对比实验

为了将分裂准则可视化，人工数据集维度为2维。使用互相独立的正态分布随机生成比例相同的正负类样本点。实验直观表示了OFDB算法与RF算法分类过程的区别。OFDB算法倾斜分裂超平面与RF算法分裂准则如图1、图2所示。

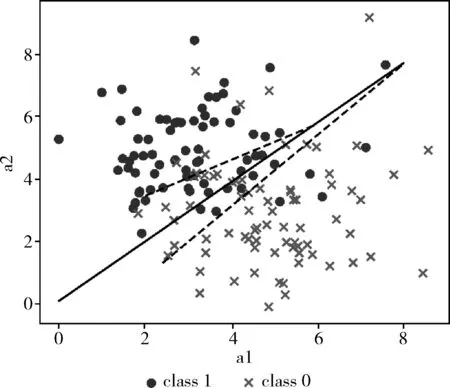
图1 OFDB算法倾斜分裂超平面

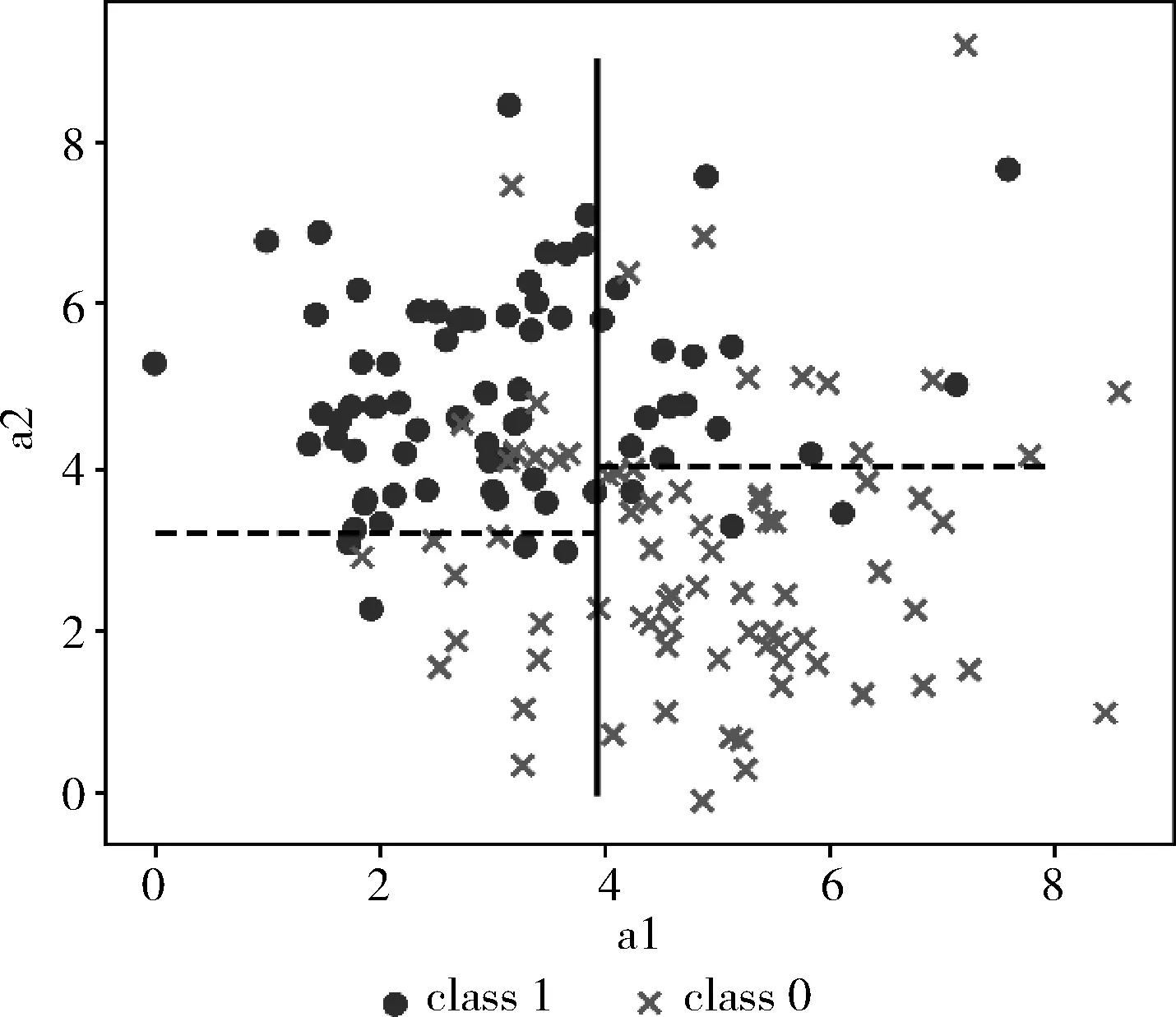
图2 RF算法分裂准则

图中不同样式的点代表两类不同的元组，直线代表决策树深度为0的根结点的划分，每颗决策树的根结点只有一个。而两条虚线代表决策树中深度为1的结点的划分，深度为1的结点有两个，分别是根结点的左子树与右子树结点。随着决策树深度的增加将会有更多的划分对数据进行分区，最终以每个区域的多数类标记该区域，以此来进行预测。由图1、图2可知，RF算法的分裂准则必是垂直于数据集空间中的某个属性轴的超平面，OFDB算法则是以一个“倾斜”的超平面对数据集进行划分，RF算法的分裂准则可以由OFDB算法的倾斜分裂超平面所表示出来，因此OFDB算法倾斜分裂超平面可以考虑到RF算法分裂准则的所有分裂情况。

实验2：OFDB算法与RF算法分类结果对比实验

实验2使用准确率与其它不平衡数据评价指标对OFDB算法与RF算法的分类结果进行对比。以分类准确率做为评价指标。最大深度参数maxDepth分别取3，5，7；决策树个数参数estimators分别取5，10，20。表3至表7

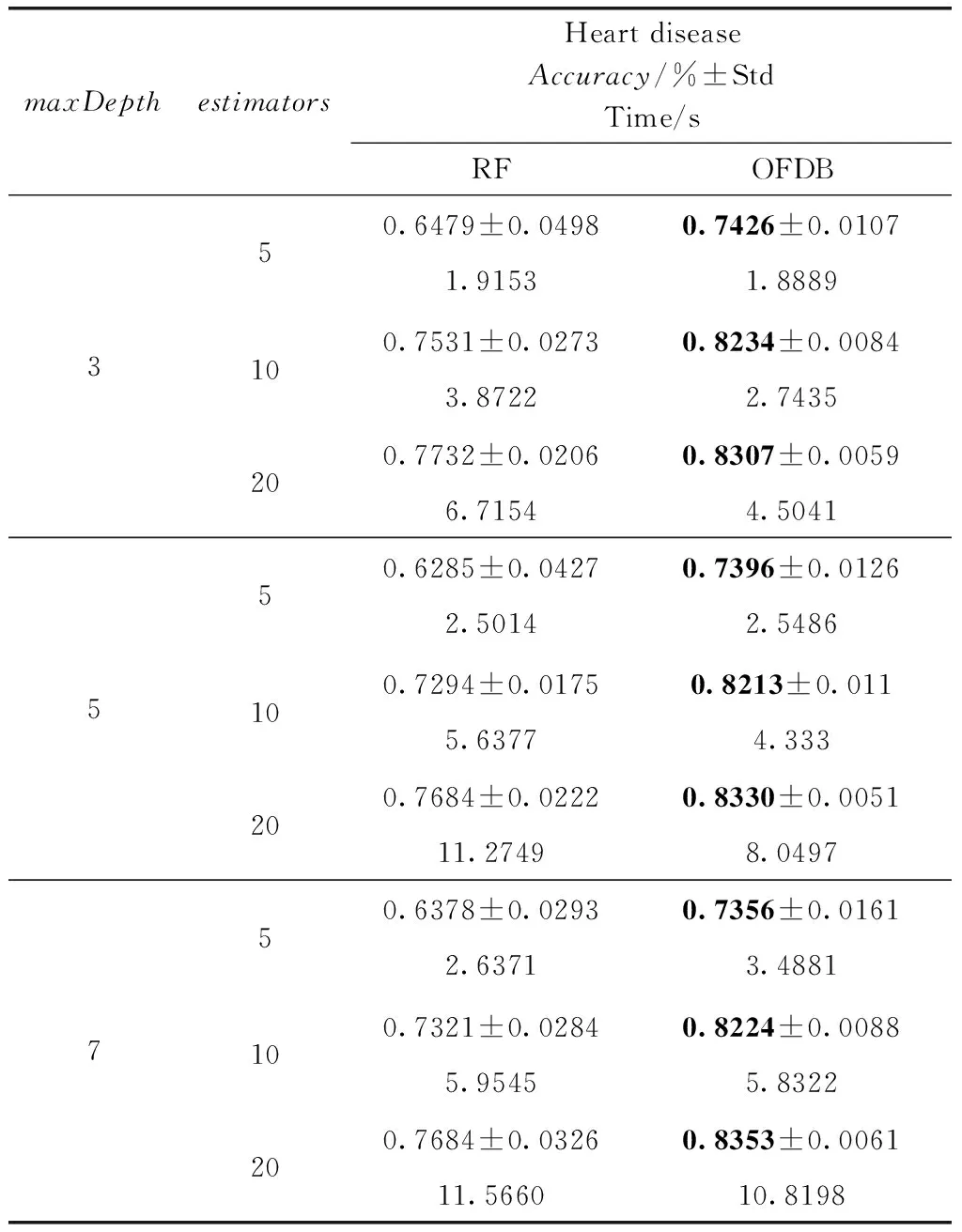
表3 Heart disease数据集分类准确率对比

表4 Chess数据集分类准确率对比

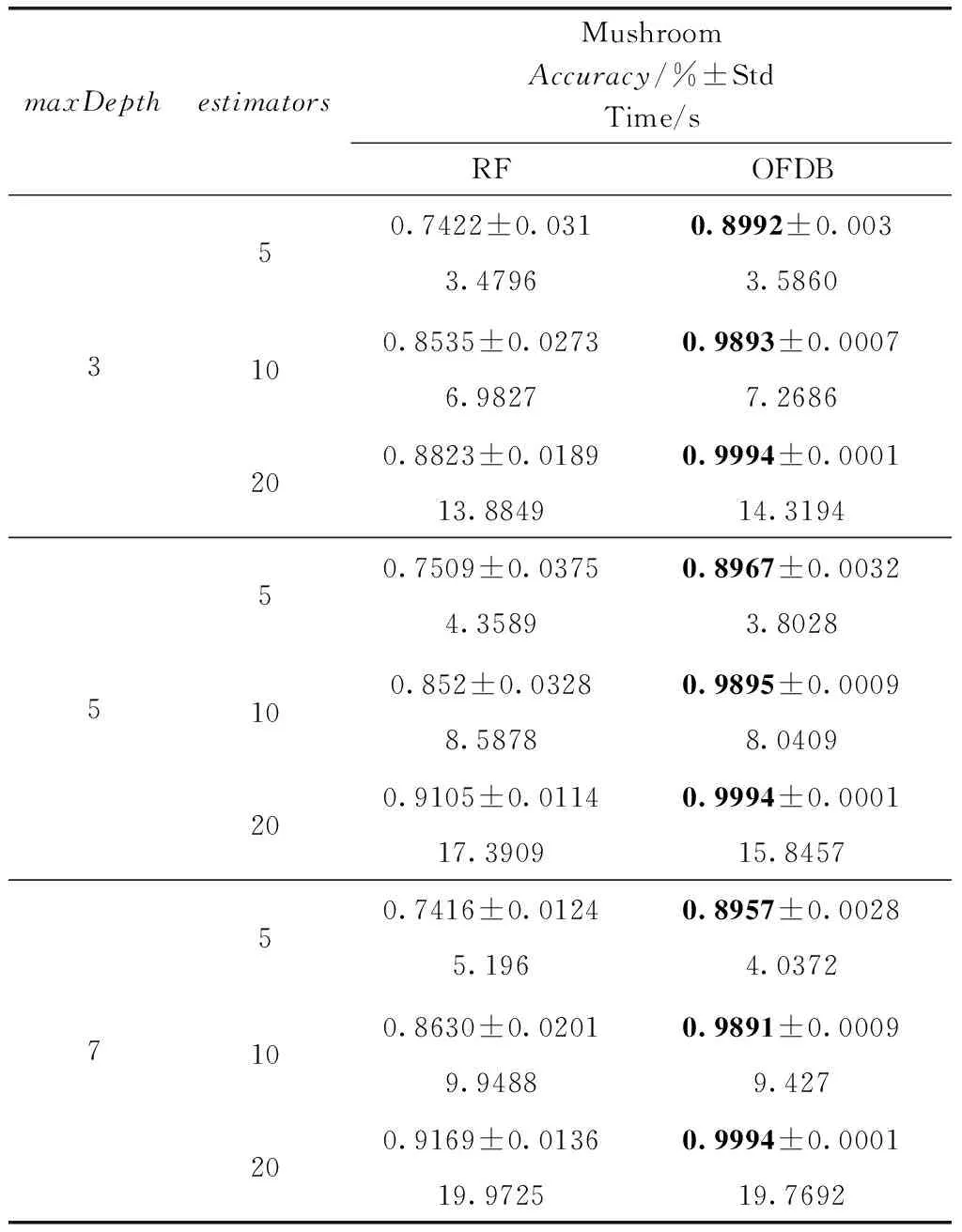
表5 Mushroom数据集分类准确率对比

表6 Mammographic数据集分类准确率对比

表7 Bupa数据集分类准确率对比

展示5组实验，分别在5个数据集Heart disease、Chess、Mushroom、Mammographic、Bupa上，使用不同的参数，展示袋外估计分类结果的准确率。其中较优的实验数据使用粗体标出。为减小随机数所产生的单次实验结果不确定性，所以在本次实验中，实验结果取10次实验的平均值，并且计算标准差与运行时间。

观察表3至表7可以得出，对于Heart disease、Chess、Mushroom、Manmographic、Bupa数据集，OFDB算法分类准确率高于RF算法。随着estimators的增加，OFDB算法的分类准确率有所提高。然而在estimators大于10后，总体的分类准确率提高较少。对比estimators取值10和20的情况，多出一倍的决策树个数却只得到分类准确率0.01左右的提升。随着参数maxDepth的增加，OFDB算法的分类准确率并没有明显的提升。这可能是因为主要的分类工作是在深度较低的结点中完成的，剩余少数样本OFDB算法难以划分。对比标准差，OFDB算法明显具有优势，分类结果具有较高的稳定性，这是由于使用决策边界替代了原具有较高随机性的结点分裂准则。主要体现在候选分裂属性随机选取。运行时间方面，OFDB运行时间与RF运行时间相差不大。

为表明OFDB算法相比于RF算法对于少数类分类有更优异的性能，以不平衡数据评价指标TPR、FPR以及F1-score衡量分类效果。如表8所示，针对参数maxDepth取值5，estimators取值10的情况，给出OFDB算法与RF算法在5个不平衡数据集Wisconsin、Nursery、Car、Pima、Yeast1上的对比结果。观察表8可以得出，对不平衡数据集的分类OFDB算法相比RF算法具有更好的效果。

表8 不平衡数据集上OFDB算法与RF算法不平衡分类指标对比

4 结束语

本文提出一种基于决策边界的倾斜森林分类算法OFDB。OFDB算法使用倾斜分裂超平面来改进RF算法中的结点分裂过程。针对不平衡数据处理分类问题，使用自适应权重改进叶子结点的类标号。为使算法适用于多类分类问题，在结点分裂过程中采取“一对多”的策略。实验部分，使用人工数据集直观对比OFDB算法与RF算法的分裂过程。通过真实数据集的实验结果显示，OFDB算法相较于RF算法具有更良好的分类性能，并且对不平衡数据分类能力有所提高。但对于极度不平衡数据集，OFDB算法分类效果仍较差。之后的研究中将侧重于提高分类器对于不平衡数据集的分类能力，以及提高分类算法训练效率。