对称极坐标牛顿法潮流的直角坐标解法

陈 恳，廖嘉文，熊守江，丁 戈

(1. 南昌大学信息工程学院，江西 南昌 330031；2. 国网江西检修公司，江西 南昌 330096；3. 国网睢宁县供电公司，江苏 睢宁 221200)

1 引言

牛顿-拉夫逊法潮流(牛顿法)因具有平方收敛的特性[1]，是电力系统潮流计算中最常用的方法[1-6]。根据其节点电压的表达方式，可分为极坐标和直角坐标牛顿法。极坐标牛顿法与直角坐标牛顿法相比，对计算速度有利的主要因素为：需求解的方程数量和需计算的雅可比矩阵J中元素数量较少，且PV节点数越多其数量越少；潮流迭代次数一般相同，但有时可能少1次。但另一方面，极坐标牛顿法中J阵元素、节点电流Ipi和Iqi、节点功率ΔPi和ΔQi的计算中均含大量三角函数，对其计算速度又产生了不利因素。但三角函数的影响往往容易被忽略。上述因素均易导致极坐标牛顿法比直角坐标牛顿法的计算速度更快的观念。尽管极坐标牛顿法的求解方程数、J阵元素计算数甚至潮流迭代次数上具有优势，但其大量三角函数计算完全可能使其失去对直角坐标牛顿法的速度优势。此外，个别文献将直角坐标牛顿法的J阵用子阵表示[3]，但并未提出任何具体应用技巧。且由于极坐标牛顿法的J阵与直角坐标牛顿法相比结构更不对称，因此没有文献将极坐标牛顿法J阵用子阵表示，这对极坐标牛顿法中J阵元素的计算分析极为不利。

目前对牛顿法的各种改进算法多为引入新的算法与传统牛顿法相结合。如在牛顿法基础上引入张量概念，将展开泰勒的潮流方程保留二次项[7-8]；在牛顿法基础上引入最优乘子从而改变迭代步长[9-10]；将牛顿法与梯度法相结合，并在此基础上引入阻尼因子，自适应选择迭代步长和方向的LM方法[11-14]。虽然这些改进方法各有所长，但均有计算原理复杂、计算量大，程序编写困难等问题，且仍未解决极坐标牛顿法中J阵元素不对称以及三角函数计算等问题。

针对上述问题，本文提出一种对称极坐标牛顿-拉夫逊法潮流的直角坐标解法，其中包括：建立结构不完全对称的子阵形式的J阵，通过子阵建立子阵间元素的对应关系；拆分J阵元素的计算以建立其元素的部分对称关系；对J阵元素等计算公式进行三角变换，并按“二行+二列”的方式对称计算J阵元素；用四角规则而不是消元计算公式对J阵元素消元计算；将取倒的对角元素作为规格化因子以减少除法计算等。

2 极坐标J阵中元素的部分对称关系

为克服J阵元素的不对称导致计算效率低的问题，可通过建立子阵形式的J阵，并拆分J阵元素的计算来建立J阵元素部分对称关系。假设系统节点数为n，PQ节点数为m，m+1及其后节点均为PV节点，第n个节点为平衡节点。根据子阵元素分布可将J阵分为1～4区，并分别以Jij子阵及其元素Hij、Nij、Mij、Lij和Jji子阵及其元素Hji、Nji、Mji、Lji两种方式排列J阵，对应的修正方程如式(1)。

(1)

2.1 非对角元素的部分对称关系

由于对J阵元素中Hij≠Hji、Nij≠Nji、Mij≠Mji、Lij≠Lji的固有观念，传统方法形成J阵时均分别利用各个子阵Jij、Jji中元素的独立关系Hij=Lij、Nij=-Mij和Hji=Lji、Nji=-Mji，但无法利用Jij、Jji子阵中元素的对应关系，从而须分别求取Jij、Jji子阵中元素，导致形成J阵速度不理想。

为建立Jij、Jji子阵中元素的部分对称关系，可拆分Jij、Jji子阵中各非对角元素(j≠i)计算式如下

(2)

其中c1、d1、c2、d2计算式可分列如下

(3)

因此计算出式(3)中c1、d1、c2、d2四个分离变量，就可分别得到式(2)中Jij、Jji子阵中的八个元素Hij、Nij、Mij、Lij和Hji、Nji、Mji、Lji，即拆分计算不但可利用Jij子阵中元素Hij=Lij、Nij=-Mij的关系，还可利用其与Jji子阵中元素Hji与Hij、Nji与Nij、Mji与Mij、Lji与Lij之间的关系，以及Jji子阵中元素Hji=Lji、Nji=-Mji的关系。

对应式(1)中J阵的1～4区，可分别按三种情况完成元素的部分对称计算如下：

1)对1区元素计算，如J1m、Jm1子阵中元素H1m、N1m、M1m、L1m与Hm1、Nm1、Mm1、Lm1对应，计算出c1、d1、c2、d2四个变量，可得到所有八个元素。

2)对2区和3区元素计算，如J1，m+1、Jm+1，1子阵中元素H1，m+1、M1，m+1与Hm+1，1、Nm+1，1对应，计算出c1、d1、c2、d2四个变量，可得到所有四个元素。

3)对4区元素计算，如Jm+1，n-1、Jn-1，m+1子阵中元素Hm+1，n-1与Hn-1，m+1对应，计算出c1、d1二个变量，可得到所有二个元素。

上述计算过程表明，J阵元素的计算总是以对角子阵Jii为参考，Jij子阵和Jji子阵同时对称完成计算。如果以四个对角元素为参考，J阵元素的计算是以“二行+二列”的对称方式完成计算，而不是传统方法中的按行或按二行方式计算。此外，由于系统中PQ节点数远多于PV节点数，因此在形成J阵时绝大部分的计算是对1区元素的计算，对2～3区元素的计算也较多的，而对4区元素的计算较少。因此通过对Jij、Jji子阵中元素的部分对称计算，可大大加快J阵元素的计算。

2.2 对角元素的部分对称关系

由于J阵对角元素的叠加运算以及对Hii≠Lii、Nii≠-Mii的固有观念，因此无法建立元素的部分对称性，所以需单独计算Jii子阵中元素Hii、Nii、Mii、Lii，也导致形成J阵速度不理想。此外，传统方法中J阵对角元素几乎全部以节点电压方式计算，文献[3]虽给出了以节点功率方式计算，但其表述方式并未展示和利用J阵对角元素的部分对称关系。

为建立Jii子阵中元素的部分对称关系，可拆分Jii子阵中以节点功率方式计算的各对角元素(j=i)计算式，拆分后的计算式如下

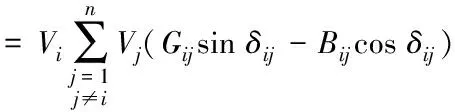
=Hij|i=j+Qi=H′ii+Qi

=Nij|i=j-Pi=N′ii-Pi

=Mij|i=j-Pi=M′ii-Pi=-N′ii-Pi

=Lij|i=j-Qi=L′ii-Qi=H′ii-Qi

(4)

式(4)中第一部分公式是绝大部分文献中以节点电压方式计算的传统方法，均涉及叠加运算，但该部分计算实际上包含了对节点功率Pi、Qi的计算。由于在生成J阵之前求取不平衡量ΔPi、ΔQi时已经求解了Pi、Qi，如果分别用式(4)中第一部分公式计算元素Hii、Nii、Mii、Lii，则意味着对节点功率Pi、Qi的重复计算。

上述分析表明，通过拆分J阵元素的计算过程，不但可实现J阵中Jij、Jji对称子阵中元素的部分对称计算，还可实现Jii子阵中元素的部分对称计算，从而可大大加快J阵的形成速度。

3 极坐标J阵中元素的三角变换

极坐标牛顿法中J阵元素涉及大量三角函数计算，对其进行三角变换可极大地减少程序中三角函数计算，同时应用极坐标牛顿法方程数较少的特点求解潮流，从而大大提升计算速度。

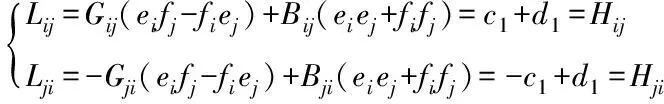
(5)

此时c1、d1、c2、d2的计算式分别如下

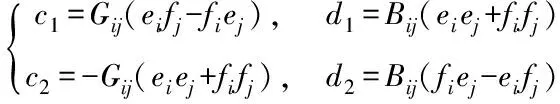
(6)

由于对角元素的计算可分为以非对角元方式计算对角元素，再用Pi、Qi进行修正两步，第一步已在式(5)～(6)得到解决，而Pi、Qi的计算可通过直角坐标形式的式(7)～(8)完成。因此根据式(5)可完成极坐标非对角元素的直角坐标对称计算，而通过式(4)～(8)可完成极坐标对角元素的直角坐标对称计算。

(7)

(8)

4 极坐标J阵中消元计算的四角规则

传统极坐标牛顿法潮流方程的求解均依赖消元计算公式，不利于对计算过程的理解和技巧的应用，更不利于编程。实际上，对消元计算过程稍加分析可以发现，由于消元过程的分步计算，每次参加计算的相关元素均在其矩阵的四个角上。因此消元计算完全可以不用消元计算公式，直接根据参加消元计算的元素在矩阵中的位置进行消元计算。此外，传统极坐标牛顿法在求解方程时和其它传统方法一样，也未考虑规格化因子对计算速度的影响。如果在消元计算过程中，将取倒后的对角元素作为规格化因子，可大大减少程序中的除法计算，因而提高计算速度。

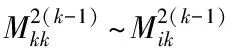
(9)

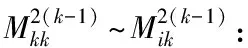
传统高斯消元计算公式可用文字表述为：对角元素为参考元素，计算元素新值=其前值-消元元素*规格化后交叉元素。据此表述可直接写出各个计算元素的新值如下：

(10)

由于参与计算的四个相关元素均在矩形的四个角上，故称四角规则。因此根据四角规则，即根据元素在矩阵中位置可直接写出各元素的相应消元计算式而无需消元计算公式，更无需考虑元素上下标等因素。

5 算例分析

用传统极坐标牛顿法和本方法计算IEEE-14～-118节点系统潮流，收敛判据为ε≤10-5。两种方法生成J阵的平均时间、潮流计算的平均时间、迭代次数及其比较见表1。

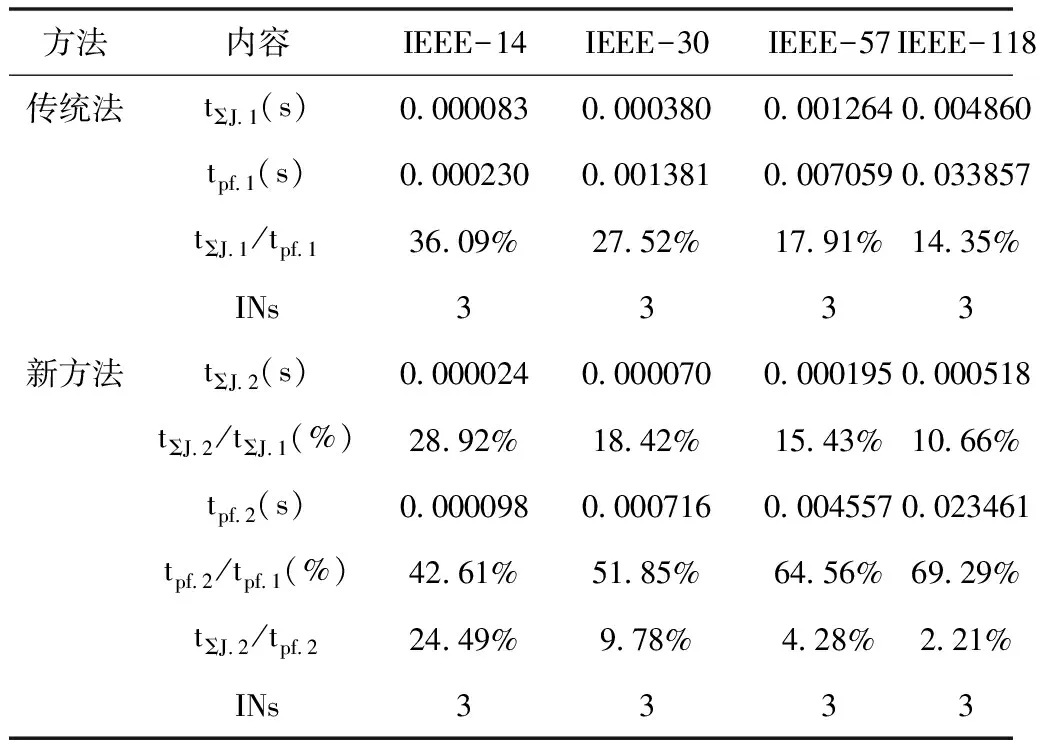
表1 传统法与本方法对比

(注：tΣJ：生成J阵的平均时间；tpf：潮流计算的平均时间；INs：潮流计算迭代次数。)

以IEEE-118节点系统为例，本方法与传统极坐标牛顿法相比，主要优势为：生成J阵速度大大提高，且随着系统规模的增加而增加。如传统法中生成J阵的平均时间约为潮流计算时间的14.35%，但本方法中约为2.21%；而本方法生成J阵的平均时间约为传统法的10.66%。此外，在同样收敛精度和迭代次数的情况下，本方法潮流计算的平均时间约为传统法的70%。

6 总结

本方法综合利用极坐标牛顿法中J阵元素少、方程数量少以及直角坐标牛顿法中没有三角函数计算的特点，并克服极坐标J阵元素的不对称使其计算速度不理想的情况，提出一种对称极坐标牛顿-拉夫逊法潮流的直角坐标解法。其主要内容为：将极坐标牛顿法J阵元素用子阵表示，以展示其对应关系；按子阵拆分J阵元素的计算，建立J阵元素的部分对称性，按“二行+二列”的对称方式计算J阵元素，以大大提高J阵的形成效率；对J阵元素及其节点功率计算公式进行三角变化，以大大减少程序中的三角函数运算；消元计算中将取倒后的对角元素作为规格化因子，以大大减少程序中的除法计算。上述计算过程可快速形成J阵，较大幅度地提升潮流计算速度。此外，本方法应用四角规则直接根据元素在矩阵中的位置完成消元计算，无需消元计算公式可简化计算过程、并极利于程序编写。