基于线控转向系统的电机控制算法研究
2022-03-01李展峰施卫刘斌常嘉伟
李展峰,施卫,刘斌,常嘉伟
(江苏理工学院 机械工程学院,江苏 常州213000 )
0 引言
转向作为汽车“动、停、拐”三大功能之一,对驾驶员的操作舒适性以及安全性有着至关重要的作用。近年来,随着中国对稀土材料的重视和对高性能稀土永磁材料的开发与应用,以及国内研究人员对电机控制算法、控制理论的深入研究,永磁同步伺服系统得到了广泛的应用。永磁同步伺服系统具有较高的定位精度和稳速精度,使其作为汽车转向的执行机构,可以很好的实现汽车前轮转角对方向盘转角的跟随控制。
目前,电机控制算法主要是基于电流环和速度环对电机转速进行控制,而线控转向系统是通过角位移信号控制电机。因此,在现有的电机双闭环控制算法的基础上增添位置环,并对原有的电机控制算法进行优化,从而实现汽车转向的“线控”,有利于推动汽车向智能化、自动化发展。
1 永磁同步电机的数学模型
永磁同步电机在设计控制系统时,存在许多外界因素和干扰,因此很难搭建精确的数学模型,而且其被控对象随着时间的变化而变化,属于非线性系统,具有变量多、参数难耦合等特点,影响电机性能。所以在搭建电机数学模型时,一般忽略永磁同步电机的铁芯饱和现象,假设其电流为三相正弦电流并且对称,电动机产生的涡流和磁滞损耗一般不做考虑。由此搭建的正弦波电机数学模型,有利于分析永磁同步电机的瞬态性能以及电机运行时的稳态性能。在对永磁同步电机进行数学建模时,为了简化其数学模型,通常采用自然坐标系、、、静止坐标系(,)以及同步旋转坐标系,3种坐标之间的关系如图1 所示。

图1 各坐标之间关系图Fig.1 A diagram of the coordinates
为了方便在simulink 中搭建其数学模型,采用同步旋转坐标系下的数学模型为:
(1)转子参考电压下的电压方程:

式中, i、i,u、u,ψ、ψ分别为永磁同步电动机定子的电压以及磁链在、轴分量,ω是电机转子电角速度。
(2)磁链方程:

式中,L、L为定子绕组、轴电感,Ψ是电机转子永磁体产生的磁链。
(3)电磁转矩方程:

式中,T和分别为电机电磁转矩和电机转子极对数,ψi为磁阻转矩。
磁阻转矩是由凸极电机气隙不均匀的凸极效应而产生的,磁阻转矩的大小将会影响到电机转矩的输出大小。而隐极式同步电机的励磁绕组是沿转子呈圆周阶梯式分布,转子不会形成凸极效应。其定子绕组在、轴上的电感相等,所以隐极式同步电机的电磁转矩方程为:

2 永磁同步电动机矢量控制原理
由隐极式同步电机的电磁转矩方程可以看出,电动机的电磁转矩与其电流在轴的分量成正比。当电流在轴的分量为0 时ψi=0,即磁阻转矩为0。此时,定子磁动势空间矢量与永磁体磁场空间矢量相互正交,单位定子电流可以获得最大的电磁转矩,有利于充分利用电机的输出能力。在满足驾驶员完成转向所必需的电机转矩前提下,输入最小的定子电流,从而使转向电机内部铜耗下降,电机效率有所提高。所以在电流环采用i=0的控制方法。
2.1 电压空间矢量控制原理
空间矢量调制技术(SVPWM)的主要思想是以电动机在理想状态下输出的定子理想磁链圆为标准,适当的切换三相逆变器不同的开关模式组合,生成PWM 波,然后,形成实际的磁链矢量跟随理想磁链圆,从而输出满足期望的电磁转矩。为了保护电路,三相两电平电压逆变器的同一桥臂的上下开关不允许同时导通,故逆变电路共有8 种开关组态,形成2个零矢量和6个基本电压矢量。
从图1 基本电压矢量示意图可以看出,6个基本电压矢量、、、、、按照逆时针的顺序将平面分成了6 份,形成6个扇区,且在一个工作周期内各出现一次。所以任何所需的电压矢量在任意一个扇区都可以由相邻的两个基本电压矢量和零矢量合成得到。

图2 基本电压矢量示意图Fig.2 Basic voltage vector diagram
2.2 SVPWM 控制算法
SVPWM 算法通过分配三角波周期的占空比,从而计算出切换点T、T、T。由切换点就可以与三角波比较,生成相应的PWM 波来控制逆变电路。
2.2.1 计算扇区

式中,如果V >0,则1,否则0;如果V >0,则1,否则0;如果V >0,则1,否则0。 V、V、V是参考电压矢量V在(,,)坐标系下的投影,可由(,)坐标系下的V、V经过Clarke 逆变换求出:

2.2.2 计算作用时间
电压矢量作用时间关系如图3 所示:

图3 电压矢量作用时间Fig.3 Voltage vector action time diagram
判断出扇区后,、就是此扇区相邻两电压矢量的作用时间。假设参考电压V位于第三区,则、是指、,V通过映射到(,)坐标系下得出:

由图3 可知,、在(,)坐标系下的关系,则每一个相邻相量作用时间为:
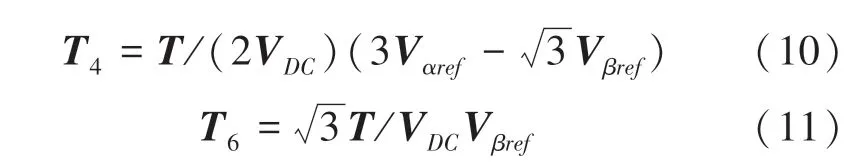
定义变量、、且、,则:

2.2.3 计算占空比
五段式和七段式是SVPWM 常用的两种调制方式,两种调制方式的区别为零矢量的插入方式不同。由于七段式调整方式在矢量切换的过程中只有一项状态发生改变,而且三相状态在一个开关周期内均各变化一次。开关次数较少,可以减小开关损耗并且产生较小的谐波分量,所以本文采用七段式调整方式。
、、三相电压在一个PWM 周期中导通占空比为:
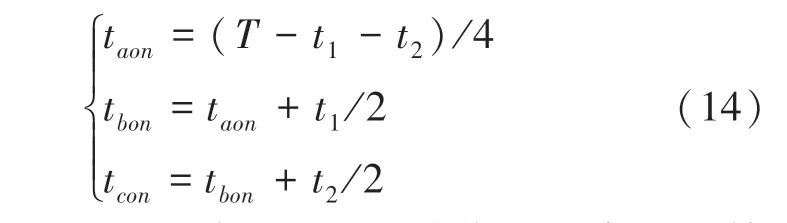
式中,t、t、t分别是一组开关作用顺序下的第一次至第三次开关切换时间。
3 三闭环参数整定
3.1 电流调节器参数整定
本文所搭建的电流环采用i=0的控制方法,电流环应满足在转向执行时,电流没有较大的超调量,而且整个系统响应及时。所以,将电流环矫正为典型的I 型系统。
由于电流内环有逆变器和PWM 控制的小惯性环节,系统采用PI 控制器进行控制。在不考虑ωφ带来的扰动影响情况下, T表示电流环的采样周期,并且将PI 调节器的传递函数化为零极点的形式:

将系统的两个时间常数T合并,得到电流环简化结构,如图4 所示:经过PI 调节器的校正后,得到电流环的闭环传递函数为:

图4 q 轴电流环的简化结构框图Fig.4 Simplified block diagram of q axis current loop

由于开关频率较高所以采样时间T极小,公式(16)的后项可以忽略不计,由此可得:

因该系统是典型I 型系统,所以通过查询其动态性能指标参数表可知,当系统为最佳二阶系统时,阻尼比0707。由此可得:
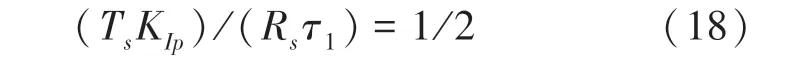
电流环的PI 参数为:

3.2 转速调节器的参数整定
转速环包含电流内环,将电流内环等效小时间常数4T与速度信号采样的小时间常数τ进行合并,得T=5T。将负载转矩T当作扰动引入,由于粘连摩擦系数在工程中可忽略不计,且先忽略负载转矩,则得到转速外环的结构如图5 所示:
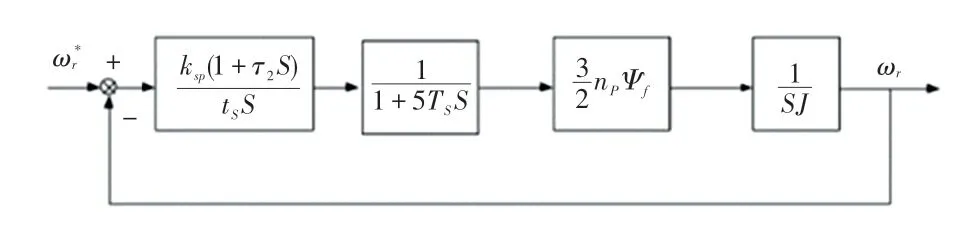
图5 转速外环的简化结构框图Fig.5 Simplified structure diagram of the outer ring of the rotational speed
由此可求得开环函数为:

转速外环的中频带宽h为:

根据典型II 型系统的参数整定关系可得:

在工程应用中,一般取中频带宽h=5,可得:

进而可以推导出转速外环的PI 参数为:
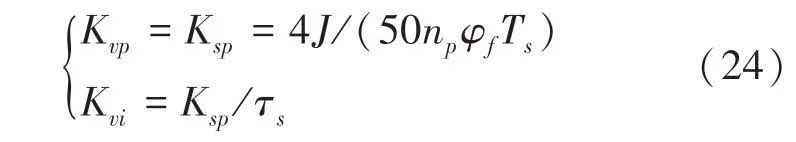
3.3 位置环参数设计
本文选定永磁同步电机作为线控转向的执行电机,在转向执行过程中,电机要对方向盘转角的输入进行实时跟随控制,且不允许出现超调,所以设计位置环为比例控制。但是,单用比例来控制电机很难消除稳态误差,所以在速度环前添加前馈控制。位置环的简化控制结构如图6 所示。

图6 位置环的简化结构框图Fig.6 Simplified block diagram of position ring
首先,确定速度环前馈的传递函数为:

根据图4 可得位置环的开环传递函数为:

进而得到位置环闭环传递函数为:

速度环系数在引入速度前馈之前应为0,此时可求出位置闭环传递函数为:
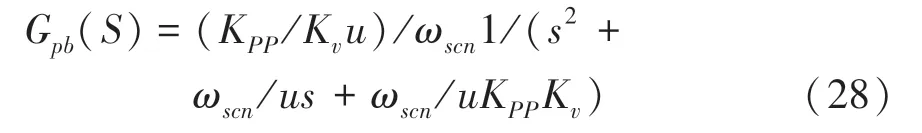
由此可知,在未引入速度前馈时,位置环可以视为一个典型二阶系统。为了实现方向盘转角对汽车前轮转角的跟随控制,位置响应不应出现超调,所以上式应为临界阻尼二阶系统。则有:
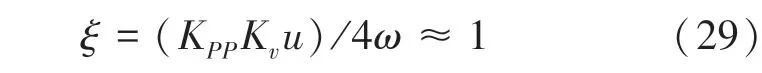
其中,为阻尼比,故有:
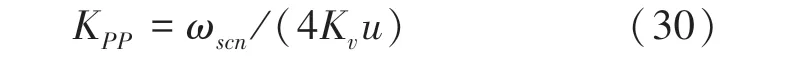
可以得到位置环误差传递函数:

当位置指令为斜坡给定时,位置环稳态误差可表示为:
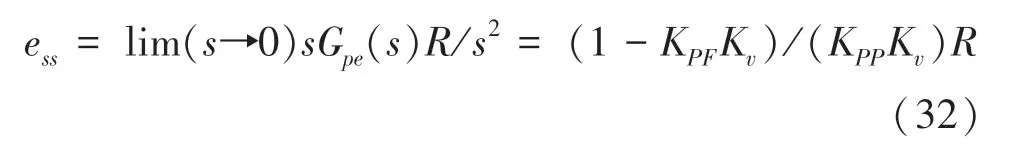
为使位置环稳态误差e=0,则有K=1/K。通常将前馈控制器设计在欠补偿状态,所以应引入补偿系数(0 ≤≤09),从而得到速度前馈增益为K=λ/K。
综合可得位置环控制器参数:
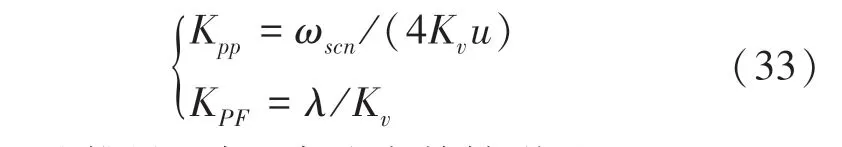
由上述推导可知,当速度前馈增益K≤1/K时,可以通过增大速度前馈增益,从而减小位置环稳态误差。但当K >1/K时,位置响应会出现超调,这在转向过程中是不允许的,会对驾驶员的生命安全造成隐患,所以需要引入补偿系数。
4 仿真模型的搭建及对比分析
4.1 模糊控制器的搭建
本文在速度环采用模糊PI的控制方法,在线随时调整PI 参数,提高了速度环的工作能力和稳定能力。其工作原理为:将车辆行驶过程中转向电机的转速期望值与此时传感器测得的电机转速实际值进行做差,以差值作为模糊控制器的输入,依靠专家经验和实验经验,制定相应比例与增益的模糊控制规则,再经过推理机、解模糊化等,得到新的速度环PI的补偿量。
4.1.1 确定输入输出及论域
模糊控制器的输入为转速误差和转速误差变化率;输出为比例增益补偿量ΔK以及积分增益补偿量ΔK。和的论域为{3,2,1,0,1,2,3}; ΔK和ΔK的论域为:{03,02,01,001,02,03}。
4.1.2 模糊化和隶属度函数
在设计模糊控制器时选用三角隶属函数作为隶属度函数。模糊化后使得模糊变量落在论域内。

式中,、为量化因子; a和a为论域范围; N和N为模糊集合个数。
4.1.3 去模糊化
由于按照模糊规则模糊推导后,其结果仍然是一个模糊矢量,不能直接作为控制量,所以必须将模糊量转化为实际用于控制的清晰量进行补偿。

式中,为输出清晰量,μ为各组元素权重。由此在simulink 中建立模糊控制器的仿真模型如图7 所示。

图7 模糊控制器模型图Fig.7 Fuzzy controller model diagram
4.2 建模与仿真分析
图8 是模糊控制器补偿调节后的K与K的值。从图中可以看出, K与K的值随着工况进行实时调节,调节到一定数值后,相对稳定在一个固定的值。004 s 时给电机一个突加负载,此时K、K先是大幅度变换后,在极短的时间内回复稳定。所以该模糊控制具有较强的自适应性和较快的反应速度,可以对系统执行过程中的比例和积分系数进行快速补偿。

图8 模糊控制器输出的Kp、KiFig.8 Fuzzy controller output Kp, Ki
图9 为传统PI 控制和模糊PI 控制的转速输出对比图。其中,红色曲线为传统PI 调节输出的转速图,蓝色是经过模糊控制补偿PI 后的转速输出曲线。通过对比可以看出,传统PI 控制的转速输出具有一定的超调和震荡,调节时间较慢;而由模糊PI控制器所控制输出的转速在0.015 s 内便达到了转速期望值,并且没有超调和震荡,当在0.04 s 给电机突加负载后,系统相对稳定,转速先是在小范围下降然后快速达到目标值。

图9 转速输出对比图Fig.9 Speed output comparison diagram
图10 为转矩输出对比图。其中,蓝色曲线是传统PI 控制电机的扭矩输出,红色是经过模糊控制后的电机扭矩输出。从图中可以看出,模糊控制器比传统PI 控制的扭矩输出,能在更短的时间内达到需求的扭矩值,且在达到工作要求后快速趋于稳定没有振荡,在突加负载后也可以提高扭矩并快速趋于稳定。

图10 转矩输出对比图Fig.10 Torque output comparison diagram
由此可得,在速度环增添模糊控制器进行补偿PI 参数,对系统控制有着更高的响应速度,系统的跟随性能和稳定性较好,可以满足车辆转向时对转向电机的需求。
4.3 三闭环控制建模及试验分析
图11 是三闭环矢量控制图。三闭环矢量控制模型由信号输入模块、P 加前馈控制模块、速度环模块、位置环模块、SVPWM模块以及永磁同步电机模块组成。该模型分别以阶跃响应和正弦响应信号作为输入,模拟车辆在转向过程中可能遇到的一些工况。永磁同步电机采用matlab 中自带的永磁同步电机模型。
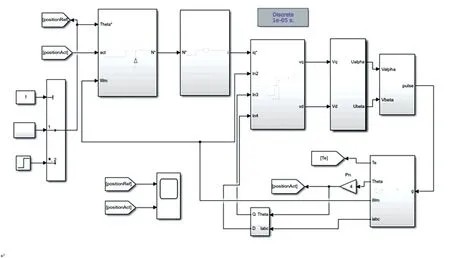
图11 三闭环矢量控制模型图Fig.11 Three closed-loop vector control model diagram
4.3.1 阶跃响应
当K=200 时阶跃响应的位置波形如图12 所示。

图12 阶跃响应角度跟随图Fig.12 Step response Angle follows diagram
从图中可以看出,控制系统的输出可以在0.05 s内跟随给定的位置而且不存在超调。系统跟随性能和快速性能较好,能够满足驾驶员在给方向盘突加转角时,车辆对转向电机的需求,可以很好的跟随控制。
4.3.2 正弦响应
当K=750 时正弦响应的位置波形如图13 所示。其中,蓝色曲线是预设角度,红色曲线是实际控制的角度输出。从图中可以看出,系统的位置输出能够时刻保持对给定信号的跟随,相对于给定信号滞后程度微小。系统跟随性能和快速性能较为良好,可以满足实际应用的需求。

图13 正弦响应角度跟随图Fig.13 Sinusoidal response angles follow the graph
5 结束语
本文基于simulink 搭建了永磁同步电机三闭环矢量控制模型,并通过对系统输入阶跃信号和正弦信号来模拟驾驶过程中驾驶员对电机转向的需求,具有很好的跟随效果。通过对比传统PI 控制,得出在速度环增添模糊控制器可以获得更高的响应速度和稳定性,为后续对线控转向系统的研究提供了理论依据和基础。
