考虑路面状态的车辆纵向避障控制策略研究

2022-03-01张晓斐王孝兰郭晨

智能计算机与应用 2022年1期

张晓斐，王孝兰，郭晨

（上海工程技术大学，机械与汽车工程学院，上海 201620）

0 引言

近年来，众多主动安全技术得到各汽车行业和各国学者的广泛关注。特别是汽车AEB（Autonomous Emergency Break自动紧急制动）系统，该系统能在事故发生前降低事故的发生率和事故导致的受伤率。

智能车辆避障系统通过车载传感器如毫米波雷达等，收集环境信息，建立安全距离模型，通过辨识路面状态，搭建整体的避障系统。目前避障控制策略的研究主要基于传统安全距离模型进行参数改进，没有考虑复杂的行驶环境因素，未考虑路面条件的影响，路面附着系数通常被设为常量，算法只能在某种特定路面获得较好的预警效果。

路面附着系数估计算法有两类：Model-based 算法，以固定的数学模型为基础计算附着系数；Experiment-based 算法主要应用车载传感器进行测量，进而完成附着系数计算。

在国内路面状态的研究上，文献［4］针对不同的附着系数道路，采取不同的混合理论估计方法；文献［5］以杜戈夫轮胎模型为基础，利用BP 神经网络对路面状态进行估计，得出了可观的结果；文献［6］分别对不同附着系数的道路建立不同的估计模型，来解决估计过程中出现较大波动的问题；文献［7］利用现有的Burckhardt 轮胎-路面数学模型，实现了路面识别；文献［8］以Pacejka 及LuGre 轮胎模型为基础，采用递归非线性的方法成功区分了不同类型的路面。

本文分析了路面附着系数对纵向避障制动效能的影响，基于滑移率与路面附着系数的关系，采用最小二乘法拟合设计路面附着系数估计算法，以保证对路面附着系数进行精确识别，建立了基于路面附着系数估计的安全距离模型，讨论了安全性要求和舒适性要求对避障控制的影响。在此基础上，建立基于MPC的汽车纵向避障控制策略，并选取典型工况进行Matlab ／Simulink-PreScan 联合仿真，验证算法的控制效果。

1 安全距离建模

1.1 制动过程

汽车制动过程中制动减速度的变化曲线如图1所示。

图1 车辆制动过程制动减速度变化图Fig.1 Change of braking deceleration during vehicle braking

为驾驶员的反应时间；为制动间隙时间；为车辆产生制动到达到最大制动力所经过的时间；为持续制动时间，此时减速度达到最大，直到制动结束。

以下公式中，表示车辆初始车速；为最大加速度，该值为μg；表示路面附着系数；表示重力加速度，大小为9.81 m／s。

水平路面车辆制动过程中，考虑路面附着情况不同带来的最大减速度不同。阶段一汽车的行驶距离为式（1）：

此过程初速度为的匀速运动。

阶段二行驶的距离为式（2）：

此过程也是初速度为的匀速运动。

阶段三时间与速度的关系表示为式（3）：

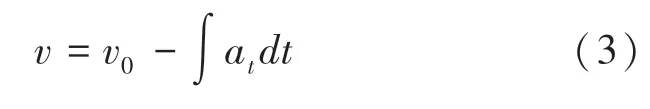
其中，为该阶段初速度， a为时刻的加速度。

速度与距离之间的关系为式（4）：

将式（3）和式（4）结合得到式（5）：

此过程是加速度增大的减速运动，为减速度的最大值。

阶段四为持续制动阶段，减速度不变，初速度为阶段三的末速度，即式（6）：

此过程为加速度不变的持续制动运动，直至车辆静止。结合运动学公式，本阶段的行驶距离为式（7）：

式（6）与式（7）结合得到本阶段的行驶距离为式（8）：

得到汽车的制动总距离公式（9）：

1.2 路面估计

路面与轮胎之间的摩擦力由式（11）计算：

其中，F为切向反力的极限值。

路面附着系数的大小与路面类型有很大的关系，各种路面上的平均附着系数数值见表1。驾驶速度和车轮运动也会影响路面的附着能力，附着系数由路面和轮胎决定，其值显示出高度可变的摩擦性能。滑移率可用式（12）计算：

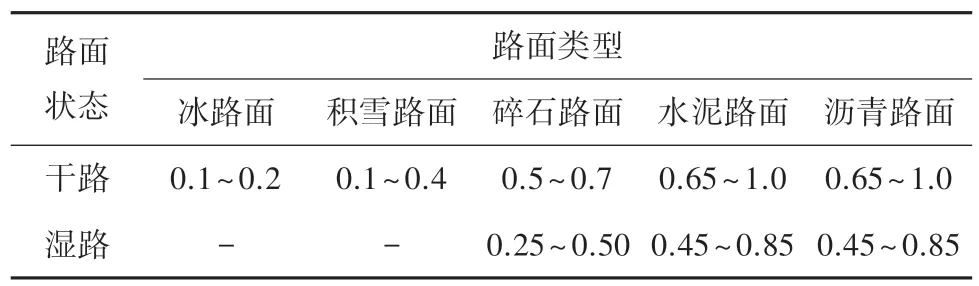
表1 各种路面的平均附着系数Tab.1 Average adhesion coefficient on various roads

其中，ω为车轮转速。

根据上述关系，车辆运行状态可分为：线性区域（该区域的滑移率满足0 ≤005）和饱和区域（该区域的滑移率满足005 ≤03）。车轮正常行驶时轮速约等于车速，滑移率一般小于0.05；当车辆加速或紧急制动时，车辆状态迅速从线性区域过渡到饱和区域，其间存在的过渡区域可以忽略不计。因此，可以在车辆制动前只考虑线性区域的求解问题。

汽车在PreScan模拟环境下计算的滑移率如图2 所示。从图中数值可以看出，滑移率很小，通常小于0.05。

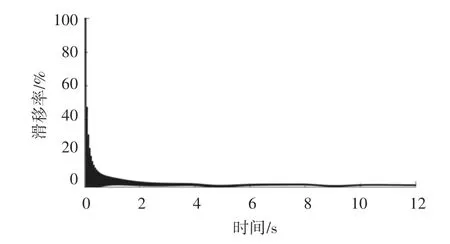
图2 车辆滑移率Fig.2 Vehicle slip rate

结合滚动阻力系数，利用滑移率与附着系数的关系来判断路面的状况。

设左前轮和右前轮的垂直载荷相等，左后轮和右后轮的垂直载荷相等，即式（13）和式（14）：

汽车在某些道路上以中低速行驶时，滚动摩擦系数的近似值见表2。

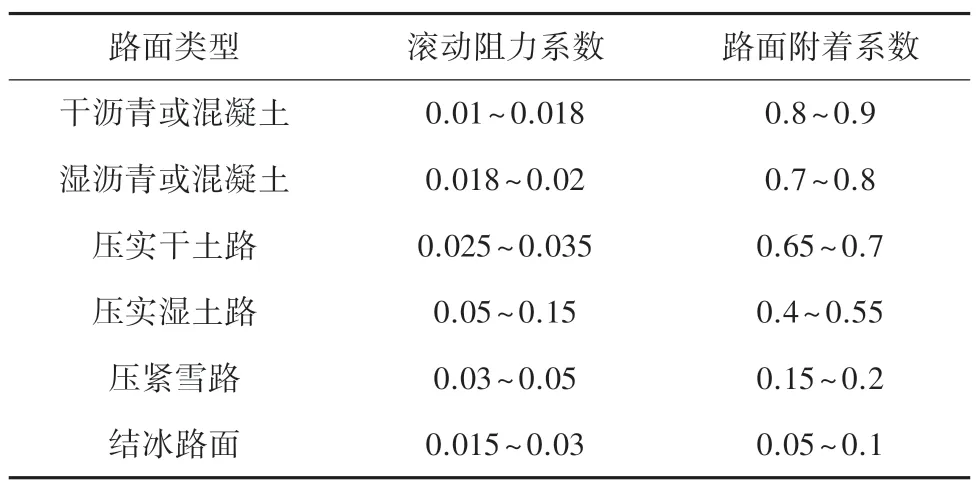
表2 不同路面滚动摩擦系数和附着系数值Tab.2 The rolling friction coefficient and adhesion coefficient of different pavement

滚动阻力系数可由式（15）～式（17）计算：

结合式（12）～式（18）采用最小二乘法进行多元拟合，得到了滚动阻力系数与路面附着系数的关系，式（18）：

通过对轮胎的滚动阻力系数估计来对路面状况进行反馈。为证明算法的可靠性和准确度，利用仿真软件将路面的附着系数设为0.5，车辆速度为36 km／h，仿真结果如图3 所示。

图3 传统与改进附着系数估计结果对比Fig.3 The results of traditional and improved attachment coefficient estimation algorithm

由图3 可以看出，相比传统的估计算法，改进后的检测算法较早达到收敛条件，整体波动范围和局部波动范围较小；同时，改进后的平均误差为0.007 31，小于改进前的平均误差0.021 07，准确率为98.63%。

1.3 基于路面状态的安全距离模型

安全距离模型被众多因素所影响，包括自车车速、前车车速、驾驶员反应时间、制动间隙和制动减速度。这些因素对安全距离模型的建立起到了关键性的作用，路面附着状态变化会严重影响到车辆制动时的减速度的大小，进而影响到车辆的制动距离。

整个制动过程自车和前车之间的距离关系如图4 所示，则传统的安全距离可以表述为式（19）：

图4 制动过程中距离变化图Fig.4 Distance change diagram during braking process

其中， S为安全距离；为汽车制动过程中行驶的距离；S为前车行驶的距离；为正常驻车时所需要的安全距离。

建立不同工况下的安全距离模型：

（1）前车静止，式（12）：

（2）前车匀速，式（21）：

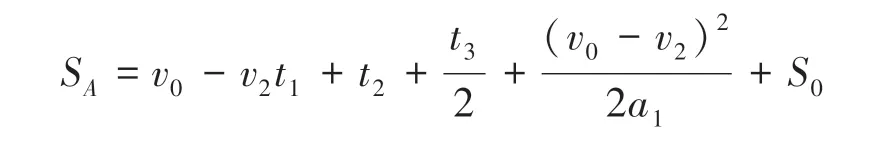
（3）前车减速，式（22）：

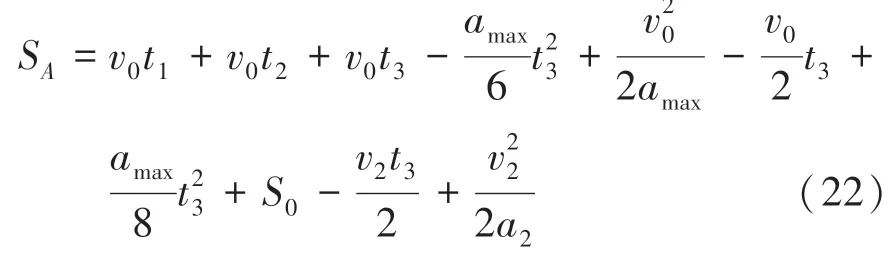
考虑路面附着系数的安全距离三维图如图5 所示，车速80 km／h 时得到的考虑路面附着系数与否的安全距离数值对比结果见表3。容易得出，改进后的安全距离模型随着道路因素的变化而变化，该模型在不同因素下能较好地计算安全距离，具有较好的动态适应性。

图5 不同速度下考虑路面附着系数的安全距离三维图Fig.5 Three-dimensional safety distance diagram considering road adhesion coefficient at different speeds

表3 80 km／h 时有无路面附着系数安全距离数值比较Tab.3 Numerical comparison of safety distance without road adhesion coefficient at 80 km／h

2 纵向避障控制策略的设计

采用分层控制结构，上层控制器获得环境参数和车辆状态参数，输出期望加速度作为下层控制器的输入；下层控制器根据输入确定节气门开度和制动压力，使得实际加速度能够跟踪期望加速度，从而实现分层控制。基于PID 算法设计下层控制策略，并建立逆动力学模型。

上层控制器需要完成针对多目标的约束优化，因此在MPC 理论框架的基础上进行预测、滚动优化和反馈校正。在约束条件的设计中，融入安全性和舒适性因素，从而实现控制要求。

2.1 状态空间方程

将两车间距（），本车车速v（），两车相对速度v（），本车加速度a（）统一到汽车纵向运动模型中，建立运动学模型（23）。

（）为第时刻的期望加速度；（）为系统干扰量；（）为目标车辆加速度；为系统的采样时间；为控制时间常数。

为同时满足车辆的避障特性和对驾驶员的保护性能，选取车间距离，本车速度和本车加速度作为优化性能指标，系统的输出方程为式（24）：

根据式（23）和式（24）可得到状态空间模型，式（25）：

2.2 目标函数及约束条件

评价纵向乘坐舒适性指标主要分析纵向加速度和加速度变化率，在现实生活中还需要考虑乘员舒适性。因此车辆在保证安全的同时，加速度变化量应在尽可能小的范围，保证乘员的舒适度。舒适度可分为4 种情况，具体如下：

（1）正常强度制动（舒适度：一般）：制动减速度绝对值小于3 m／s；

（2）小强度制动（舒适度：稍感不适）：减速度范围在-6～-3 m／s内，对人员造成了轻微不适感；

（3）中强度制动（舒适度：非常不适）：减速度范围在-8～-6 m／s内，车内乘客舒适感极低；

（4）高强度制动（舒适度：极不舒适）：加速度已经大于8 m／s，乘员无任何舒适性。

所以，将期望加速度变化量（）作为第一控制目标，设计目标函数第一项为式（26）：

其中，Γ为权重系数组成的对角矩阵。

将推测量与期望参考量之间的误差值作为第二控制目标，因此目标函数第二项为式（27）：

其中，y（）为期望参考量。

由式（26）和式（27）得到目标函数，式（28）：

通常情况下，需要对车辆进行碰撞安全的计算，以对当前车辆的安全性做出评价。其中，的计算公式（29）为：

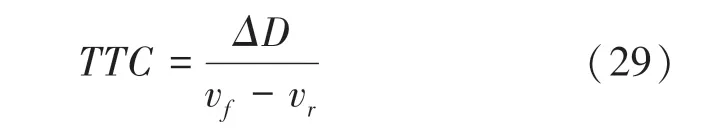
其中，为相对距离；v为前车车速；v为后车车速；v-v代表前车与后车的速度差，即Δv＝v-v。

纵向避障控制系统要保证的目标是两车的安全距离。为避免碰撞，需要对车距进行限制，式（30）：

其中，d为自车与目标车辆的实际车间距，即安全距离。

采用TTC 策略来描述安全临界距离和速度误差之间的关系，约束条件可以表示为式（31）：

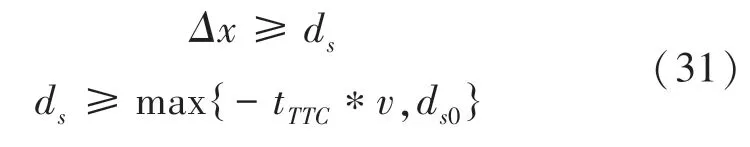
其中， d为本车与目标车之间的最小安全距离，即安全临界距离。

对v、a、以及期望加速度变化量进行约束限制：

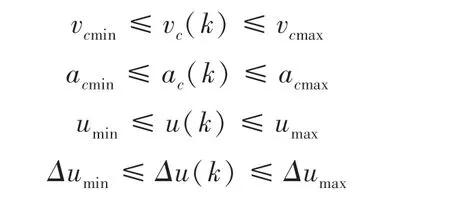
其中， v、v、a、a、、、和分别为v、a、以及的最小值和最大值。

综合以上各式建立如图6 所示的纵向避障控制策略，根据自车周围环境，在纵向方向上做出加速、跟驰或制动的决策。上层MPC 控制模块将决策信息转化为下层逆动力学控制模块可识别的参数，下层控制器再将其转化为制动、加速或跟驰等动作。

图6 纵向避障控制策略结构图Fig.6 Structure of Longitudinal Obstacle Avoidance Control Strategy

上层MPC 控制器的输出即控制量为自车的期望加速度，参考量为期望安全车间距和目标车辆的速度，输入量即预测量为自车速度和加速度、两车相对速度、以及真实的两车距离，干扰量为目标车辆加速度。下层逆动力学控制器的输出为节气门开度和制动踏板压力，输入为期望加速度。

3 联合仿真验证和分析

利用MATLAB／Simulink-PreScan 搭建联合仿真场景。

工况一：本车以60 km／h 做匀速行驶，障碍车静止，车距100 m，结果如图7 所示。

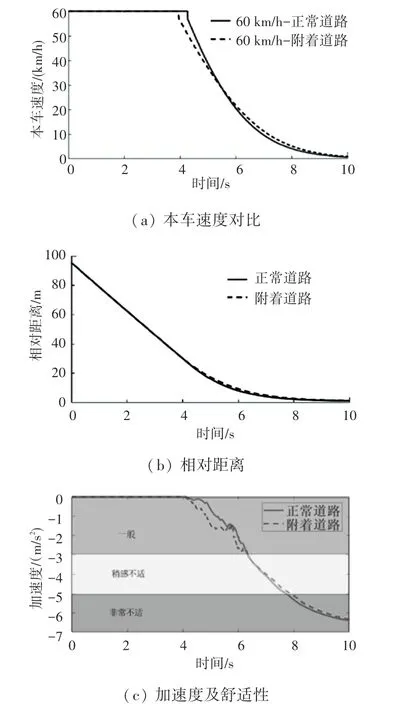
图7 自车速度60 km／h 时前车静止工况仿真结果Fig.7 Simulation results of static condition of the leading vehicle when speed is 60 km／h

初始阶段相对安全，本车保持匀速。随着距离的缩短，碰撞风险逐渐加大，此时开始制动，相对速度和相对距离持续减小，在第10 s 时刻速度为0，与前车的距离也达到最小值2.36 m，成功实现避障。此过程驾驶员的主观感受先后经过了一般、稍感不适到非常不适，在驾驶员能够忍受的舒适性范围内车辆能够成功实现避障，证明了算法的有效性。

工况二：两车相距80 m，前车以20 km／h 速度前行，本车车速60 km／h，结果如图8 所示。

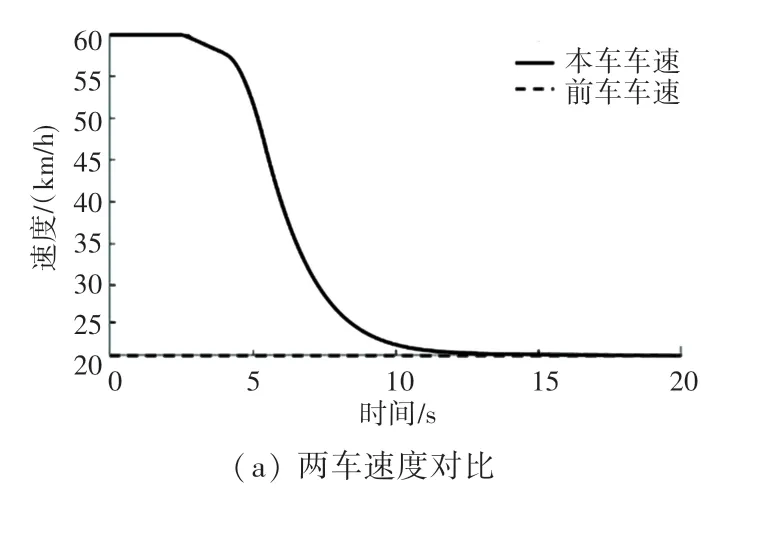
图8 自车速度为60 km／h 时的前车匀速工况仿真结果Fig.8 Simulation results of uniform speed of the leading vehicle when speed is 60 km／h

本车匀速行驶，碰撞风险较小。在5 s 左右车辆所需安全距离大于相对距离，为2.42 s。控制器开始工作，自车迅速减速，并持续了5 s 左右。12 s时刻左右，自车车速已经降至20 km／h，此后稳定跟车行驶，与前车相距7.5 m 左右。此过程驾驶员的主观感受由一般过度到稍感不适，保证了较好的乘员舒适性，车辆成功实现避障，证明了算法的有效性。

工况三：本车车速80 km／h，前车速度60 km／h且车距60 m，前车以3 m／s的减速度制动，结果如图9 所示。

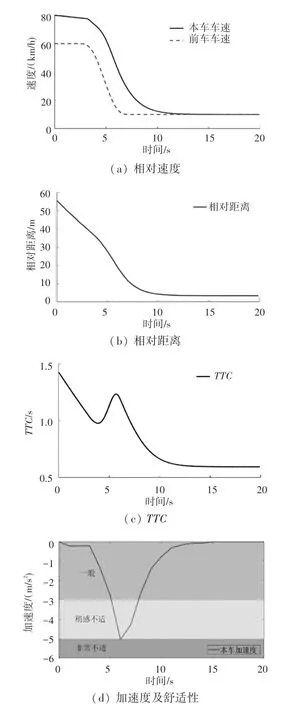
图9 自车速度为80 km／h 时的前车减速工况仿真结果Fig.9 Simulation results of deceleration condition of the leading vehicle when speed is 80 km／h

随着车距缩短，不断减小到1.5 s 左右。前车开始制动后，速度迅速下降，车距进一步缩小，相对速度增加，值迅速下降到0.6 s。随着距离减小，车距达到安全距离，车辆开始制动，同时碰撞风险逐渐增大，最终车辆实现稳定跟车，此时车距5.84 m。在制动过程中，驾驶员的乘坐舒适性由一般到稍感不适，保证了较好的舒适性，且成功实现避障，证明了算法的有效性。