一种基于中频滤波的动态步长聚焦算法

梁 鑫，卿粼波，要小涛，何海波

（1 四川大学 电子信息学院，成都 610065；2 成都西图科技有限公司，成都 610014）

0 引言

在石油地质勘探中，通过将钻井中取出的岩石制作成岩石薄片，再对岩石薄片进行分析就可得出石油的含量情况。在岩石薄片图像采集过程中，对岩石薄片聚焦清晰度的评判将直接影响后续图像拼接和图像的分析结果。由于手动聚焦耗费大量的人力物力，因此对岩石薄片图像采集使用自动聚焦的方法。

自动聚焦可分为主动聚焦和被动聚焦两种方式。主动聚焦是通过调整光学仪器测量镜头和待测物体之间的距离，来达到聚焦的目的；被动聚焦则是通过图像处理算法，来评价当前焦平面的清晰度，通过移动载物台获取清晰度评价最好的焦平面。主动聚焦对光学仪器的精度要求较高，实现起来有一定难度，因此被动聚焦的应用范围更加广泛。

对于不同的应用场景，自动聚焦有着不同的技术难题。对于被动式的岩石薄片自动聚焦问题，主要存在清晰度评价函数和聚焦搜索两方面的问题。对此，国内外学者提出了各自的解决方案。文献［3］针对采集的图片分辨率高、计算量大的问题，根据图像灰度特点提出了灰度非0值统计函数和低灰度值统计函数的聚焦算法；文献［4］对低倍率显微图像中的细胞定位，提出了基于八邻域算子和最小二乘平面拟合的自动聚焦算法；文献［5］中针对高分辨率下的中期染色体聚焦算法；文献［6］中提出的针对视频监控和跟踪系统的自动对焦算法等等。另外，学者们还针对相应的应用场景，提出了不同的聚焦区域选择算法。其中，由于细胞薄片的感兴趣区域分布不均匀，文献［7-8］分别就人工鱼群算法进行改进，以获取合适的聚焦窗口；文献［9］就运动检测获取感兴趣区域，再对这个区域选择合适的焦窗，在连续图像中对该窗口进行跟踪；文献［10］就图像的熵和边缘信息选择最优的点扩散函数获取聚焦区域；文献［11］中，为高效的获取聚焦平面，提出了混合搜索法来提高搜索效率。

在岩石薄片图像的采集中，由于岩石薄片中不同矿物本身的岩性不同，以及岩石薄片的制作工艺等问题，容易引进一些噪声。传统的聚焦评价函数若直接用于对岩石显微图像的评价，评价结果的准确性往往不够理想，需要进行改进。本文就岩石薄片的特性，在聚焦评价之前，对岩石显微图像做了预处理，再通过实验选出最优的聚焦评价函数，并与常见的聚焦评价函数做了定标的对比。在聚焦区域方面，由于岩石薄片在90%以上的区域都有丰富的图像信息，因此本文选择对整个视场进行聚焦评价。同时，为了更有效和准确的获取到聚焦平面，提出了一种动态步长焦平面的聚焦搜索策略。实验结果表明，本文提出的聚焦评价方法和聚焦搜索算法均有较高的可靠性和稳定性。

1 传统聚焦函数及评价指标

聚焦评价函数是整个聚焦过程中最重要的一环，一个好的聚焦评价函数不仅影响图像清晰度的判定，还会对后续的聚焦搜索造成影响。本文的聚焦过程是通过聚焦函数，计算出当前焦平面的清晰度的值，通过上下移动载物台找到清晰度值最大的焦平面，此焦平面即为聚焦平面。

1.1 聚焦评价函数

根据图像的细节分布规律，图像的细节越多，纹理越清楚，图像也就越清晰。从梯度值变化的角度来看，图像的梯度值越大图像越清晰；从频域的角度来看，图像的细节主要是由高频份量来体现，图像的高频分量越多，图像细节越丰富，图像也就越清晰。由于频域的计算量较大，聚焦效率低，所以一般常用的聚焦函数是通过计算图像的梯度来评价图像的清晰度，常见的聚焦评价函数如下：

（1）Tenengrad 函数

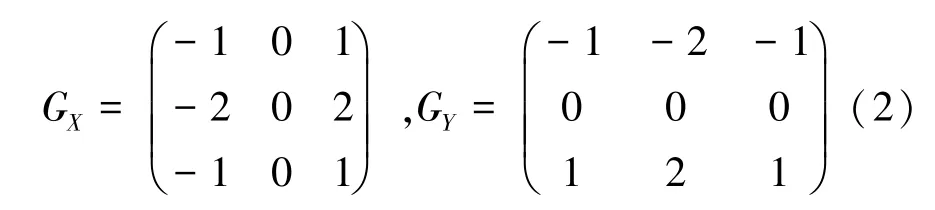
其中，C与C是图像分别与卷积算子G和G卷积后的结果，和是图像的大小。

（2）Brenner 函数

其中，（，）是图像的灰度值。

（3）Energy 函数

（4）Laplacian 函数

其中，（，）是图像与Laplacian 算子（式（6））卷积后的结果。

1.2 聚焦函数评价指标

为了定标的衡量聚焦函数的好坏，采用陡峭区宽度、清晰度比率、陡峭度、平滑区波动量和灵敏度，从不同角度反应聚焦函数的性能。

（1）陡峭区宽度W。是根据聚焦曲线的特点将聚焦曲线分为平缓区和陡峭区。当聚焦函数和图像内容确定时，聚焦曲线的平缓区和陡峭区也就确定了。用z表示左平缓到左陡峭区的临界点； z表示右陡峭区到右平缓区的临界点；W为二者差的绝对值，如式（7）所示。

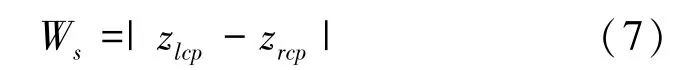
（2）清晰度比率。是聚焦评价函数最大值与最小值的比值，表征了聚焦函数对不同离焦程度图像的分辨能力，如式（8）所示。

（3）陡峭度。反映聚焦函数对不同距离焦程度图像的分辨能力，还可以表征聚焦曲线的形态。对于不同的聚焦函数，值越大，聚焦曲线越陡峭，对图像的离焦分辨能力越高。其表达如式（9）所示。

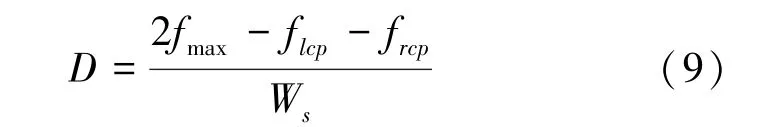
其中，f为聚焦评价函数起点函数值，f为聚焦评价函数终点函数值。

（4）平滑区波动量V。反映聚焦函数的抗噪声性能。V的值越大，表明聚焦曲线平缓区波动大，聚焦函数的抗噪声性能越差。V的计算方式如式（10）所示。

（5）灵敏度D。用来表征聚焦函数最大值附近的变化程度。灵敏度越高的聚焦函数，在其最大值附近变化越明显，越容易找到聚焦最好的焦平面其表达形式如式（11）。

其中，（）是最大值处的横坐标移动处的聚焦函数值。

2 传统聚焦搜索算法

通过聚焦函数可以计算出当前焦平面的函数值，但如果对每个焦平面都做一次计算，再从这些结果中选出最大值，效率较低，且由于拍摄环境光照影响，采集设备中图像传感器长期工作产生的热噪声及载物台电机运动的不平稳等因素，会在聚焦评价值计算的过程中产生一些局部极值。从聚焦评价曲线来看（如图1 所示），会产生一些小的单峰，容易将这些局部极值点作为最终的聚焦平面。因此，需要通过一些聚焦搜索策略来减少这种误判。常见的搜索算法有爬山搜索算法、两阶段搜索算法等。

图1 具有局部极值的聚焦评价曲线Fig.1 Focus evaluation curve with local extremum

2.1 爬山搜索算法

爬山搜索算法是通过一定的步长和方向移动载物台的轴实现的。在搜索开始时，计算当前焦平面的聚焦函数值，再以任意方向移动载物台的轴后，计算移动后焦平面的聚焦函数值。通过比较两次的值，确定下一次的移动方向，直至找到最大的聚焦函数值所在的焦平面。

虽然爬山搜索算法较为简单，但对聚焦函数要求较高，若采集过程出现局部极值的问题，其算法容易将局部极值所在焦平面作为最终的聚焦平面。

2.2 两阶段搜索算法

两阶段搜索算法是以爬山搜索算法为基础提出的，在其算法中增加了步长参数：大步长L和小步长L。在粗搜索阶段，使用大步长L可以快速定位到聚焦评价曲线的峰值位置，而小步长L用于反向精细搜索阶段。根据设定的阈值，在上次的聚焦函数评价值与当前聚焦函数评价值绝对值之差小于阈值时，则停止搜索。

两阶段搜索算法虽然在搜索效率上有所提高，但还是会陷入局部极值点，并且粗搜索和精细搜索的步长也要根据实际应用情况做相应调整。

3 聚焦函数及聚焦搜索算法

3.1 基于中频滤波的Laplacian 聚焦函数

从图像的频域来看，主要分为低频、中频和高频，这3个频段所呈现的图像信息各有特点，图像的低频信息，主要是图像的灰度等级信息，是图像的基础属性；图像的中频信息，是图像的主要边缘结构，决定了图像的基本结构；图像的高频信息，是图像的细节，主要是在中频信息上对图像内容的进一步强化。根据岩石薄片的特点，用图像的结构信息更符合作为聚焦评价依据。因此，本文先采用中频离散余弦变换（Medium Frequency Discrete Cosine Transform，MFDCT）对图像进行预处理。MFDCT对脉冲噪声和高斯噪声有很好的鲁棒性，可以滤除图像的高频信息和低频信息，保留中频信息。其卷积算子如式（12）所示。

将原始图像（，）与卷积算子K进行卷积运算，即可得到待评价的新图像（，）。计算如式（13）。

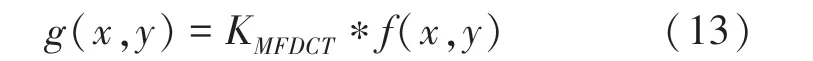
如图2 所示，图2（a）～（d）是从模糊到清晰的岩石薄片图像，随着图像从模糊到清晰，图像对应的中频图像展示的图像结构也越清晰。之后，再采用Laplacian 函数作为聚焦评价函数，来计算新图像（，）的聚焦评价值。

图2 不同焦平面岩石薄片图像及中频信息Fig.2 Rock slice images and intermediate frequency information of different focal planes

3.2 动态步长搜索算法

爬山搜索算法与两阶段搜索算法由于对步长设定的局限，对局部极值均有不同程度的敏感，特别是在岩石薄片显微图像中，由于岩石薄片中不同岩石特性不同，无法做到绝对的平整，在采集过程中容易出现局部极值点。对此，本文提出一种动态步长的搜索算法，算法实现步骤如下：

使用步长作为初始搜索步长向后搜索，且每移动一个步长计算一次焦平面的聚焦函数值，记作F。同时比较当前焦平面聚焦函数值F与上一个焦平面聚焦函数值F，若出现F ＜F，则向后搜索步。值计算如式（14）所示。

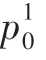
则下一次的搜索区域为［M-D／2，M +D／2］，同时按式（16）更新下一次的搜索步长L后，再次执行步骤（1）。

计算聚焦函数绝对值之差，如式（17）所示。

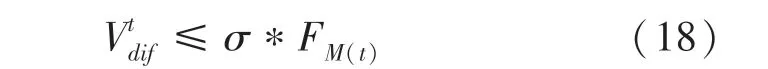
式中，是判断搜索结束的系数。

4 实验分析

本文采用基于蔡司显微镜开发的岩石薄片显微图像采集系统；载物台具有3个移动方向，其中包括视场的前后左右移动以及聚焦过程中的上下移动。实验使用的岩石薄片显微图像数据，是以固定步长采集的离焦到聚焦再到离焦的图像序列，如图3 所示：

图3 离焦-聚焦-离焦序列图Fig.3 Defocus-focus-defocus sequence diagram

将样本1 与样本2 分别使用Tenengrad 函数、Brenner 函数、Energy 函数、Laplacian 函数以及本文的基于中频滤波的Laplacian 函数计算评价值，并将计算得到的评价值归一化后得到如图4 所示的聚焦评价曲线。

图4 不同样本的聚焦函数归一化曲线Fig.4 Normalized curve of focus function for different samples

将样本1 与样本2 得到的聚焦函数曲线，通过计算评价指标得到结果见表1、表2：

表1 样本1 评价指标Tab.1 Evaluation Index of Sample 1

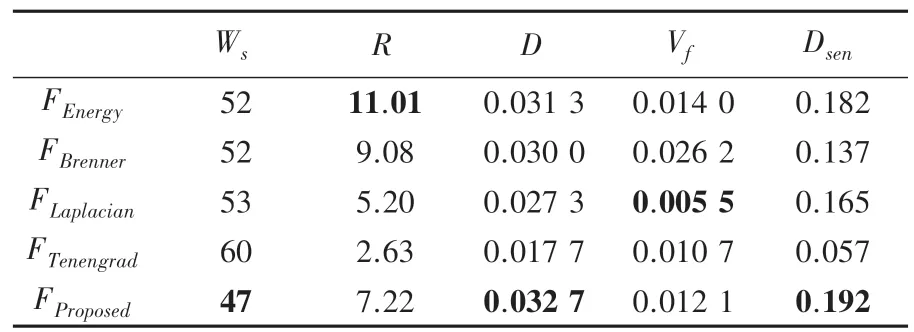
表2 样本2 评价指标Tab.2 Evaluation Index of Sample 2

从图4和表1、表2的数据来看，Tenengrad 函数和Brenner 函数均有较大的陡峭区宽度，本文先通过中频滤波算子滤除图像的高频和低频信息，保留了图像的框架信息，再通过Laplacian 函数计算图像的聚焦评价值，有效降低了陡峭区宽度，增加了陡峭度并提升了灵敏度，为后续的搜索算法奠定了基础。

对于样本3 使用两阶段搜索法和动态步长搜索法，结果如图5 所示。

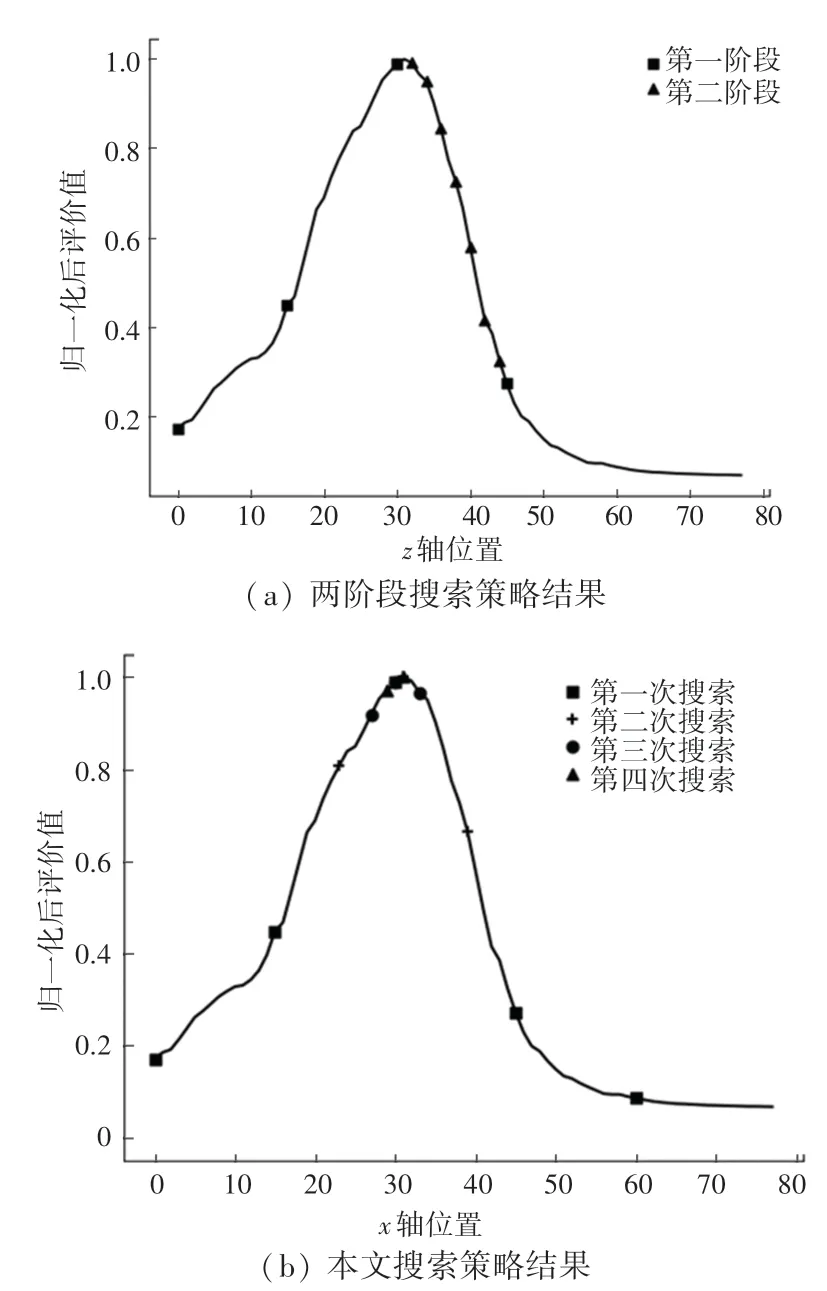
图5 样本3不同搜索方法结果对比Fig.5 Sample 3 Comparison of results of different search methods

从图5（a）中可以看出，两阶段搜索法先通过大步长搜索，在出现清晰度评价值下降的情况时，以小步长进行搜索。但由于步长的选择问题，最终以最佳聚焦平面附近的聚焦平面作为最终的搜索结果，导致结果不准确。而从图5（b）中可以看出，本文的动态步长搜索算法先是以一个初始步长进行搜索，在其后的搜索过程中动态调整步长和搜索区域，最终找到最佳的聚焦平面。

为验证本文动态步长搜索算法在具有非脉冲型局部极值图像序列的优越性，将样本2 中的部分图像引入高斯噪声，形成非脉冲型的局部极值作为样本4。图6 是对样本4 进行两阶段搜索和动态步长搜索的结果。

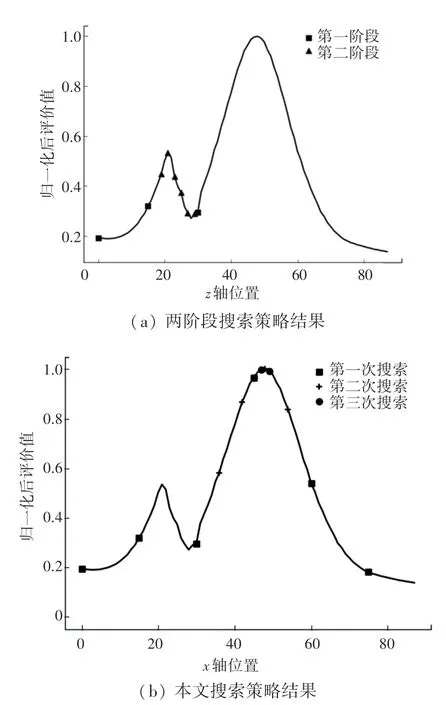
图6 样本4不同搜索算法结果对比Fig.6 Sample 4 Comparison of results of different search methods

从图6 中可以看出，两阶段搜索策略在搜索过程中依赖于搜索步长的选择，导致对于局部极值过于敏感，最终将非脉冲型局部极值当作了最大值，搜索到了错误的聚焦平面；而本文提出的搜索策略，根据已搜索的位置点的数量及搜索出的清晰度值，计算出继续向后搜索的距离，并动态更新搜索区域和搜索步长减弱了非脉冲型局部极值的影响，成功地找到了最大值的位置，即最佳聚焦平面，验证了本文算法的有效性与可靠性。

5 结束语

本文提出的基于中频滤波和Laplacian 函数结合的聚焦评价方法及动态步长聚焦搜索算法，通过先将图像经中频滤波算子预处理，滤除高频和低频信息，保留图像的基本结构，再通过Laplacian 函数计算图像聚焦评价值，有效的减小了陡峭区宽度，增加了灵敏度，使找到最佳聚焦平面更容易。此外，动态步长搜索算法记录每次的搜索结果，并通过这些搜索结果调整搜索区域和搜索步长，有效降低了局部极值对搜索结果的影响，并通过实验验证比较验证了本文算法的有效性。