三维模型分割的研究及其在人体测量中的应用
2022-03-01刘巧雪姚砺
万 燕,刘巧雪,姚砺
(东华大学 计算机科学与技术学院,上海 201620)
0 引言
近年来,随着计算机图形学、计算机视觉等技术的发展,各种三维扫描设备逐渐普及以及人们对个性化、多样化的消费需求的追求,三维人体测量技术已经从传统的接触式测量过渡到非接触式测量,相比于传统的人工测量的方式,三维人体非接触测量技术更加方便、准确。三维人体测量研究近几年取得了一定的成效,但是相关测量技术依然有待完善。三维人体测量技术作为服装设计、生产的主要依据,逐渐成为服装业个性化发展的关键技术,也广泛应用于电子商务领域,比如虚拟试衣技术、在线测量定制等。为了更加快速、准确的测量身体各部位的尺寸,进行三维人体模型的分割成为关键的一步。
三维网格分割的结果极大影响着三维测量结果的准确性。目前国内外对三维网格模型的分割方法也比较多,Shlafman 等人提出了一种基于K 均值聚类的算法,但需指定聚类数量;Lai 等人通过在网格模型的对偶图上随机游走,按层次聚类分割;Katz 等人提出一种分层分解算法,使用多尺度将网格顶点转换为姿态不敏感的一种表示形式,提取突出特征点并提取核心部分来进行分割;Shapira 等人提出形状直径函数(SDF:Shape Diameter Function),结合高斯混合模型对网格进行分割;近几年,利用深度学习进行三维网格分割也得到了快速发展;Hanocka 等人提出一种基于边的卷积神经网络来分割三维模型,但是只能对顶点数量较少的网格进行良好的分割。
当前三维模型分割方法多种多样,其中较为经典的是利用传统形状直径函数来分割三维模型,但存在计算量大、鲁棒性较差及对复杂的模型分割效果不好的问题。针对该问题,本文提出一种改进的分割算法,先用谱方法进行过分割预处理,基于平面度误差来合并近似平面的区域,再结合相互可见性合并过分割块,最后针对传统形状直径存在的问题,采用一种基于表面偏移的形状直径来获取最终的分割结果。基于本文分割算法,用人体模型作为输入,得到分割后的头部、躯干、左右臂和左右腿等人体部位,利用极限凸点搜索法确定某些关键点,再利用切片法结合椭圆拟合法求围度周长。实验结果表明本文分割方法效果优于现有大多三维分割算法,能够正确分割不同姿态、不同体型的人体,计算的围度尺寸也满足人体测量要求,误差在允许范围内。
1 基于表面偏移形状直径的三维网格分割算法
利用传统的形状直径进行三维分割的算法存在计算量大、分割效率低、对人体模型分割不能较好的适应等问题,本文结合谱方法作为预处理,得到大量的过分割子块,计算过分割块之间的相互可见性,合并相邻过分割块,能大体分割模型各个部位,但还存在部分分割错误的区域,为了重新合并不正确的分割区域,更好的分割复杂模型,本文利用一种改进的基于表面偏移的形状直径来进行最后的合并分割,算法流程如图1 所示。
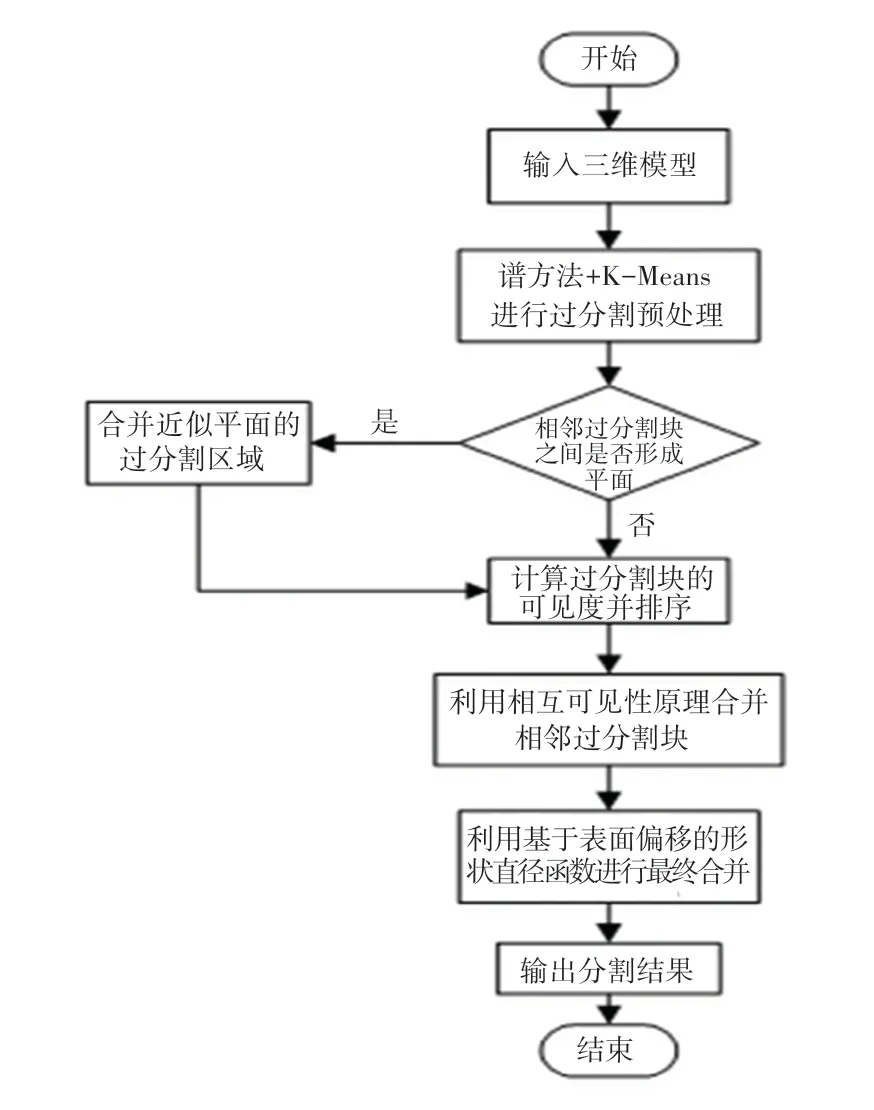
图1 基于表面偏移形状直径的三维网格分割算法Fig.1 3D mesh segmentation algorithm based on surface offset shape diameter
1.1 谱方法过分割三维网格模型
大多数传统的分割算法采用欧氏距离来表示模型上任意两个顶点之间的距离,基于此再进行后续的分割。但三维网格模型不同于二维平面图像,其存储了三维顶点、三角面片和法向量等相关信息,只用欧氏距离来表示顶点距离,会造成大量信息丢失。为了避免有效信息的丢失,本文采用网格上顶点的测地距离和角距离来共同定义网格上顶点之间的距离,这种空间距离的改进能够更好的保存三维模型的顶点位置信息,由此构造相似矩阵,再计算邻接矩阵,进而利用谱方法结合k-means 算法进行过分割。若不进行过分割,直接遍历计算每个顶点之间的相互可见性,会增大计算量,降低计算效率。本文的过分割处理使得正确的分割处都能得到分割,后续只需要对过分割的分割区域进行合并就能得到正确的分割结果。
算法步骤:




(4)K-Means 聚类:结合传统的K-Means 聚类算法对特征空间中的个特征向量进行聚类,得到个过分割块S (1,2,…,),最终可以得到并输出过分割后的三维模型,即在谱聚类后得到的大量过分割块,如图2 所示。

图2 过分割结果示意图Fig.2 Schematic diagram of over-segmentation results
本文将模型进行过分割处理,其好处是在后续的合并过程中无需遍历每个顶点及合并,极大的降低了合并的计算次数。将该步结果作为预处理结果,只需在下文利用过分割块之间的相互可见性来进一步合并过分割块。
1.2 基于相互可见性合并过分割块
谱聚类方法得到的过分割结果是不具有语义的,需要进一步合并过分割块得到更准确的分割区域。有关如何合并三维过分割块的研究较少,本文基于三维顶点的相互可见性思想来合并过分割块,得到更加符合人类视觉感知的分割结果。首先给出相互可见性和可见度的定义。
(1)相互可见性:是指三维网格模型上任意的两点p和p,当且仅当p和p所连线段完全位于网格模型内部时称网格点p和p是相互可见的,否则p和p是相互不可见的。一个三维网格模型上的两个点是相互可见的,也称这两个点位于同一个视线()中。
(2)可见度:设是一组网格模型顶点的样本点集,定义()是∈视线内的所有点对的集合,即(,) ∈()表示当且仅当网格点∈和∈是相互可见的。对于任意两个过分割块上的网格点集、⊆,将(,)表示为相互可见的点对(,),∈,∈的集合。
将一个点集的可见度等级定义为所有点对中相互可见的点对的一部分,即式(2):

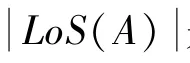
算法步骤为:
(1)合并近似平面片的相邻过分割块:为了解决无法合并近似平面的区域,本文将每个过分割块中具有相同法向量的三角形所形成的面片当作平面片,给定一个平面度误差(本文取经验值0.99),当相邻两个三角形的法向量数量积不小于时,认为该过分割块所形成的面片是平面片,合并网格模型中所有相邻的过分割平面片,通过合并平面片可以很好的解决近似平坦区域的合并问题。
(2)可见度计算:分别计算所有过分割块的可见度等级,并按顺序依次计算其与相邻过分割块之间的相互可见性。
(3)四次迭代合并:将可见度阈值设为09,08,07,0.6,这样取值在于依次放宽阈值约束条件,增加合并效率与准确度。本文增加一次迭代操作能够将分割碎片区域更好的合并到正确区域,比如合并脚部区域时会出现脚趾与脚背被分割在不同区域,此时增加一次迭代能够更好的合并脚趾部分到脚部区域。
(4)合并过分割块:当相邻过分割块S和S之间的可见度大于时,将其合并,最后得到合并后的子块{,,…,D}。过分割块已被很好的合并,但仍然存在部分区域合并不正确,比如人体脖颈被合并到躯干部分、马的腿和尾巴区域以及吉他的中心未被正确合并,如图3 所示。
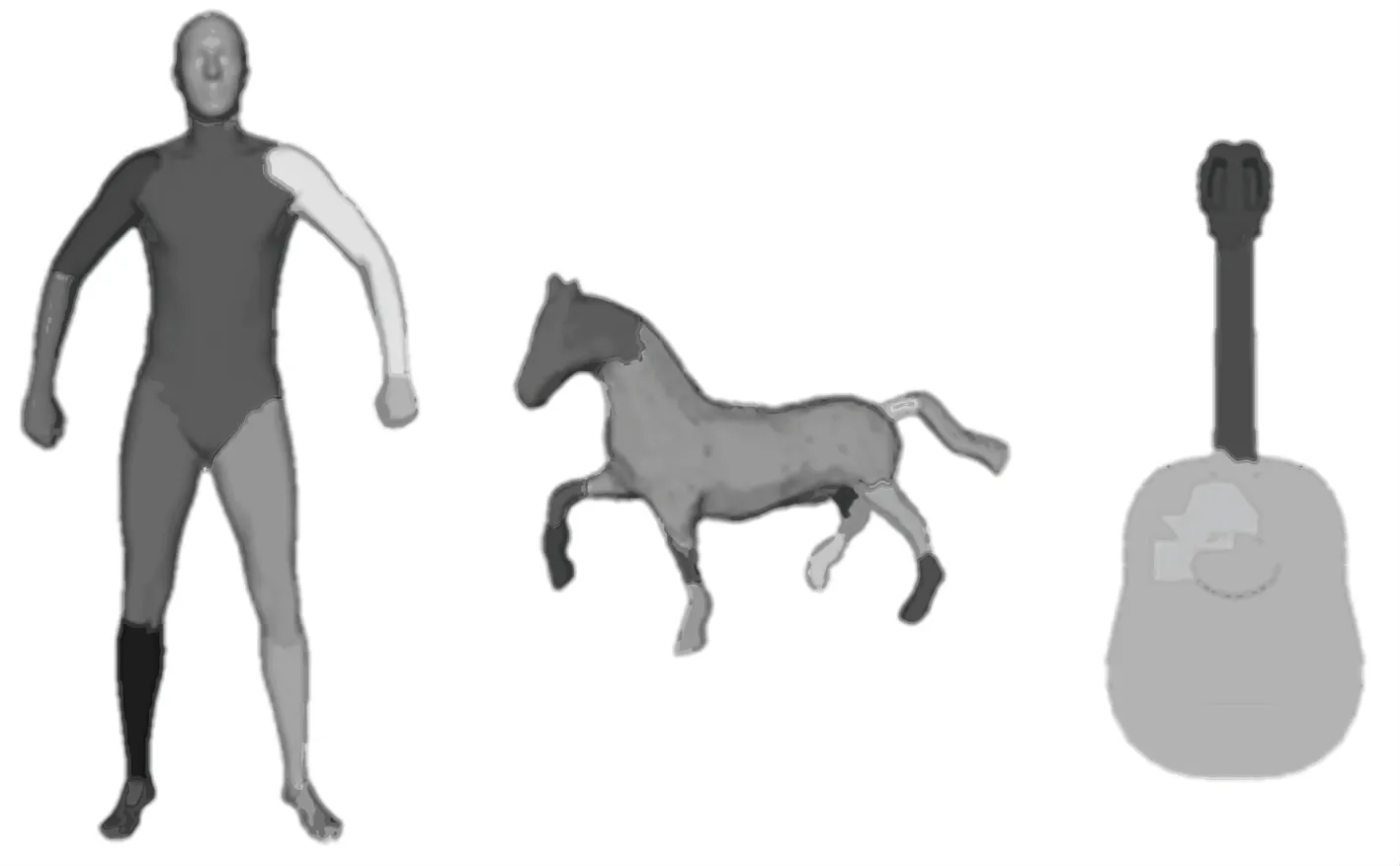
图3 过分割块合并结果Fig.3 Result of over-segmented block merging
本文继续基于表面偏移形状直径算法合并未被正确合并的区域,以进一步提高分割的合理性和准确性。
1.3 基于表面偏移形状直径函数的分割与合并
利用相互可见性进行初次合并,得到的分割结果更加符合语义,但对于更复杂多样的三维模型来说,分割效果仍然存在不足。本文提出的分割算法中最后且关键的一步是采用改进的形状直径函数来进行最终的合并分割,能较好的解决以上问题。传统的形状直径函数是在三维网格模型的顶点处放置一个倒置的圆锥,在圆锥内部发射几十条射线,一般取25 条,计算每条射线的穿透距离,取平均穿透距离作为该点的SDF值,这样的计算对网格点数量庞大的三维网格模型来说非常耗时,分割速度较慢并且对局部几何细节较敏感。针对以上问题,本文采用基于表面偏移的形状直径来改进合并结果。
基于偏移表面的SDF的定义:用表示输入的三维网格模型。对于每个顶点v,在该顶点处放置一个半径为的球体。忽略内部球体的包络,用表示所有球体的外部包络。对于网格模型上任何一个顶点∈,沿点外法线方向发送射线与相交于点,即存在一个点∈。设∈是射线和的交点,定义在处的SDF的穿透距离为‖‖2,如图4 所示。

图4 SDF 示意图Fig.4 Schematic diagram of SDF
首先设置阈值012,对于初次迭代合并得到的分割结果{,,…,D},任取相邻两个子块D和D,迭代计算子块D上所有顶点的SDF值,文献[10]通过归一化的SDF值和顶点数量构建直方图,所以本文对子块D上的所有顶点的SDF值进行归一化处理,将归一化的SDF值作为纵坐标,将子块上网格顶点数量作为横坐标,即可得到该子块的直方图h;同样方法计算得到相邻子块D的SDF 直方图h,使用相关性比较计算公式(3)和(4),计算两个直方图之间的相似度,若大于阈值,则合并D和D。迭代执行以上步骤,合并相邻区域,直到不满足条件为止,得到最终的分割结果,如图5(a)所示。从图中可以看出人体脖颈部分被正确分割到头部区域,马的四条腿和吉他中心区域均得到了准确的分割结果。与图5(b)的传统形状直径函数分割结果对比,可知本文分割效果更准确。



图5 分割结果对比Fig.5 Comparison of segmentation results
2 基于自动分割的三维人体测量技术
利用本文分割算法能够较好的分割三维人体模型各个部位,能够快速定位并测量人体围度。将分割后的人体模型身体部位分别提取出来,利用传统的切片法结合椭圆拟合法,确定关键点来计算分割后的大腿、上臂等围度,切片法结合累积距离法求胸围、腰围等围度。
2.1 基于椭圆拟合法的围度计算
通过椭圆拟合得到拟合的椭圆曲线,进而求取周长,获取围度值。椭圆拟合的关键在于将问题转换为求取特征值和特征向量,输入一组目标点的集合(x ,y),求该椭圆、、、、、6个参数,可将其简化为计算多项式(,)0,并满足约束条件40。定义向量和分别为[,,,,,],[,,,,,1],则上述多项式(,)可以记作向量F()0。对于约束条件40,当不为0 时,(≠0)代表相同的圆锥曲线,在一个合适的范围内,不等式约束条件可以转化为等式约束条件,即41。再定义一个6的矩阵和常数矩阵,如式(5)和式(6):


约束条件41 即可写成矩阵形式:1,则椭圆拟合问题转换为满足1 时,求min ‖‖,分解min ‖‖,得到min‖‖;构造拉格朗日函数:(,)(1),令其偏导数为0,如公式(7),得到0,即,令,则可得到,即式(8);最终椭圆拟合问题转为求取S特征值和特征向量的问题。

2.2 基于极限凸点搜索法的大腿围度测量
分割后的各个身体部位都存储为单独的点云数据集,其中每个点都为三维(,,) 坐标,大腿围度计算,利用极限凸点搜索法来定位大腿内侧点。大腿围是指大腿内侧肌肉最凸出处的水平周长,或经过臀股沟点处的大腿水平周长,则测量大腿围时先寻找到大腿内侧肌肉最凸出处,即图6的点。极限凸点搜索法步骤为:首先,计算出大腿最高点,设为大腿最高点所在位置,为大腿最低点所在位置,位置沿方向利用厚度为0.01的水平切面进行切割,切面与大腿模型相交,得到相交的三维轮廓点,形成的点集本文称为切面三维轮廓点集,设S为第个切面三维轮廓点集,则S为相邻的上一个切面轮廓三维点集, S为相邻的下一个切面三维轮廓点集,如式(9)~式(11):

图6 大腿内侧最凸点AFig.6 Point A on inner thigh
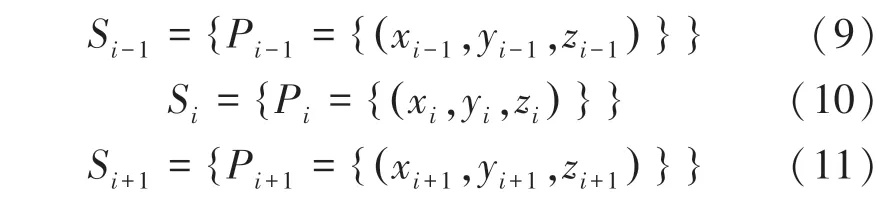
在S中同时记录轴的最大值x、最小值x和轴的最大值z和最小值z,依次与相邻上下两个切面三维轮廓点集得到的最大值进行比较,当且仅当满足式(12)时, S为经过大腿内侧最凸点所在的切面三维轮廓点集,x为大腿内侧最凸点的坐标。

将S,S,S切面三维轮廓点集投影在平面,得到二维轮廓点,如图7 所示;将经过大腿内侧最凸点的二维轮廓点集作为椭圆拟合求周长算法的输入,即可得到大腿围度值,如图8 所示。

图7 从左至右为相邻三个切面二维轮廓点Fig.7 Adjacent contour points

图8 拟合的大腿围Fig.8 Fitting thigh circumference
2.3 基于累积距离和法的腰围测量
由于体型存在差异,男女胸部形状存在差异,所以利用椭圆拟合或者凸包法求周长误差较大,本文采用累积求相邻轮廓点的距离和来计算其围度值。设二维轮廓点集中值最小和最大的两个点分别为和,连接和,所连线段将轮廓点集分为1和2 两部分,如图9 所示。线段上方的轮廓点集为1,下方的为2。对1和2 点集中的点按值大小排序,则有(,,,…,P,)∈1,(,,,…,G,)∈2,其中P(min,1,2,…,,right)和G(min,1,2,…,,right)分别表示1和2 中的点,、和、分别表示1和2 中值最小、最大的点。

图9 累积距离法示意图Fig.9 Schematic diagram of cumulative distance method
相邻两点之间距离为d,如式(13):

则1 长度为1,如式(14);同理,2 长度为2,式(15);因此围度值12。
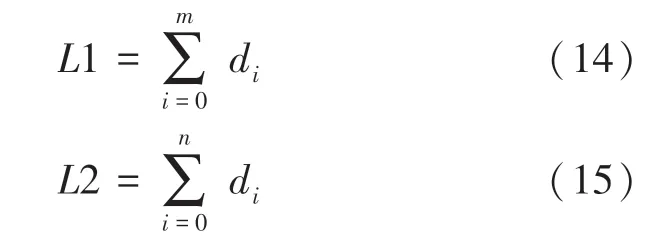
3 实验结果与分析
实验环境:本文的实验在Intel(R)Core(TM)i5-3470 CPU @ 3.20 GHz,12.0 GB 内存的window10 ×64 操作系统上进行的,代码语言为C++和matlab。
3.1 分割结果评估
本文采用普林斯顿数据集,利用4 种定量评价的基准,对本文分割结果进行评估。4 种评价指标包括分割差异(Cut Discrepancy)、汉明距离(Hamming Distance)、兰德指数(RandIndex)和一致性误差(Consistency Error)。4个评价标准都是以人类的手动分割结果作为基准,并且选取文献中提供的手工分割方法、KMeans 分割方法、LearningMesh 分割算法、ShapeDiam分割算法、CoreExtra 分割算法以及WCSeg 分割算法和SegMat分割算法进行定量对比分析,WCSeg 分割算法使用传统形状直径函数和凹凸性进行模型的分割,SegMat 分割算法是基于输入网格模型的中轴变换(MAT)来分割三维模型,可以使用相同的参数集为不同的数据集和类别生成合理的分割结果,虽然该方法分割速度相对于其他分割方法快一个数量级,但是此方法忽略了中轴提取部分的时间,其前期的中轴提取相对比较耗时。图10 中“My Paper”为本文方法的评估结果,图10(a)~图10(d)分别显示了普林斯顿数据集基于以上4 种评价指标在8 种分割方法中的评估对比结果,可以看出在4个不同的指标上,本文分割方法效果都比较好,分割结果略优于WCSeg和SegMat 方法。
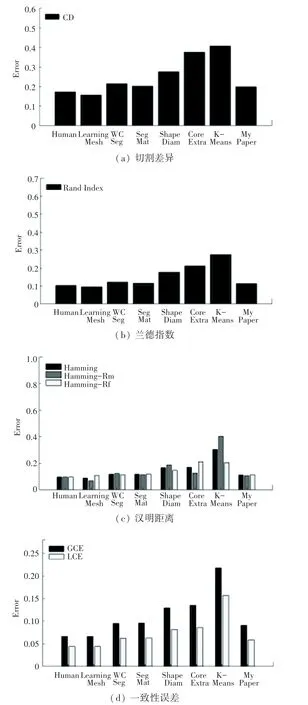
图10 本文分割效果结果评估对比Fig.10 Comparison and evaluation of segmentation results
本文利用三维网格人体模型数据库SHREC14进行人体分割实验,该人体模型数据库包含400个人体模型,其中含有40个不同的男女性模型的10种不同姿态。本文分割方法以SHEREC14 人体模型作为输入,所得到的分割结果效果,能够将三维人体模型各部位较好的分割开来,分割结果几乎不受姿势的影响,如图11 所示。

图11 人体分割效果Fig.11 Segmentation effect of human body
通过多种分割方法的对比以及4 种评价指标的评估结果,表明本文分割方法的有效性与合理性,优于大多数的分割算法;同时本文也对不同姿势的三维人体进行了分割结果对比,该分割方法不受姿态变换的影响,具有良好的鲁棒性。
3.2 人体测量结果分析
本文基于SHREC14 人体模型数据库中近似“A”字型的人体模型的分割结果来进行围度测量,包括4 组男性与女性模型。由于本文利用的是现有的完整人体模型数据库,未对真实人体进行扫描并重建,所以选择人机交互式测量软件Meshy 测量结果作为参考对比,本文人体围度测量结果与交互式软件测量结果见表1。
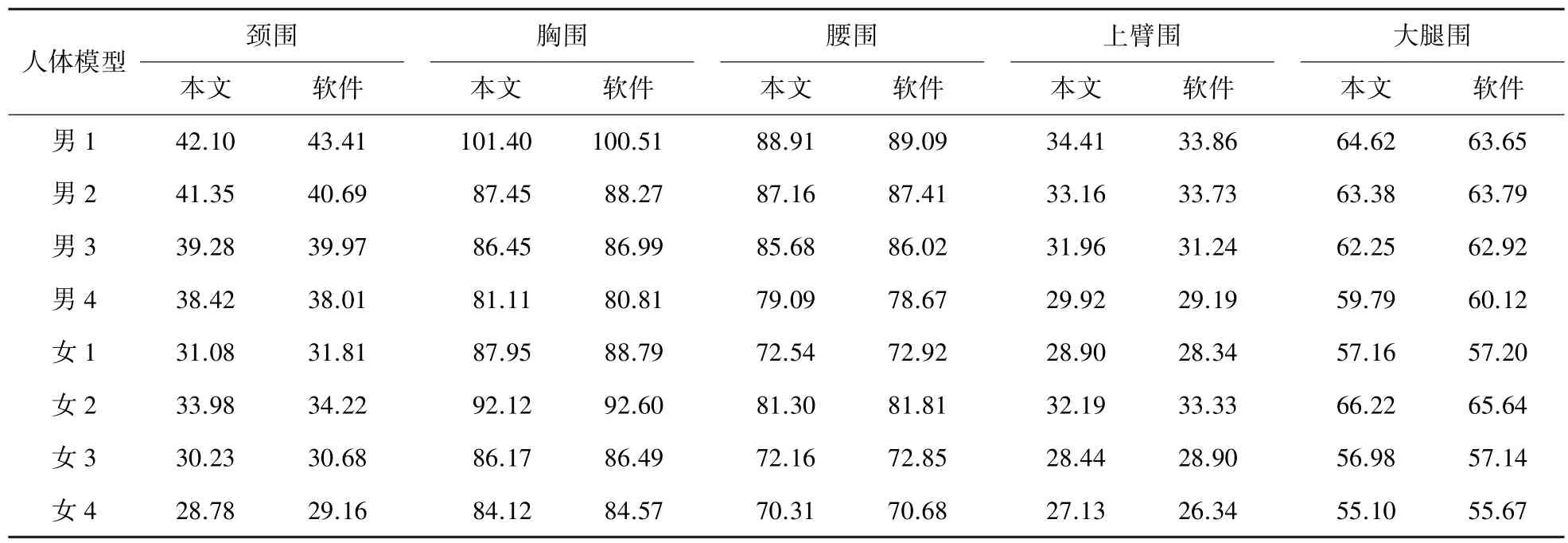
表1 测量结果Tab.1 Measurement results cm
测量误差结果见表2。从测量误差结果可知胸围、腰围和大腿围平均误差较小,而颈围和上臂围由于受分割的影响,导致误差相对较大,但仍在可接受范围内。
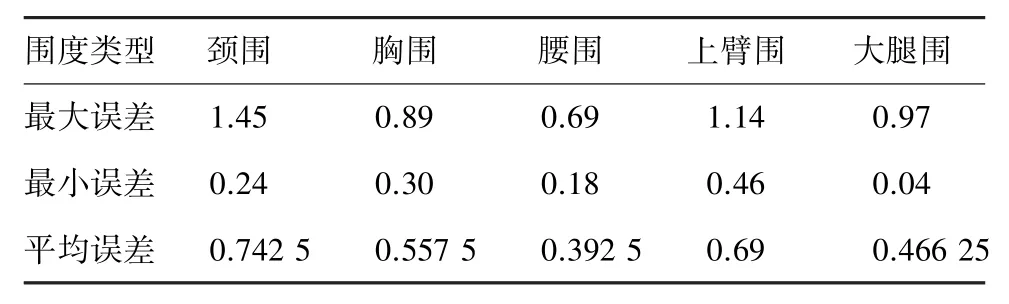
表2 测量误差结果Tab.2 Measurement error results cm
4 结束语
本文采用网格模型顶点的相互可见性和基于偏移表面的形状直径函数进行三维模型分割,能够提高三维模型的分割效果和速度,增加分割的鲁棒性,对不同类别的三维网格模型都能得到较好的分割结果。利用公开的分割评价指标和多种分割方法进行对比评估分析,也证明了本文分割方法的有效性,但是部分模型也会出现分割不准确的情况,比如人体模型上下臂分割不开的问题;对于更加复杂的模型和人体体型变化比较大的模型,分割效果也有待进一步加强。通过对本文测量结果与软件交互式测量结果进行对比,表明基于本文分割得到的测量结果具有一定的可靠性,但是在测量结果的精确程度上有待进一步增强。
