基于改进UCT 算法的国际跳棋博弈系统研究
2022-03-01张家铭王静文李媛
张家铭,王静文,李媛
(沈阳工业大学 理学院,沈阳 110870)
0 引言
随着计算机博弈项目的发展,随之而来的研究也变得越来越多元化,计算机战胜人类成为一个热门的话题。国际跳棋在计算机博弈方面是比较受欢迎的一个棋种。目前国际跳棋64 格已经被解决,每一种局面都算出了最优解。而国际跳棋100 格却有着更加复杂的情况,本文通过对国际跳棋100 格的研究,得出对棋盘的一种评估函数,并对UCT 算法进行改进与测试,并且通过对UCT 算法改进前后对比,得出改进UCT 算法对局面的判断更为准确的结论。
1 国际跳棋简介
1.1 国际跳棋棋盘
国际跳棋是一种古老的游戏,棋盘为10×10 黑白格相间的棋盘,在整个对弈的过程中,白色格子自始至终都是用不到的,棋盘放在对弈双方的中间,每个玩家的右下角应是白色格子,如图1 所示。黑棋先手,然后双方轮流走动己方棋子。

图1 国际跳棋棋盘Fig.1 The board of Draughts
棋子自始至终都是沿着对角线移动和跳吃,对弈的目标是将对方所有棋子吃掉或者形成一个局面迫使对方棋子无法移动。
1.2 国际跳棋下法规则
棋子可以进行跳吃下法,只要对角线方向邻近的黑格内有对方的棋子,并且再过去的黑格是空位,就可以跳过对方的棋子并将对方棋子吃掉;如果没有跳吃的下法,那就只能沿对角线方向前移一格;任何一个棋子到达了对方底线便立刻加冕,从此以后便加冕成“王”;跳吃可以由多次跳吃组成,如果具备连续跳吃的条件,则必须连续跳吃,除非不再具备跳吃的条件,才可以结束跳吃。未加冕的棋子只能向前移动,而在跳吃时可以向前、向后或前后组合。需要注意的是,只有停在对方底线的棋子才可以加冕成王,如果有一个棋子在跳吃过程中途经底线,但是最后没有落在底线,则该棋子无法加冕成王;王棋可以在对角线方向上移动任意多个空格,同样在跳吃的时候,王棋可以跳过对方棋子前后任意数量的空格。所以王棋比一般棋子要珍贵而强大,然而未加冕棋子是可以吃掉王棋的;跳吃的时候,在具有多种选择的情况下,必须选择吃子最多的下法。如果不止一个棋子或者不止一个路线可以跳吃对方同样最多的棋子,就可以自主选择哪个棋子或者向哪个方向行进。
2 国际跳棋博弈系统
计算机博弈游戏直接决定棋力的关键因素为搜索算法与局面评估函数,现在比较传统的算法包括Min-Max 搜索、负极大极小搜索、Alpha-Beta 搜索等等。此类搜索算法均有一个关键是搜索的深度是固定的,当搜索深度达到时,再依次计算估值进行回传,由于不同分支的搜索深度相同,计算量呈指数增加,极大的影响了搜索的速度。
目前比较新颖的算法为UCT 算法,其特点是实现了对不同结点进行深度不同的搜索,并且搜索次数与搜索时间是可控的,若进行足够的模拟一般都可获得较为准确的结果。
2.1 国际跳棋的局面评估
在Min-Max 算法以及Alpha-Beta 等算法中,局面评估函数直接决定了对弈棋力的好坏。显然己方与对方的残留棋子之差与王棋子之差的权值应为最大。
当双方在前期局面对弈时,利用己方与敌方换子等操作来调整双方阵容,进行攻击或者防守;当双方在中局对弈时,往往可移动的棋子数量不多,于是需要适当的可移动棋子来使本方不至于陷入被动;当双方在残局对弈时,有时故意卖子来使对方被动的可能性是存在的,此时搜索深度需要进一步的提高。综上所述,本文的局面评估主要依靠如下几个方面:
(1)己方棋子数量,对方棋子数量;
(2)己方王棋数量,对方王棋数量;
(3)当己方棋子构成一列时,对方棋子不易对该列形成打击,于是己方构成列值数量,对方棋子构成列值数量;
(4)当棋子处于棋盘的中间位置时,更容易对另一方棋子造成致命性打击,并限制对方的棋子移动,本方棋子在中间的棋子数为,对方棋子构成的列数为;
(5)当本方棋子接近对方底线时,该棋子升王的概率会大幅度增加,进而引入平衡因子来评估棋子接近对方底线的程度,己方棋子的平衡因子,对方棋子的平衡因子,对某一局面的价值评估为式(1):

其中,ω(1,…,)为每个因子的权重。
但是需要注意的是真正的局面评估函数往往不是条件越多效果越好的,评估因子的选取往往需要通过具体的局面具体的估值,在国际跳棋还有许多可以利用的估值。
2.2 Alpha-Beta 算法
Alpha-Beta 算法是Min-Max 算法的一种改进,Alpha-Beta 算法增加的为Alpha-Beta 剪枝,即将某些搜索无意义的节点进行剪枝处理,大大的提高了搜索的效率。


Alpha-Beta 算法改进其中之一为迭代加深。迭代加深的是若给每一步都分配一个时间,当某一层搜索结束后,若时间仍然有剩余,则进行下一层的搜索,执行这种操作的好处是可以在给定的时间内进行尽可能深的搜索。
迭代加深的伪码:

2.3 UCT 算法
UCT 算法又名上限置信区间算法,该算法将蒙特卡洛树搜索(Monte-Carlo Tree Search)算法与UCB 公式进行结合,是一种通过对大量节点的模拟,来获得最优解的算法。该算法在搜索过程中,针对不同的分支的搜索深度可以不同,因此,对于某些节点,可以获得更深的搜索深度。
UCT 算法的计算公式(2)为:

其中,v是节点n(非叶子节点)为根节点的所有仿真结果的平均值,反映了该节点n的胜率; T为节点n的访问次数,也是被树内选择策略选中的次数;是一个常数,用来调节深度优先与宽度之间的平衡。
UCT 算法的执行过程如图2 所示,UCT 算法4个具体过程为:

图2 UCT 算法的基本过程Fig.2 UCT Basic Process
(1)选择:从根节点出发,依次对每一个根节点的孩子节点进行选择,选择r最大的节点,并从此节点开始,采用递归的方法选择,直到叶子节点;
(2)扩展:当选择到叶子节点时,将所有合法的下法加到该搜索树中,并初始化值和值;
(3)模拟:对上一步所有合法的下法,依次进行随机下棋,直到终局,如果最后本方胜利,则己方为1,若对方胜利,则己方为0;
(4)反向传播:当叶子节点模拟得出新的和值时,UCT 算法将结果回传,更新搜索路径上的所有节点的和值,其计算公式(3)和公式(4)为:


即父节点的访问次数为所有孩子节点的访问次数之和,将结果从叶子结点开始,依次上传到根节点为止。
需要注意的是如果胜率最高与访问量最高的移动不同时,UCT 算法往往是不稳定的,需要对UCT算法进行改进操作。
2.3.1 UCT 算法的改进
UCT 算法第一个缺点是无论在什么局面下都进行扩展操作,从而导致如果某一局面对本方无利,那么该算法同样会对该局面进行扩展研究;第二个缺点是当UCT 算法进行无限制的扩展后,往后的局面可能会变得更加复杂,容易导致判断失误。为了避免这种情况的发生,故对UCT 算法进行改进操作。
对于某一局面来说,当UCT 算法对某一节点重复选择次后,才对该节点进行扩展,且扩展后的最大深度不超过层。
2.3.2 UCT 算法的不稳定性
通过不断测试的结果中发现,UCT 算法在接近终局时,当本方胜率过高时,UCT 算法的移动就会极具不稳定性,具体表现为会选择一些错误的下法。本文所采取的方法是在接近终局时更换其他稳定性更高的算法。
3 算法比较
3.1 UCT 算法的调整
UCT 算法中的取值不相同,对UCT 算法的强度有很大的影响,这里取节点重复选择次数为20次,最大搜索深度为14 层,搜索时间为15 s,由于UCT 算法的不稳定性,前38 步使用UCT 算法,而后更换为9 层 Alpha-Beta算法,对方是 9 层Alpha-Beta算法,采取的测试平台是CPU:Intel i7-8700,内存:DDr4 2666 MHz 8g,GPU:GTX 1050ti。
测试结果见表1、表2和图3。

图3 UCT 胜率变化Fig.3 UCT Win Rate change Table

表1 UCT-AlphaBeta 对弈结果表Tab.1 Results of UCT-vs-AlphaBeta
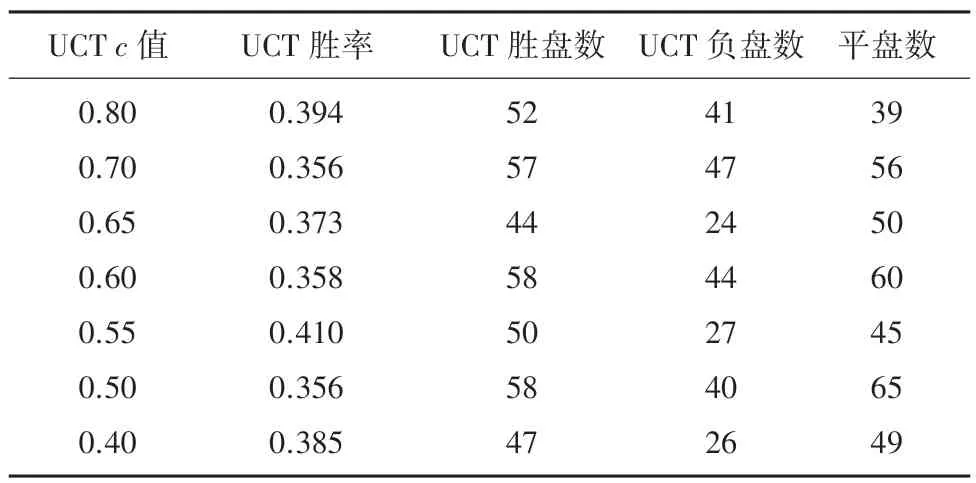
表2 AlphaBeta-UCT 对弈结果表Tab.2 Results of AlphaBeta-vs-UCT
由图3 可以看出,选择了7个不同的值进行对比,UCT 算法先手方值在0.6 处胜率取得极大值,UCT 算法后手方最佳的值仍然在0.6 附近。
3.2 UCT 算法与Alpha-Beta 算法比较
通过原始的15 s UCT 算法与7 s 迭代加深算法进行对比,选取值为0.6,由于UCT 算法的不稳定性,UCT 方前43 步使用UCT 算法,而后使用10 层AlphaBeta 算法,对方采取10 层AlphaBeta 算法,对比结果见表3和表4。

表3 UCT-AlphaBeta 对弈结果表Tab.3 Results of UCT-vs-AlphaBeta

表4 AlphaBeta-UCT 对弈结果表Tab.4 Results of AlphaBeta-vs-UCT
3.3 改进UCT 算法与Alpha-Beta 算法比较
这里改进UCT 算法值选取0.6,对某一节点重复选择次数为35 次,搜索最大深度为12 层。由于UCT 算法的不稳定性,UCT 方前43 步使用UCT 算法,而后改为10 层AlphaBeta 算法,对方采取10 层AlphaBeta 算法。对比结果见表5和表6。

表5 改进UCT-AlphaBeta 对弈结果表Tab.5 Results of Improve UCT-vs-AlphaBeta

表6 AlphaBeta-改进UCT 对弈结果表Tab.6 Results of AlphaBeta-vs-Improve UCT
4 结束语
通过UCT 算法改进前与UCT 算法改进后的对比可以发现,改进后的UCT 算法胜率远远大于原始的UCT 算法,并且在与Alpha-Beta 算法对弈的前中期过程中,往往是改进UCT 方占据优势,从而可以得出采取改进UCT 算法的确可以使博弈水平得到提升。本文所选取的节点重复选择次数和搜索最大深度,也许不是最佳的,可以尝试更改和的值来使得改进后的UCT 算法进一步优化。
