基于滑模变结构控制及预测跟踪的光电吊舱控制方法
2022-02-28马悦飞
马悦飞,林 俤
(1.西安现代控制技术研究所,陕西 西安 710065;2.中国科学院 西安光学精密机械研究所,陕西 西安 710119)
引言
光电吊舱是为光学负载进行稳像和精确跟踪的装置[1-2],为空中侦察和激光通信提供有效平台[3-4]。在光电吊舱稳定回路中,速度环的响应精度直接影响陀螺稳定精度[5-8]。由于非线性摩擦的作用,在低速调转运动中速度环响应存在较大偏差,因此,为减小扰动力矩的影响,需要对摩擦力矩及其他干扰力矩进行补偿[9]。常规PID 控制进行摩擦补偿的前提是精确辨识摩擦模型及相关参数,但获取模型参数较为复杂[10-11]。也有文献提到采用神经网络技术实现模型辨识和摩擦补偿,但运算较复杂,在实际工程应用中实现具有一定难度。另一方面,在视频跟踪回路中,视频跟踪器往往存在几十甚至上百ms 延迟,对跟踪回路带来不利影响[12-13]。
由于滑模控制具有快速响应,对系统参数变化不敏感,无需对扰动模型在线辨识等特点[14],为了降低常规滑模控制产生的抖振现象[15],本文将抗抖振滑模变结构控制预测控制和微分预测跟踪器相结合,提出了改进的基于预测跟踪的抗抖振滑模变结构控制方法,利用DSP28335 控制芯片硬件实现了光电吊舱在线摩擦扰动补偿和预测控制。
1 基本控制原理
在二维转台控制系统中,对于方位、俯仰控制通道中任一通道,一般采用电流环、速度环和位置环3 环控制。由于摩擦、参数摄动及外部扰动的影响,常规PID 控制不能有效地对扰动进行抑制,本文提出了基于抗抖振滑模变结构控制的预测跟踪算法。
设位置指令为 θd,转台实际位置为 θ,令e=θd−θ,则设计滑模切换函数为[16]

式中c>0。则有:

设计滑模控制律为
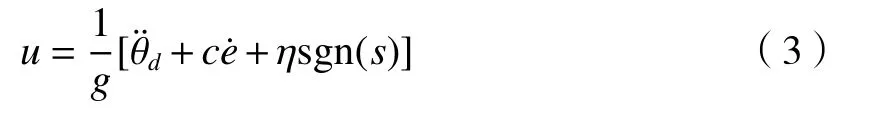
采用Lyapunov 方法判别该控制律的稳定性,定义Lyapunov 函数为

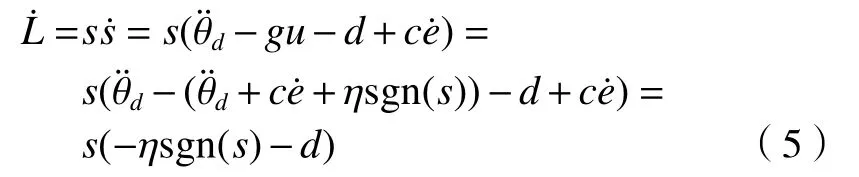

该控制律满足Lyapunov 稳定条件。采用饱和函数sat(s)代替(6)式中的符号函数sgn(s),可在一定程度上消除控制抖振现象。
对视频跟踪器输出的脱靶量信息,与对应时刻码盘值进行运算可得到目标运动的角轨迹信息,但当前计算出的角轨迹是滞后的[17-19]。本文采用非线性微分跟踪器估计出目标运动的角速度,然后进行预测补偿,以消除跟踪器延迟。离散形式的非线性微分跟踪器表达式为
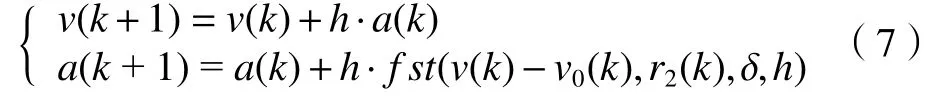
式中:v(k)为第k时刻的速度估计;a(k)为第k时刻的加速度估计;h为采样周期;v0(k)为第k时刻的输入信号;δ决定了跟踪速度。f st(·)为最速控制综合函数,描述如下:

通过(7)式将目标运动角速度和角加速度估计出来,通过(10)式对目标角轨迹进行预测补偿:
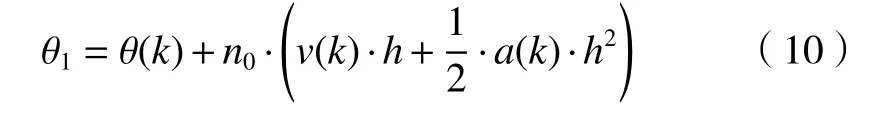
式中:θ1为预测指令角度;n0为预测步长系数。
为了提高精度并进一步抑制滑模变结构控制的抖振现象,通过(7)式估计出目标运动角速率v(k),对(3)式控制策略改进如下:khm0来进行优化,其取值范围为0~1,可表示为
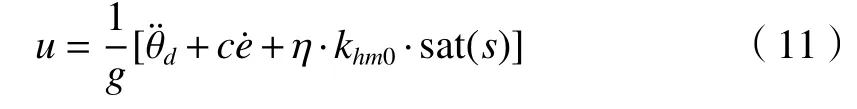
(11)式在饱和函数前增加了自适应比例系数

式中:α1和 β1为常值系数,α1取值范围为0.01~0.9,β1取值范围为1~5。该补偿系数khm0可实现对滑模控制量的自适应调整,减小抖振现象,从而提高光电吊舱跟瞄精度。
图1 给出了自适应比例系数khm0随目标角速度的变化趋势。
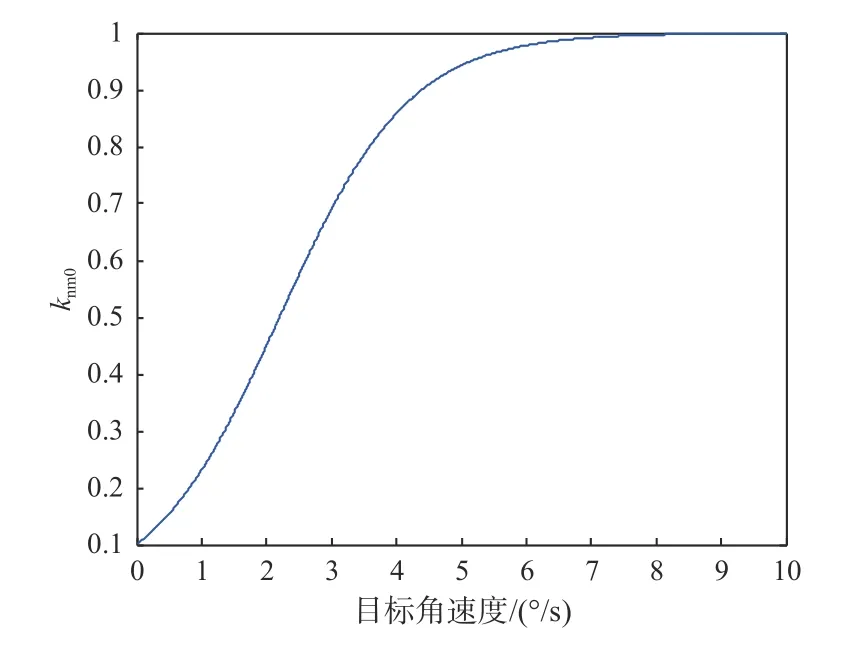
图1 自适应比例系数khm0随目标角速度的变化趋势Fig.1 Tendency of khm0 changed with target angular velocity
2 仿真分析
如图2所示,在封装的Simulink 模型中,控制对象转动惯量J=1.0,滑模自适应相关参数α1=0.1,β1=1,目标运动轨迹设置为幅值为1°,频率为0.3 Hz 的正弦运动,模型中加入视频跟踪器,延迟为30 ms,摩擦及扰动力矩分别采用常规PID 控制和滑模变结构控制进行跟踪精度仿真。
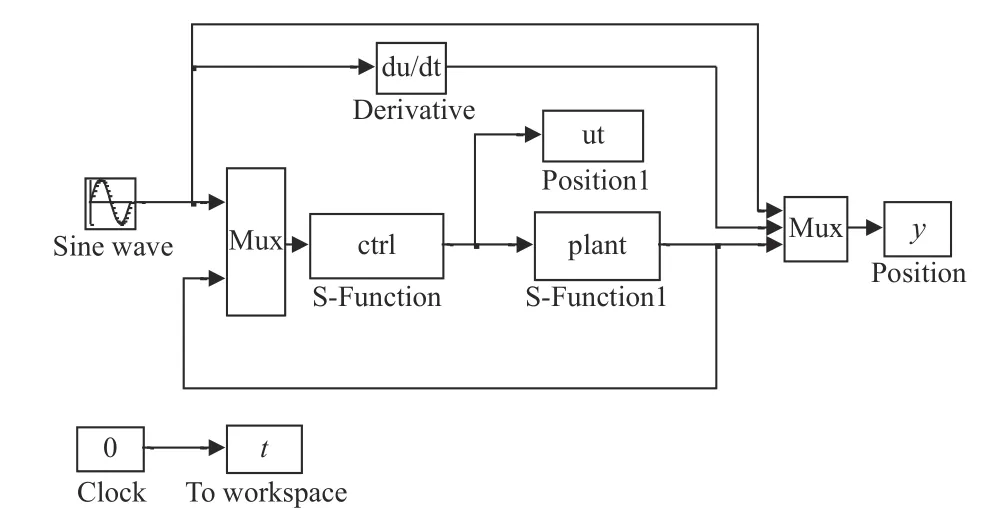
图2 Simulink 模型Fig.2 Simulink model
图3 为常规PID 算法控制仿真图。从图3 可知,位置跟踪存在视频跟踪图像处理及传输延迟,速度跟踪存在摩擦平顶现象,速度跟踪曲线显示在低速附近,由于摩擦力影响,速度响应误差达到了0.3°/s。
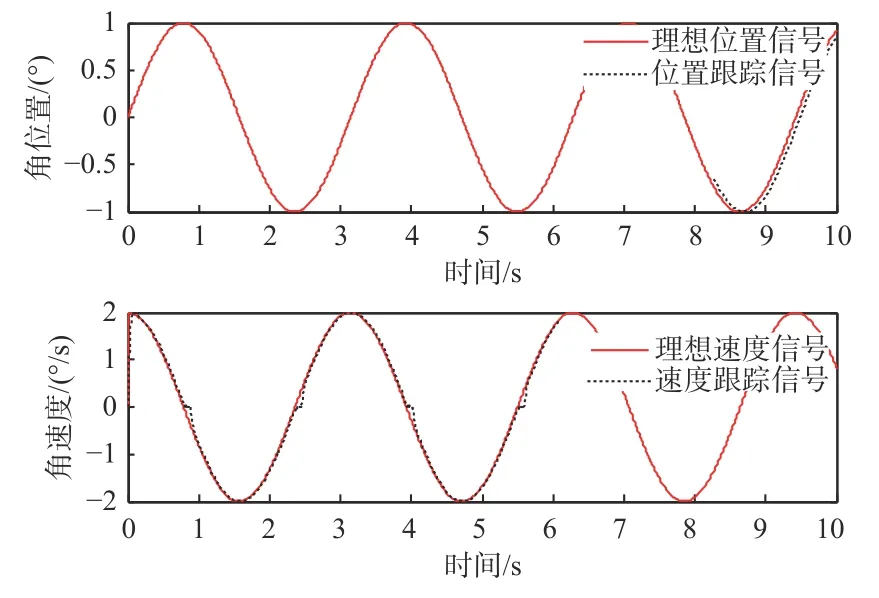
图3 基于常规PID 算法的目标跟踪信号仿真Fig.3 Signal simulation of target tracking based on conventional PID algorithm
抗抖振滑模变结构预测跟踪算法的控制信号仿真结果如图4所示。从图4 可看出,采用预测跟踪补偿了视频跟踪器图像处理的延时,并且滑模变结构控制抑制了摩擦及干扰力矩扰动,提高了速度跟踪精度。
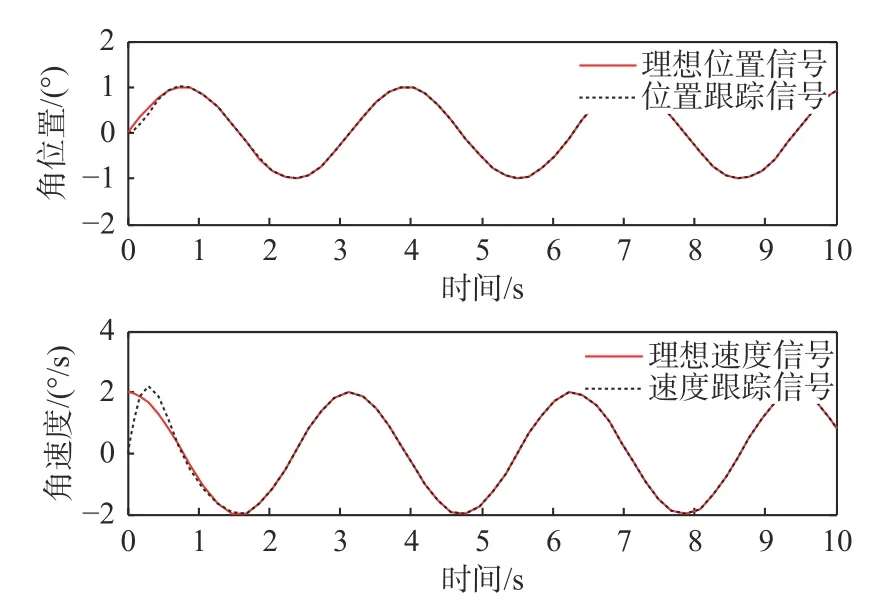
图4 抗抖振滑模变结构预测跟踪算法的控制信号仿真Fig.4 Signal simulation of prediction tracking control of chattering-free sliding mode variable structure
两种算法的跟踪精度对比如图5所示。从图5 可以看出,在模拟仿真条件下,改进算法将位置误差由传统PID 算法的最大值0.12°减小到0.02°,消除了速度跟踪平顶现象,并对视频跟踪器延迟误差进行了有效补偿。

图5 两种算法的跟踪精度对比Fig.5 Comparison of tracking precision of two algorithms
3 实验结果与分析
将上述控制原理在DSP28335 控制板中实现,并采用光电吊舱和模拟动靶标平台进行验证,动靶标实物如图6所示。该动靶标可模拟目标做圆周运动,转靶角速度为45°/s,周期为8 s,模拟出的目标角运动速度为6°/s,视频信号经捕获处理后,可产生类似正弦的吊舱控制信号。采用红外相机跟踪,其实时跟踪效果如图7所示。将脱靶量信息经过422 串口打印到上位机,并保存数据,脱靶量数据如图8所示。

图6 模拟目标运动的动靶标Fig.6 Moving target of simulated target motion

图7 光电吊舱跟踪动靶标效果Fig.7 Tracking effect of photoelectric pod on moving target
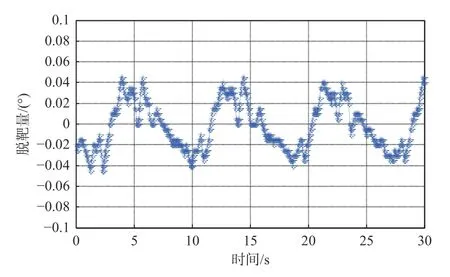
图8 光电吊舱实际跟踪动靶标脱靶量误差Fig.8 Miss distance error of moving target tracked by photoelectric pod
由于动靶标转动并非严格意义上的正弦,存在一定程度的不规则加减速,因此实际预测补偿不完全,精度误差比仿真值稍大,脱靶量误差较仿真误差稍大,最大值为0.045°。在采用常规PID 控制方法的情况下,其误差最大值为0.15°。根据实测数据可知,改进算法将脱靶量误差降低为常规PID 算法的1/3。
4 结论
从以上仿真和实验结果可知,本文提出的基于预测跟踪的改进滑模变结构控制策略,有效抑制了摩擦及不平衡力矩等外部扰动对光电吊舱控制的不利影响,并在一定程度上对视频跟踪器产生的延迟进行了有效补偿。在动靶标做角速度6°/s,0.12 Hz 圆周运动情况下,改进算法脱靶量最大值为0.045°,减小为常规PID 跟踪脱靶量的1/3。但在实际使用过程中,由于目标运动并不规则,所以预测效果受目标机动影响较大,如何建立准确描述目标机动运动的预测模型并加以补偿,成为提高其预测精度的关键。另外,减小视频跟踪器图像处理的延迟,提高实时性,也可以降低预测跟踪的难度。
