用于同步辐射的压电变形镜控制策略数值模拟
2022-02-28王梓齐张军剑冯志华
王梓齐,樊 凯,张军剑,冯志华
(1.中国科学技术大学 精密机械与精密仪器系,安徽 合肥 230026;2.中国科学技术大学 精密科学仪器安徽普通高校重点实验室,安徽 合肥 230026)
引言
同步辐射光因其高亮度、低发射度等优异特性被广泛应用于原子分子物理、化学、生命科学等基础学科研究以及微电子、医药、化工等应用技术研究中,已经成为当今众多前沿科学和高新技术开发中不可替代的最佳光源[1]。为使这一优质光源性能得到充分应用,在束线光学中必须具备与此相适应的聚焦和成像元件,以保证光学传输过程中入射束线发射度不拓展,通量不降级[2]。在过去的20 多年,第3 代同步辐射装置的建设推动了纳米聚焦光学元件的飞速发展,如光栅[3]、复合折射率透镜[4]和菲涅尔波带片[5]等,但是具有能动可调性的光学元件仍处于探索和研究阶段。第4 代同步辐射光源的建设对能够达到衍射极限的光学聚焦元件的需求逐渐凸显,变形镜是同步辐射中对光束线进行聚焦的重要光学器件,其面形精度直接影响着光束线的性能。
变形镜按变形原理不同可细分为压弯变形镜(bendable mirror)和压电变形镜(piezoelectric bimorph mirror,PBM)。压弯镜通过在长镜端部施加力矩,使镜面变形,镜面形貌可以通过设计力矩施加的方式和大小、机械约束形式、镜面形状和厚度分布等方法调控[6-7]。相较而言,压弯变形镜的发展较为成熟,已在3 代光源中大量应用。PBM 技术的研发则相对滞后,目前国际上仅有少数几个同步辐射光源机构开展了相关技术的前期研究。相对压弯变形镜,PBM 对机械加工要求较低,面形控制自由度高,又因压电材料固有的机电耦合属性,其具有更加灵活的控制特性和很大的发展前景[8-9],近年来受到国内外学者的广泛关注。
自1994年第一个单电极PBM[10]提出以来,研究人员不断通过增加电极分区数量来提升控制自由度,获得更加理想的面形结果。2015年,英国Diamond 同步辐射光源Alcock S G 等人[11]在600 mm基底上设计了16 对电极的结构,通过建立压电响应方程,采用逆矩阵方法求解控制电压,成功将PBM 的面形误差RMS 由2 μrad 减小到0.5 μrad。2013年,日本同步辐射装置Spring-8 的Nakamori H 等人[12]研制了一个用于实现衍射极限聚焦的PBM,该PBM 的主要特点之一是电极排列密度高,在100 mm 的基底上设计了18 对分区电极。这种设计大大提高了面形控制自由度和自适应校正精度,使衍射极限聚焦成为可能。经过测试,在Spring-8 光束线BL29-XUL 中通过粗调与精调相结合的在线控制方法调节电压配置,获得了达到衍射极限120 nm 光斑,展现了多电极PBM 的应用价值。2020年,上海应用物理研究所田纳玺等人[13]采用类似设计思路,通过迭代全局优化算法,成功将初始43.4 μm 焦斑尺寸经相位补偿后压缩到12.9 μm,为上海同步辐射光源的快速相位补偿提供了可能。
电极数量的增加可以增加控制自由度,改善因加工或装配造成的镜面空间低频误差,使PBM 面形精细控制成为可能[8-9,14]。但与此同时,这种多电极的设计也面临着控制困难,包括反演后相邻电极间压差超过安全极限的问题[3,15]。由于压电致动单元排列密集,各个致动单元之间的变形贡献高度耦合,面对一个目标面形,如何理清各个致动单元的变形贡献,如何施加合理的控制电压成为亟待解决的工程问题。
1 压电变形镜构成与工作原理
本文的结构参考了Spring-8 的设计思路[16],并通过进一步提升电极数来获得更加精细的面形控制效果,PBM 结构如图1所示。PBM 由单晶硅基底和锆钛酸铅压电陶瓷(PZT-5H)组成。其中,单晶硅基底尺寸为200 mm×50 mm×15 mm,单片PZT 尺寸为200 mm×17.5 mm× 1 mm。在顶部的2 片PZT 上表面分区镀36 个电极,单电极尺寸为17.5 mm×5 mm,相邻两电极分区间隔0.55 mm;底部的2 片PZT 不分区,与顶部对称分布,以减小温度等共模因素对镜面稳定性的影响。
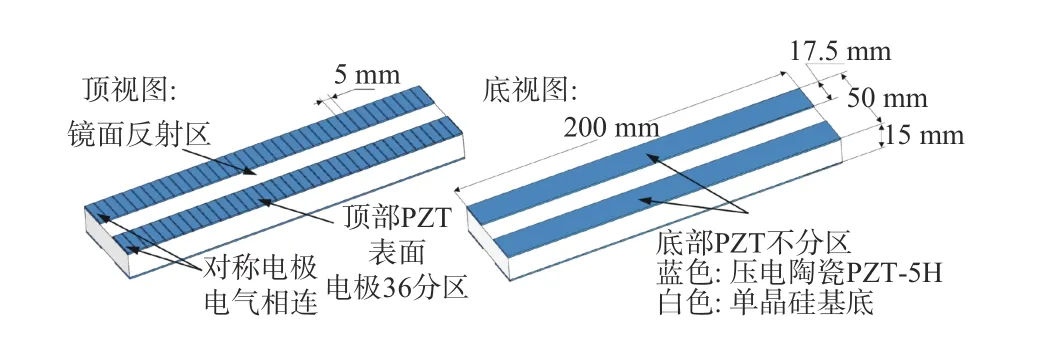
图1 PBM 有限元模型Fig.1 Finite element model of PBM
令PZT 与镜面相接触的电极板接地,当上表面电极通电后,根据逆压电效应,压电材料横向的收缩将带动基底产生形变。一般地,上表面宽度方向对称的2 个电极电气相连,视作一组,输入相同的控制电压。通过精细调节各组电极施加的电压,可以控制PBM 的镜面形貌。同步辐射光经上表面中间的镜面区反射后在测试样品的目标点处汇聚为光斑,如图2所示。

图2 PBM 聚焦示意图Fig.2 Schematic diagram of PBM convergence
2 压电变形镜的数学描述与控制目标
2.1 PBM 数学模型的建立
为了定量描述镜面面形与各极板间施加电压的数学关系,需要构建输入(控制电压)与输出(镜面中心位置各点斜率)的数学模型。一般地,将变形镜的小变形与施加电压的关系视为线性[17-18],具体可分为2 个方面:1)针对单组电极,施加电压大小与镜面中线各点斜率大小呈线性关系;2)多组电极共同施加电压的变形效果等价于单组电极分别施加电压变形效果的线性叠加。据此,构造以下数学关系:
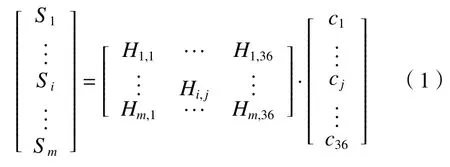
简化为

在有限元仿真软件COMSOL Multiphisics 中各组极板依次施加1 kV 电压,通过采集镜面中线的位移变化,可以绘制36 条压电响应方程(piezo response function,PRF),如图3所示。通过将各条PRF 离散化采样后求采样点处斜率,可以获得变换矩阵H对应列的数据。本文共选择采样点数m=196。
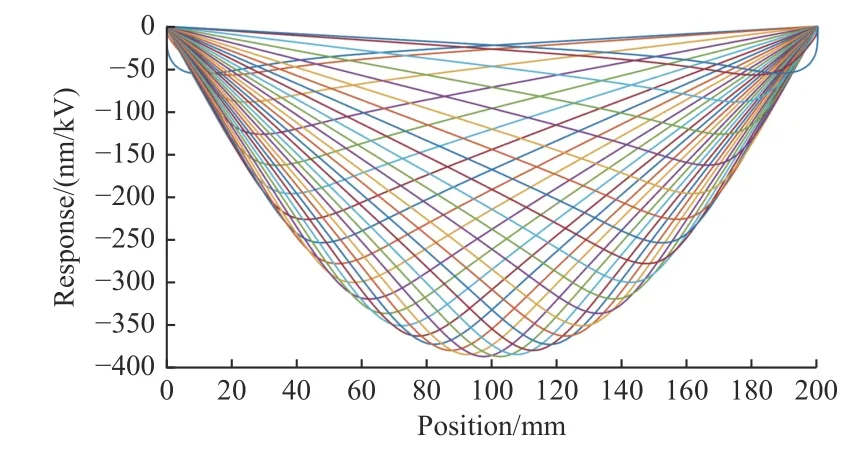
图3 PBM 压电响应方程(PRF)图像Fig.3 Schematic of PBM piezoelectric response equations
2.2 PBM 的反演目标及约束条件
从椭圆一个焦点发射出的所有光线,经椭圆面反射后经相同的光程同时汇聚到椭圆的另一焦点处。得益于该几何特性,在同步辐射中常选取椭圆作为理想面形。Sutter J P [19-20]等人指出,对于如图4所示的椭圆面形,可以通过(3)式实现斜率关系重建。据此,获得了椭圆面形的斜率Sellipse,本文选取的椭圆面形参数如表1所示。
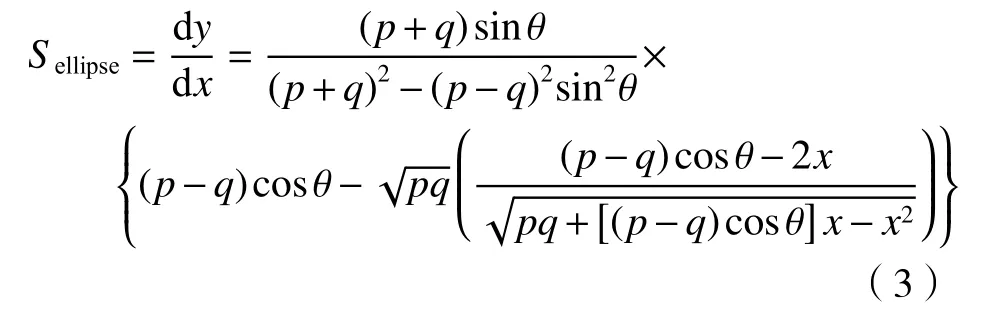
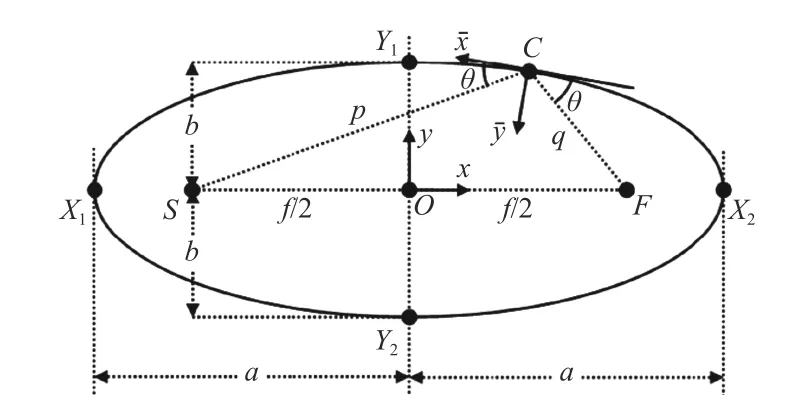
图4 椭圆的坐标重建示意图Fig.4 Schematic of ellipse coordinates reconstruction

表1 椭圆面形参数Table 1 Parameters selection of ellipse surface shape
在工程应用中,镜面面形会受到重力、装配等因素的影响产生畸变[11]。图5所示是仿真镜面受重力后产生的竖直方向位移和斜率变化,将镜面因重力造成的斜率变化记作Sgravity,该畸变需要被PBM 主动变形抵消。由此得到反演目标表达式为
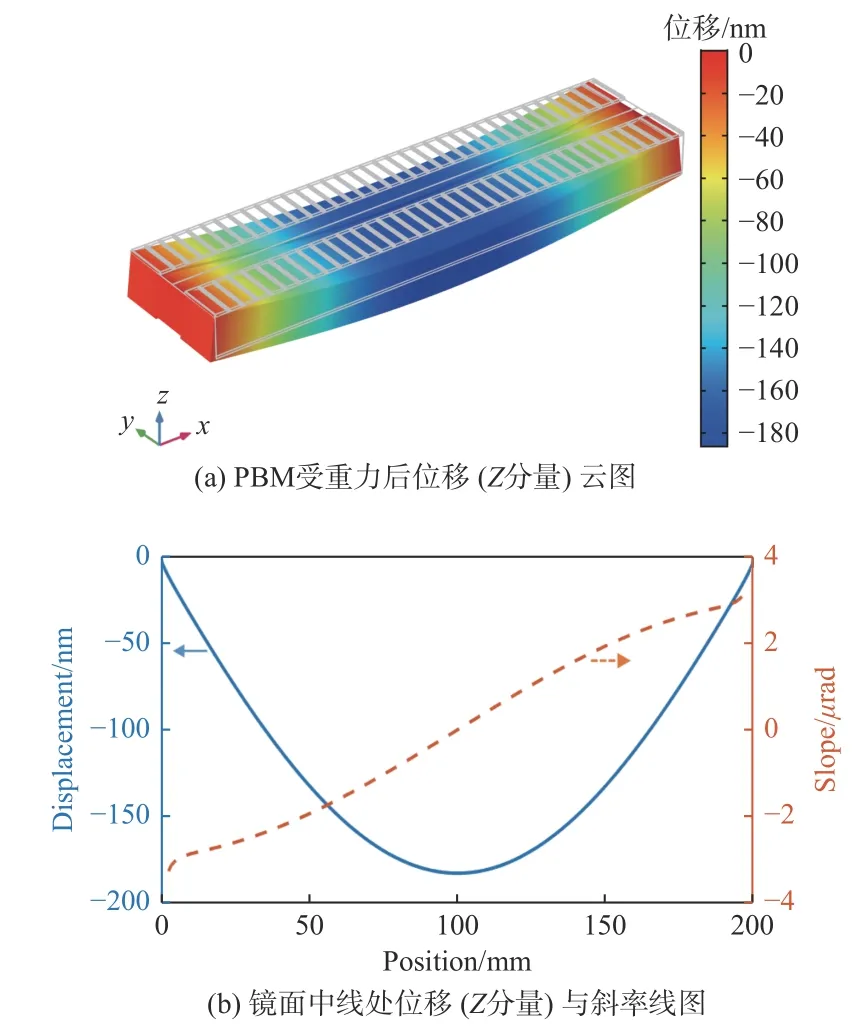
图5 镜面受重力后产生的竖直方向位移和斜率变化Fig.5 Displacement in vertical direction and slope changes of PBM under gravity

此外,控制目标的确定通常还需要传感器对当前面形进行测量,经计算后主动补偿残差。为使模型更加贴近工程实际,向反演目标S0中引入噪声项ζ并记作由MATLAB 中rand()函数随机获得,引入的噪声小于真值的±1%。通过将该反演目标离散化采样,可以获得反演斜率向量采样位置与H矩阵的采样点位置相同,即的尺寸为196×1。
反演后所得的电压施加在电极时需满足一定的约束条件[3,15]。一般认为PZT 施加的电压不应超过2 kV/mm,否则易造成压电陶瓷退极化,甚至击穿介质[21]。另外,相邻分区极板间电压差不应过大,根据电极间距设计的压差不同,一般认为最大压差不得超过500 V/mm,否则会增加极间击穿风险,造成对PBM 的破坏不可逆。本文设计电极间隔0.55 mm,据此确定相邻分区电压差不应超过275 V。
3 电压反演算法及控制效果分析
探讨通过最小二乘法和Tikhonov 正则化两种方法反演出电压配置向量的方法与结果。下面将说明反演时采用最小二乘法的局限性,以及采用Tikhonov 正则化的现实意义和工程价值。
3.1 最小二乘法
最小二乘法(least square method,LSM)是常用的对目标曲线进行参数化拟合的数学方法,具有线性、无偏的特点[22]。该方法以获得拟合量与目标量之间残差的平方和最小为目标,不附加任何约束形式,是一种数学上最优的参数化拟合手段。本文针对反演斜率向量的196 个采样数据拟合电压配置向量中36 个元素,使拟合结果具有最小的残差平方和。LSM 的解析解表达式为
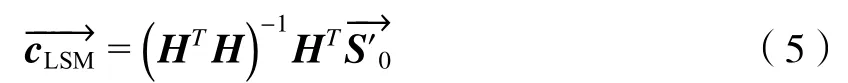
3.2 Tikhonov 正则化
Tikhonov 正则化是对不适定问题(Ill-posed problem)进行回归分析时使用的一种正则化方法[23]。其本质上是一种改良的LSM 估计法,通过放弃LSM的无偏性,以损失部分信息、降低精度为代价,获得的回归系数更符合实际,更可靠。Tikhonov 正则化对病态数据的拟合强于LSM,广泛应用于数据分析、机器学习、统计学习等领域[24]。相关的惩罚项构造泛函,即:
在LSM 的基础上,添加一个与电压波动程度
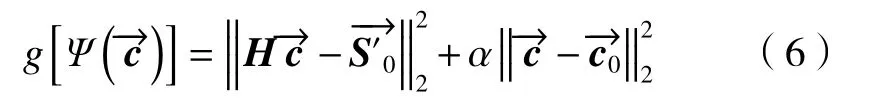
式中:α为正则化参数;为电压先验值。求解电压的过程就是使泛函取得最小值的过程:
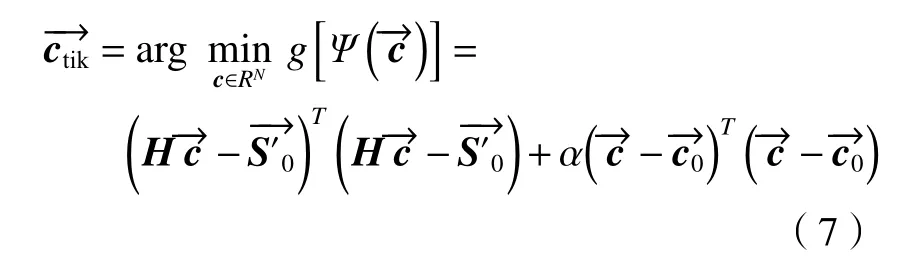
令:

推导得到电压配置向量解析表达式为
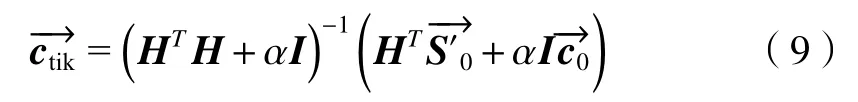
式中I为单位阵。先验值是对目标面形施加电压的粗略估计,往往根据经验估计或仿真得到,包含着对控制结果方向性和范围性的预测。本文选取先验值为0.3 kV。
目前比较有代表性的正则化参数选取策略有:Morozov 偏差原理、广义交叉检验、L 曲线(Lcurve)等准则,其中L 曲线准则应用最为广泛[25]。该方法原理是,在平面上将一系列不同α值时的作为横纵坐标绘制成曲线,曲线呈L 形而得名。
图6所示是本文对应的L 曲线,各个数据点的横纵坐标分别代表面形控制误差和控制电压波动。从图6 可看出,随着α的不断增大,电压波动逐渐减小,但这是以牺牲面形控制精度为代价的。因此,α的选取应综合考量工程实际需求,需在曲线拐点附近选取,最终选取α值为1.25。
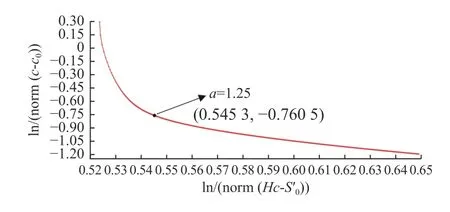
图6 L 曲线绘制与正则化参数的选取Fig.6 L-curve and selection of regularization parameters
3.3 控制结果分析与讨论
分别使用LSM 和Tikhonov 正则化两种方法对控制电压进行求解,电压反演结果如图7所示。经LSM 反演求解,相邻极板间产生的最大压差为1.019 kV,远大于工程中允许的安全压差0.275 kV,极易击穿电极。采用Tikhonov 正则化后,邻近极板最大压差减小为0.174 kV,符合工程实际要求成为可能。
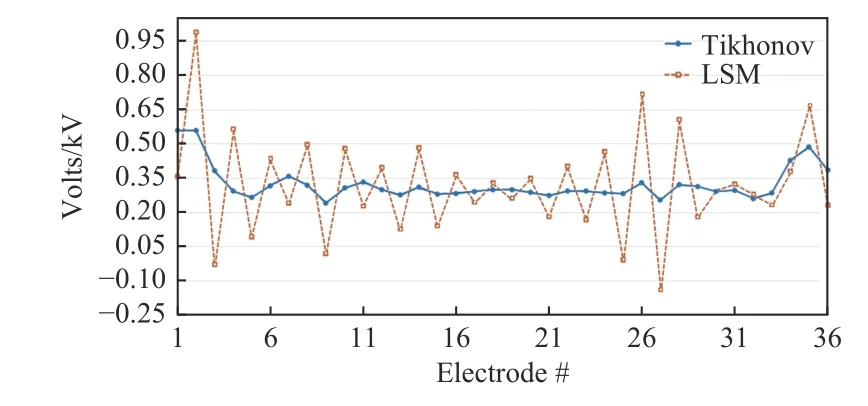
图7 电压反演结果对比Fig.7 Comparison of voltage inversion results
电压大幅波动的原因是,随着压电致动单元排列更加密集,单元间变形贡献耦合程度急剧提升。以变换矩阵H条件数(condition number)衡量耦合程度,经仿真发现,相同约束和尺寸的PBM,随着PZT 分区数量的增加,矩阵H条件数快速增加,如表2所示。数学上称这类条件数较大的矩阵为病态矩阵,这意味着变换矩阵H各列之间相关性增加,对病态矩阵反演问题称为不适定问题。

表2 不同分区数量对变换矩阵H 条件数的影响Table 2 Influence of number of different partitions on condition number of transformation matrix H
因此,当系统引入噪声时,使用LSM 反演的控制结果对带有噪声的离散采样点过拟合,逼近带有噪声的目标面形,表现为相邻电极间大多形成“相互掣肘”的控制电压。采用Tikhonov 正则化通过增加与电压波动情况相关的惩罚项,能够有效避免电压过度波动。从另一个角度来讲,加入了正则化即相当于接受了假设:面形是连续而平缓的,不会高频波动,放弃了电压对噪声部分的过拟合,因此系统对噪声具有鲁棒性。
图8所示为反演目标斜率与采用LSM 和Tikhonov 正则化两种方法所得控制结果残差对比,表3 是两种方法控制结果量化对比。由图8 可知,两种方法均能将面形误差控制在一个较低的水平,但采用LSM 比Tikhonov 正则化斜率残差波动更大,表现出LSM 对于噪声分量的过拟合问题。对表3 数据分析可得,采用Tikhonov 正则化后,面形控制误差相较LSM 降低了21.7%,电压标准差降低了66.7%。Tikhonov 正则化反演结果解决了电压异常波动问题,同时获得了更加出色的面形控制效果,比LSM 具有更加优越的现实应用价值。

图8 反演目标斜率及两种方法控制结果残差对比Fig.8 Inversion target slope and comparison of control residual between LSM and Tikhonov regularization
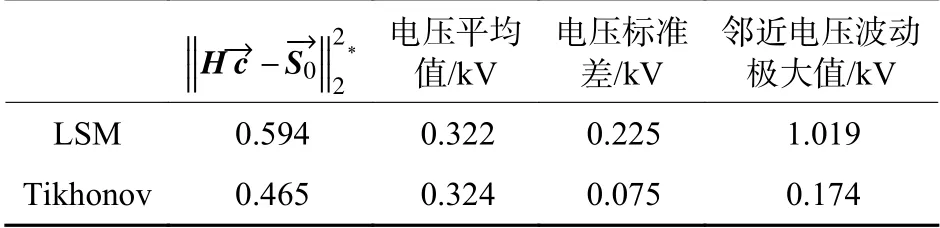
表3 两种方法反演结果比较Table 3 Comparison of inversion results of two methods
4 结论
通过有限元仿真分析,构建了36 组电极分区的PBM 数学模型。为了获得椭圆目标面形,同时结合工程实际,考虑了重力引起的面形畸变和传感器引入的测试噪声,对致动单元控制电压进行反演。研究发现,因致动单元排列密集,各致动单元之间的变形贡献高度耦合,变换矩阵H条件数较大,矩阵呈病态。采用LSM 方法反演后,相邻电极间压差最大可达1.019 kV,远超安全极限,表现出对噪声分量的过拟合问题;采用Tikhonov 正则化反演后,控制电压波动放缓,电压标准差减小了66.7%,面形控制误差降低了21.7%。所得结论为国家同步辐射实验室PBM 闭环控制策略提供了理论指导。
