白鹤滩库区小江碎石土岸坡库水作用稳定性规律分析

2022-02-28李大龙齐洋杨竞易小宇

科学技术与工程 2022年4期

李大龙，齐洋，杨竞，易小宇

(1.浙江华东建设工程有限公司，杭州 310014；2.成都理工大学环境与土木工程学院，成都 610059；3.成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都 610059)

中国西南地区水系发育，河流众多，水能资源丰富，加强水资源综合利用，积极有序推进大型水电基地建设是中国经济社会发展的具体要求。大型水利工程的建设与运营势必会改变原有的地质环境，影响库岸边坡稳定性[1-3]。为进一步了解库水升降作用下堆积体岸坡的稳定性规律，徐文杰等[4]采用三维数值模拟方法对土石混合体边坡库水升降条件下稳定性分析表明，水位上升时岸坡稳定性呈先降低再增高的趋势，水位下降时，边坡稳定性与水位骤降的幅度呈正相关。杨继红等[5]分析了岸坡在非饱和态的瞬态渗流场和瞬态稳定性，指出岸坡滑坡整体稳定性随水位上升而下降，而局部稳定性随着库水位上升表现出先减小后增大的趋势。郭璐[6]采用物理模型试验对水库性滑坡复合渗流动力灾变规律进行了研究，建立了水动力加卸载响应比预测模型。进一步的研究指出，库水升降变幅会加剧对库岸岩土体的侵蚀、携带作用，造成岩土体结构损伤、强度降低[7-11]，从而降低岸坡稳定性。同时，库水位的周期性涨落还会引起岸坡内孔隙水压力变化及渗流场的改变，引发岸坡失稳破坏[12-14]。因此，对水库区岸坡库水作用下的稳定性规律研究显得尤为重要。

白鹤滩水电站是金沙江下游干流四级梯级电站之一，建成后将成为仅此与三峡水电站的第二大电站。白鹤滩水库建成蓄水后，正常蓄水位825 m，死水位765 m，年水位变幅达60 m。小江特大桥右岸斜坡位于白鹤滩水库区小江支库右岸，距大坝坝址约100 km，紧邻格巧高速小江特大桥。该斜坡在自然情况下斜坡上游一侧已发生明显变形。水库蓄水运行后，斜坡将有一半处于库水消落区，届时岸坡岩土体会受到库水长期作用。库水升降作用是否会影响小江特大桥右岸斜坡的稳定性而发生失稳破坏是值得关注的科学问题。鉴于此，在对该岸坡开展详细调查和试验测试的基础上，对其蓄水作用下的渗流场和稳定性进行了分析，为白鹤滩库区库岸斜坡稳定性研究提供有益借鉴。

1 岸坡基本特征

小江特大桥右侧斜坡位于金沙江支流小江右岸，斜坡左右两侧及前缘堆积边界清晰，下游侧以冲沟为界，沟谷深切，排水通畅；冲沟右侧斜坡顺接李开坪子隧道，小江特大桥“主桥墩-隧道进口段”位于该斜坡上。斜坡体正对格巧高速小江特大桥近百米高桥的桥墩，后缘为复建公路S303省道，前缘直抵小江。根据斜坡现今是否有变形，可将此斜坡分为未变形区(Ⅰ区)和变形区(Ⅱ区)，如图1所示。

图1 小江右侧斜坡工程地质平面图

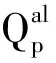
图2 剖面1-1′工程地质剖面图

2 土体物理力学性质

2.1 双环渗透试验

分别在斜坡后缘、中部以及前缘选取3处试验点，采用双环入渗法获取岸坡覆盖层土体的饱和渗透系数。经数据处理，得到沿斜坡从上到下渗透系数分别为k1=8.28×10-2cm/s、k2=1.38×10-2cm/s 及k3=4.86×10-3cm/s，平均渗透系数k=3.38×10-2cm/s，属中-强透水性介质。试验表明，从坡顶到坡脚岸坡渗透性逐渐降低，主要原因是岸坡中后部土体结构松散、密度小(约1.98 g/cm3)；前缘位置堆积层厚度大，形成年代久远，土体结构紧密，有一定的胶结作用，密度较大(2.2～2.4 g/cm3)。

2.2 土体抗剪强度试验

在岸坡消落带附近用中型环刀取原状土样(图3)，进行原状土和饱和土中型直接剪切试验。试样仪器采用浙江华东建设工程有限公司自行设计的中型应力控制式直剪仪(图4)完成。

图3 现场取样

图4 中型应力控制式直剪仪

试验操作按照《水利水电工程粗粒土试验规程》(DL/T 5356—2006)[15]进行，剪切时对4个试样分别施加100、200、300、400 kPa的法向荷载。根据天然状态和饱和状态在不同轴压下所对应的剪应力峰值强度，得到天然和饱和土体的抗剪强度曲线(图5)。计算得到土体天然状态内聚力c为45.74 kPa，内摩擦角φ为39.14°，饱和状态内聚力c为36.44 kPa，内摩擦角φ为31.70°。

τ为剪应力；σ为正应力

3 库水升降作用下岸坡稳定性分析

3.1 数值分析模型和参数

选用1-1′剖面为地质原型，在数值分析模型(图6)中，将卵砾石为设置为一层；角砾、碎石土和块石设置为一层；砂岩、页岩、粉砂岩等视为硬质岩，并归为基岩地层，不考虑因基岩结构面等因素造成的渗流各向异性，将基岩视为不透水边界。土水特征曲线(soil water characteristic curve，SWCC)根据斜坡的饱和渗透系数大小和土的粒径级配曲线，利用Fredlund & Xing模型拟合得到。

图6 斜坡渗流计算模型

稳定性计算方法采用Morgenstern-Price法，同时考虑土体的基质吸力，计算出岸坡在水位变动条件下不同时刻的稳定系数。将SEEP/W模型导入Slope/W模块中，用自动搜索法确定滑面，土条数采用默认值(30条)，Seep/W把各单元格节点水头信息传递给SLOPE/W，从而实现岸坡动态渗流场与稳定性之间的耦合。相关物理力学参数如表1所示。

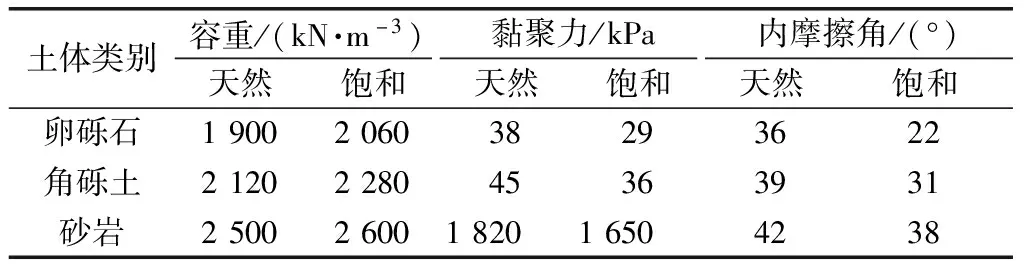
表1 物理力学参数

3.2 库水升降模拟过程

根据白鹤滩水库库水设计调节方案，数值模拟中库水升降过程如图7所示。库水上升阶段，以天然状态稳态分析为初始条件，用瞬态分析方法模拟库水位上升过程中斜坡体的瞬态渗流场(约95 d)，并在水位上升至正常蓄水位825 m后稳定120 d，使坡体得到充分的浸润。库水下降阶段，以库水上升阶段的瞬态分析结果为初始条件，用瞬态分析方法模拟库水位下降过程中斜坡体的瞬态渗流场，用时150 d，水位下降至死水位(765 m)后稳定20 d。稳定性系数按前文方案计算。

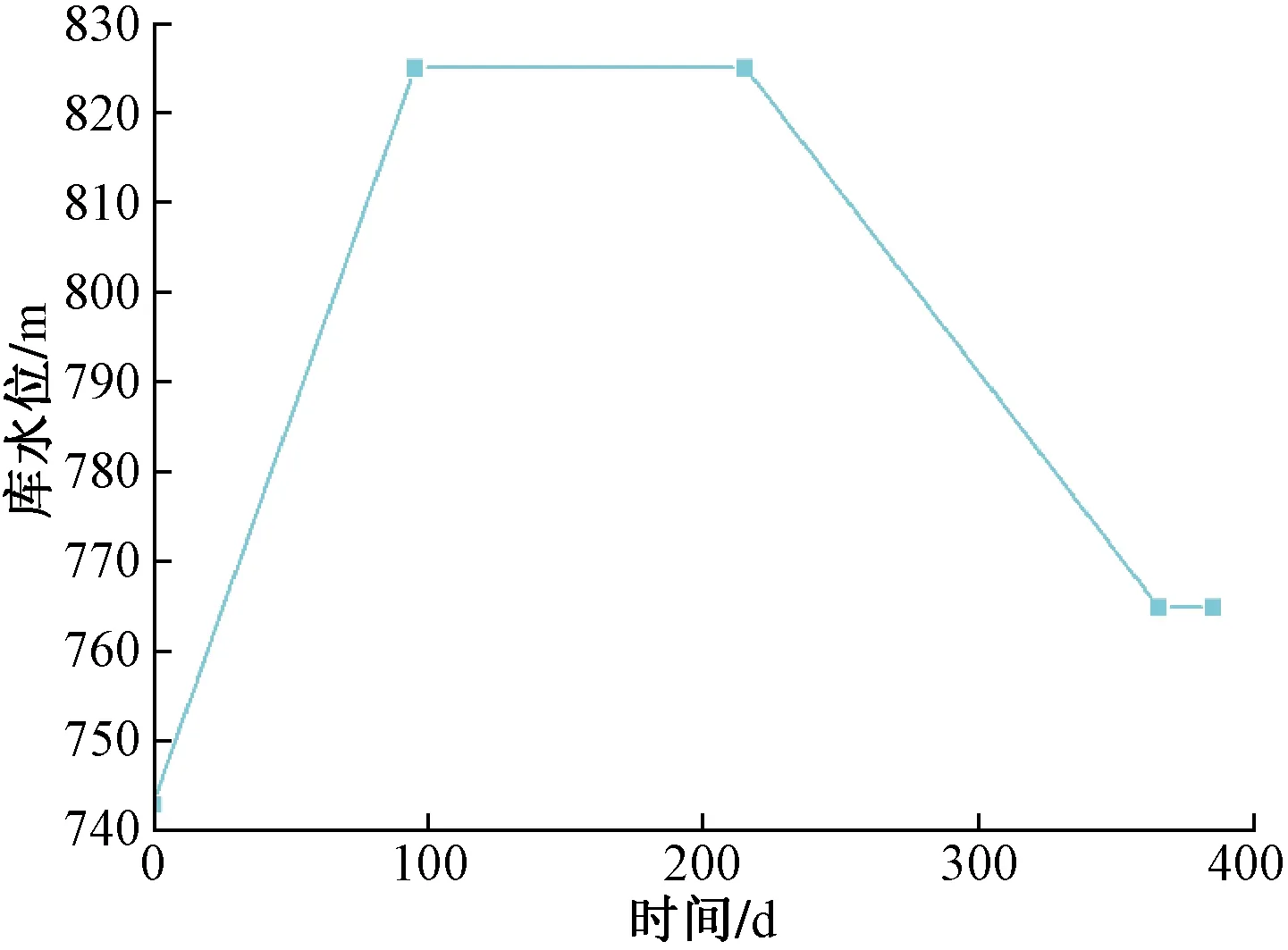
图7 数值模拟库水调节曲线

3.3 库水上升阶段模拟结果分析

图8为库水位上升过程中岸坡内部浸润线变化。库水位上升时，库水由坡面渗入到坡体内部，由于存在渗透差异，岸坡的浸润线上升缓慢，明显滞后于库水位的上升速率，地下水水位略低于库水位，且离坡面越远高差越大，浸润线在坡面处向上弯曲，呈“内凹”状。达到正常蓄水位后，坡面处的浸润线与库水位持平，坡体内部浸润线经过约50 d才达到825 m，滞后性明显。

图8 库水上升过程坡体浸润线的变化

库水位上升过程中，图9为坡体稳定性系数变化。水库蓄水初期(743～775 m)，库水位在775 m附近时，岸坡稳定系数Fs出现最小值(Fs=1.119)；随着库水位不断抬高，地下水位线缓慢抬升，对坡体的浮托力和指向坡内的渗透压力抵消部分下滑力，稳定性系数有所上升。在100 d时库水达到设计正常蓄水位825 m，由于库水上升有着滞后性，在两天后稳定系数达到最大值1.36；之后水库水位保持在825 m，此时浸润线不断上升，土体逐渐趋于饱和，基质吸力逐渐降为零，土体强度不断降低，边坡稳定性也随之降低至1.253。库水上升过程中，岸坡稳定性系数呈现“降低-增加-稳定”的变化规律，岸坡稳定性相较蓄水前稳定性系数降低14.7%。

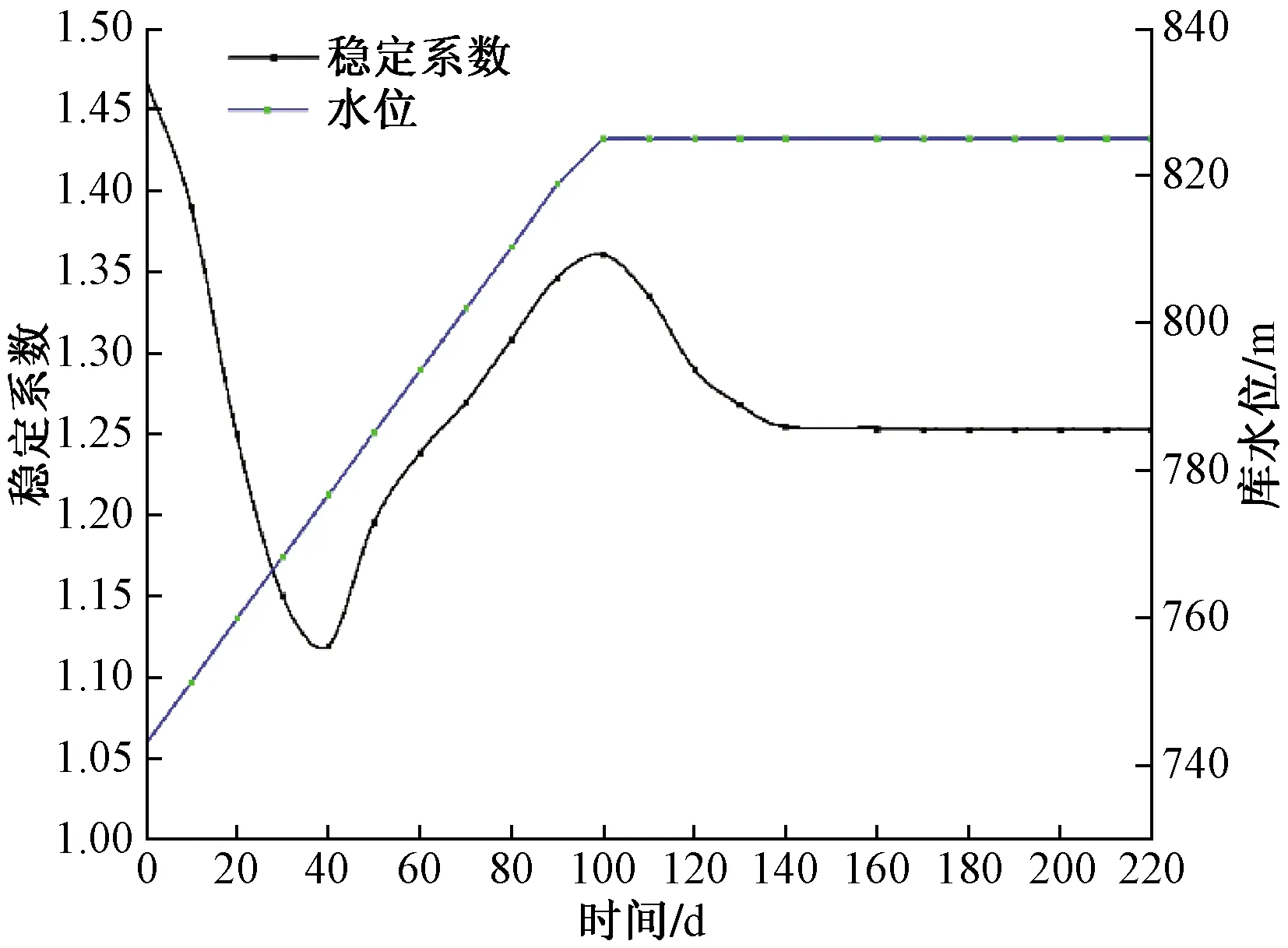
图9 库水位上升过程坡体稳定性系数变化曲线

3.4 库水下降阶段模拟结果分析

图10为库水位下降过程中岸坡内部浸润线变化图。在水库水位迅速降低的过程中，岸坡体内地下水向坡外渗出，补给库水，但由于基质吸力的影响，坡内地下水位明显滞后于库水位下降，导致岸坡内地下水位高，库水位低，浸润线呈“外凸”状。

图10 库水上升过程坡体浸润线的变化

库水位上升过程中，坡体稳定性系数变化如图11 所示。水位在220 d时开始下降，由于岸坡渗流的滞后性，浸润线明显滞后于水位下降，土体内外形成巨大的水头差，导致边坡土体内部的下滑力加大，边坡的稳定性降低；在360 d时，库水位降至死水位附近，此时边坡稳定性系数降低至最小值0.975，发生局部破坏。库水位稳定在死水位后，坡体浸润线仍在缓慢下降，土体含水率不断降低，土体逐渐由饱和态转变为非饱和态，基质吸力逐渐增大，土体抗剪强度也有所增大，边坡稳定性系数也随之增大至1.034。库水上升过程中，岸坡稳定性系数呈现“降低-增加-稳定”的变化规律，岸坡稳定性相较最高水位时下降了17.5%。