基于多层CatBoost的电力系统暂态稳定评估

2022-02-28王强陈浩刘炼

科学技术与工程 2022年4期

王强，陈浩，刘炼

(三峡大学电气与新能源学院，宜昌 443000)

电力系统暂态稳定是指电力系统在受到大扰动后，各发电机保持同步运行并过渡到稳定运行状态的能力[1]。暂态失稳易引发连锁故障进而导致发生大面积停电事故[2]，这不仅造成重大经济损失，而且对人们的生产、生活产生了不可预估的影响。快速、准确的暂态稳定评估(transient stability assessment，TSA)能及时为系统的紧急控制提供参考依据，对维持系统的安全稳定具有重要意义。

目前，TSA方法主要包括时域仿真法[3-4]、直接法[5-6]和人工智能法。时域仿真法，评估精度高，但由于计算速度的限制，难以应用于在线评估；直接法，能快速提供TSA结果，但评估精度不高，难以应用于复杂的大规模系统。人工智能法以机器学习为核心，它从离线数据中寻求系统状态参数到暂态稳定结果间的映射关系，基于该映射关系根据系统在线运行数据实现在线TSA，具有计算速度快、评估精度高等优点[7-8]。随着新一代智能电网的建设，广域测量系统(wide area measurement system，WAMS)/同步相量测量单元(phasor measurement units，PMU)迅速普及[9]，为历史数据的储存和在线数据的采集提供了便利，基于机器学习的在线TSA成为了研究热点[10]。

文献[4]使用差分进化算法改进极限学习机，提高了TSA模型的准确率和鲁棒性。文献[8]首先使用改进的卷积神经网络(convolutional neural networks，CNN)和双向长短时记忆网络进行特征提取，然后使用LightGBM算法预测系统暂态稳定状况。文献[11]采用XGBoost算法进行TSA，并利用注意力系数改进XGBoost算法的损失函数，提高了XGBoost算法的召回率。文献[12]利用焦点损失函数改进LightGBM算法，提升了在不平衡样本上的评估精度。文献[13]采用多个结构相同、参数不同的CNN进行TSA，评估结果综合多个CNN模型的分析，并对评估结果为不确定的样本采取时域仿真进一步分析。

随着现代电力系统迅速发展，在该领域的研究中仍面临着以下问题：①现代电力系统的规模更大，需获取的状态参数特征迅速增加，分类器易陷入“维数灾难”[14]，另外过多的冗余特征、无关特征，将损害TSA模型的泛化能力；②随着大规模新能源并网以及新装置的不断应用，电力系统的运行环境更加复杂、不确定性因素更多，这对TSA模型的精确性和泛化能力提出了更高要求；③由于设备故障、测量数据的远距离传输导致出现数据错误，常规TSA模型的鲁棒性可能无法满足要求。

针对以上问题，提出一种结合最大相关最小冗余(maximal relevance and minimal redundancy，mRMR)[15-16]集成方案和多个CatBoost(unbiased boosting with categorical features)[17-18]分类器的TSA方法。首先，运行多个mRMR特征选择过程，充分挖掘输入特征与暂态稳定结果间的隐含关系，筛选出多个不同关键特征集；然后，训练多个CatBoost模型，并综合多个CatBoost模型的分析。最后，在IEEE 39节点系统和某省级电力系统上进行了性能测试实验，并验证了所提TSA方法的有效性。

1 输入特征及暂态稳定结果标签

应用机器学习算法来建立系统状态参数到暂态稳定结果间的映射关系，首要任务是确定输入特征和构建暂态稳定结果标签。

1.1 输入特征的选择

在基于机器学习的TSA建模中，输入特征分为两类[11]：第一类输入特征由故障前和故障后的电气量特征构成；第二类输入特征由故障前的电气量特征构成。故障前的特征可在电力系统稳态运行时监测到，而故障后的特征只有在故障发生后才能监测到，系统的暂态过程极为短暂，这给电网操作人员的反应时间极短。而根据系统的稳态运行信息，预测系统的暂态稳定性，电网操作人员能够拥有更加充足的时间分析当前系统的运行状况，并能及时为后续控制措施的制定提供依据，所以采用第二类输入特征进行建模。

如表1所示，列出了能够反映电力系统的暂态稳定状况的部分稳态运行电气量信息。并且选择使用这些电气量信息来构建输入特征集D。

表1 电气量特征

1.2 暂态稳定判定规则

对于故障前的TSA，使用电力系统的暂态稳定裕度(transient stability margin, TSM)来量化从当前工作点到稳定边界的距离，常用的TSM表示方法有扩展等面积准则法、能量函数法、极限切除时间法等。在极限切除时间法中，故障后的极限切除时间(critical clearing time，CCT)能够反映电力系统的暂态稳定性，CCT越长则系统保持暂态稳定的能力越强，如果实际切除时间(actual clearing time，ACT)小于CCT，可认为系统能够稳定运行，否则认为系统不稳定。因此，将事故i下的TSM定义为

(1)

式(1)中：CCTi为电力系统某个位置在事故i下的CCT；ACTi为故障点在事故i下的ACT；TSMi取值为(-1 1)，因此，暂态稳定结果标签可构建为

(2)

2 多组关键特征集的构造

2.1 mRMR算法简介

2.1.1 mRMR准则

互信息常用于评价两个随机变量间的相关性，互信息值越高则表示这两个随机变量的相关性越大。若对于两个离散的随机变量X与Y，其联合概率密度函数为P(x,y)，边缘密度函数为P(x)、P(y)，则互信息MI(X，Y)可定义为

(3)

基于互信息原理，关键特征集S与暂态稳定结果间的最大相关性、关键特征集S中所有特征的最小冗余性可分别定义为

(4)

(5)

式中：|S|表示关键特征数目；MI(Fi,y)为特征Fi与暂态稳定结果y间的互信息值；MI(Fi,Fj)为特征Fi与特征Fj间的互信息值。

mRMR的目标是最大化特征与暂态稳定结果间的相关性、最小化不同特征间的冗余性。通过对相关性和冗余性的权衡，并将式(4)与式(5)组合建立关键特征集S的mRMR准则为

maxΦ(U,R),

Φ=U-R

(6)

2.1.2 增量搜索算法

在应用中，mRMR采用增量搜索算法[16]选取式(6)中Φ(·)所定义的最优近似特征。因而，采用增量搜索算法进行特征选择的具体流程如下。

步骤1定义关键特征集合S；

步骤2根据式(3)计算每个特征Fi与暂态稳定结果间的相关性，并按相关性大小排序，选择与暂态稳定结果最相关的n(n≥1)个特征作为第一选择特征，将其添加到集合S中。

步骤3在已选特征的基础上，对于剩余特征，根据式(6)中的mRMR标准选择下一个特征Fj，可表示为

(7)

步骤4将步骤3选择的特征Fj添加到集合S中，重复步骤3直到得到所需特征数目的关键特征集S。

2.2 基于mRMR集成方案的关键特征筛选

采用一种mRMR集成方案，其示意图如图1所示，在该过程中，并行生成m个不同的mRMR特征选择过程。每个特征选择过程首先选取不同的第一选择特征。随后，运行m个不同的增量搜索算法，筛选出m组不同的关键特征集。不同关键特征集间相互补充，增强TSA模型的鲁棒性。

图1 mRMR集成方案示意图

3 基于多层CatBoost的TSA模型

3.1 CatBoost算法简介

CatBoost算法是梯度提升决策树(gradient boosting decision tree，GBDT)框架下的新型改进算法。它将对称决策树作为基学习器，对称决策树的对称结构使其参数更少、训练和测试速度更快。并且，在算法训练中采用排序提升方法来避免标准GBDT模型所存在的梯度偏差问题，进而提升了算法的准确性和泛化能力，保证了TSA的可靠性。

3.1.1 CatBoost的整体迭代过程

在模型训练中，每轮迭代生成一个弱学习器，并让本轮迭代的损失函数最小。假设损失函数为L[y,f(x)]，每轮迭代的目标函数ht可定义为

(8)

式(8)中：ht是从一系列H函数中选择的树；E为期望函数；Ft-1(x)为上一轮迭代中所获得的强学习器。

(9)

随后，得到本轮迭代的强学习器为

F(x)t=F(x)t-1+αht

(10)

式(10)中：α为学习率，即模型更新的步长。

3.1.2 排序提升

在迭代过程中，GBDT算法使用相同的训练样本计算在每轮迭代的梯度，并将式(9)表示为

(11)

式(11)中：n为训练样本数目；{xk,yk}为第k个训练样本，k=1, 2,…,n，其中yk∈{0,1}。

因此，这导致根据训练样本计算得到的梯度分布gt(xk,yk)|xk与数据空间中梯度的真实分布gt(x,y)|x相比存在偏差[17-18]。根据式(11)求得的目标函数ht就与式(8)中ht的定义产生了偏差，进而影响最终模型F(x)的准确性和泛化能力。

CatBoost算法则采用了排序提升方法来进行梯度的无偏计算，其基本原理为：对于每一个样本xi，都使用不包含样本xi的训练集单独训练一个模型Mi，并使用模型Mi来计算样本xi上的梯度。同时，文献[17-18]证明了排序提升方法的有效性。

3.2 提出TSA综合模型

为最大限度地提升TSA模型的精确性，采用多个不同的关键特征集分别单独训练多个CatBoost分类器，然后将它们集成到暂态稳定分析中，并提出TSA综合评估模型，其示意图如图2所示。

图2 TSA综合模型示意图

构建TSA综合模型的具体流程为：通过采用mRMR集成方案，从输入特征集中选取m组不同的关键特征集。以这m组关键特征集和相应的暂态稳定结果标签作为输入，分别对m个CatBoost算法进行训练和测试，并将训练好的CatBoost模型结合构建TSA综合模型。每个CatBoost模型的输出分别为：y1、y2、…、ym，根据多数投票表决方式得到最终输出结果。

4 TSA的具体流程

基于多层CatBoost分类器的TSA流程图(图3)，包括离线训练、在线应用及模型更新。

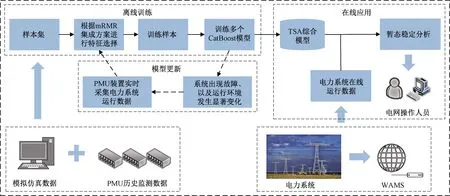
图3 TSA流程图

4.1 离线训练

离线训练步骤如下。

步骤1根据电网公司所储存的PMU历史监测数据和预想事故集的模拟仿真获取样本集。其中，PMU历史监测数据包含了电力系统实际存在的运行状态和大扰动事故下的安全信息；基于预想事故集的模拟仿真，针对每个故障，应考虑系统的网络拓扑变化、负荷波动以及发电机出力变化等因素的影响，尽可能覆盖更多的电力系统潜在运行行为。

步骤2采用mRMR集成方案进行特征选择。在该步骤中，生成多个不同的mRMR特征选择过程，筛选出多组不同的关键特征集。

步骤3将多组关键特征集和相应的暂态稳定结果标签作为训练样本，训练多个CatBoost模型，并结合不同的CatBoost训练模型构建TSA综合模型。

4.2 在线应用

根据WAMS提供的电力系统在线运行数据，结合mRMR特征选择结果选取出相应的电气量特征输入训练好的CatBoost模型，然后对多个CatBoost模型的分析结果进行综合，得到最终的评估结果。若判定为不稳定则提示电网操作人员对系统运行状况进一步分析，考虑是否采取必要的控制措施，避免出现连锁故障和发生大面积停电事故。

4.3 模型更新

电网在实际运行中受到多种因素的影响。如电网紧急事故、经济调度以及检修计划等会导致电力网络拓扑结构的变化；对于负荷需求，天气和季节是一个重要影响因素；同时随着大规模新能源并网以及分布式发电技术的发展，根据实际电网的需求会造成发电机/负载功率分布的变化。因此，仅靠离线训练无法覆盖电网所有可能存在的运行行为，为不断完善TSA综合模型的内容，进行更新步骤是必要的。

考虑上述影响因素，在系统出现故障、以及运行状态发生显著变化时，通过PMU装置对电力系统运行数据实时采集，并选择关键特征对CatBoost模型再训练。

5 算例分析

分别在IEEE 39节点系统和某省级电力系统上进行性能测试实验，以验证所提出的TSA综合模型的有效性。所有测试在一台装有Intel Core i5 处理器和8 GB内存的计算机上进行。mRMR集成算法使用R语言mRMRe包搭建。CatBoost算法在Jupyter环境下基于Python开源机器学习库catboost 0.24.2构建设置基学习器数目为300，最大深度为5，学习率为0.05。

5.1 IEEE 39节点系统

IEEE 39节点系统的拓扑图如图4所示，该系统由39条母线、10台发电机(G1～G10)和46条输电线路组成。

图4 IEEE 39节点系统拓扑图

5.1.1 样本集的生成

使用PSS/E软件进行仿真，并调用Python程序控制PSS/E软件进行仿真数据的自动收集。发电机设置为GENROU模型，负载采用恒阻抗模型，使负载在70%～130%范围随机波动，并相应调整发电机出力大小来模拟出不同的运行方式。记录每种运行方式下的稳态运行参数信息，针对不同运行方式，在节点、线路的不同位置设置三相短路接地故障，并计算不同故障的CCT。由于实际中存在样本不平衡情况，在随机剔除部分不稳定样本后，收集到4 152个样本(包括：3 062个稳定样本，1 090个不稳定样本)，每个样本包含660个电气量特征和一个相应的暂态稳定结果标签。

为保证测试结果的客观性，将80%的样本用于训练，20%的样本用于测试，采用5倍交叉验证法重复实验，取5次测试结果的平均值。

5.1.2 模型性能评价指标

针对不稳定样本漏判和稳定样本误判的代价差别，使用准确率Acc和召回率Rec指标来衡量训练模型的好坏。准确率和召回率的定义为

(12)

(13)

式中：TP为不稳定样本被正确分类的数量；TN为稳定样本被正确分类的数量；FP为稳定样本被错误分类的数量；FN为不稳定样本被错误分类的数量。

根据定义可知，准确率为所有样本中被正确分类的比例，召回率为不稳定样本中被正确分类的比例。

5.1.3 基于mRMR集成方案的特征选取

mRMR算法选择的关键特征数目与CatBoost分类器的准确率、训练时间的变化关系图，如图5所示。可以看出，在选取150个关键特征时准确率达到最大值，之后特征数目的增加准确率不再升高，而且略有下降。另外训练时间与特征数目成正比，在特征数目减少时，训练时间也随之降低。因此，使用mRMR算法来剔除冗余特征、无关特征，降低特征空间维数，有助于提高计算效率和增强模型的泛化能力。

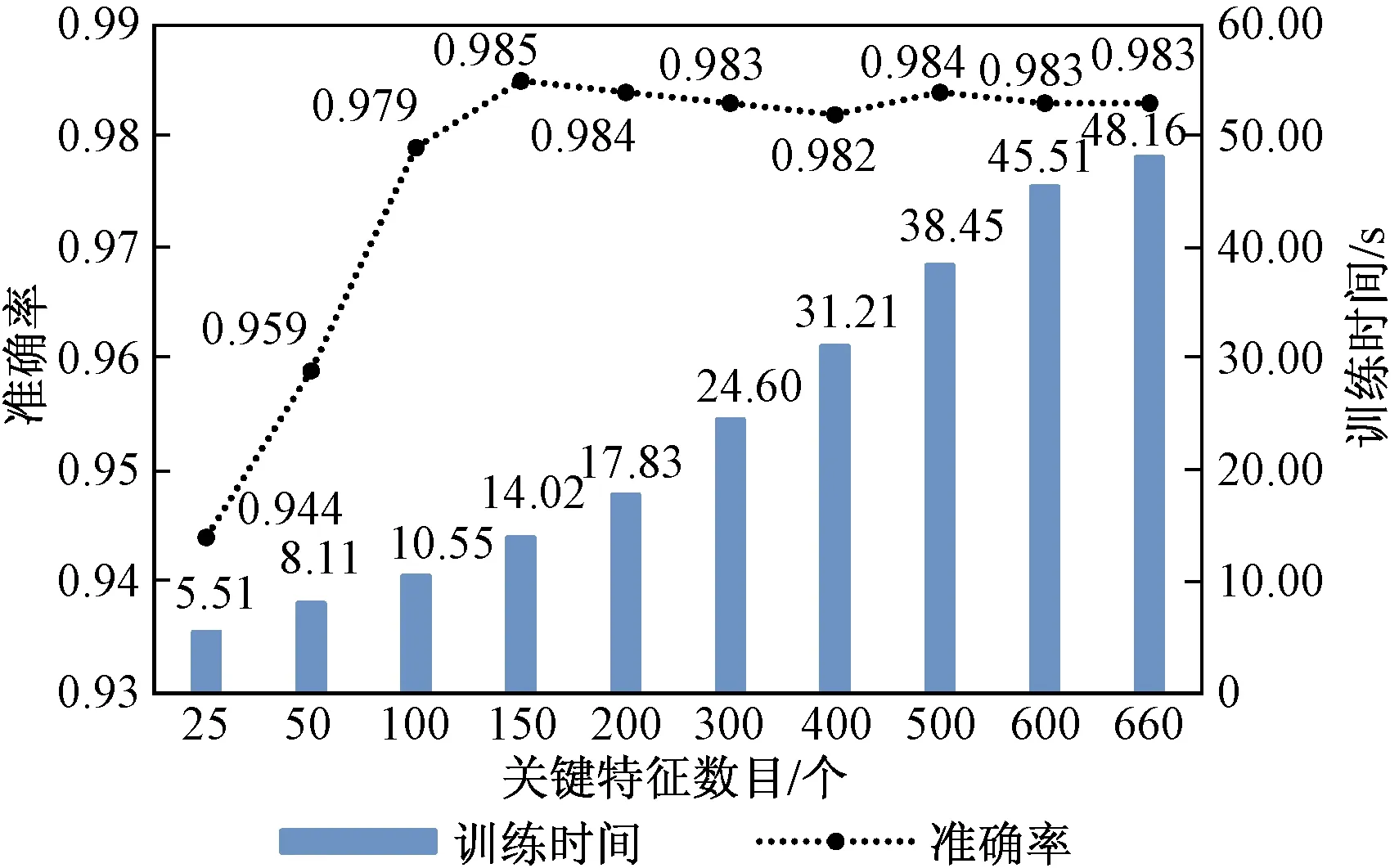
图5 不同关键特征数目的训练时间和准确率

mRMR集成方案设置为5个mRMR特征选择过程(m=5)，每个过程分别选择150个关键特征。如表2所示，给出了mRMR集成方案选择的部分关键特征。

表2 mRMR集成方案特征选择结果

5.1.4 不同模型性能比较

使用仿真所获得的样本对支持向量机(support vector machine, SVM)模型、决策树(decision tree, DT)模型、深度神经网络(deep neural networks, DNN)模型、XGBoost模型、单个CatBoost模型以及TSA综合模型进行TSA评估。其中，SVM模型采用高斯核函数，并通过交叉验证法和网格法寻找最优的惩罚因子C和核参数γ；DT模型设置为默认参数；DNN模型包含5个隐含层，每层神经元数依次为300-200-150-100-50；XGBoost模型采用与CatBoost模型相同的参数。不同模型的测试结果如表3所示。

由表3可知，TSA综合模型的准确率为0.995、召回率为0.997，远高于另外5种评估模型。由于使用多个不同的关键特征集训练多个CatBoost模型，能够充分挖掘输入特征与暂态稳定结果间的映射关系，进而提高了TSA的精确性。另外，对于SVM模型，在小规模系统上通常具有较好表现，但当系统规模过于庞大时，将耗费大量的机器内存和运算时间；对于DT模型，当树的深度很大时，会建立过于复杂的规则，这易导致模型出现过拟合；DNN模型的计算成本过高，且存在黑箱问题，其做出判断的机理难以被解释；XGBoost模型实现了大规模并行梯度提升，但仍然存在梯度偏差问题，在泛化能力上不如CatBoost模型；CatBoost模型有效解决了梯度估计偏差问题，在预测精度上也具有一定的优势。

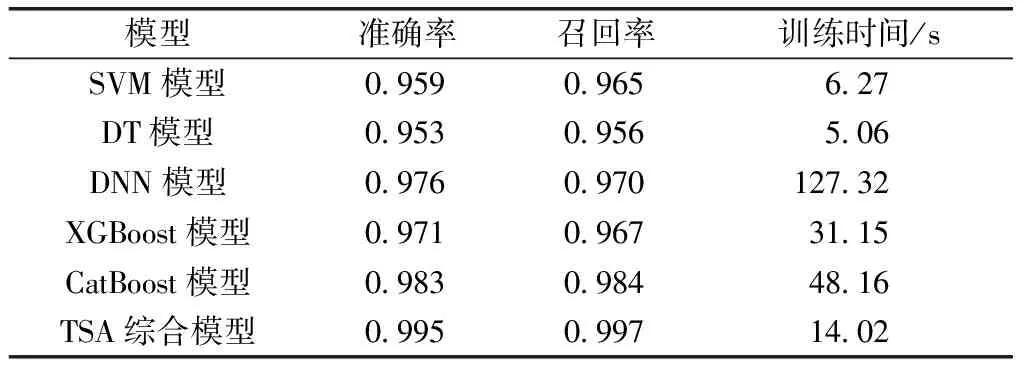
表3 IEEE 39节点系统上的测试结果

5.1.5 泛化能力测试

考虑实际运行中的电力网络拓扑结构变化、发电机/负载功率分布变化以及负载特性变化，并将系统运行状态改变后生成的新样本用于测试，以验证TSA综合模型在新样本中的适应能力。

(1)拓扑结构变化。将原来电力网络的完全拓扑结构改变为相应的N-1、N-2、N-3拓扑结构，如表4所示。相应的测试结果，如图6所示。

图6 不同拓扑结构变化测试

表4 不同拓扑结构变化类型

(2)发电机/负载功率分布变化。不同发电机/负载功率分布变化的测试结果如表5所示，变化范围与原始分布相对应。

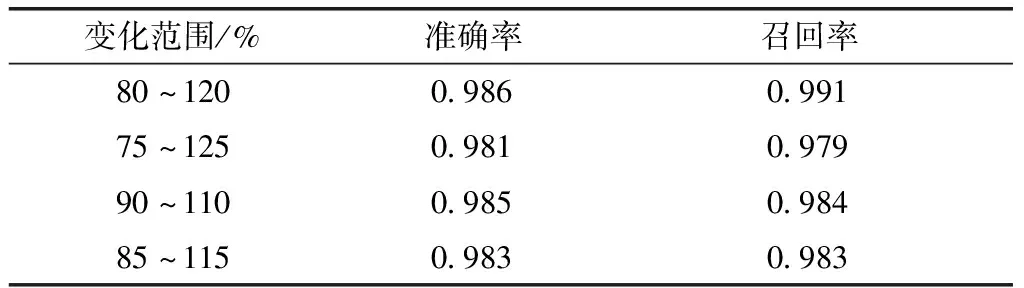
表5 不同发电机/负载功率分布变化测试

(3)负载特性变化。设I为恒电流负载占比，Z为恒功率负载占比，其余为恒阻抗负载。不同负载特性变化下的测试结果如表6所示。

表6 不同负载特性变化测试

根据图6、表5、表6可知，所提出的TSA综合模型能够为电力系统多变的运行环境提供理想的预测精度，并证明了该模型具有较强的泛化能力。

5.1.6 鲁棒性分析

由于设备故障、测量数据的远距离传输等，可能导致引入数据噪声或异常值，实际中评估模型需具备较强的鲁棒性。在测试中，通过在样本集中添加不同数目的无关特征来评估TSA综合模型的鲁棒性，添加无关特征的数目分别为50、75、100、125、150，其中所添加的无关特征为高斯白噪声，相应的测试结果如图7所示。

根据测试结果(图7)可知，添加无关特征确实会影响评估的精确性，但在添加无关特征数目为150个时，TSA综合模型的准确率为0.965、召回率为0.963，仍然具有可接受的预测精度，表明TSA综合模型具备较好的鲁棒性。这是由于TSA综合模型在基于mRMR的特征选择过程中，能够剔除了无关特征，并选择出关键特征用于模型的训练和测试，这能一定程度上减少了数据噪声对预测结果的影响。另外，在训练中所采用的排序提升方法也有助于对抗样本集中的异常值[17-18]。

图7 不同无关特征下的测试结果

5.2 某省级电力系统

为了进一步验证论文所提评估方法的有效性，将TSA综合模型应用于某省级电力系统，该系统包含2 036条母线、149台发电机、761条交流输电线路和1条直流输电线路，其500 kV主网框架图如图8所示。在实际区域电力系统中，大多数停电事故通常与特高压输电线路和超高压输电线路有关，而低压输电线路故障对整个系统的暂态稳定性影响相对较小[19]。因此，选取电压等级在500 kV及以上的线路、母线进行仿真，采用5.1节所述方法生成离线样本，并从该系统上收集到8 862个样本。

图8 某省级电力系统500 kV主网框架图

5.2.1 TSA综合模型的构建

使用mRMR算法分别选取出不同数目的关键特征重复试验，确定最佳的关键特征数目。经过多次试验，当选取350个关键特征时，能达到最佳的评估精度。在生成不同的关键特征集数目时，其相应的评估准确率如图9所示。

由图9可知，在IEEE 39节点系统上，设置5个及以上的mRMR特征选择过程(m≥5)准确率能达到0.995以上；在某省级电力系统上，设置为7个及以上的mRMR特征选择过程(m≥7)准确率能达到0.987以上。在实际应用时，可供其他类似规模的电力系统参考。因此，在某省级电力系统上设置成7个mRMR特征选择过程(m=7)，筛选出7组关键特征集分别训练7个CatBoost模型，并将这7个离线训练模型结合构建TSA综合模型。

图9 生成不同关键特征集数目的评估准确率

5.2.2 性能测试

将80%的样本用于训练，20%的样本用于测试，采用5倍交叉验证法重复实验，取5次测试结果的平均值。对于SVM模型、DT模型、DNN模型、XGBoost模型和单个CatBoost模型，则使用原始样本进行性能评估测试。各个模型的测试结果如表7所示。

表7 某省级电力系统上的测试结果

某省级电力系统的高复杂性增加了TSA的难度，同时直流输电线路的运行也使系统的动态特性发生了根本性变化[12]。因而，与IEEE 39节点系统上的测试结果相比，各个模型在某省级电力系统上的评估精度均有所降低。总体而言，TSA综合模型的评估精度仍高于其他模型，其准确率分别比SVM模型、DT模型、DNN模型、XGBoost模型和单个CatBoost模型提高了0.041、0.046、0.019、0.027、0.015，同时召回率也分别提升了0.044、0.049、0.02、0.031、0.012。因此，与其他模型相比，TSA综合模型更能满足在线TSA的实际需求。