协作机器人关节力矩传感器的设计与研究*
2022-02-28崔建伟
金 源, 崔建伟
(东南大学 仪器科学与工程学院,江苏 南京 210000)
0 引 言
协作机器人需要对机器人的关节输出力矩进行精密测量才能通过人机交互完成路径规划和安全控制[1,2]。目前机器人关节输出力矩的测力方法主要包括:1)电机电流法[3],该方法通过测量电机驱动电流估算关节力矩,其测量精度不高;2)模块化关节力矩传感器法[4,5],通过增加力矩传感器模块,可以精确测量关节力矩,但传感器敏感原件刚度低,会直接影响机器人的刚度和运动精度。注意到协作机器人常用谐波减速器作为动力传动的主要部件,文献[6]研制了一种内嵌于谐波减速器的扭矩传感器,具有较高的灵敏度和精度,但由于柔轮的裙边变形复杂,需在谐波减速器的柔轮上粘贴16组应变片,这样不仅加大加工难度而且使得机器人关节内部走线更为复杂。文献[7]研制了一种具有力感知功能的谐波减速器,相比于文献[6]极大地减少了应变片数目,但需额外设计静、动导电环以解决柔轮走线缠绕问题,并且结构复杂、电气可靠性低。
针对目前研究存在的弊端,本文设计了一种基于谐波减速器柔轮应变的关节力矩传感器,建立了力矩关系模型,完成了样机研制,并进行了性能测试。
1 力矩传感器设计
1.1 传感器结构设计
协作机器人谐波减速器的结构如图1所示,主要包括波发生器、柔轮和刚轮。其中,柔轮固定,波发生器与驱动电机同步旋转,刚轮作为动力输出。柔轮具有良好弹性体的特征,适合作为应变式力矩传感器的敏感元件。采用两组45°双丝栅应变片构成测量精度较高的全桥电路,两组应变片按180°间隔粘贴在柔轮的外侧面。
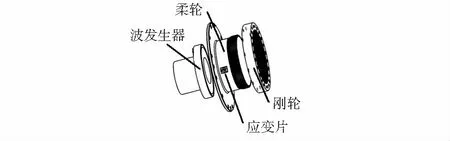
图1 谐波减速器结构
机器人关节内部结构如图2所示。应变片接线可沿着柔轮外延部分的端面固定引出,不会发生缠绕。该结构的优点是:1)与文献[6]相比,大幅度减少应变片数目,降低加工难度;2)与文献[7]相比,无需增加动、静导电环设计,解决柔轮走线缠绕问题;3)与模块化关节力矩传感器相比,直接将谐波减速器的柔轮作为力矩传感器的敏感元件,不影响机器人关节的刚度;4)与电机电流法相比,具有更好的测量精度。
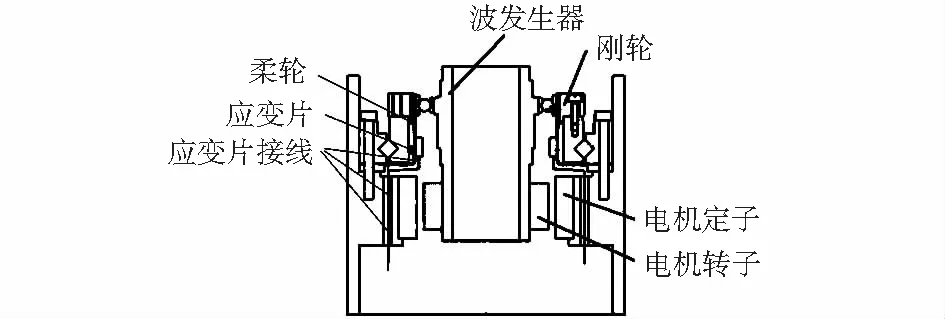
图2 机器人关节内部结构
1.2 柔轮应变的分析与建模
谐波减速器柔轮上的应变包含了因力矩载荷作用而产生的力矩应变和因柔轮椭圆变形而产生的椭圆应变。
1)柔轮力矩应变分析
将柔轮视作圆柱薄壳时,根据圆柱壳体理论可知,柔轮在承受的力矩载荷T时产生的剪应力τ为
(1)
式中r为柔轮的半径,s为柔轮的壁厚。
如图3所示,A为柔轮外表面上的一个被测点,根据材料力学知识可知,在被测点与柔轮轴线夹角为45°和135°的方向上,被测点受到最大拉应力σ1与最大压应力σ2,其值与剪应力相等即
σ1=-σ2=τ
(2)
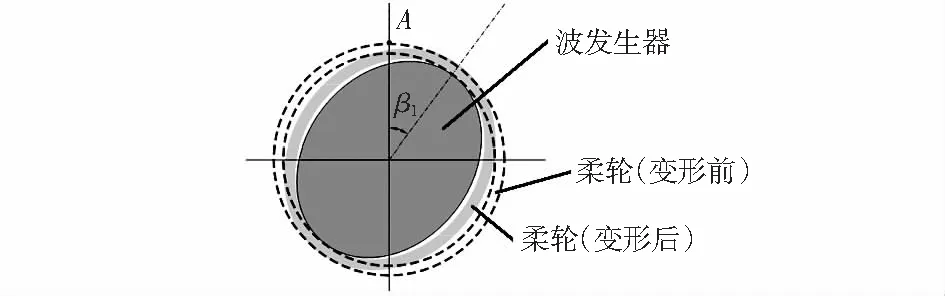
图3 被测点A示意
根据广义胡可定律和式(1)、式(2),被测点的主应变也就是柔轮力矩应变值为
(3)
式中E为弹性模量,μ为柔轮材料的泊松比。
2)柔轮椭圆应变建模
如前图3所示,柔轮由于椭圆形波发生器装入而产生变形。波发生器每旋转一圈,其长轴2次挤压柔轮,使得柔轮上的被测点强制变形2次,故柔轮变形周期fF2倍于波发生器的旋转周期fW,其表达式为
fF=2fW=nW/30
(4)
式中nW为波发生器旋转转速,r/min。根据柔轮椭圆变形的周期,可假设椭圆应变为
ε′=a+bcos(ωFt)
=a+bcos(2ωWt)=a+bcos(2βW)
(5)
式中ωF为柔轮椭圆变形的角频率,ωW为波发生器旋转的角频率,βW为波发生器旋转的角度。a为由于波发生器与柔轮装配而引起的基础椭圆应变,为常量值。bcos(2βW)为波发生器旋转而产生的应变,是柔轮椭圆应变的主要组成分。
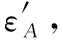
(6)
2 数据处理方法
2.1 数据处理流程
如图4所示为一组典型的柔轮力矩信号。
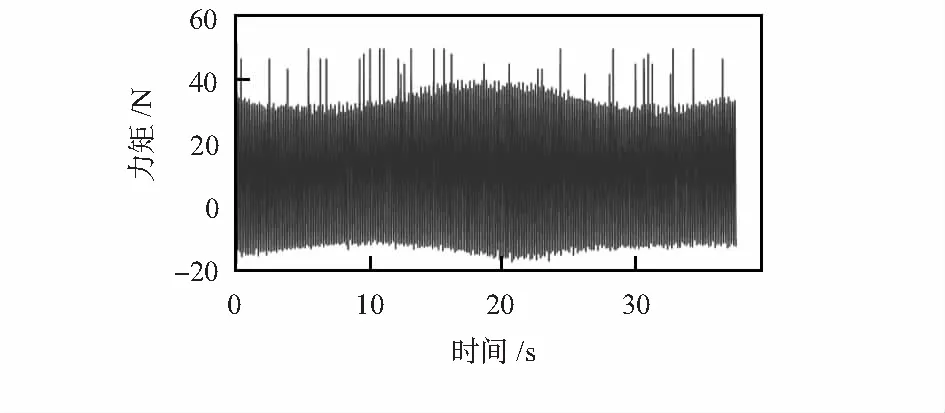
图4 一组典型的柔轮力矩信号(波发生器转速200 r/min)
柔轮椭圆应变对柔轮力矩信号的输出产生较大了影响。为此设计了数据处理方案从而剔除椭圆应变对测量的影响,其主要流程如下:
1)剔除粗大误差:利用莱以特准则去除柔轮力矩数据中的粗大误差。由于受到负载力矩以及电机转速的影响,柔轮力矩数据样本标准差较大,莱以特准则无法很好识别明显的粗大误差。为此,可通过缩小莱以特准则的判别阈值,将残差大于1.8倍标准差的数据即认为是粗大误差,来提升粗大误差的识别率。剔除粗大误差后的柔轮力矩数据如图5所示。
2)频域变换:利用离散傅里叶变换对柔轮力矩信息进行频谱分析。如图5所示的数据进行离散傅里叶变换结果如图6所示。
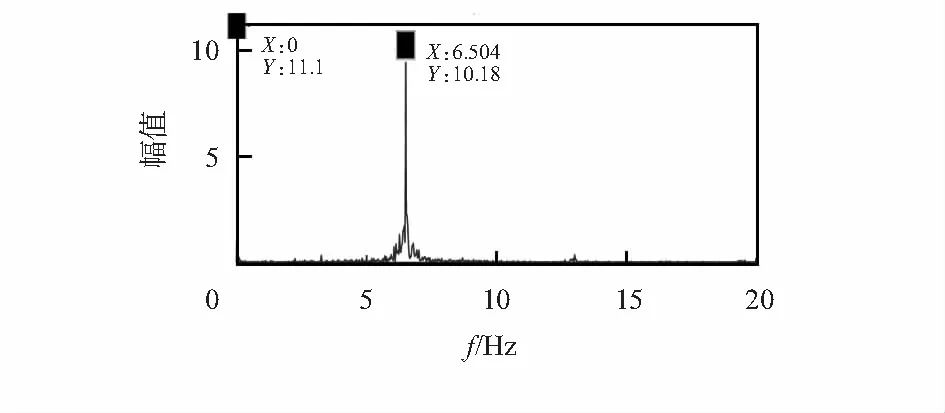
图6 力矩波动信号傅里叶变换示意
根据式(4),当波发生器转速为200 r/min时,柔轮力矩信号频率的理论值为6.666 Hz, 实际测得的柔轮力矩信号频率为6.504 Hz。考虑到误差的存在,可认为频域分析结果证实了确实存在频率为波发生器旋转频率2倍的椭圆应变。
3)滤波:设计了一个I型切比雪夫低通数字滤波器用于滤除柔轮力矩信号中的非直流分量。确定滤波器的通带截止频率为1 Hz,阻带截止频率2 Hz, 通带纹波不超过0.1 dB,阻带衰减至少20 dB。从图7可以看出,柔轮力矩数据通过该数字滤波器后,频率为6.477 Hz交流分量已经被数字滤波器成功滤除。
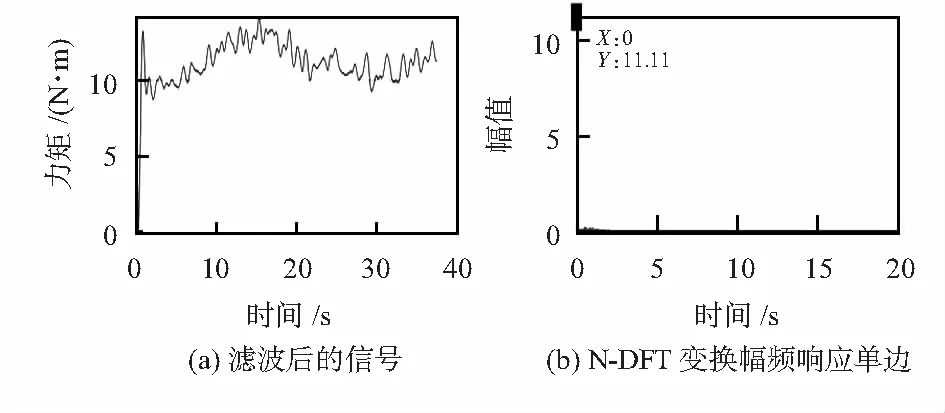
图7 经过滤波后的谐波测力力矩数据
2.2 力矩关系模型的建立
频域分析结果显示柔轮力矩数据的直流分量幅值反映了柔轮在受到负载力矩时发生变形的均值,其柔轮力矩数据的直流分量幅值与负载力矩关系如图8所示。
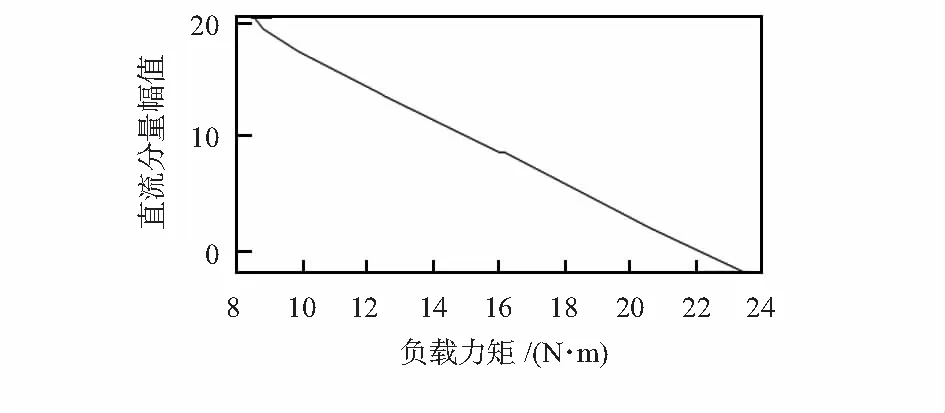
图8 负载力矩和直流分量幅值之间的关系
为此,可利用直流分量幅值与关节负载力矩之间存在线性关系的特性建立柔轮力矩关系模型。定义实际负载力矩T=Ttest-T0。其中,Ttest为标准力矩传感器在负载条件下测量值,T0为标准力矩传感器空载条件下测量值。定义直流分量变化值N=N0-Ntest。其中,N0为空载条件下柔轮力矩数据的基础直流分量幅值,Ntest为负载条件下柔轮力矩数据的直流分量幅值。至此,直流分量幅值变化值N与实际负载力矩T呈正相关关系,即N∝T。
3 实 验
研制的关节力矩传感器测试实验在如图9所示的实验平台样机上进行。调节磁粉制动器的驱动电压,可为实验平台提供不同的负载力矩,标准力矩传感器用于测量实际负载力矩的大小从而与柔轮力矩数据进行标定拟合。两路采集控制仪表分别采集标准力矩传感器数据与柔轮力矩数据。所有性能测试实验均在波发生器以200 r/min速度转动的条件下进行。

图9 实验平台实物
通过空载实验测得柔轮力矩数据的基础直流分量幅值N0为18.224 5,试验台空载力矩T0为7.888 5 N·m。负载实验共测试了9种不同负载条件下柔轮力矩数据输出,其数据如表1所示。
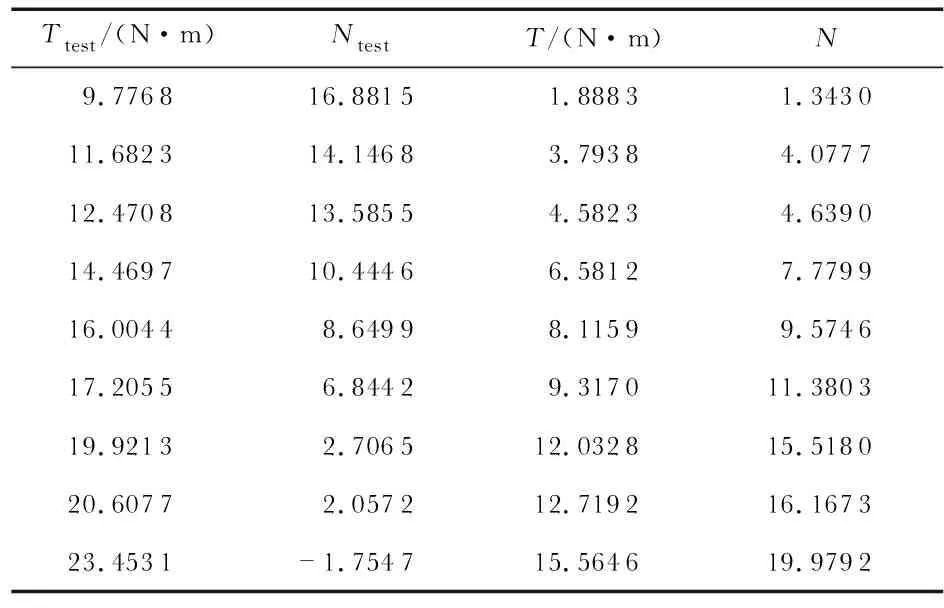
表1 负载实验数据
对柔轮力矩数据进行一次多项式最小二乘拟合处理,建立柔轮力矩直流分量幅值变化值n与实际负载力矩的拟合表达式为
t=0.725 6n+1.013 3
因此,关节力矩传感器的灵敏度为
K=ΔN/ΔT=0.725 6 N·m
关节力矩传感器与拟合力矩值的最大差值发生在实际负载力矩为4.582 3 N·m时,其值为ΔL=0.233 6,故谐波测力减速器的非线性度为
谐波测力减速器的重复实验共进行2次,其测量数据如表2所示。
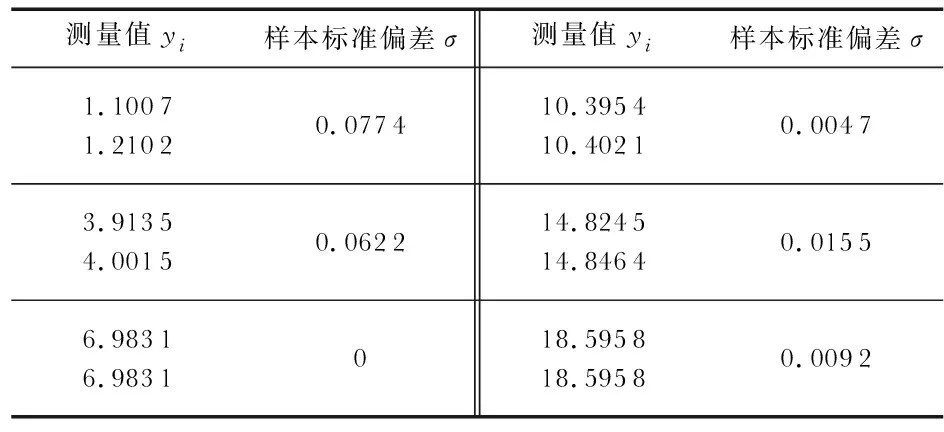
表2 重复实验数据
根据谐波测力减速器重复性计算公式,取置信系数a=2,置信概率为95.4%,得到谐波测力减速器的重复性为
4 结束语
基于柔轮应变测量的关节力矩传感器的研制,在提升协作机器人人机交互性方面具有重要的意义。研制的关节力矩传感器的灵敏度为0.725 N·m,重复性可达0.99 %。通过更多的数据处理算法对柔轮力矩信号进行分析以提高关节力矩传感器的可靠性和精度是下一步研究的方向。
