改进鸽群优化算法在SVD-UKF参数整定中的应用*
2022-02-28周延锋李宁洲卫晓娟王卫红
周延锋, 李宁洲, 卫晓娟, 王卫红
(1.兰州交通大学 机电工程学院,甘肃 兰州 730070; 2.上海应用技术大学 轨道交通学院,上海 201418;3.株洲九方装备股份有限公司,湖南 株洲 412001)
0 引 言
近年来,鸽群优化(pigeon-inspired optimization,PIO)算法因其结构简单、易于理解以及较强的全局搜索能力而受到诸多学者的广泛关注[1,2]。但其易陷入局部最优,且收敛速度较慢。文献[3]将鸽群优化思想引入粒子滤波算法,通过在鸽群优化过程中加入自适应交叉操作来增加粒子多样性,提高了粒子滤波算法的求解精度。郭瑞[4]通过引入收敛因子、位置因子以及速度因子来增强鸽群活力、提高种群多样性,扩大了潜在解的搜索空间。文献[5]提出了一种基于A*和鸽群算法的航路规划算法,实现了对航路进行平滑化和重规划处理。文献[6]将混沌优化与迭代步长动态调节策略相结合,对混沌变量和优化变量进行映射操作,提高了算法的收敛速度与局部搜索能力。文献[7]通过引入自适应权重系数,对种群个体的速度和位置进行更新,提升了航路规划质量和效率。
为进一步加快PIO算法的收敛速度,提升全局搜索能力及局部收敛精度,本文在指南针算子中融入天牛须搜索(beetle antennae search,BAS)算法来增大潜在解的搜索空间,在地标算子引入Kent混沌扰动策略来提高局部搜索能力及收敛精度,通过测试函数和奇异值分解—无迹卡尔曼滤波(SVD-UKF)参数整定的仿真实验检验改进效果及可行性。
1 PIO算法
受鸽群飞行导航方式启发,段海滨教授提出了PIO算法,其数学模型包括指南针算子和地标算子两部分[7,8]。
首先引入指南针算子,对于D维目标搜索空间中的优化问题,每个鸽群个体i代表一个可行解,其位置和速度可分别表示为:Xi=(xi1,xi2,…,xiD),i=1,2,…,N,Vi=(vi1,vi2,…,viD),i=1,2,…,N,其中,N为鸽群规模,即所有可行解的个数。在第k次迭代中,鸽群个体的速度Vi及位置Xi根据下式进行更新
Vi(k)=Vi(k-1)*e-Rk+r1(Xg-Xi(k-1))
(1)
Xi(k)=Xi(k-1)+Vi(k)
(2)
式中R为指南针因子,r1为[0,1]上的随机数,Xg全局最优解。
在地标算子中,每迭代一次,鸽群规模N减半,适应度较优的50%鸽群的中心位置Xc作为鸽群个体飞行的参考方向,鸽群个体的更新方式如下
N(k)=N(k-1)/2
(3)
(4)
Xi(k)=Xi(k-1)+r2(Xc(k)-Xi(k-1))
(5)
式中F(•)为鸽群个体重量,解决最小优化问题时F(•)=1/f(•)+ε,ε为一个很小的数,针对最大优化问题时F(•)=f(•),r2为[0,1]上的随机数。
2 改进的PIO算法
2.1 指南针算子改进
BAS算法作为一种新型仿生算法,其数学原理表述如下:
1)假设天牛随机向任何方向前进,即右触须指向左触须的矢量可使用随机向量进行表示,对其进行归一化处理可得
(6)
式中D为空间维度。
2)天牛质心为X,d0为两触须间距离,则左右触须位置可表示为
(7)
3)确定左右触须气味强度f(Xl)和f(Xr),进而判别天牛前进方向。
4)结合天牛的搜索行为,天牛位置的迭代更新方式为

(8)
式中Xk为第k次迭代中的天牛质心,Xl(k-1),Xr(k-1),δk-1分别为第k-1次迭代中的左右触须位置及步长。
5)更新步长公式如下
δk=δk-1η
(9)
式中η为步长衰减系数。
循环步骤(1)~步骤(5),即可获得全局最优解。因此,在指南针算子中,基于BAS算法对PIO算法进行改进的基本思路是当鸽群个体位置与速度更新之后,将其视为天牛,计算其按照BAS算法移动之后的适应度值,并对移动前后的适应度值进行对比,如果移动后的适应度值更优,则移动,否则不进行移动。
2.2 地标算子改进
混沌作为一种非线性动力学现象,在搜索空间具有很强的遍历性。为提高算法的局部搜索精度,在地标算子中引入混沌扰动策略,以获得相对较优的鸽群个体。
本文采用遍历性较好的Kent混沌映射,其数学模型为
(10)
式中Zn为混沌变量。
地标算子中,鸽群个体位置的更新方式由其适应度值决定,适应度值较优的前N/2个个体采用原方式更新,适应度值较差的后N/2个个体采用引入混沌扰动的方式更新,更新方式具体如下
(11)
式中β(k)为调节系数,Zi为第i个鸽群个体的混沌变量。
综上所述,改进的PIO(IPIO)算法流程为:
Step1 初始化鸽群规模N、指南针算子迭代次数Nmap、地标算子迭代次数Nland、指南针因子R、鸽群个体的速度V和位置X;初始化两触须距离d0、步长δ、衰减系数η。
Step2 根据式(1)、式(2)更新鸽群个体速度Vi(k)及位置Xi(k),然后根据式(6)~式(8)更新天牛位置XiBAS(k),根据式(9)更新步长。
Step3 比较天牛移动前后的适应度值f(Xi(k))和f(XiBAS(k)),选择适应度值较优个体作为更新后的鸽群个体,更新全局最优解Xg。
Step4 判断是否k>Nmap,是则执行下一步,否则返回Step2。
Step5 根据式(3)、式(4)计算鸽群数目和鸽群位置中心,根据式(11)更新鸽群个体位置,进而更新全局最优解Xg。
Step6 判断是否k>Nland,是则结束程序,输出全局最优解Xg,否则返回Step5。
3 基于IPIO算法的SVD-UKF参数整定
无迹Kalman滤波(UKF)因其滤波求解精度较高等优点在诸多领域得到了广泛地应用[9]。但其采用的Cholesky分解无法对非正定矩阵进行分解,易造成病态问题。为避免这一问题,增强协方差矩阵的数值稳定性,可利用求解性能较好的奇异值分解(SVD)对Cholesky分解进行替换。
SVD-UKF的参数主要有:过程噪声协方差矩阵Q,观测噪声协方差矩阵R以及尺度系数ρ。以往参数的设定主要依赖主观经验,估计效果不佳。因此,本文将结合机车黏着控制工程背景,利用IPIO算法对SVD-UKF的参数进行整定。参照文献[10],SVD-UKF观测器的状态方程及观测方程分别如下
(12)
(13)
式中Tm为牵引电机转矩,TL为牵引电机负载转矩,Jequ为轮对侧等效转动惯量,Rg为齿轮箱传动比,ωw为轮对角速度。
通过分析可知,Q为二维对角阵,而R和ρ均为常数,故IPIO算法的寻优个体可构造为Xi=(q1,q2,R,ρ),4个参数作为IPIO算法的适应度变量。寻优问题适应度函数的选择常依据其性能进行选择,本文选择动态响应速度较快、超调量小的时间误差积分准则ITAE,所构造IPIO算法适应度函数的数学表达式为
(14)

4 仿真实验
4.1 算法性能测试
为验证IPIO的正确性及有效性,将其与PIO及PSO算法进行对比分析。所选性能测试函数为Rosenbrock、Sphere、Griewangk以及Rastrigin,其均在(0,…,0)点处取得全局最小值0。为保证测试结果的公平性及科学性,对其均进行以下参数设置:种群/粒子群数量N=50,最大迭代次数k=1 000,个体/粒子维数D=20,将其各自独立运行30次的最优值及最优值的平均值和方差作为测试结果。4种测试函数的表达式及变量取值范围如下
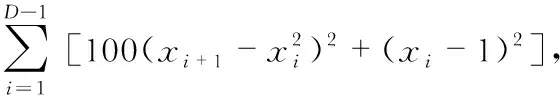
xi∈[-30,30],

xi∈[-600,600]
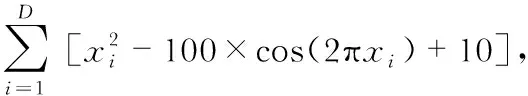
xi∈[-5.12,5.12]
三种算法对4种性能测试函数的寻优结果见表1,适应度收敛曲线如图1~图4所示。

表1 测试函数寻优结果
由表1可知,针对单峰函数,对于函数f1,IPIO的最优值分别比PIO和PSO高6个和3个数量级,平均值分别高于4个和1个数量级;对函数f2,只有IPIO的最优值为0,其平均值和标准差也远远高于PIO和PSO。
针对多峰函数,对于函数f3,只有IPIO的寻优最优值为0,平均值和标准差也均优于PIO和PSO;而对函数f4,仍只有IPIO的最优值为0,且平均值和标准差也均高于其他两种算法8~9个数量级。
由图1~图4可以看出,IPIO算法总能够迅速地收敛,其收敛速度均远高于PIO和PSO,证明对指南针算子的改进有效提升了其全局收敛速度。从表1的实验结果也可以看出,由于Kent混沌扰动策略的融入,地标算子的局部搜索能力及搜索效果也得到了显著的提升。通过以上分析,均证实了本文对PIO所提出改进策略的可行性及有效性,为后期的参数整定奠定了基础。
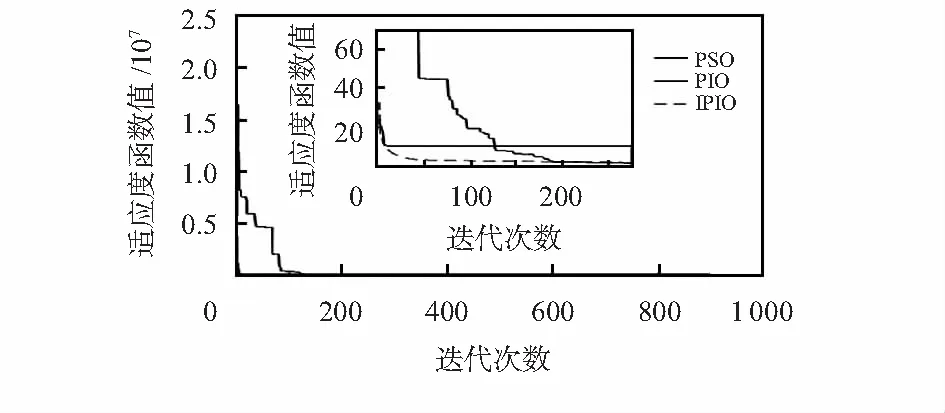
图1 f1函数的适应度收敛曲线
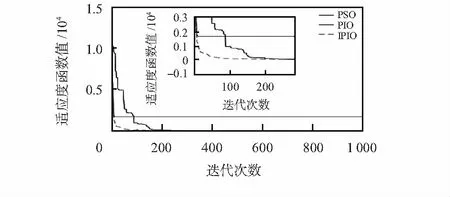
图2 f2函数的适应度收敛曲线
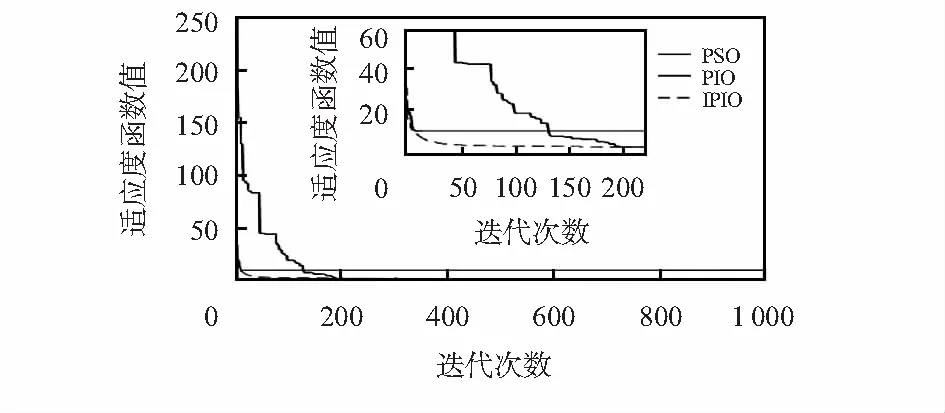
图3 f3函数的适应度收敛曲线

图4 f4函数的适应度收敛曲线
4.2 SVD-UKF参数整定
采用IPIO算法脚本文件调用机车单轮对SIMULINK模型的方式,对SVD-UKF参数进行整定,机车动力学参数设置:车轮半径R为0.625 m,轴重W为25 000 kg,齿轮箱传动比Rg为5.64,齿轮箱传递效率ηgear为0.95,车轮侧等效转动惯量Jequ为184.9 kg/m3。
以式(14)作为适应度函数进行寻优,获得一组最适合的参数(q1,q2,R,ρ)来满足机车黏着控制过程中的观测需求。算法参数设置为:N=30,Nmap=90,Nland=30,R=0.3,d0=2,δ=π,η=0.95。基于此,优化整定后的SVD-UKF参数为(8.420 1×10-6,9 189.474,0.01,1.001 5),SVD-UKF参数优化整定过程中的适应度函数收敛曲线如图5所示。
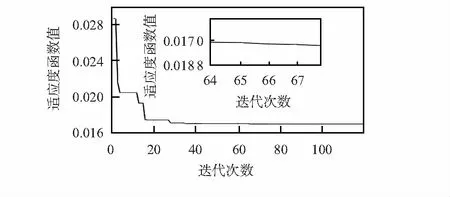
图5 SVD-UKF参数整定适应度函数收敛曲线
从图5可以看出,IPIO算法在SVD-UKF参数优化整定过程中,适应度函数收敛速度较快,在迭代次数30次左右时,已收敛至全局最小值附近,表明改进算法在SVD-UKF参数整定时亦具有较优的搜索性能。
黏着系数估计对比分析如图6所示。机车运行过程中,轨面工况在5 s时进行切换,从图6中可以看出,参数优化整定前的黏着系数估计效果并不理想,对轨面实时黏着系数的估计存在滞后现象。而参数优化整定后的SVD-UKF响应速度较快,在不同的轨面工况下,均能够对轨面实时黏着系数进行有效估计,跟踪效果较好,为机车黏着的有效控制及提高其黏着利用率提供了保障。

图6 黏着系数估计对比分析
5 结 论
针对PIO算法易陷入局部最优、收敛速度较慢的缺点,提出了融合天牛须算法与混沌扰动策略的改进方式。通过性能测试函数验证了IPIO算法的可行性及有效性。并将经IPIO优化整定后的SVD-UKF应用到机车黏着控制中,仿真结果表明:在不同工况下SVD-UKF均具有良好的估计效果,所提出的适应度函数也能够有效地对观测器的滤波估计效果进行定量评估。
