基于Maklink路径规划混合定位算法研究*

杨俊磊, 段倩倩

(上海工程技术大学 电子电气工程学院, 上海 201620)

0 引 言

路径规划是平面上从源点出发经若干节点到达目标终点求最短路的优化问题。在路径规划中,常用算法分为全局和局部两种，其中,全局路径规划算法有Dijkstra算法、A*算法、粒子群算法、蚁群算法等[1～4]。机器人无碰撞避开障碍物的路径规划是当前学者研究的热点问题之一，研究学者常用栅格法作为机器人路径规划的地图模型，不能较好体现实际地形的复杂多样性。

目前，路径规划广泛应用于工厂物资输送，应急车辆避障救援等，这些问题不仅要保证行驶路径最优，时间短，配送效率高，还需要规避障碍物[5,6]。何成伟等人应用Maklink图构建无向网络障碍物模型，保证规划的自动导引车(automatic guided vehicle,AGV)路径沿着凸多边形边缘行走不会与真实的障碍产生碰撞，但实验研究较为单一，不能体现复杂障碍物环境的多样性[7]。王飞等人利用Graham算法生成凸多边形并向外扩展h的安全距离，确保飞机航线不与障碍物发生碰撞，但航线路径需要遍历所有节点，增加了搜索时间，规划路径非全局最优[8]。粒子群算法、蚁群算法等[9，10]具有良好的寻优能力、算法精度高、收敛快等优点，广泛应用于路径规划问题中，并通过迭代寻找最优解。其中，粒子群算法通过适应度函数评价路径解，但算法容易陷入早熟，局部寻优解较差。黄超等人[11]通过融合蝗虫算法的粒子群算法改善收敛速度。文献[1]采用广度优先法对遍历节点进行扩展并选出距源点最近节点作为扩展节点，但随着遍历节点增多，Open表节点排序时间消耗较大，计算效率较低。文献[12]通过无线传感器节点定位算法对锚节点精确定位，继续扩展未知节点，定位过程中，盲节点定义为所需定位的未知节点。

针对上述学者研究成果及存在的不足，本文提出了一种混合节点定位算法(hybrid node localization algorithm,HNLA)，在不同规模地图环境中有效减少了遍历节点及迭代次数，节省了搜索时间并规划出最短路径。

1 相关工作介绍

1.1 粒子群算法

粒子群算法是Kennedy J和Eberhart R在1995年根据群鸟和鱼群的成群性质提出的一种启发式算法[13]。粒子群提供搜索算法的初始种群，粒子会随时间改变它们的位置，并在优化系统中根据经验选择最佳位置Pi，全局最佳位置Pg以及搜索速度Vi。粒子速度更新根据Vid=w×Vid+c1×r1×(Pid-Xid)+c2×r2×(Pgd-Xgd)，其中，w表示惯性权重；c1和c2为常数，r1和r2为随机函数，其值都∈(0,1)；粒子位置根据Xid=Xid+Vid更新，Xid表示粒子i在d维搜索位置。

1.2 蚁群算法

蚁群算法[14]求解路径规划问题主要根据信息素浓度更新以增强蚁群信息素的浓度值，提高收敛速度。通过轮盘赌法并根据概率公式(1)判断并选择下一节点

(1)

式中α为访问各城市节点的程度因子，β为转移到最近城市的程度因子，τij(t)为蚂蚁从节点i到j释放的信息素浓度总量，ηij(t)=1/dij为节点间路径期望值，dij为节点之间距离，allow为待遍历的节点集，信息素更新如下

τij(t+1)=(1-ρ)·τij(t)+Δτij(t)

(2)

(3)

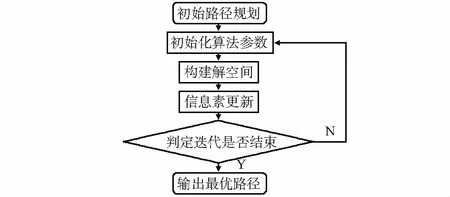
图1 蚁群算法解决TSP流程图

2 混合定位方法策略

2.1 区域分割

2.1.1 确定段节点

根据文献[15]构建Maklink线规划初始参考节点对障碍物区域进行分割,并将参考节点作为相应分割区域的段节点。图2为初始段节点及分割区域，其中,V1，V2，…,V7为初始段节点。

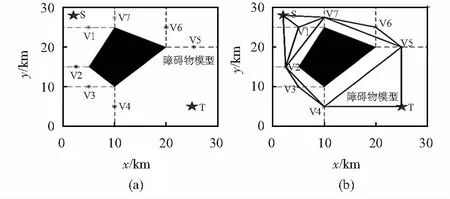
图2 初始段节点及分割区域

2.1.2 区域分割

通过确定的段节点进行路径搜索，将区域进一步分割：

Step1 将初始节点坐标S作为搜寻盲节点的质心坐标(xn,yn)。

Step2 由式(4)确定同段区域距离质心最远的盲节点Am作为分割区域的搜索节点，式(5)确定第g段盲节点区域

(4)

(5)

式中m为盲节点数，dAm,Aj和dAm,Ai为Am与邻近盲节点Aj距离及Am同其他盲节点Ai距离。若dAm,Aj≤dAm,Ai，将节点Aj加入到Am，作为段节点新的搜索位置;反之，继续区域分割。

Step3 盲节点位置确定：1)在每次区域所分割的段中计算出已知节点到不同段中段节点的距离以及与同段中其它节点的距离;2)计算不同段中节点之间的最小距离差

(6)

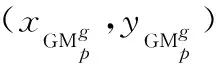
Step4 直到所有段节点区域分割完毕，停止。

2.2 盲节点边界定位

根据先前步骤计算得到的段节点，确定盲节点位置边界。应用文献[16]包围盒技术的方法计算矩形边界，通过dAm,Ai和已知节点位置(xAi,yAi)计算矩形边界，如图3所示。由已知段节点Am,A2,A3及dAm,Ai,dAm,Aj确定盲节点所在位置，根据式(7)和式(8)计算盲节点位置的边界框Ei以及边界框的相交面积Sj

Ei=[xAi-dAm,Ai,xAi+dAm,Ai]×

[yAi-dAm,Aj,yAi+dAm,Ai]

(7)

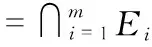
(8)

式中 矩形区域中心坐标为(xSi,ySi)，长为dAm,Ai×(1-sinθ),宽为dAm,Ai-dAm,Ajsinφ,m为盲节点数，其中,1≤i≤m。

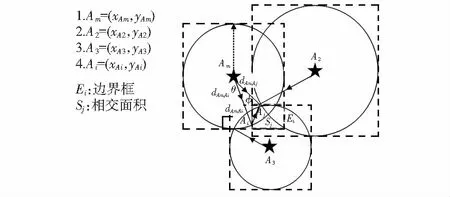
图3 盲节点边界定位

2.3 混合算法设计

为确保盲节点定位正确性和计算速度，使其预计位置接近最短路径上的实际位置，本文采用粒子群和蚁群相结合的混合动态算法规划路径。通过最佳节点所在位置pbk,每段最佳节点所在位置plS,全局所在最优位置gb来提高搜寻速度并对盲节点定位。根据式(9)适应度值作为距离和算法收敛速度的衡量标准

(9)

式中 (xAi,yAi)为节点Ai位置；dAm,Aj为节点Am到不同区域段中盲节点Aj的距离；m为节点数量。第k只蚂蚁的搜索位置和速度根据式(10)、式(11)求解

vk(t+1)=w(t)vk(t)+c1r1(pbk-xk(t))+

c2r2(gb-xk(t))+c3r3(pls-xk(t))

(10)

xk(t+1)=xk(t)+vk(t+1)

(11)

(12)

式中w=0.7，c1=c2=c3=1.494，ri∈[0,1],Lup和Ldown为从边界框中获得的局部化区域边界，t为蚂蚁所在最佳位置的不变时间，t′ 为区域边界更新时间。采用粒子群算法提高搜索速度，搜索最佳节点位置，计算当前段最短路径节点之间长度Lij，根据式(2)更新该条路径上节点信息素

(13)

根据式(1)计算Pij，找出最优遍历节点，迭代完成后，规划出最短路径L*。改进算法流程如图4所示。

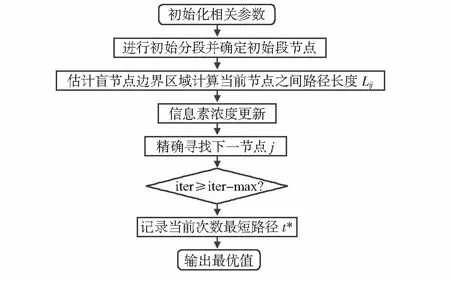
图4 改进算法流程图

3 实验仿真与分析

为了验证改进算法的有效性，在实验平台为Intel®CoreTMi5—4210U CPU@2.40GHz，4.00GB RAM，软件环境为 Windows 10专业版，MATLAB2016a中编程实现对文献[1，7]和改进算法路径规划，实验模拟真实避障环境，对比分析了路径长度、扩展节点、搜索时间以及迭代次数。

3.1 实验仿真

构建实验区面积为50 km×50 km，100 km×100 km,200 km×200 km的不同规模障碍物空间。目标起点分别为S1(5,10)km，S2(10,90)km，S3(20,180)km对应目标终点T1(45,45)km，T2(90,15)km，T3(160，90)km，寻找一条从起点S到终点T的最优路径。蚁群算法相关参数设置，蚂蚁个数为35，信息素因子α为1.6，启发式因子β为5，挥发因子ρ为0.2，信息素总量Q为50，最大迭代次数为NC=500。基于上述参数设置，采用Maklink图构建段节点，进行初始区域分割，划分段节点以及定位节点，如图5所示。

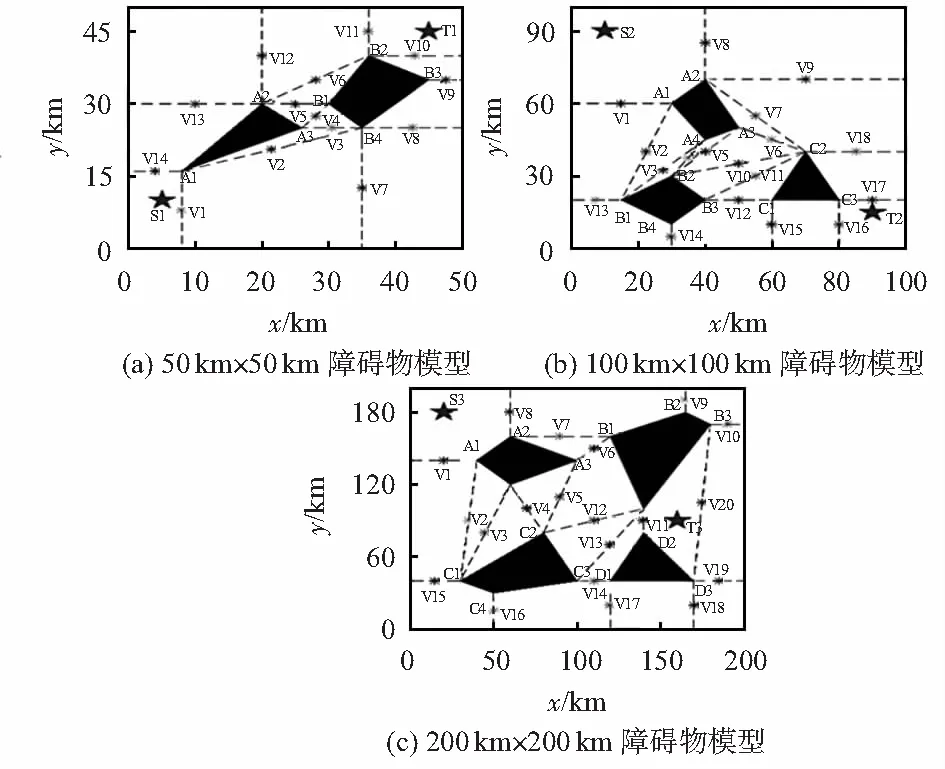
图5 初始区域分割

3.2 实验结果分析

通过实验研究，随着障碍物模型增加，路径复杂度增加，相应分割区域、段节点随之增加。图6和图7为文献[1]、文献[7]和改进算法路径规划结果以及在不同规模下迭代次数与适应度值变化曲线。

图6(b)中点划线为改进算法优化路径，实线为文献[1]算法优化路径，虚线为文献[7]算法优化路径，三种算法实验结果对比见表1。从图6(b)及表1得出，在不同规模障碍物下，改进算法收敛速度比文献[1]、文献[7]算法都快，规划路径长度最短；采用文献[2]路径比的方法衡量三种算法路径规划的效率，实验表明，改进算法在规避障碍物上搜索全局路径效果比其他两种算法路径更优。

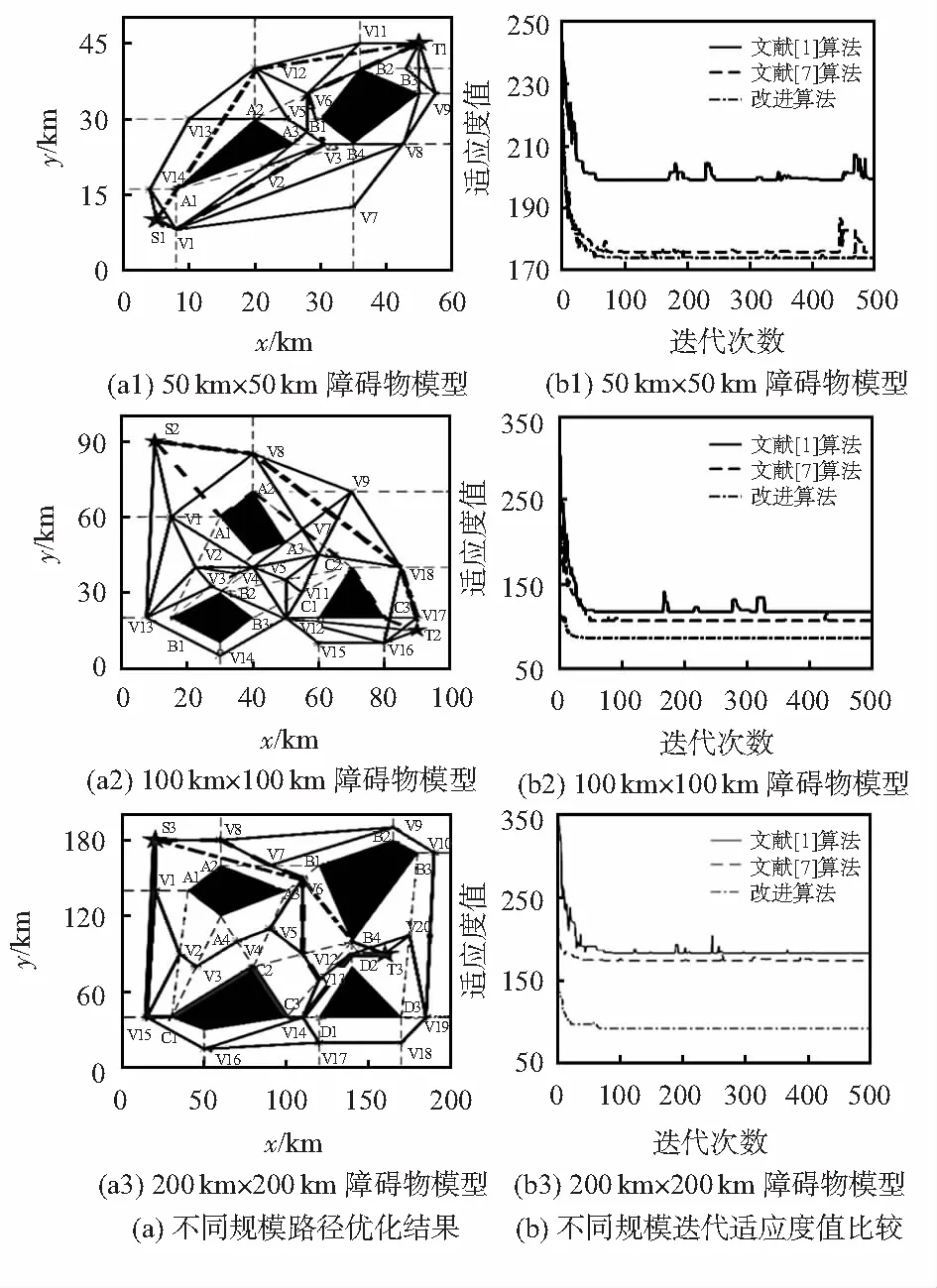
图6 实验结果

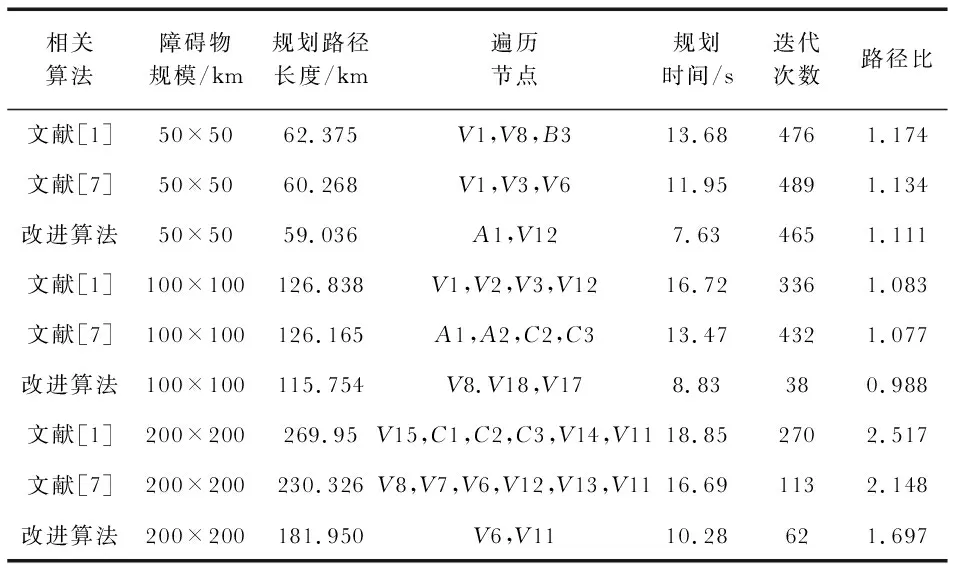
表1 实验结果对比

4 结束语

随着路径规划障碍物规模增大，文献[1]和文献[7]算法在问题解精度以及收敛速度上存在不足。提出加快搜索速度、精确节点定位的改进算法，对节点所在位置精确估计，求解最优路径。实验结果表明：改进算法的最优解精度以及收敛速度优于其他两种算法，当障碍物规模、复杂度增大时，改进算法节点定位的有效性更加突出。在后续研究中，将在不同规模障碍物的三维环境下，研究改进算法的求解精度以及收敛性。