新型双面交叉T型沟槽碳化硅中子传感器*

董翰林， 于成浩， 郭浩民， 韩运成， 张立龙

(1.杭州电子科技大学 电子信息学院，浙江 杭州 310018； 2.中国科学院合肥物质科学研究院，安徽 合肥 230031)

0 引 言

中子探测问题一直受到空间探索、国土安全、核电站、高能物理实验等领域的高度关注[1～3]。碳化硅(SiC)中子传感器的抗辐射能力远优于硅或锗传感器[4]。并且与3He正比计数管相比，SiC中子传感器具有工作电压低、电荷收集快、体积小、中子伽马判别能力强等优点[5]。由于中子是电中性的，用于识别中子的方法通常依赖于中子和转换材料(6LiF，10B)发生核反应产生的次级带电粒子[6]。当这些带电粒子进入SiC二极管的有源区时，通过库仑散射产生多个电子—空穴对，最终通过外电极对电子和空穴进行收集便可获得微小的电流脉冲信号，从而便间接地实现对中子的探测[7]。

已有几个研究小组在结构参数设计以提高本征检测效率方面做出了实质性的早期贡献[8]，由于中子转换材料的自吸收作用，薄膜涂层中子传感器的探测效率低于5 %[9]。为了提高中子探测效率，研究人员开发了叠层硅中子传感器[10]。此外，堪萨斯州立大学还开发了硅微结构半导体中子探测器(microstructured semiconductor neutron detector,MSND)[11]。目前，大多数研究都集中在SiC薄膜涂层中子传感器上，而关于SiC微结构中子传感器的报道很少[12]。

1 单面型SiC中子传感器

1.1 平面型SiC中子传感器的仿真分析

平面型SiC中子传感器由中子反应膜和SiC二极管器件组成，如图1(a)中的插图所示。常用的中子转换材料有6LiF和10B，而中子与6LiF反应产生的带电粒子能量更高，更容易将中子信号从伽马背景噪声中区分出来。中子先与6LiF发生反应产生2.05 MeV的α粒子和2.73 MeV的氚粒子，为了保持动量守恒，α粒子和T粒子向着相反的方向出射。基于蒙特卡洛技术[13,14]的Geant4工具包可以逐步追踪这些粒子，直到它们失去全部能量或离开世界体。由于中子捕获概率随着转换层厚度t的增加而增加。然而，由于转换材料对次级带电粒子的自吸收效应，导致次级粒子将其能量沉积在转换材料中，而对输出脉冲信号没有贡献。如果转换器层很厚，则导致次级粒子的能量沉积在转换层中，而无法到达SiC二极管区域。因此，转换层厚度在平面型传感器的设计中至关重要。通过将低能甄别阈值(low energy level discrimination threshold,LLD)设置为300 keV便可以滤除掉Gamma背景的干扰，因此中子探测效率便可以定义为在SiC传感器区域中沉积能量大于LLD的事件数除以入射到传感器的中子事件数。探测效率和能量淀积谱随转换层厚度t的变化分别如图1(a)和图1(b)所示。

图1 平面型SiC中子传感器

从图1可以看出，当转换层的厚度小于或大于最佳厚度时，探测效率都会下降。很明显，当6LiF 的厚度达到25 μm左右，本征检测效率达到最大值4.3 %，然后随着6LiF厚度的增加，探测效率缓慢下降。这种现象是因为限制热中子本征探测效率的两个因素是中子吸收效率和反应产物逸出概率。当转换层较薄时，中子被俘获的概率较小，因此次级粒子的数量较少。当转换层较厚时，由于转化材料对次级粒子的自吸收增强，反应产物逸出的概率降低。这从能量淀积谱图中同样可以发现当6LiF的厚度较薄时，在2.05 MeV附近可以观察到明显的α峰，在2.73 MeV附近可以观察到明显的T峰。这是因为次级粒子通过薄转换层仅损失少量能量，因此大部分可以进入SiC传感器。当6LiF的厚度继续增加到40 μm时，高能区间的计数减少，而低能区间的计数增加。这主要是由于转换层的自吸收效应增强，这也不利于区分背景伽马射线。由于次粒子向着相反方向喷射，每次核反应后，只有一个次级粒子可以进入 SiC 传感器区域，因此，可以发现图1(b)中的能量截止值是能量最高的次级粒子的能量值。

1.2 沟槽型SiC中子传感器的仿真分析

由于转换材料的自吸收效应，平面型SiC中子传感器的本征探测效率被限制在5 %以下。幸运的是，如图2(a)所示的沟槽型微结构中子传感器可以突破这一限制。因为沟槽型SiC中子传感器可以增加6LiF的填充量和次级粒子入射到SiC区域中的概率。影响沟槽型SiC中子传感器的本征探测效率的结构参数有沟槽间隙Tg,沟槽宽度Tw和沟槽深度H。

对于用6LiF 回填的沟槽型MSND，任意选择沟槽宽度Tw为20 μm。当LLD=300 keV时，沟槽型MSND在不同沟槽深度H下本征探测效率随沟槽间隙Tg的变化如图2(b)所示。可以发现，随着沟槽间隙Tg的增加，本征探测效率先急剧增加，然后缓慢下降。当沟槽间隙Tg约为5 μm时，无论沟槽深度H如何，本征探测效率都取到最大值。接着当沟槽深度H固定为100 μm，当LLD=300 keV时，本征探测效率随沟槽间隙Tg变化，如图2(c)所示。可以发现，当沟槽宽度Tw取不同的值时，沟槽间隙Tg为5 μm时本征探测效率总是达到最大值且与沟槽宽度Tw无关。

基于上述结论，对于6LiF回填的MSND，最优的沟槽宽度Tg可以固定为5 μm。并且随着沟槽宽度Tw的增加，探测效率先升高后降低。如图2(d)所示，在不同沟槽深度H的情况下，当沟槽宽度Tw约为15 μm时，本征探测效率均达到最大值。因此，6LiF回填的MSND的最佳参数组合是15 μm的沟槽宽度Tw和5 μm的沟槽间隙Tg。

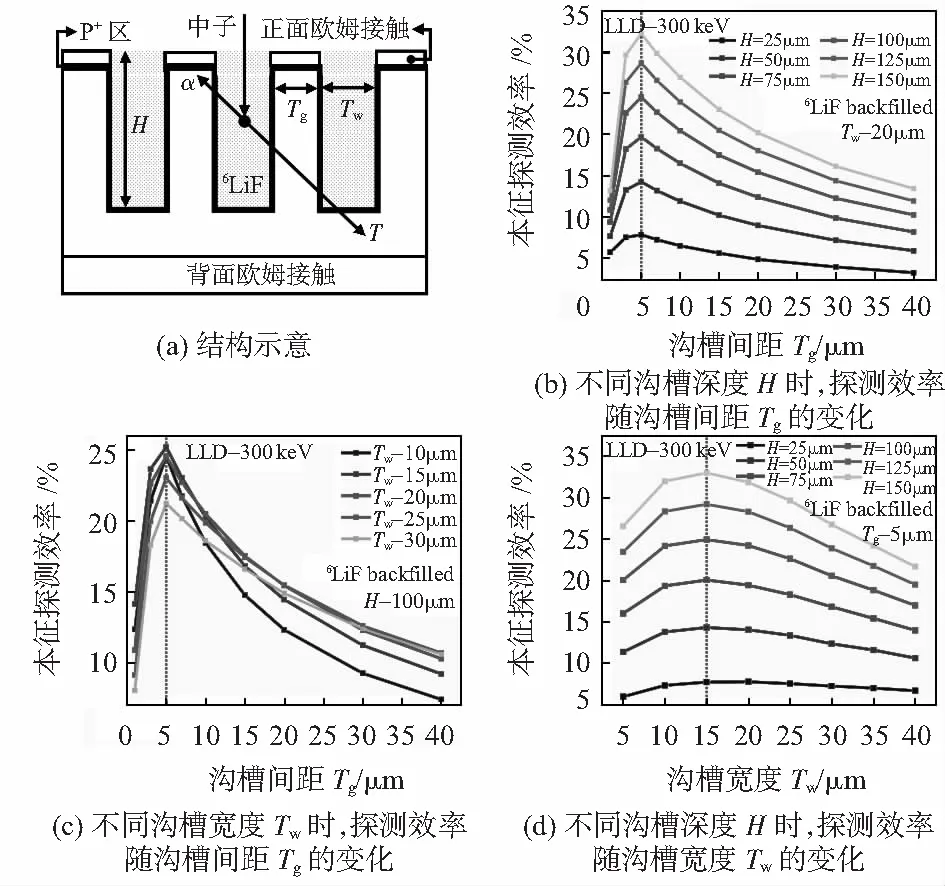
图2 沟槽型SiC中子传感器

2 双面沟槽型SiC中子传感器

2.1 新型双面交叉式T型沟槽结构

为了进一步提升器件的性能，已有团队提出了双面蚀刻的交叉式微结构如图3(a)所示[15]。尽管制造起来更加困难，但电场将在整个检测器区域中均匀分布，并且收集所有产生的电荷所需的信号积分时间将减少，并且不受增加的微结构深度的限制。但由于中子经过SiC区域将不能被吸收，因此存在中子的自由流通路径，不利于探测效率的提升。本文提出了一种新型双面交叉式T型沟槽结构的SiC中子传感器如图3(b)所示。该结构可以完全消除中子自由流通路径，可以提升中子吸收概率进而可以大幅度提升器件的中子探测效率。同样兼具电场均匀和信号积分时间短等优点。

图3 两种结构示意

2.2 结果对比分析

传统的双面交叉式微结构中子传感器需要在4H-SiC外延片的正面和反面分别进行交叉式的沟槽刻蚀，需要往正面和背面的沟槽内部都回填中子转换材料6LiF。而双面交叉式T型沟槽结构中子传感器可以在4H-SiC外延片的正面和反面通过两次曝光和两次刻蚀后形成交叉式的T型沟槽，可以进一步增加SiC刻蚀深度。然后在双面T型沟槽内分别形成P区和N区，接着将T型沟槽内回填满中子转换材料。本文提出的T型沟槽SiC结构相较于传统的交叉指型中子传感器可以完全消除中子自由流通路径，进而可大幅提升中子探测效率。当沟槽深度H为100 μm时，采用蒙特卡洛软件Geant4对两种结构的中子传感器的本征中子探测效率随着LLD的变化情况如图4(a)所示。交叉型结构的探测效率随着LLD的变化较小，而双面T型沟槽的探测效率随着LLD的变化减小很快，当LLD大于800 keV后，探测效率低于传统的交叉型。但是实际中的Gamma射线或者背景噪声在SiC中淀积的能量一般都在300 keV以下，因此，将LLD设置为300 keV时，就完全可以消除掉背景噪声或者Gamma射线引入的误计数。双面T型沟槽型中子探器件相比于传统交叉指型传感器件，中子探测效率提升了7.23 %。显然，T型沟槽中子传感器可以大幅度提升中子探测效率。而且从SiC实际的工艺出发，100 μm的刻蚀深度是很难实现的[16]。而本文提出的T型沟槽可以通过两次刻蚀就很容易实现100 μm的刻蚀深度。

此外，由于SiC材料的P区和N区只能使用离子注入形成，但是深沟槽的底部和侧壁离子注入形成连续的P区和N区难度很大，而本文提出的T型沟槽结构可以只在上沟槽部分使用离子注入形成部分的P区和N区掺杂，如图4(b)所示的结构。这样也有助于提高器件的电荷收集效率,可以进一步提升器件的性能。

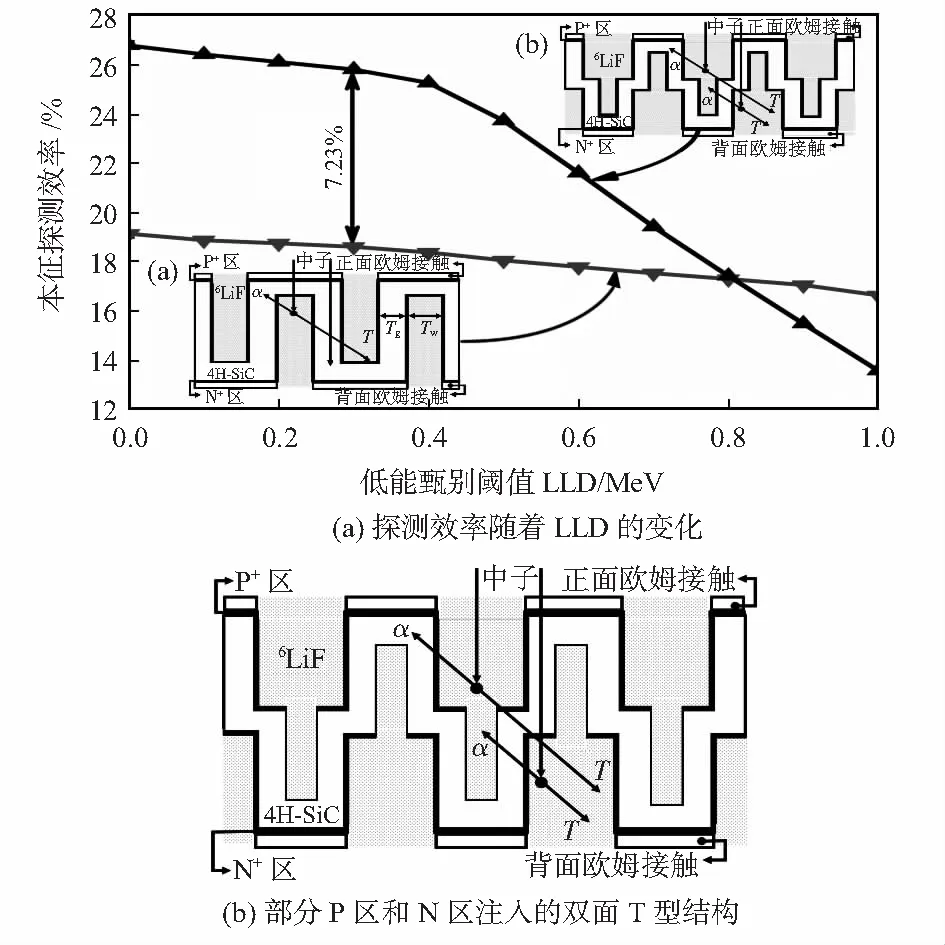
图4 两种结构探测效率对比结果分析

3 结 论

由于中子是电中性的，用于识别中子的方法通常依赖于次级带电粒子。本文中，基于Geant4工具包研究了基于SiC的中子传感器的性能。考虑了薄膜涂层和沟槽型中子传感器，并根据相关结构参数计算了它们的本征探测效率，LLD值固定在300 keV。由于转换材料的自吸收效应，薄膜涂层SiC中子传感器的本征探测效率被限制在5 %以下。沟槽型SiC中子传感器可以突破这一限制。基于传统的交叉型沟槽结构提出新型双面T型沟槽结构，可以完全消除中子自由流通路径进而显著提高中子的本征探测效率。并且本文提出的T型沟槽结构可以只在上沟槽部分使用离子注入形成部分掺杂的P区和N区。这样也有助于进一步提高器件的电荷收集效率进而提升器件的性能，为以后深沟槽高性能SiC中子传感器的制造提供了方案。