指数函数及其反函数图象公切线方程的表示

北京丰台二中 甘志国 （邮编：100071）

有很多文献给出了指数函数与其反函数图象公共点个数的结论，特别是拙文[1]还给出了关于x的方程ax＝logax的根的表示.通过网络搜索可知，尚无文献研究指数函数及其反函数图象公切线方程的条数.当指数函数y＝ax中的a已知时，本文的定理给出了这方面的完整结论，并且还给出了所有公切线方程及切点坐标的表示，在表示方法中除一步用到了求增函数的反函数外其他步骤是底数是e的乘方、求对数或与常数的四则运算.

定理设曲线y＝ax与曲线y＝logax的公切线条数是ω（a），则

（1）当 0＜a＜e-e时 （若 函 数Γ（t）＝则存在唯一的正数α使得a＝e-eΓ（α）），ω（a）＝3，在同一条公切线上的两个切点均不重合，三条公切线分别是

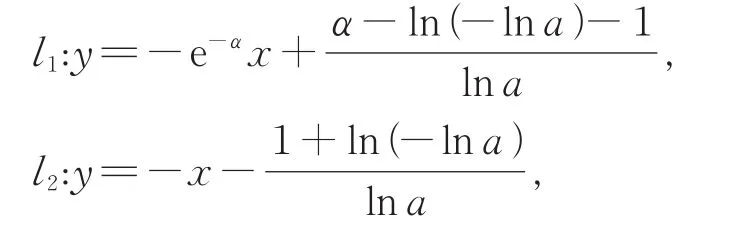
l3:y＝-eαx-（它们的斜率依次成非常数列的负项等比数列，l1、l3关于直线y＝x对称）；它们与曲线y＝ax分别切于点（它们的横坐标xA、xB、xC满 足xA+xC＝2xB＝-logaln2a，纵坐 标yA、yB、yC满 足与曲线y＝logax分别切于点C*、B*、A*（它们分别是三点A、B、C关于直线y＝x的对称点）；

（2）当a＝e-e时 ，ω（a）＝1，公 切 线 方 程 是，两个切点重合，均是

（3）当 e-e＜a＜ 1 时，ω（a）＝1，公切线方程是y＝-x-loga（-elna），它与曲线y＝ax，y＝logax的切点分别是它们不重合）；

（6）当a＞时 （若 函 数则存在唯一的正数β，使得a＝eeΩ（β）），ω（a）＝2，这两条公切线关于直线y＝x对称（它们的斜率均是正数且互为倒数），在同一条公切线上的两个切点均不重合，两条公切线分别是l1:y＝e-βx+它们与曲线y＝ax分别切于点（它们的横坐标xA、xB满 足xA+xB＝-2logalna，纵坐标yA、yB满足时，ω（a）＝0；

（5）当时，ω（a）＝1，公切线的方程是y＝x，两个切点重合，均是（e，e）；yAyB＝），与曲线y＝logax分别切于点B*、A*（它们分别是两点A，B关于直线y＝x的对称点）.

证明设曲线y＝ax与曲线y＝logax的公切线l与它们分别切于点由导数的几何意义可得公切线l的斜率k＝aulna＝，所以

还可设公切线l的方程是y＝kx+m，由点A，B均在公切线l上，可得

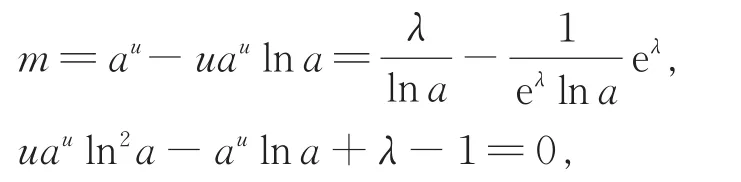
设 lna＝b（a≠ 1）即a＝eb（b≠ 0），再设函数f（λ）＝bλeλ-beλ-λ-lnb2-1，可得公切线的条数ω（a）即函数f（λ）的零点个数.

（Ⅰ）当b＜ 0，即 0 ＜a＜ 1时.

当t＞ 0时，可得Γ（t）＞t-1，所以当t＞ 0时，Γ（t）的值域是（1，+ ∞ ）.

因而偶函数Γ（t）在 （-∞，0），（0，+ ∞ ）上分别是减函数、增函数，值域是（1，+∞）.

可设b＝-eμ-λ，a＝e-eμ-λ，进而可得

f（λ）＝0⇔（λ-1）（eμ-1）＝-2μ⇔μ＝0或λ＝1-或Γ（μ）＝μ-λ

（i）当 0 ＜a＜ e-e即μ-λ＞ 1时，可得存在唯一的正数α使得a＝e-eΓ（α）（再由a＝e-eμ-λ可得μλ＝Γ（α）＞ 1），所 以f（λ）＝0⇔μ＝0或Γ（μ）＝Γ（α）⇔μ＝α，0，-α

⇔λ＝α-Γ（α），-Γ（α），-α-Γ（α）⇔

进 而 可 得 结 论 （1）成 立 ，由a＝e-eΓ（α）可证得进而可得直线l1与l3关于直线y＝x对称.

（ii）当a＝e-e即μ-λ＝1时，由Γ（μ）＞ 1，可得f（λ）＝0⇔μ＝0⇔λ＝-1，进而可得结论（2）成立.

（iii）当 e-e＜a＜1 即μ-λ＜1 时 ，可 得，进而可得结论（3）成立.

（ⅠⅠ）当b＞ 0即a＞ 1时.

再由Ω（0）＝-1，及当t＞0时-1＝t-3，可得偶函数 Ω（t）在 （-∞，0]，[0，+∞）上分别是减函数、增函数，值域是[-1，+ ∞ ），当且仅当t＝0时，Ω（t）min＝-1.

可设b＝eμ-λ，a＝eeμ-λ，进而可得

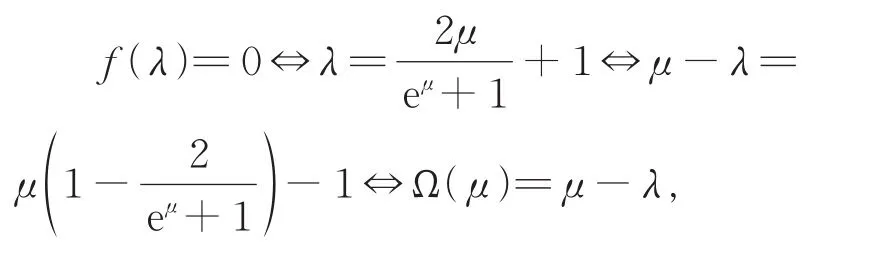
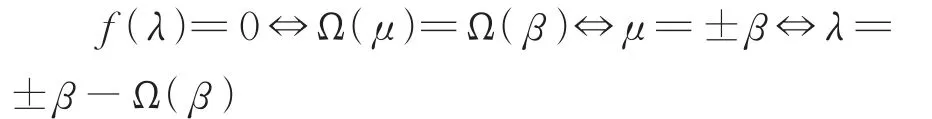
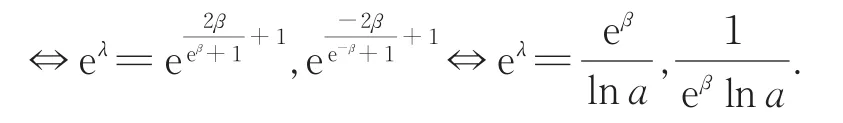
进 而 可 得 结 论 （6）成 立 ，由a＝eeΩ（β）可证得进而可得直线l1与l2关于直线y＝x对称.

注 在定理（1）中，可得α＝Γ-1（ln （-lna））（其中Γ-1（t）是函数Γ（t）（t＞ 0）的反函数）；在定理（6）中，可得β＝Ω-1（lnlna）（其中 Ω-1（t）是函数Ω（t）（t＞ 0）的反函数）.因而，当a已知时，定理给出了曲线y＝ax与曲线y＝logax的所有公切线方程及切点坐标的表示，在表示方法中除一步用到了求增函数的反函数外其他步骤是底数是e的乘方、求对数或与常数的四则运算.

推论1若曲线y＝ax与曲线y＝logax的公切线与它们的切点重合，则a＝e-e（此时公切线条数是1，方程是（此时公切线条数是1，方程是y＝x，切点是（e，e））.

证明由定理可得欲证结论成立，下面再给出其直接证明.

可设a＝eλ（λ≠ 0），重合的切点是由导数的几何意义可得公切线的斜率k＝λeλev＝

f′（v）＝在 （-∞，0），（0，+∞）上 均 是 增 函 数.再 由f（±1）＝1，可 得v＝±1.

当v＝-1时，可得λ＝-e，a＝e-e，重合的切点是公切线的斜率k＝-1，公切线的方程是

当v＝1时，可得重合的切点是 （e，e），公切线的斜率k＝1，公切线的方程是y＝x.

推论 2（1）（i）函数有且仅有两个零点，且这两个零点互为倒数（设为

（ii）曲线y＝lnx与曲线y＝ex有且仅有两条公切线（其中α1同（i）），且l1，l2与曲线y＝lnx分别切于点与曲线y＝ex分别切于点

（ii）曲线y＝ex与曲线y＝lnx有且仅有两条公 切 线l1:y＝eβ1x-β1-1，l2:y＝e-β1x+β1-1（其中β1同（i）），且l1，l2与曲线y＝ex分别切于点（β1，eβ1），（-β1，e-β1），l1，l2与曲线y＝lnx分别切于点 （e-β1，-β1），（eβ1，β1）.

证明由定理（6）及f（α）＝0 ⇔ Ω（-lnα）＝0（见函数 Ω（t）定理（6））可得该结论成立，下面再给出其直接证明：

易证得g（β）是奇函数，所以g（β）有且仅有两个零点且这两个零点互为相反数.

再由

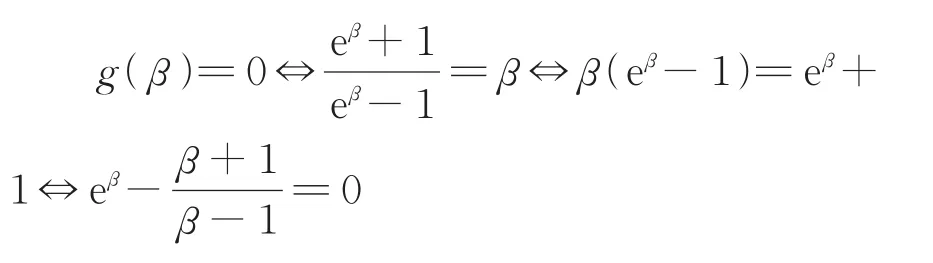
又 可 证 得f（α）＝0⇔g（-lnα）＝0（其 中f（α）见（1）（i）），可得欲证结论成立.

（ii）设曲线y＝ex与曲线y＝lnx的公切线l与它们分别切于点A（u，eu），B（v，lnv），由导数的几何意义可得公切线l的斜率，所以v＝e-u.

还可设公切线l的方程是y＝kx+m，可得

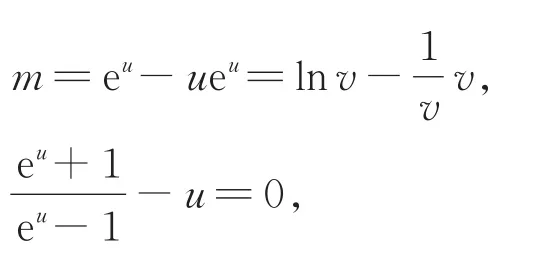
再由（i）的结论，可得欲证结论成立.

（1）由 （2）（i）中 证 得 的f（α）＝0 ⇔g（-lnα）＝0，β1＝-lnα1及结论（2），可得欲证结论成立.

题1（2018年高考天津卷理科数学第20题）已知函数f（x）＝ax，g（x）＝logax，其中a＞1.

（1）求函数h（x）＝f（x）-xlna的单调区间；

（2）若曲线y＝f（x）在点 （x1，f（x1））处的切线与曲线y＝g（x）在点 （x2，g（x2））处的切线平行，证明

题2（2019年高考全国卷ⅠⅠ文科第21题）已知函数f（x）＝（x-1）lnx-x-1.证明：

（1）f（x）存在唯一的极值点；

（2）f（x）＝0有且仅有两个实根，且两个实根互为倒数.

题3（2019年高考全国卷ⅠⅠ理科第20题）已知函数

（1）讨论f（x）的单调性，并证明f（x）有且仅有两个零点；

（2）设x0是f（x）的一个零点，证明：曲线y＝lnx在点A（x0，lnx0）处的切线也是曲线y＝ex的切线.

注题1～3的背景均是本文开头的定理——指数函数及其反函数图象的公切线问题：

（i）由定理的证明可给出题 1（3）的比参考答案要简洁的证法.

（ii）题 2（2）的结论即即题 3（1）的后半部分结论也推论 2（1）（i），由推论 2（1）（ii）可得题 3（2）的结论.

问题 1（1）试求曲线y＝ex+a与曲线y＝lnx-a的公共点个数λ（a）与公切线条数μ（a）；

（2）试求曲线y＝ex+a与曲线y＝ln（x-a）的公共点个数λ（a）与公切线条数μ（a）；

（3）试求曲线y＝aex与曲线的公共点个数λ（a）与公切线条数是μ（a）.

问题2试求曲线y＝ax与曲线y＝logbx的公共点个数λ（a，b）与公切线条数μ（a，b）.