考虑运输碳税与质量承诺的多式联运路径优化

陈维亚，龚浩，方晓平

(中南大学 交通运输工程学院，轨道交通大数据湖南省重点实验室，湖南 长沙 410075)

降低多式联运成本和提高多式联运服务质量是树立并强化“中国物流”优质服务形象的关键环节。在国家深化交通运输供给侧结构性改革的决策部署下，低碳多式联运提速行动提上日程[1]。碳税和碳交易是当前世界主要的2种减排政策，虽然我国尚未直接开展碳税试点工作，但相关研究和政策制定都在积极开展[2]。在未来运输碳税征收下，探究多式联运经营者会如何综合考虑碳税和服务质量承诺决策多式联运路径，对政策制订和经营决策均具有参考意义。针对多式联运路径优化问题，以往主要侧重从多式联运经营者角度寻找考虑质量的最优路径和考虑低碳的最优路径。考虑服务质量方面，SUN等[3-4]分别建立了时间和费用最小的优化模型，求解时间和需求不确定性下的联运路径决策；刘杰等[5]将货物运到期限加入优化模型的约束条件，求解使货物能够在客户要求的时间内运抵目的地的成本最小路径；张得志等[6]考虑运输时间、中转时间以及客户对货物到达的时间要求，建立了基于时效性的多式联运协调优化模型；梁晓慷[7]考虑模糊运输时限时间窗，以运输费用最小、客户满意度最高为优化目标，构建多式联运路径优化问题的线性规划模型；裴骁等[8]以提高联运所有参与者的综合满意度为目标，研究中欧集装箱多式联运路径优化问题。考虑碳排放方面，JΙANG等[9]研究了具有二氧化碳减排目标及污染排放的多式联运网络问题；SADEGHEΙH等[10]在运输问题中考虑了碳税对企业造成的成本影响，建立数学模型通过遗传算法进行求解；QU等[11]将非线性整数规划模型线性化，在考虑碳排放的基础上分析了单一运输方式与多式联运方案的成本变化；蒋琦玮等[12]将运输时间、转运时间设为随机数构建多式联运机会约束模型，并将碳排放内化为成本对运输方案进行规划；李玉民等[13]研究了多式联运过程中运输时间、费用、碳排放的多目标路径优化问题。现有文献多数单一考虑最小化碳排放量或碳排放税，或单一考虑运到期限约束，少数同时考虑了碳排放和运到期限，大多忽略了联运全程的货损质量，未见研究者综合探究考虑运输碳税时运到期限、货物完好程度质量指标变化时联运路径以及各项成本的变化。本文基于运输碳税征收的假设，从联运经营者决策角度，构建综合考虑运到时限、货物完好程度2个运输质量承诺和运输碳税征收的集装箱多式联运路径优化决策模型。模型引入模糊运到时间[14]以及随机货损率2个质量承诺表征变量，将运到时限超限和货损转化为时间补偿成本和货损补偿成本，将碳排放转换为联运经营者的运输碳税，将三者内化为多式联运经营者的总成本组成，并通过案例分析有、无碳税征收2种情形下，不同运到时限和货物完好程度承诺等级对多式联运路径选择的影响。

1 问题描述

多式联运经营者计划将一批重量为w吨的大宗货物通过集装箱多式联运从起点城市O运送至目的城市D，起终点间存在多个转运节点，相邻节点之间具有公路、铁路、水路中一种或多种运输方式可供选择(联运网络示意图如图1所示)，节点间不同运输方式具有不同的运输单价、运输时间、货损率和碳排放水平。为了保持客户满意度，多式联运经营者对联运服务给出质量承诺，如承诺运到时限、货物完好程度等关键质量，并承诺通过补偿方式弥补客户质量损失。因此，本文的研究问题是在考虑运输碳税征收和质量承诺的情况下，寻求某批次货物多式联运总成本最小的最优联运路径。

图1 多式联运网络示意图Fig.1 Schematic diagram of multimodal transport network

2 模型构建

2.1 模型假设

考虑多式联运业务的实际特征，对模型做如下合理假设：

1)同一批多式联运承运货物品类无差异，起终点相同，采用集装箱进行整箱配装运输；

2)相邻2节点之间只能采取一种运输方式；

3)货物在同一节点处的换装中转次数不大于一次；

4)仅考虑运输与中转过程中的货损，忽略不可抗力因素。

2.2 模型变量

定义多式联运网络为G=(I,F,K)，模型的主要参数、变量及符号说明见表1。

表1 集合、参数及决策变量说明Table 1 Description of sets,parametersand decision variables

2.3 目标函数

保证承诺的服务质量水平和控制联运成本是多式联运经营者在进行联运路径优化时考虑的主要目标。本文将运输碳税和服务质量承诺转换为碳税成本和质量损失补偿成本，建立以多式联运总成本最小的目标函数。其中，多式联运总成本主要包括运输成本、中转成本、碳税成本以及服务质量损失补偿成本：

1)运输成本

运输成本CTt为联运路径上所有路段运输成本之和，单个路段运输成本为所采用运输方式的运输单价与运输距离以及货物总重w的乘积，运输总成本由公式(1)计算：

2)中转成本

中转成本CTf是联运路径上节点处货物由运输方式k转换到运输方式l时的换装等中转成本，单个节点的中转成本为货物总重w和单位中转成本c kli的乘积，全程总中转成本由式(2)计算：

3)碳税成本

碳税成本CTa包括在联运过程中的路段运输碳排放税和节点中转碳排放税，计算路段运输与节点中转的碳排放量通过碳税值Cc转化为碳税成本，由式(3)计算：

4)服务质量损失补偿成本

服务质量损失补偿成本CTq是指经营者为了保障承诺的联运服务质量水平，当联运过程中出现服务质量未达到承诺水平时补偿客户损失的成本。本文主要考虑2个关键服务质量指标损失补偿成本，一个是货物提前或延迟到达时的到达时间补偿成本，另一个是货物在运输和中转过程的货损货差赔付成本，由式(4)计算：

式(4)中：TD为货物实际到达的时间；[T1,T2]为货物到达的承诺时间窗。在实际运输过程中，货物发生货损可能有多方面的原因，考虑简化问题，本文仅考虑路段运输随机货损和中转随机货损，随机货损率分别由和θz表示。

综上，模型的目标函数可表述为式(5)：

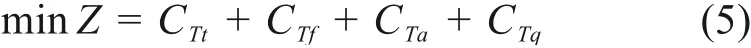
2.4 约束条件

模型考虑的主要约束条件如下：

约束条件(6)表示2节点之间只能采取一种运输方式；约束条件(7)表示在节点处只允许换装转运一次；约束条件(8)表示运输工具的装载能力不能小于货运需求；约束条件(9)保证货物联运路径的连续性；约束条件(10)表示联运全过程货损率满足允许货损率要求；约束条件(11)为运到时间需满足模糊时间窗约束，ε为非负无量纲模糊运到时间系数；约束条件(12)和(13)为0-1决策变量约束。

3 求解算法

本文构建的多式联运路径优化模型实质上是在多约束条件下求解带节点费用的时空网络最短路径问题，无法通过解析精确求解。本文设计改进的遗传算法进行求解，引入精英片段保留策略增强算法的鲁棒性，算法关键步骤描述如下。

第1步 基础数据导入：导入节点间运输距离矩阵D(节点间无直接运输方式时距离为无穷大)、节点转运备选集0-1矩阵B，以及其他基础数据。

第2步 染色体编码：采用运输节点与运输方式相结合的编码方法。确定起终节点编号(1，N)，随机生成长度为X=N的运输节点编码、长度为Y=N-1的运输方式编码，将2段编码合为一段(X,Y)，最终路径方案的染色体表示如图2所示。

图2 染色体编码表示Fig.2 Chromosomecodingrepresentation

第3步 初始化种群：根据模型中设置的约束条件筛选个体进入种群，随机生成个体来代替淘汰个体，保证种群的多样性，并去除重复的个体。

第4步 设计适应度函数：模型为求解总成本最小的单目标最优路径优化问题，总成本为非负值，因此构建基于总成本函数的适应度值Fitness(i)=1/minZ，当总成本越小时，适应度值越大；对适应度值进行排序，根据选择概率GGAP选出一定数量个体组成种群规模。

第5步 染色体交叉：通过交叉概率Pc选择染色体执行2号位单点交叉操作，交叉后检验染色体是否为可行解，若为不可行解则将该点所处的基因片段进行交换。

第6步 染色体变异：通过变异概率Pm随机选择染色体基因片段执行单点变异，基因变异过程引入如图3所示的精英片段保留策略：精英片段保留以运输节点编码为基础，以节点城市1～9为例，针对第t代精英个体为X*t，随机选取X*t中的精英片段M，将下一代个体Xt+1中与片段M中重复的编码删除，然后将M放置在Xt+1编码后端，得到新个体X*t+1。

图3 精英片段保留策略Fig.3 Elitefragmentretentionstrategy

第7步 可行解判断：在交叉变异操作后可能产生不可行解，淘汰不可行解后，从初始种群中随机选择个体进行补充，保证初始种群规模。

第8步 得到满意解：采用最大迭代次数终止运算得到满意解，否则跳到第4步。

4 算例分析

4.1 算例参数

在17个城市节点构成的多式联运网络上，如图4(a)所示，多式联运经营者需要从起点13通过集装箱运输一批重量为800t的货物到达终点16。联运运输方式集合K={1=公路，2=铁路，3=水路}，节点之间可选运输方式见图4(b)。

图4 多式联运网络与运输方式矩阵Fig.4 Multimodaltransportnetworkandtransportmodematrix

参考文献[9]选取不同运输方式及中转的碳排放量，碳税率设为0.15元/kg。运输方式间的中转费用、时间及碳排放和不同运输方式的平均运输速度、运输单价、碳排放量等参数如表2和表3所示。

表2 中转费用(元/t)/中转时间(h)/中转碳排放(kg/t)Table 2 Transfering cost(元/t)Transfering time(h)Transfering carbon emissions(kg/t)

表3 不同运输方式的运输参数Table 3 Transport parameters of different modes of transportation

参考不同运输方式平均货损情况的调查结果[15]，设定不同运输方式的平均货损率分别为每百公里0.01%(公路)、0.015%(铁路)、0.02%(水路)，单次中转平均货损率为0.04%；根据我国对超过0.5%的货损需要向保险公司索赔的要求[16]，让客户进行保险理赔时容易导致客户丢失，因此设定货物完好程度承诺等级为(L1，L2，L3，L4)4级，分别对应4级最大容许货损率，表示为L1(0.35%)，L2(0.4%)，L3(0.45%)，L4(0.5%)；货 物 运 到 小 时的承诺时间窗为[48,72]。

遗传算法操作设置：交叉概率为0.8，变异概率为0.15，选择概率为0.8，种群规模为80。

4.2 结果与讨论

算例主要对比分析有、无碳税征收2种情形下不同运到时限和货物完好程度承诺等级对多式联运路径选择的影响。

表4 展示了模糊运到时间系数ε=0.1、不同货物完好程度承诺等级下，碳税率分别为0和0.15时的联运路径选择结果。相同质量承诺等级内，碳税征收情形下选择的联运路径的总碳排放量均较少；在货物完好程度承诺等级为L1和L2时，运输方式分别选择了公—水、公—铁联运，L3和L4时主要选择了铁—水联运，说明在满足同一运到时限承诺下，随着货物完好程度承诺等级的降低，碳税征收使公路运输比例降低、铁路和水路运输比例增大，货损成本略有增加，联运总成本下降明显。

表4 不同碳税率下联运路径选择的变化Table 4 Changesin transportation schemes under different carbon taxing rates

表5 展示了在碳税率为0.15时，不同货物完好程度承诺等级和模糊运到时间系数组合的联运路径选择结果。同一货物完好程度承诺等级下，相比于总成本，不同运到时限要求引致了较小的运到时间补偿成本差异(L3等级除外)和碳税成本差异，说明运到时限参数设置对算例没有起关键约束作用。相反，货物完好程度承诺等级严格约束了路径选择，高承诺等级引导模型更高比例选择了平均货损率较低的公路运输，导致联运总成本显著增加。

表5 征收碳税情形下不同质量承诺组合的联运路径选择结果Table 5 Change of multimodal transport scheme when the quality commitment changes under carbon taxing

5 结论

1)通过引入模糊运到时间和随机货损率2个表征变量，将货物运到时限和货物完好程度2个关键指标的质量承诺内化为质量损失补偿成本，将联运过程中的碳排放量内化为碳税成本，构建了总成本最小的联运路径优化模型，有利于综合权衡质量承诺和碳税征收对路径选择的影响。

2)算例表明，在相同质量承诺下，碳税征收可引导多式联运经营者选择碳排放更低的联运路径；质量承诺等级越高对经营者选择联运路径的约束越严苛，偏向于选择货损率较低、时效性较高的公路运输，导致联运路径的总碳排放量和总成本越高，给联运企业带来较大的经济负担；因此联运经营者可根据货主的个性化需求灵活多变地选择路径，实现利益最大化。

3)本文考虑运输成本时主要采用了平均运价，可以进一步探讨递远递减的铁路运费等因素对联运路径选择的影响。