固化流态底泥填筑路堤内土体抗剪强度空间变异特性及其影响

韩 超， 柏 彬， 张献蒙， 蒋达飞， 孙 科， 刘寅莹

(1. 国网江苏省电力工程咨询有限公司， 江苏 南京 210036； 2. 华中科技大学 土木与水利工程学院， 湖北 武汉 430074)

随着我国经济建设的快速发展，国家对生态文明建设愈发重视，水域环境治理正在全国范围内如火如荼地开展，由此产生了大量的河湖疏浚底泥。据不完全统计，2016年我国年产疏浚底泥已达5亿m3[1](水下方)，2020年已超10亿m3。河湖底泥是水域中部分生物的主要居住环境，是污染物、垃圾沉淀堆积的重要场所，因此具有有机质含量高[2,3]、重金属含量高[4,5]、难以降解的颗粒杂质多等特点。再加上实际工程中主要采用水力冲挖或绞吸疏浚，所以其中的含水率也较高(整体呈流态，没有强度，下文将其称为流态底泥)，疏浚后的方量也会较之前增大1～3倍，如此大体量的流态底泥其末端处置问题一直困扰着工程界。

针对流态底泥，常用的处理方式有：

(1)作为原料用于制作陶粒、砖、水泥等，但该方式处理能力有限、耗能过高且制成的产品应用范围有限(重金属含量过高)。

(2)存放至疏浚堆场，干化后寻求资源化处理，但该方法占地面积大，干化速度慢，堆场整体周转周期长，并且因为重金属含量较高，会对周围土壤、地下水造成二次污染。

(3)化学固化后作为填筑材料应用于各类填方工程，该方法改善了流态底泥的工程特性[6]，对底泥中的有机质以及重金属进行了有效的固化稳定化[7,8]，降低了二次污染的风险；另外，该方法能够处理大体量的流态底泥，并使其资源化利用，缓解了当前填筑土壤资源不足的困境。因其具有众多优势，固化流态底泥填方工程技术在国内外被广泛应用，应用时常选用水泥作为固化剂，并实施现场固化(节约大体量底泥的运输成本，降低运输过程中的环境风险[9])。典型案例有日本名古屋中部国际机场人工岛填筑工程[10]、新加坡Tekong岛围海垦地工程[11]、江苏省无锡市五里湖工程[12]。

目前，大量学者对固化流态底泥填方工程进行了相关研究，但研究中仍存在以下问题：(1)现场浇填的固化流态底泥施工速度快，一次性处理的底泥量体积庞大，难以搅拌充分，从而导致固化剂实际掺量的空间变异性；(2)流态底泥本身性能(矿物成分、含水率、颗粒级配等)的不均匀性；(3)现场养护条件(养护温度、养护压力等)的不确定性。这三方面的因素会导致固化流态底泥力学指标空间变异性往往比天然土体力学指标空间的变异性更为显著[13]，但目前文献中关于现场浇填的固化流态底泥剪切强度分布的空间变异特性的研究非常少见。相应地，关于现场固化流态底泥剪切强度的空间变异性对填筑体工程性能的影响程度和规律的研究还十分欠缺。

鉴于此，本文结合现场试验，探究固化流态底泥填筑体内剪切强度的空间变异特性，并结合理论分析方法，评价剪切强度空间变异性对固化流态底泥填筑路堤稳定性的影响程度和规律。

1 固化流态底泥剪切强度空间变异性现场试验研究

1.1 试验材料及设备

试验所用底泥为苏州常熟市白鹤滩±800 kV换流站工程内疏浚的荷塘底泥(以下简称为常熟底泥)，底泥的基本性质，粒度组成和颗粒级配曲线分别见表1和图1。根据GB/T 50145—2007《土的工程分类标准》，常熟底泥属于低液限黏土CL，固化剂选用标号为42.5的普通硅酸盐水泥和S95级矿渣粉(GGBS)。试验设备有HC-G-4.0型的混凝土/砂浆搅拌罐(罐体容量4.2 m3)、挖机等。

表1 试验用底泥基本物理性质指标

图1 试验底泥的粒径分布

1.2 现场试验方法

基于室内试验的研究结果，确定了最优的固化剂添加量，同时，为便于开展现场试验及添加相应材料用量，经过单位换算后，现场固化方案采用每m3流态底泥(含水率大致为170%～190%)添加水泥和GGBS各80 kg，分两层浇筑。

(1)使用挖机挖取一个倒梯形的试验槽(底部为2 m×2 m，垂直高度为2 m，坡率为1∶1.5)，成型后对底面进行人工平整(铲平表面并清除大块的泥样、杂质)，见图2a。

(2)使用挖机在HC-G-4.0型的混凝土/砂浆搅拌罐中添加流态底泥和固化剂，单次搅拌量为流态底泥3 m3(挖斗单勺容量约为1 m3，取3斗)，固化剂为水泥和GGBS各240 kg(用挖斗分别添加)，搅拌速率为10 r/min，搅拌时间为20 min。

(3)将搅拌完成的固化流态底泥从搅拌罐下部的出料口排出，并由挖斗将其缓慢、均匀地倒入试验槽中。本次现场试验分两层浇筑，以探究各层固化流态底泥剪切强度的空间变异性。浇筑完毕状态见图2b。

(4)在现场条件下养护至设定龄期后采用自行订制的无侧限抗压强度取样器进行分区块随机取样，并开展无侧限抗压强度试验。详见图3。

1.3 试验结果分析及讨论

养护一定龄期后对试验槽内固化流态底泥进行大规模取样和数据统计分析，结果见图 4，其中，层数的命名按浇筑的先后顺序进行；N为样本个数，μ为样本均值，σ为标准差，COV为变异系数。

从图4中无侧限抗压强度qu的统计结果来看，qu基本服从对数正态分布。对比图4中的样本均值μ可以发现，随着养护龄期的发展，两层固化流态底泥的qu均随之增大，且前期增长较快，后期增速有所减缓；在相同养护龄期下，第一层固化流态底泥的qu普遍高于第二层的qu，增幅为7%～12%不等，主要原因为养护压力的影响，第一层固化流态底泥在上覆层(第二层固化流态底泥)自重压力的作用下，土体孔隙中的自由水因挤压作用而逐渐排出，土颗粒与固化剂颗粒间的距离也随之拉近，水泥水化反应和火山灰反应生成的胶结产物[14,15]发挥的功效将更为显著。

图2 现场试验流程

图3 现场取样及室内试验

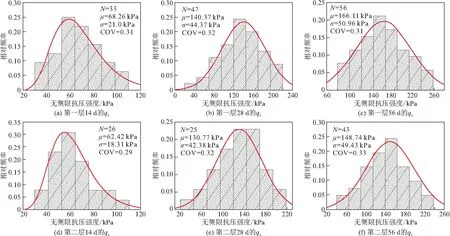
图4 无侧限抗压强度qu的相对频率统计及分布规律

由数据统计结果可以看出，第一层固化流态底泥的COV介于0.31～0.32，第二层的COV介于0.29～0.33，基本包含在Kasama等[16]总结的日本水泥土强度qu变异系数变化范围(0.30～0.99)内，可见水泥土的强度空间变异性较大。因此，当采用固化流态底泥用于填筑路堤等工程时，其强度空间变异性对路堤稳定性的影响值得关注。

2 强度空间变异性对固化流态底泥填筑路堤稳定性的影响

2.1 基于随机有限元理论的固化流态底泥填筑路堤稳定性分析

2.1.1 问题描述

所选填筑路堤模型的坡度为i=1∶1.1，填筑高度为10 m，底部宽33 m，顶部宽11 m。模型分为填筑路堤与地基两个部分，因本文只重点关注路堤堤身的稳定性，不关注路堤和地基的整体稳定性，因此将地基设为强地基，使破坏仅发生在路堤部分。采用Mohr-Coulomb模型，使用强度折减法进行计算，参考Lee等[17,18]的试验结果，取水泥土模量E与无侧限抗压强度qu的比值E/qu=135；黏聚力cu近似取为qu的1/2(不排水条件)。图1为该模型的断面图。

图5 模型断面/m

依据JTG D30—2004《公路路基设计规范》[19]，路堤稳定性计算分析得到的路堤堤身稳定安全系数不得小于1.35，本文通过经验估计与反复试算，最终确定了堤身稳定性安全系数为1.35时的模型各项参数。具体参数设置见表2。

表2 模型参数

2.1.2 不确定性分析

本文重点关注水泥土剪切强度(黏聚力部分)的空间变异性对填筑路堤堤身稳定性的影响，因此不考虑水泥土摩擦角和重度的变异性[20]，并将其他土性参数一同视为定值。无侧限抗压强度qu服从对数正态分布，均值取为40 kPa，其变异系数COV(qu)取为0.25，035，045，包含了前文0.29～0.33的统计范围。基于K-L(Karhunen-Loeve)分解法[21]对黏聚力随机场进行表征，采用蒙特卡罗法进行不确定性分析，每组工况实现次数为500次。随机场变量qu的分布规律为对数正态分布[22]，自相关函数为二次指数函数，相关距离取为1 m。所得堤身稳定性安全系数直方图与对数正态分布拟合结果如图6所示。

依据GT/B 50283—1999《公路工程结构可靠度设计统一标准》[23]相关规定，高速公路、一级公路和二级公路路堤稳定目标可靠度指标应控制在2.2～3.0之间。本文选择可靠度指标β=2.5进行分析，对应失效概率为0.621%。对各变异系数工况下所得的安全系数统计柱状图进行对数正态分布拟合，可得拟合曲线的均值、不同COV(qu)工况下所得安全系数的变异系数COV(k)和0.621%分位值(表3)。图7 为安全系数随变异系数变化曲线。

图6 不同变异系数工况下的稳定性安全系数统计结果

结合表3和图7可知，随着水泥土剪切强度变异系数COV(qu)的增大，安全系数的均值不断减小，不确定性分析的均值与确定性分析结果差值也越来越大。这意味着基于不确定分析结果的设计值与传统设计方法所得设计值的差距越来越大。从分布趋势和可靠度分析结果来看，COV(qu)越大，剪切强度变异性越强，安全系数计算结果的变异系数COV(k)越大，计算结果分散性越强，最高值与最低值差值越大。当变异系数COV(qu)=0.25时，可靠度指标β=2.5对应的k的0.621%分位值为1.157，当变异系数增大至0.45时，k的0.621%分位值仅有1.036，这意味着路堤已处于失稳边缘，必须在原有设计基础上进行加固。

表3 不同变异系数工况下计算结果

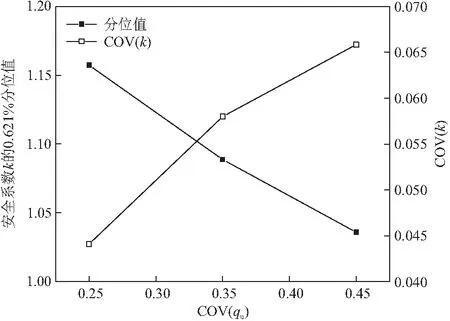
图7 安全系数随变异系数变化曲线

与确定性分析结果相比，不确定性分析所得结果并不满足规范中安全系数大于1.35的要求。这也意味着，水泥土剪切强度空间变异性的存在会使确定性分析高估水泥土填筑路堤堤身的稳定性。同时，从图6中可以明显看出，安全系数0.621%分位值随着变异系数的增大近似线性减小，这也表明传统设计方法会高估路堤堤身的稳定性，水泥土强度的变异性对路堤堤身稳定性安全系数的影响较为明显，在设计时应予以考虑。

2.2 固化流态底泥填筑路堤内土体抗剪强度设计值选取建议

目前在水泥土相关工程中，常假定水泥土的无侧限抗压强度qu服从正态分布，并选取25%分位值作为强度设计值qud。然而，由前文试验结果可知，对数正态分布对固化流态底泥无侧限抗压强度的拟合效果更优，因此常规水泥土设计方法中基于正态分布所提出的25%分位值未必能够有效地表征固化流态底泥剪切强度空间变异性对路堤堤身稳定性的影响。

选择可靠度指标β=2.5，通过2.1节不确定分析结果可知：无侧限抗压强度均值μ(qu)=40 kPa，COV(qu) =0.25，0.35，0.45工况下的路堤堤身稳定性安全系数的0.621%分位值分别为1.157，1.089，1.036。若通过确定性计算模型进行反分析，安全系数k为1.157，1.089，1.036对应的无侧限抗压强度分别为37.32，26.60，23.92 kPa。该强度可视为“与可靠度设计方法等效的确定性设计方法”的无侧限抗压强度设计值。因此，根据该强度设计值与无侧限抗压强度qu的对数正态分布曲线之间的对应关系，可确定出不同COV(qu)条件下固化流态底泥填筑路堤内土体抗剪强度设计值对应分位数的大小，见表4。

表4 不同COV(qu)条件下确定抗剪强度设计值的分位数建议值

由表4可知，在可靠度指标β=2.5的条件下，不同COV(qu)工况下，等效的确定性设计方法确定抗剪强度设计值的分位数建议值均远低于25%，因此，传统设计方法中，基于正态分布，按照经验所取的25%分位值并不适合对数正态分布的情况。除此之外，各工况下的各抗剪强度设计值分位数建议值随着变异系数COV(qu)的增大而逐渐增大，其增加速率也呈上升趋势，但整体增幅远低于与经验值的差距，变异系数COV(qu)对分位数建议值的影响是有限的,。

在变异系数COV(qu)=0.45的工况中，取变异系数COV(qu)=0.25时的分位值14.5% 对抗剪强度进行求解，所得结果为23.16 kPa，相较于16.3%分位值处的抗剪强度仅减小了0.76 kPa，减幅为3.2%；而在变异系数COV(qu)=0.35的工况中，14.5%分位值处的抗剪强度为26.24 kPa，相较于26.60 kPa仅减小了0.26 kPa，减幅小于1%。因此可以认为，在同一可靠度指标下，变异系数COV(qu)的强弱对分位数建议值的影响十分有限，可按照COV(qu)较低的工况统一取值。在本文所分析的工况与模型中，相应分位值可取为14.5%。

3 结 论

本文综合现场试验与数值模拟方法，探究了固化流态底泥填筑体内剪切强度的空间变异特性及其对固化流态底泥填筑路堤稳定性的影响规律。所得主要结论如下：

(1)现场浇填的固化流态底泥强度空间变异系数分布于0.29～0.33范围内；当采用固化流态底泥填筑路堤等工程时，应对其强度空间变异性进行考虑。

(2)传统的确定性设计方法会高估水泥土填筑路堤堤身的稳定性，水泥土剪切强度的空间变异性在必要时应予以考虑。

(3)传统设计方法基于正态分布选取的25%分位值并不适用于对数正态分布的情况，且会高估路堤内土体的抗剪强度，使得设计值选取偏大，从而降低路堤堤身稳定性，低估路堤失稳风险。