基于信息流交互的关键链项目缓冲区确定方法

吉格迪， 詹亚明

(内蒙古工业大学 经济管理学院， 内蒙古 呼和浩特 010051)

在日益激烈的市场竞争中，项目面临的复杂性和不确定性不断加剧，传统的项目进度管理方法(如计划评审技术、关键路径法)已不能满足现代项目管理的需要，如何使项目按时、高效完工成为项目管理者研究的重点。1997年Glodratt[1]首先将约束理论应用于项目管理并提出了关键链项目管理(Critical Chain Project Management，CCPM)方法。随着经济的高速发展，不同领域都更加强调工作效率、时间成本等因素，因而关键链项目管理方法被应用于更多领域，实践证明CCPM是一种强有力的项目调度工具[2～4]。目前对于关键链的研究，主要包括关键链的识别方法、缓冲区的设置等方面。关键链项目管理主要包含三种缓冲区：项目缓冲(Project Buffer，PB)、资源缓冲(Resource Buffer，RB)、接驳缓冲(Feeding Buffer，FB)。三种缓冲区在项目中的作用各不相同[5]。缓冲区的确定方法是关键链项目管理的一个重要部分，也是近些年研究的重点方向。其中以Glodratt于1997年提出的剪贴粘贴法(C&PM)[6]和Newbold于1998年提出的根方差法(RSEM)最为经典。在后续研究中发现，C&PM和RSEM均存在着缺陷。

为了克服C&PM和RSEM的不足，后续研究在考虑项目属性的同时提出了不同的改进方法计算项目缓冲区。Yang等[7]基于RSEM方法确定了影响缓冲的三个项目修正因子，并用数据进行模拟。Hu等[8]提出了一个改进的关键链项目管理的框架，在允许额外资源重新分配的基础下提出基于成本和进度稳定性标准的活动开始时间的计算方法。张俊光等[9]通过对项目计划进行分型调整，利用Logistics增长模型确定缓冲模型。张光军等[10]提出了一种风险导向下的多属性缓冲设置方法，该方法能够更好地处理不确定因素对项目进度的影响。胡晨等[11]提出了一种综合考虑资源影响系数、活动工期风险、非关键链剩余缓冲等影响因素的缓冲区确定方法。蒋红妍等[12]基于信息流交互传递对项目工期造成的影响，提出了基于信息和多资源约束的缓冲区计算方法。

实践证明，上述研究可以运用于不同环境下的缓冲区确定，并且能够提高项目的完工效率，降低项目成本。但也存在一定的局限性：(1)现有项目缓冲区计算方法在考虑资源紧张因素时往往只考虑了物质资源这一因素，很少考虑信息资源的约束，而信息资源频繁交互带来的返工风险会威胁到项目的按时完工。文献[12]虽然在计算缓冲区时考虑了信息流交互带来的返工风险，但却忽视了返工次数对项目参与者熟练程度和工作效率的影响。(2)对于项目涉及多资源条件下的缓冲区设置，现阶段研究大多考虑了物质资源数量的需求度，却忽视了资源的种类以及成本等因素在项目分配及使用过程中的受限程度。(3)在计算项目缓冲区时，以往研究较多采用三点估计法度量活动工期的风险，该方法在实际管理中具有较大的主观性，在计算缓冲区过程中存在主观性和不确定性。

鉴于上述局限性，研究提出一种综合考虑信息资源紧张度、成本物质资源紧张度、项目经理偏好程度等影响因素的关键链项目缓冲区确定方法，改进之处在于：(1)考虑到信息流交互传递(返工)对项目工期产生的影响，同时，考虑到返工次数对项目参与者熟练程度和工作效率的正相关性，研究通过引入DSM(Design Structure Matrix)理论以及学习曲线，提出活动返工安全时间的计算，并据此计算信息资源紧张度；(2)在衡量物质资源紧张度对活动工期的影响时，考虑到成本高的资源具有替代性差的特点，确定物质资源紧张度时将资源数量以及成本的约束考虑在内；(3)采用三角分布的逆累积函数法确定项目的安全时间，降低以往研究中对安全时间进行估算的主观性。

1 返工安全时间确定

1.1 信息流交互

Steward[13]在1981年指出，几乎所有项目活动之间都存在信息流，信息流能够体现活动之间内在的、真实的关系。信息流的传递方向可以分为两方面：一方面是上游活动向下游活动传递信息即顺序流动，另一方面是由下游活动向上游活动反馈信息也即逆向流动。在一组活动中信息流不断进行传递和反馈就形成了活动间的信息流交互。一个项目中信息流交互越频繁，表明项目在执行过程中的不确定性越大，发生返工的机率也越大。以活动间的耦合关系为例，A是B的上游活动，当活动A完工后会向活动B传递其初始信息，B在接受A的信息后会进行返工并将返工后的信息传递给A，这又会造成A的返工，如此往复，信息流的频繁交互导致的返工必然会对项目的工期造成影响。

按照信息流交互方式的不同，可以将活动分为重叠状态和非重叠状态。这两种状态下的活动都存在信息流的传递和反馈。非重叠状态下的信息流交互如图1所示，活动i是活动j的上游活动，图1a中阴影部分表示活动j完成时向活动i传递信息导致活动i发生返工的时间，即首次返工。图1b中的阴影2表示活动j完成后向活动i反馈信息导致活动i的返工完成时，活动i向活动j传递信息造成活动j的返工时间，即第二次返工。重叠状态下的信息流交互如图2所示，阴影1Tj表示当活动i开始向活动j传递信息时，活动j已经开始的时间，阴影2表示活动i向活动j传递信息以及活动j收到信息后向活动i反馈信息，如此往复直到活动i完成的时间。由图可知阴影1与阴影2的和表示活动i和活动j重叠的时间。上述分析可以发现：信息流的不断交互过程会导致活动j发生返工，因此活动j的返工安全时间即阴影3由阴影1和阴影2的函数来决定[14]。当不考虑信息流交互的情况时，估计的活动安全时间会比实际偏小。图中的阴影部分即考虑了信息流交互的作用。需要注意的是，本文对返工安全时间的计算不会使项目的持续时间变长，而是作为缓冲区来降低项目的不确定性。

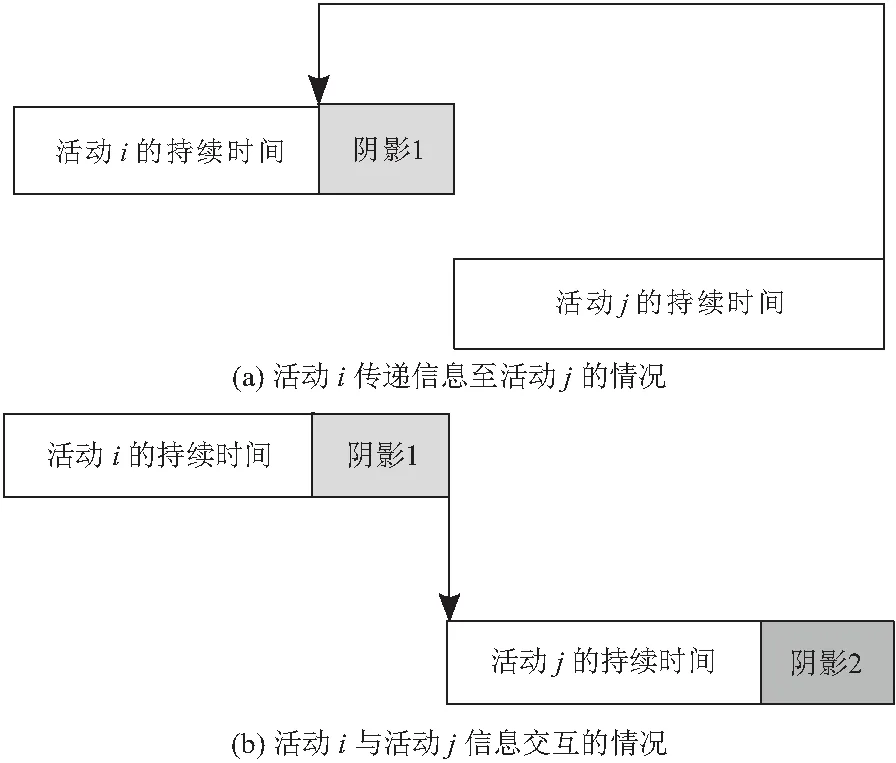
图1 非重叠状态下活动间的信息流交互

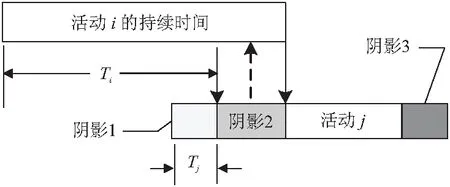
图2 重叠状态下活动间的信息流交互

1.2 基于DSM理论以及学习曲线确定返工安全时间

Steward于1981年提出使用设计结构矩阵法(DSM)来描述活动之间的迭代关系。在DSM矩阵中，其非对角线上的元素有数字或者“×”时，表示一个活动向另一个活动的信息流动的强度。当非对角线上的元素为0或者空格时，表示活动与活动之间不存在信息流动。对于DSM矩阵中的对角线上的元素，一般情况下没有意义，有时用对角线上的元素来表示活动的持续时间。

研究使用以下四个DSM矩阵来描述信息流交互的强度和概率[15]：信息输出时间因子矩阵O、信息输入时间因子矩阵I、返工概率矩阵RP和返工影响强度矩阵RI。以下是对上述四个矩阵的详细介绍：

如图3a所示的矩阵O为信息输出时间因子矩阵。非对角线上的元素O(i,j)表示活动j开始向活动i提供信息的时间，其取值范围为[0,1]。在图3a中，上对角元素O(2,3)=0.6表示当活动C完成其60%的活动时活动C向活动B反馈信息；下对角元素O(4,3)=0.7表示当活动C完成其70%时，活动C向活动D提供了信息。当矩阵中元素的数字为1时，如O(2,1)=1表示活动A完全完成后才向活动B输出信息。

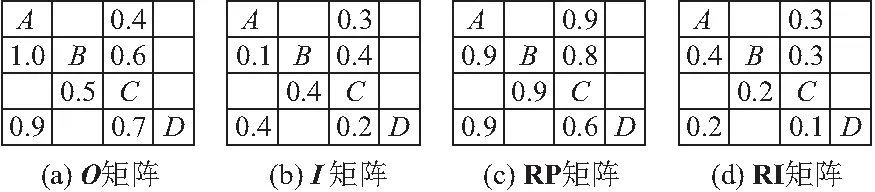
图3 DSM矩阵

如图3b所示为信息输入时间因素矩阵I。非对角线上的元素I(i,j)表示i开始从j接收到信息的时间，其取值范围为[0,1]。当I(i,j)=0时，表示活动i从一开始就接收活动j的信息。下三角中的I(3,2)=0.4表示当活动C完成了40%的工作时，活动C开始接收来自活动B的信息。上三角中的I(2,3)=0.4表示当活动B完成了40%的工作时，活动B开始收到活动C的反馈。

如图3c所示为返工概率矩阵RP。非对角元素RP(i,j)值表示活动返工的概率。其中，矩阵上三角形中的值表示由下游活动的信息反馈引起的上游活动返工概率，下三角中的值表示由上游活动信息传递引起的下游活动返工概率。前者表示首次返工的概率，后者表示第二次返工的概率。例如，RP(2,3)=0.6，表示活动C的信息反馈导致活动B返工的概率为60%。RP(3,2)=0.9表示活动B将信息传递给活动C后导致活动C返工的概率为90%。

如图3d为返工影响强度矩阵RI。RI(i,j)代表活动j造成活动i的返工时间占活动i持续时间的百分率。例如，RI(1,3)=0.3意味着活动C将信息反馈给活动A，导致活动A的返工时间占其总持续时间的30%。

大型建筑项目以及技术研发等项目中往往存在返工现象，一般情况下，随着工作重复次数的增加，项目参与者的熟练程度和工作效率必然会不断提升。如果在这些项目执行时忽视学习效应，往往会使项目进度计划比实际情况延后。如图4所示，箭头表示活动i和活动j存在着频繁的信息交互，即存在返工风险，图4a表示不考虑学习曲线LCi的作用时，项目管理者估计的返工安全时间。图4b表示考虑学习曲线时，得到的预计返工安全时间。当项目存在返工风险时，对于具有同质的项目活动而言，多次返工会促使学习效率提高，提高返工安全时间计算的准确性，进而提高缓冲区计算的准确性。因此学习曲线在计算返工安全时间时至关重要。

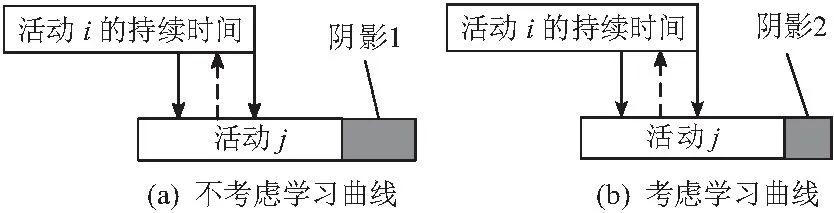
图4 返工安全时间对比

由文献[15]可知，返工风险是返工概率和返工影响强度的函数。由于在返工过程中参与者可能会受益于学习和适应程度的提高，而使原来计算的返工时间偏大，因此本文引入学习曲线LCi来提高计算返工安全时间的准确性[16]。上述提出的矩阵中元素的值可以从历史数据中收集，也可以根据项目团队的风险偏好进行估计。设RSTi表示活动i的返工安全时间,di表示活动i的持续时间。

图1中阴影1，2所表示的预期返工时间可用式(1)表示。

RSTi=RP(i,j)RI(i,j)diLCi

(1)

图2中，阴影3所表示的返工安全时间可用式(2)表示。

RSTi=(S1+S2)RI(i,j)RP(i,j)LCi

(2)

S1+S2=di-Ti+Tj

=O(i,j)di+(1-I(i,j))dj

(3)

式中：S1为图2中阴影1的面积；S2为图2中阴影2的面积；di，dj分别为活动i，j的持续时间。

2 项目缓冲区的确定

2.1 信息资源紧张系数

由于信息资源的可得性是有限的，有些信息资源只能在活动的实施过程中产生，因此不会出现信息资源供过于求的问题。由上述分析可知：信息资源的可使用量包括项目持续时间以及返工安全时间，信息资源在一定时间内的供应量仅仅包括项目持续时间。因此，参照文献[14]用信息资源使用量与信息资源供应量的比值来确定信息资源紧张系数。若用αi表示信息资源紧张系数，则其表达式为：

(4)

2.2 成本物质资源紧张系数

在关键链项目管理中，物质资源通常指机器设备、原材料、资金等[17]。以往研究在确定物质资源紧张度时通常分为两种情况，一种情况是考虑单一资源的紧张度，另一种情况是考虑多资源紧张度。一些学者采用资源使用量和相应时间段内资源可用量的比值来计算单一资源的物质资源紧张度βi，如式(5)所示。

(5)

式中：ri为活动i所需资源的数量；T为使用该资源的活动总时间；R为该资源的可用量。朱建信[18]采用平均值法来求多资源的资源紧张度，如式(6)所示。

(6)

式中：R(a)为活动i中资源a的使用量；Rs(a)为资源a的总供应量；n为活动i所使用资源的种类；k为活动i在执行时间内使用资源a的数量。

上述方法在计算物质资源紧张度时，没有考虑到不同资源之间的成本差异，而资源的类型以及成本在项目进度计划中起着至关重要的作用。因此，本文提出改进的物质资源紧张系数的概念，该系数将不同资源统一采用成本信息度量。设βi表示物质资源紧张系数，RCa表示资源a的成本，na表示一定时间内资源a的使用量，Na表示资源a的总供应量，则在一定的时间内，基于成本的物质资源紧张系数可以用项目使用的资源成本与项目总成本的比值表示，如式(7)所示。

(7)

本文提出的物质资源紧张系数的计算方法不仅能够体现对资源数量的约束，还可以体现资源成本的约束，对企业在选取资源的时候具有一定的参考价值。

2.3 项目经理风险偏好

项目管理者对于项目的价值评估以及对风险的主观认知等方面有很大的差异，会选择不同的项目按期完成保证率，因此项目经理的偏好程度也会对项目工期产生影响[19]。理想状态下，当活动中包含的活动较多时，根据中心极限定理，整个活动近似的服从正态分布。记项目经理风险偏好水平为ε，通过查正态分布表可知，在1-ε保证率下对应的标准差倍数为f1-ε。可以计算项目经理风险偏好调整系数λi为：

(8)

当ε=5%时，即该项目有5%的可能性使缓冲超出控制范围，也就是说项目经理将在95%的保证率下设置项目缓冲。本文假设项目经理的风险偏好水平为5%，意味着项目需要在95%的保证率水平下完工，查表可知95%保证率对应的标准差倍数为f1-ε=1.65，由式(8)可知，项目经理风险偏好调整系数λ=0.875。

2.4 项目缓冲区的确定

2.4.1 基于三角概率分布确定活动安全时间的度量方法

根方差法通常采用活动方差来表示活动i的安全时间σi，σi=ρi-di，其中ρi表示活动i在安全时间内完成的工期，di表示活动i最可能完成的时间。本文在已知各个活动持续时间的最乐观值、最可能值、最悲观值的情况下，根据活动的三角概率分布的逆函数法(逆累积分布函数法)，采用MATLAB软件进行蒙特卡洛模拟仿真各个活动的随机工期，设置随机数的个数N=500，将各个活动的随机工期在置信度95%和置信度50%时分别对应的工期估计值T95%，T50%定义为该活动的安全完成时间以及可能完成时间[6]。则活动安全时间可由式(9)表示。

σi=T95%-T50%

(9)

2.4.2 确定项目缓冲区

研究综合考虑了信息资源紧张度αi、成本物质资源紧张系数度βi、项目经理风险偏好λi以及基于三角概率分布确定的活动安全时间σi等因素对项目不确定性的影响，提出了项目缓冲区PB的计算公式，如式(10)所示。

(10)

3 算例分析

3.1 算例介绍

选取文献[20]中的算例进行分析，该算例是由20个活动组成的项目。由于本研究致力于计算项目缓冲区，因此只需考虑关键链上的活动，而不用考虑非关键链上的活动。由文献[20]可知，优化后的关键链为A→B→D→G→J→M→N→O→P→R→S。关键链上活动的基本信息如表1所示。关键链中的各活动间信息流输出矩阵(O矩阵)、输入矩阵(I矩阵)、返工概率矩阵(RP矩阵)以及返工影响强度矩阵(RI矩阵)如图5所示。假设关键链上活动所需的资源a，b，c的单价分别为500，200，700, 单次使用资源数量的上限分别是4，6，2。

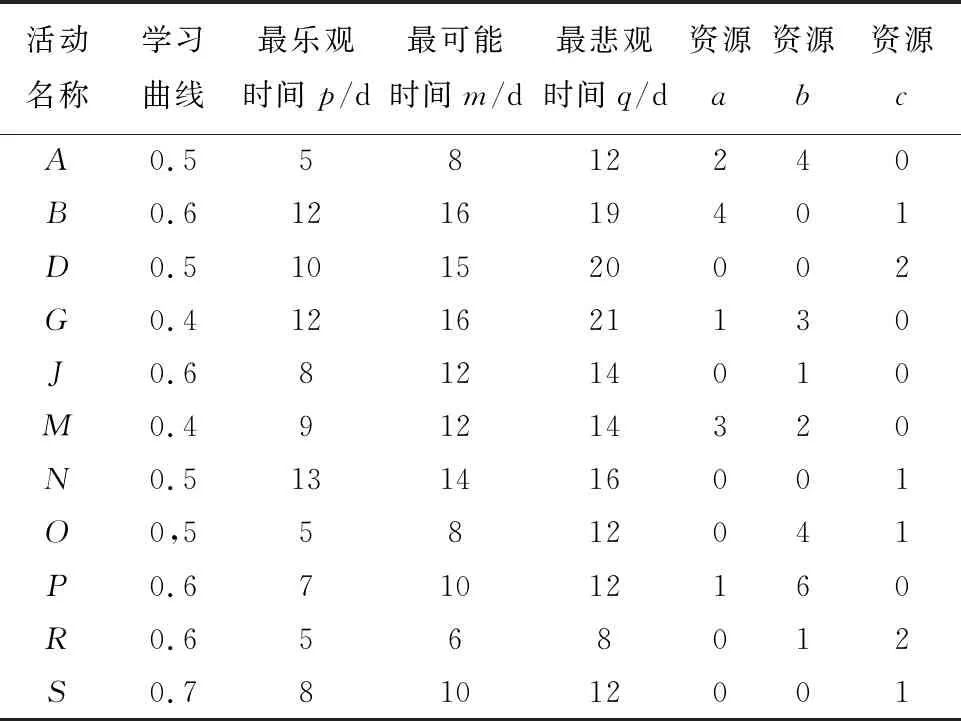
表1 案例中相关活动参数

3.2 项目缓冲区的确定

3.2.1 计算信息资源系数

首先，根据式(1)～(3)以及图5中的详细信息，运用MATLAB进行编程，计算出关键链上活动的返工安全时间，然后根据式(4)计算各个活动的信息资源紧张系数，计算结果列于表2第7列。

图5 DSM矩阵

3.2.2 计算成本物质资源紧张系数

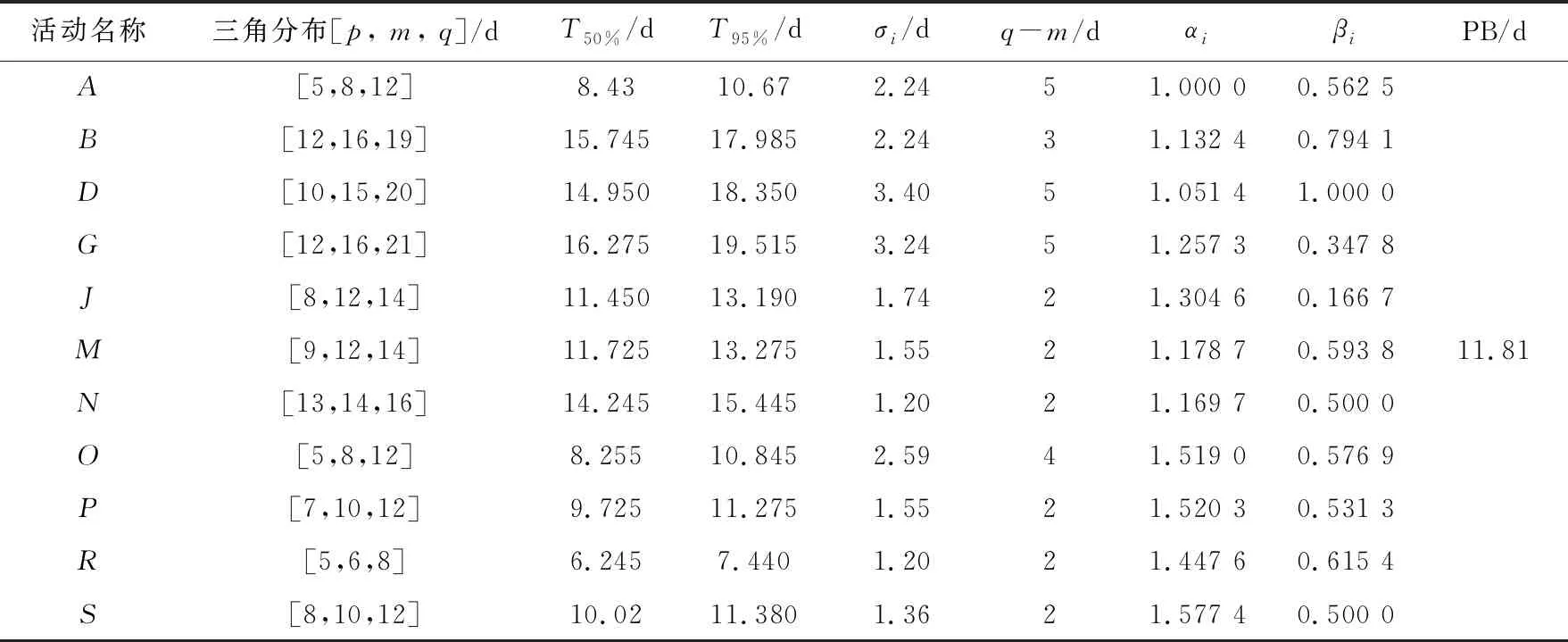
表2 项目缓冲区参数计算

3.2.3 计算活动安全时间

为了克服以往研究在确定计划工期和安全时间过程中采用三点估计法的主观性，研究根据活动的工期分布利用MATLAB软件对活动工期进行蒙特卡洛模拟。根据三角分布的逆函数法即逆累积分布函数，设置随机数N=500，统计区间数量K=50，模拟出关键链上各活动的随机工期。以活动A为例，图6为利用MATLAB软件生成的活动A的随机工期分布直方图。基于仿真结果，可得到T95%=10.67，T50%=8.43，活动安全时间为2.24 d。仍然以活动A为例，根据活动工期服从的三角分布的最可能值和最悲观值所确定的活动安全时间为4 d。通过两种方法的对比可知，在保证客观性的情况下本文得到的安全时间明显缩短。根据模拟的活动随机工期分布图计算出各个活动置信度T95%值、置信度T50%值和活动安全时间σi的值，如表2第3～5列所示。

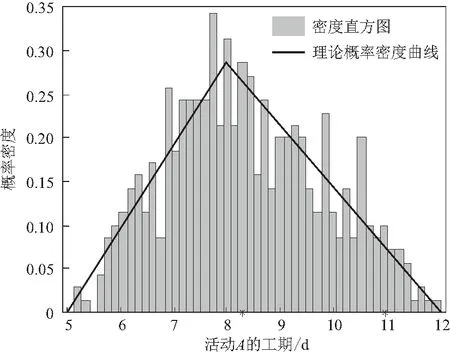
图6 活动A的随机工期分布

3.2.4 计算项目缓冲区以及项目计划总工期

根据上述信息计算出项目缓冲区所需参数，然后通过式(10)计算项目缓冲区。研究采用尾部集中法计算项目缓冲区，将关键链上各个活动计算出的项目缓冲区加起来得出最终关键链上的项目缓冲区。项目持续时间取决于关键链上各个活动的持续时间，因此，研究选取每项活动的随机工期模拟数据均值作为活动的计划持续时间，项目计划总工期等于关键链上各个活动的计划持续时间以及所计算的项目缓冲区之和。仿真结果表示：该项目的缓冲区为11.81 d，计划持续时间为125.2 d，计划总工期为137.01 d。

3.3 几种算法的比较分析

采用MATLAB软件进行仿真，将仿真结果运行500 次，得到剪贴粘贴法(C&PM)、根方差法(RSEM)以及本文方法(CCDSM)的项目缓冲区、实际持续时间以及项目工期频数分布图及累计概率密度的对比图，如图7，8所示。

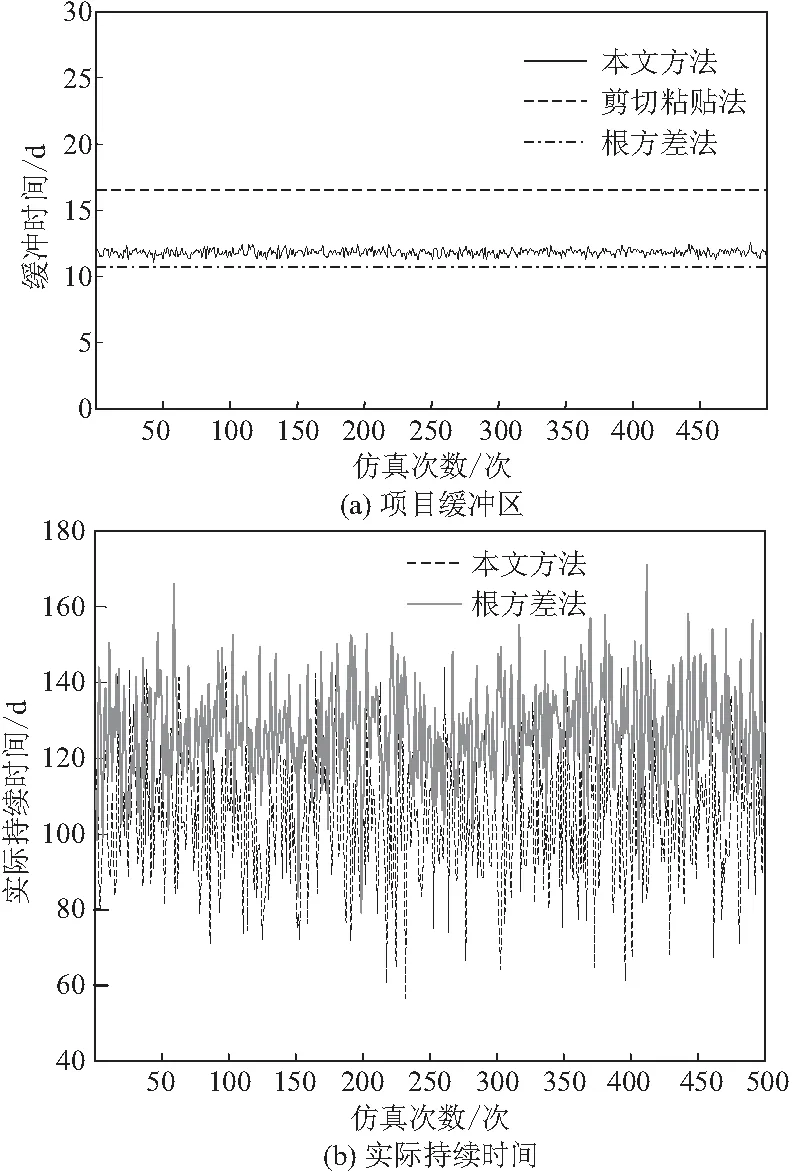
图7 不同方法的项目缓冲区和持续时间的对比

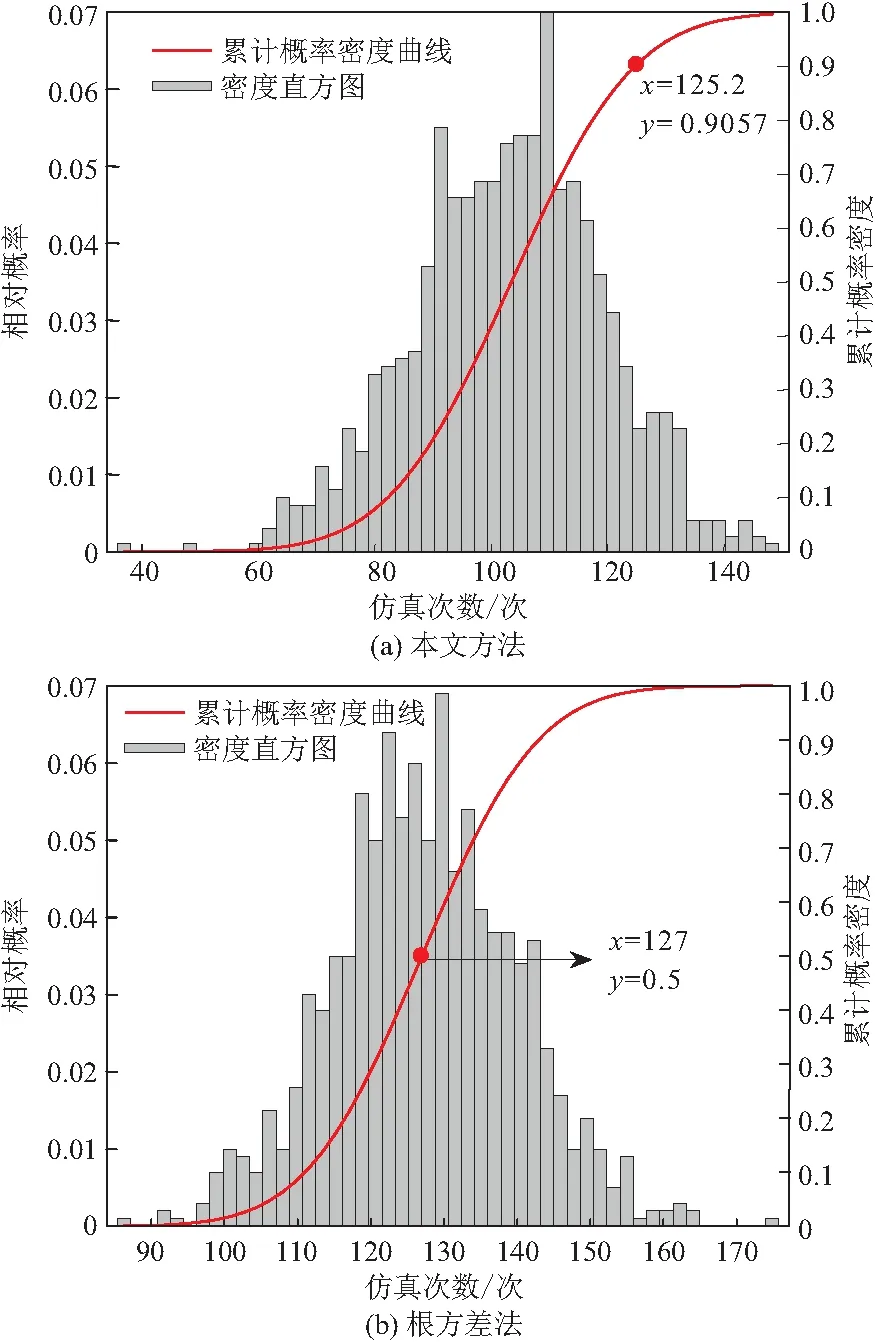
图8 项目工期频数分布图及累计概率密度对比

如图7a所示，本文提出的方法(CCDSM)计算出的项目缓冲区小于C&PM大于RSEM。 首先，CCDSM计算的项目缓冲区小于C&PM，这是由于C&PM 计算的缓冲区将项目安全时间的四分之一作为项目缓冲区，也即C&PM 随着活动个数的增多所得到的缓冲区值成线性增加的态势，当项目较多时必然会因为缓冲区过大而造成过度保护。其次，CCDSM 计算的项目缓冲区大于RSEM，这是由于RSEM 假设活动间是相互独立的并采用各个活动安全时间一半的平方和的平方根来计算项目缓冲区，而CCDSM 确定项目缓冲区的方法不仅考虑了项目准备阶段的不确定性，而且考虑了项目进行过程中的不确定性即信息流导致的返工风险。由上述分析可知，CCDSM计算的项目缓冲区优于RSEM以及C&PM。同时，本文从统计学的角度计算项目安全时间，由此计算出的缓冲区能够减少项目估算过程的不确定性，因此更加合理。

由图7b可知，本文所提方法模拟的项目实际持续时间比RSEM模拟的项目实际持续时间更短，且由图8可知，RSEM方法模拟的项目平均计划工期为127 d，其对应的完工率为50%，本文方法模拟的项目平均计划工期为125.2 d，其对应的完工率为90.57%，远大于RSEM的50%。这是由于本文所提方法考虑了信息流交互对项目进度计划的影响，尤其是信息反馈对项目工期的影响(从图5中能够看出，在DSM矩阵中，上三角形中的点数比下三角形的点数少很多，这表明反馈点的数量已经减少到最小值)。由上述分析可知，项目管理者在实际管理中，不仅要考虑传统资源(如人力资源、物质资源、财政资源)对活动工期进度计划的影响，还要注意信息流频繁交互对项目工期产生的影响。管理者可以通过减少信息反馈次数来缩短项目实际持续时间(项目工期)，提升项目按时完工率，降低因信息流交互频繁带来的额外通信成本，促使项目按期高质量完工。

4 结 论

在日益激烈的市场竞争中，项目面临的复杂性和不确定性增大，如何使项目按时、高效完工成为项目管理者研究的重点。考虑到项目资源(信息资源、物质资源、管理者偏好)对项目进度产生的重要影响，研究提出一种综合考虑信息资源紧张度、物质资源紧张度、项目经理偏好程度等影响因素的关键链项目缓冲区确定方法。通过引入DSM理论以及学习曲线来量化信息流交互带来的返工风险，据此计算信息资源紧张系数；在衡量物质资源冲突对活动工期的影响时，考虑了资源数量和成本的双重约束。这不仅提升了缓冲区的准确度，也使缓冲区设置更符合项目实际情况。通过仿真分析，得出以下结论：(1)在项目存在返工风险的情况下，研究所提出的缓冲区计算方法在克服了C&PM和RSEM不足的情况下，能够降低信息资源冲突对项目进度的影响；(2)项目管理者在对项目进行实际管理时，不仅要注意物质资源以及人力资源冲突对项目进度的约束，还要注意信息流交互带来的返工风险对项目进度的影响；(3)项目管理者可以根据项目进展情况，及时加强对组织结构的调整，减少活动间信息流交互次数，这将有助于缩短项目工期、提高项目按时完工率、降低因信息流交互频繁带来额外的通信成本。