电流互感器饱和检测以及畸变电流补偿

胡红利，崔晨辉,员鹏宇,2,段羽洁,张 肖

(1.西安交通大学 电力设备电气绝缘国家重点实验室,陕西 西安 710049;2.国网合肥供电公司,安徽 合肥 230022;3.西安市产品质量监督检验院,陕西 西安 710065)

电流互感器是电力系统中的重要设备,在传输电能以及动力系统中都具有不可替代的地位[1]。在正常运行情况下,电流互感器的铁心工作在线性区中,此时，由于励磁阻抗非常大,励磁电流非常小,一次侧的电流几乎没有损耗地转化到二次侧电流上,传输特性很好。但是，由于如直流偏磁、谐波或者接地短路故障的发生,使得电流互感器进入饱和区,二次侧电流发生畸变，导致继电保护装置误动作[2]。因此，对于运行中的电流互感器的饱和检测以及畸变电流补偿至关重要。

对于饱和检测的研究,Kang等人提出利用差分法检测饱和,在未饱和区域,二次侧电流的二阶、三阶差分输出的值很小,小于提前设置的限值,而在进出饱和点,二阶、三阶差分输出明显超过限值[3]。但该方法也存在一定的缺陷,二次侧是否饱和的判断会直接受到提前设置限值的影响,对于那些轻度饱和的电流互感器,差分法检测准确率较低。袁金晶等人指出电流互感器饱和时,二次侧检测到的谐波等效于基波电流叠加谐波电流,高频谐波含量决定二次侧电流饱和严重程度[4]。因此，计算谐波与基波的比例即可判断有无发生饱和以及饱和程度。

对于电流补偿的研究,Pan等人认为由于电流互感器出现饱和以及误差的根本原因在于励磁电流,所以，只要计算出励磁电流以及因为励磁电流而导致的二次侧偏差,再将畸变的二次侧电流加上这个偏差,即可得到接近于理论输出的二次侧电流[5]。但是该方法没有将铁心中存在的剩磁对二次电流的影响考虑在内,使得该方法目前还没有普遍使用。Cataliotti等人将一次电流进行泰勒公式展开,将没有发生饱和的二次电流进行线性回归,即可补偿已经发生饱和畸变的二次电流。该方法原理简单、计算量小,但该方法高度依赖饱和识别算法,饱和区间能否准确识别是该方法的前提[6-7]。

本文在PSCAD中仿真接地短路后电流互感器二次侧波形,并采集波形数据。将波形数据导入至Matlab中，使用小波变换检测饱和以及使用RBF神经网络将已经畸变的二次侧电流补偿成未畸变的期望值。

1 电流互感器暂态饱和仿真分析

本文在PSCAD中搭建仿真电路，模拟电力系统中单相接地短路故障,从而导致电流互感器发生暂态饱和。采用双端输电线路设计,电源选择集中参数模型[8-9],两端发电机的额定容量为100 MV·A,电源阻抗设置为(1.200+j6.648)Ω,额定电压为220 kV,额定频率为50 Hz，线路总长度为300 km。本次仿真系统的采样率设置为2 kHz,即每个周期40个采样点。搭建的仿真电路如图1所示。

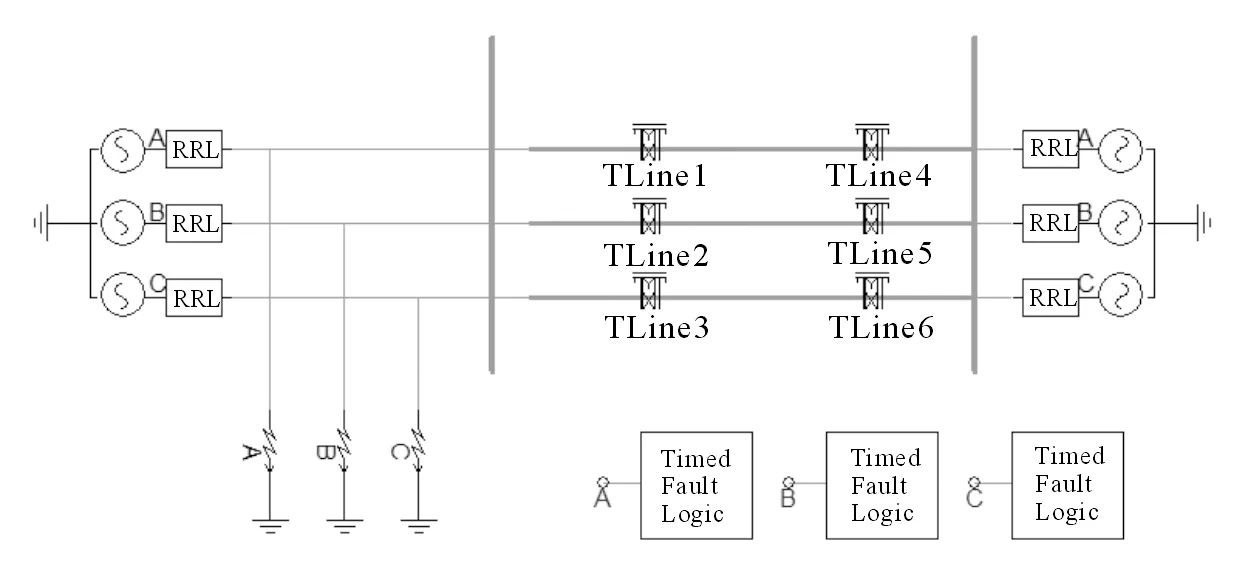
图1 饱和特性仿真电路Fig.1 Saturation characteristic simulation circuit

本次实验电流互感器匝数比为5/500,负载为2 Ω,无剩磁,本次接地短路为A相的区外故障,接下来改变电源额定电压分别为110 kV、220 kV和330 kV,从而可以对接地短路后的母线电流进行调整,仿真结果如图2所示。

黑色曲线为一次侧电流按照电流变比折算到二次侧的波形,红色曲线为仿真后的畸变二次测波形。在0.7 s时发生单独的A相接地短路故障,整个接地故障持续0.3 s,之后一次侧回路即恢复故障前的运行状态。由图2可知,随着额定电压从110 kV增至330 kV时,二次侧电流的幅值越来越大,并且波形发生畸变的时间越来越提前,波形发生畸变的程度越来越深,持续时间更长,饱和越来越严重。这是由于当一次侧额定电压越大时,发生短路之后,短路电流也会越大,使得铁心中增加的磁通也越多,铁心更容易饱和。

图2 在单相接地故障时不同额定电压对应的饱和电流波形Fig.2 Saturated current waveform with different rated voltage in case of single-phase grounding fault

2 基于小波变换的饱和检测

电力系统通过电流互感器检测电流，发生故障时,故障电流可能导致电流互感器饱和并产生测量误差,进而引起电流差动保护系统的误动，为了防止误动，电流互感器要进行饱和检测[10]。由于电流互感器在饱和时,其二次侧的电流会因为饱和而畸变,并伴随着二次侧电流中含有大量谐波,因此，可以通过检测谐波的手段来实时检测其铁心有无出现饱和的情况。

针对检测波形信号的谐波,傅里叶变换是目前最常使用的方法之一,对于任何一个波形信号f(t),如果式(1)成立,那么可以对其进行傅里叶变换,如式(2)所示。

(1)

(2)

但是，傅里叶变换是在频域上进行计算分析,因此，其只能得出在某一段时域信号中含有哪些频率的谐波以及含量比例,无法具体确定这些谐波信号各自出现的时间以及持续的时间[11],给实际使用带来了不便。

对于傅里叶变换的局限性,小波变换作为其进一步的发展[12]。在小波基宽度不变的情况下,对于时域原始信号不同频率幅值的部分,将选中的小波基通过收缩以及平移的方式对原始信号进行“扫描”,原始信号频率低的部分则将小波基的频率降低,频率高的部分将小波基的频率提高,以便匹配不同的高低频信号[13-14]。

设时域上的函数Ψ(t)平方可积,Ψ′(ω)为其傅里叶变换,如果满足式(3),则Ψ(t)是一个基本小波，

(3)

则连续小波函数可以定义为

(4)

其中：a为小波函数的尺度,用于控制其伸缩,以便匹配不同的频率段;τ为小波函数的平移量。

为了验证当电力系统中出现故障时,运用小波变换可以准确识别故障发生和结束的时间以及二次侧电流畸变严重程度。将图2的畸变二次侧电流波形数据从PSCAD中导出,并使用fopen函数导入到Matlab中,选取cmor为小波基,对图2的畸变二次侧电流波形数据使用连续小波变换，以检测饱和发生以及持续时长,其时频图如图3所示。

在图3中,时频图的颜色标尺深浅所代表的值为连续小波变换后的系数矩阵值,并且系数矩阵值与电流的幅值表现为正相关,即在时频图中颜色标尺数值越大的地方,此处对应频率的电流幅值就越大。由图3A可知,当电力系统中没有短路故障发生时,经过小波变换后的二次侧电流的时频图在2 s内检测为50 Hz,此时没有高次谐波干扰,二次侧电流没有发生畸变。由图3B可知,当线路中发生了单相接地短路故障并且电源额定电压为110 kV时,由于设置的故障发生时间在0.7 s,持续时间为0.3 s,从时频图中可以看出,小波变换可以及时并且精确地识别检测出电流互感器的饱和区间。由图3C和3D可知,随着故障时电源额定电压的提高,使得一次侧电流也跟随提高,导致电流互感器饱和和二次侧电流畸变的程度更加严重,并含有了次数更高的谐波,这时通过小波变换的时频图仍然可以精确地检测出二次侧畸变电流所包含的各次谐波。小波对各类噪声以及微弱信号也很敏感,在实际信号处理中,应设计小波滤波器先对信号进行滤波处理[15]。

3 基于RBF神经网络的电流补偿

径向基函数(radial basis function，RBF)神经网络作为前馈型神经网络的一种,可以很好地实现非线性映射,其结构也是分为3个层次,分别为输入层、隐含层和输出层[16]。其中，每一层都有着各自的功能,输入层用来接收外界输入数据,并把数据传输给下一层隐含层,n为外界输入数据的维数。隐含层具有m个神经元,其激励函数为径向基函数,隐含层神经元的个数可以根据具体情况进行选择,避免了局部极小值等问题,其中，隐含层第i个神经元的输出如式(5)所示[17-18]，

(5)

其中:X为n维输入向量;ci为隐藏层第i个神经元径向基函数的中心;q为分布密度。

在RBF神经网络中,通常用高斯函数作为基函数,用于调节神经元的敏感程度，使得神经网络运算能力得到很大提升[19]。

输出层第j个神经元的输出如式(6)所示，

(6)

其中：Wij为输出层权值；x为网络输入，φi(x)为隐藏层的输出。

RBF神经网络的结构如图4所示。RBF神经网络具有强大的非线性拟合功能,本文将接地短路故障发生后畸变的饱和二次侧电流采集值作为RBF神经网络的输入,将理论上无畸变的二次侧电流作为输出,训练神经网络。之后，将不同工况下得到的饱和二次侧电流数据作为RBF神经网络测试集,将由测试集得出的输出值与理论值做对比并计算误差。

本次仿真所收集的二次侧畸变电流训练数据样本为以下3种工况所组成的27组数据:故障初始角分别为0°、45°和90°;铁心剩磁分别为-2T、0T和2T;故障点位置距离左侧母线分别为10 km、30 km和60 km。

图4 径向基函数神经网络结构Fig.4 Neural network structure of the radial basis function

接下来引入类似电流互感器比差的定义[20],以衡量RBF神经网络补偿效果,如式(7)所示，

(7)

其中:It为理论电流的有效值;Ic为补偿电流的有效值。

经过上述训练集数据训练的RBF神经网络,为了测试其对于新的数据组能否有良好的逼近效果,以便在实际电力系统当中使用,本文分别采取以下3种工况设置来探究RBF神经网络用于电流补偿的效果。

1) 故障发生处距离左侧母线20 km、故障初始角为30°、铁心剩磁为1 T，仿真补偿结果如图5所示。其中：蓝色曲线为已经由于铁心饱和而畸变的实际二次侧电流；黑色曲线为理论上的二次侧电流；红色曲线为经过RBF神经网络补偿后的二次侧电流。由图5可知，在接地短路故障刚开始发生时的大概4个周期,由于畸变程度严重,使得个别数据点拟合补偿效果不理想,但在0.7～1 s的故障时间中,整体的电流补偿效果很好。为了更加精确地衡量该次RBF神经网络的补偿效果,使用式(7)的标准,该次补偿的精度为0.45%,说明基于RBF神经网络的算法可以很好地实现畸变电流补偿。

图5 实例1的电流补偿结果Fig.5 Current compensation result of example 1

2) 故障发生处距离左侧母线20 km、故障初始角为60°、铁心剩磁为1 T，仿真补偿结果如图6所示。由图6可知,当故障初始角为60°时,在第一象限内随着故障初始角的增大,故障发生瞬间的直流分量会越小。因此，对电流互感器铁心饱和的影响程度更小,二次侧电流的畸变程度更小,所以，此次仿真在开始的几个周期也可以取得很好的补偿效果,同样由式(7)可以得出该次补偿的精度为0.15%。

图6 实例2的电流补偿结果Fig.6 Current compensation result of example 2

3) 故障发生处距离左侧母线50 km、故障初始角为180°、铁心剩磁设置为-1 T，仿真补偿结果如图7所示。由图7可知,当故障初始角为180°时,使得初始直流分量为负值,从而电流互感器进入反向饱和,同样由式(7)可以得出，该次补偿的精度为0.48%。因此可以看出,当首先选取不同工况下得出的训练集训练RBF神经网络后,该神经网络已经具有良好的泛化能力,在其他工况下,也可以很好地补偿二次侧畸变电流。

图7 实例3的电流补偿结果Fig.7 Current compensation result of example 3

4 结语

本文在分析输电线路单相瞬间接地故障时产生电流互感器二次侧畸变电流处理方法的基础上,搭建了暂态饱和仿真电路,得到了不同工况下的饱和数据；并使用小波变换检测二次侧波形是否饱和。仿真结果表明,小波变换可以准确识别饱和开始、结束时间以及饱和严重程度。最后，将饱和的二次侧电流数据通过RBF神经网络进行补偿,经过该神经网络训练后,能正确补偿二次侧畸变电流,补偿后与理论上的二次侧电流接近,误差普遍在0.5%以下。