Matlab数字图像处理与矩阵概念及运算教学的融合

2022-02-25周克娟

广西广播电视大学学报 2022年5期

周克娟

（常州开放大学理工学院，江苏常州 213000）

一、引言

矩阵（Matrix）的概念及运算规律是由英国数学家阿瑟·凯利和詹姆斯·约瑟夫·西尔维斯特于19世纪50年代提出的，最早来自于方程组的系数及常数所构成的方阵。“矩阵”是线性代数初步的内容，它是在系统学习了行列式的定义、性质基础上，进一步研究矩阵理论，并在后续线性方程组求解的课程中发挥着重要的作用，因此掌握好矩阵的学习对工科数学课程的学习有重要意义。

随着计算机技术的快速发展，计算机辅助课堂教学亦得到广泛的应用，计算机的发展助力了数学软件的深入研发，这为数学课程的教学拓宽了思路。矩阵的相关理论及其算法在数字图像的分析和处理中应用广泛，如指纹自动识别技术、人脸自动识别技术、车牌识别系统中图像的读取、图像预处理、边缘检测、车牌定位等功能的实现。考虑到矩阵的概念及其运算的教学内容极具抽象性，传统讲练结合的教学方式不能生动地呈现出教学内容，难以激发学生的学习兴趣。在工科专业的矩阵的概念及其运算的教学过程中，潜移默化地加强思想政治教育，并与数字图像处理的相关实验相融合[1]，借助于数学软件Matlab将矩阵的知识加以拓展和可视化[2]。引导学生注重理论和实践相结合。突出跨学科整合科学、技术和工程、数学等核心特征，符合以产出（学习成果）为目标导向，以学生为主体地位的OBE（Outcome basededucation）教育理念。

二、运用Matlab软件进行矩阵可视化教学的实践

当前，大学生通过使用美图秀秀、醒图、黄油相机等手机修图软件处理图片并发布到社交软件、媒体平台，可见学生接受这种具体化、形象化的方式，而矩阵的概念以及运算这部分的知识较为抽象，难以充分调动学生学习的积极性。因此，本文对这部分的教学设计进行探索与实践，引入图像处理实例来可视化矩阵的相关知识，将抽象的理论知识变得更直观形象。

Matlab（matrix&laboratory）即矩阵实验室，软件一经研发就在众多领域应用，是进行数据分析、图像处理、信号处理的三大数学软件之一，其强大的图形处理系统能够快捷地图形化显示矩阵，并自带了二维三维图形函数、图像处理和动画显示等函数。它可以实现给图像添加滤镜效果，如浮雕、怀旧色、连环画、羽化、素描、强光等，还可以实现图像拼接、图像融合、图像分割、校正等功能[3][4]。本研究基于Matlab数字图像处理的矩阵的概念及其加法、减法、数乘、乘法基本运算的教学应用。

为提高课堂教学实效，突出“以教师为主导，以学生为主体”的教学理念，基于“课前——课中——课后”一体化教学模式设计教学环节。课前，教师线上发布课件、Matlab编程的主要代码等教学资源，发挥混合式课堂的教学优势；课中，教师讲授理论知识并演示对应的Matlab图像处理可视化操作程序，引导学生实践操作；课后，教师布置研究型的任务供学生挑战与探索。三个环节环环相扣，层层递进，使得学生课前有抓手、课中有目标、课后有任务，在提高学生自主学习能力的同时加深对重难点知识的理解与实际运用。

（一）从数字图像的角度引入矩阵的概念

从现实中获取数字图像的方法很多，如数码相机、扫描仪、CT或者磁共振成像。在课堂实际教学过程中，教师在介绍数字图像时可以导入图画，使用Photoshop等图像编辑器打开图像，当用放大镜放大查看时，还可以看到很多的小方格。这每一个方格代表的就是图像的一个像素，所谓像素是整个图像中不可分割的元素。一张图像是由像素点排列成正方形或者长方形。事实上，数字图像的数据可以用矩阵的形式来表示，一张尺寸为16×16的二值图像就对应一个16×16的矩阵，矩阵的行对应图像的高（单位为像素），矩阵的列对应图像的宽（单位为像素），矩阵的每个元素值对应图像的每个像素值，所以对数字图像的处理实际上就是通过操控矩阵来实现的。

在Matlab中调用“A=imread（filename）”函数读取灰度图像的数据后保存的数据是uint8类型，也就是每一个像素值都是由0～255之间的数字量化的，这256个数字衡量着图像灰度的深浅，值越大，代表越亮，值越小，代表越灰，0代表黑色，255代表白色。而将uint8类型转换为double类型后像素值的范围变成了0～1之间，也就是说0代表黑色，1代表白色，中间各数值则代表不同的灰度等级状态。

在掌握了矩阵的概念后学生还要了解零矩阵、单位矩阵、对角矩阵、上（下）三角矩阵的定义。在Matlab中调用显示图像函数“imshow（A）”将抽象的概念形象化、可视化，触发学生的联想和想象的能力，让学生轻松、高效地学习和理解概念。从二值图像（黑白图像）的角度解读特殊矩阵，如图1所示，调用“zeros（m，n）”函数构造了三个不同阶数的零矩阵，这三个零矩阵可视化图像显然不同，这表明不同阶数的零矩阵是不相等的。如图2所示，利用“eye（m，n）”函数直观显示单位矩阵的图像。在理解了由0和1两个数据构成的特殊矩阵与其所对应的图像之间的关系后，教师可以布置学生课后尝试利用矩阵构造显示特殊的日期、标语口号等，这与设计大学生军训、运动会汇演的方阵有异曲同工之妙，促进学生所学知识的灵活运用。

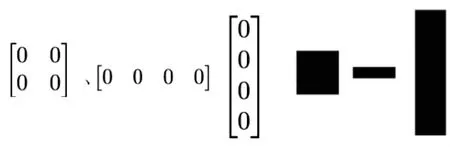
图1 不同阶数的零矩阵图像图

图2 四阶单位矩阵图像图

教师演示两张256像素*256像素的图像与另一张567像素*390像素的图像，通过类比图片的尺寸属性概括出同型矩阵的概念：两个矩阵的行数相等、列数也相等的矩阵称为同型矩阵。如果两个矩阵是同型矩阵，且它们的对应元素相等，那么就称这两个矩阵相等，这就好像是一幅图像复制生成另一幅图像，其图像的属性也是相同的。调用“rand（1，5）”或“rand（5，1）”函数生成元素在（0，1）的随机行矩阵和列矩阵并直观显示如图3所示。在Matlab中调用“A=rand（1，n）”函数生成元素在（0，1）内的1×n随机行矩阵A，再调用“B=diag（A，0）”函数构造以矩阵A的所有元素为主对角元素的对角矩阵，“imshow（B）”函数显示所形成对角矩阵的图像，如图4所示，一整个黑方块的主对角线上分布着不同级别的黑白灰小色块。

图3 行矩阵与列矩阵的图像图

图4 对角矩阵的图像图

Matlab中提供了许多对矩阵操作的函数，例如调用“triu（A）”和“tril（A）”函数可以实现矩阵的上三角矩阵和下三角矩阵的提取，运行后对比效果图如图5所示。通过运行后图像的直观性能够加深学生对定义的理解，初步感受矩阵与图像之间的关联性，上（下）三角矩阵是主对角线以下（上）都是零的方阵，因而图像对应位置会呈现出黑色三角形区域，这也有利于后续上（下）三角矩阵之间的加法、减法、乘法运算及性质的理解。

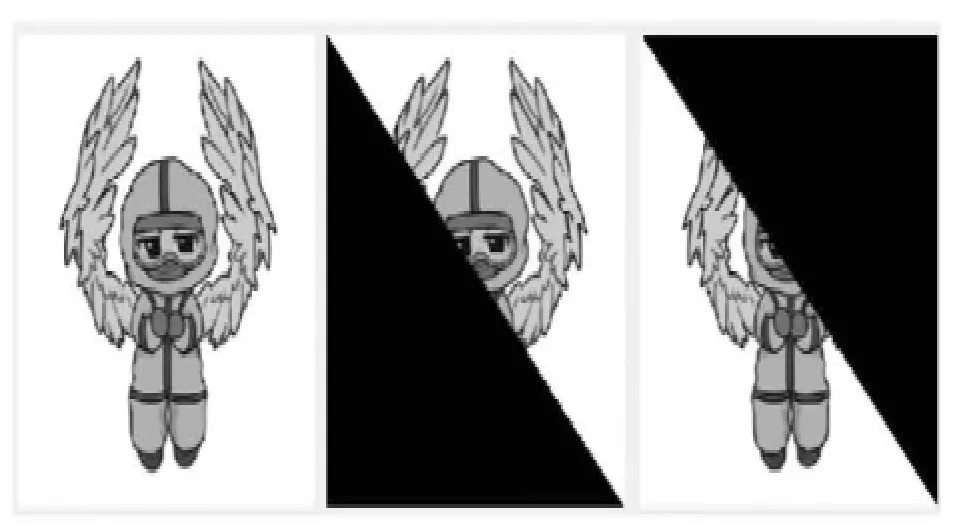
图5 上三角矩阵和下三角矩阵的图像图

（二）从数字图像的角度感受矩阵的运算

矩阵的加法、减法、数乘、乘法运算都是矩阵的基本运算。在教材中往往从“矩阵的本质就是线性方程式”的角度出发理解矩阵的计算规则，这使得教学具有局限性，只能帮助学生将矩阵与线性方程式一一对应理解，不能帮助学生将矩阵的知识与生产实际、科学工程等应用相联系。因此，既要考虑到矩阵计算规则的含义很难理解，又要考虑知识与实践应用的整合，本文研究从数字图像的角度进一步理解矩阵的运算规则、运算性质。

需要与矩阵的运算进行区分的是，在进行图像的像素值相加、相减、相乘等运算时，有可能会出现像素之和大于255的情况，即超出数据类型所允许的最大像素值255，这种情况叫做像素值溢出，一般有归一化和截断两种方法可以解决像素值的溢出问题。归一化是对所有像素值进行统一的放缩，也就是将0～255的范围归一化到0～1的范围。常用的归一化公式是：其中xi和xi*分别表示像素值归一化前和归一化后的值，xmin与xmax分别对应采样数据的最小值和最大值，Pmax是最大可能的像素值，如数据类型是uint8，则Pmax取255，若数据类型为double，则Pmax取1，在Matlab中也可以调用“Y=mapminmax（X，YMIN，YMAX）”函数进行归一化处理。截断是直截了当得将运算后所有溢出的像素值设为该数据类型的最大值。

1.从数字图像的角度感受矩阵的加法

（1）可视水印效果与矩阵的加法

不同图像相加，效果不同，为了防止图片被盗用，一般会在图片上添加水印，来保护图片的版权，通过读取待嵌入水印的图像和水印图像并将两幅图像的大小预处理后进行叠加，实现添加可视水印的效果如下页图6所示，教师在教学过程中还能够潜移默化地开展知识产权教育。

图6 可视水印效果图图7 二次曝光效果图

（2）二次曝光效果与矩阵的加法

两个矩阵的和即这两个矩阵的对应元素相加。图像相加的原理实际就是结合两幅图像的像素内容，即对应像素位置的亮度值矩阵的相加，图像的相加可用于将一幅图像的内容叠加到另一幅图像上去，以达到二次曝光的效果，从而实现增加图片虚幻效果的目的，如图7所示。通过调用Matlab中的“C=imadd（A，B）”函数对两幅图像进行叠加处理，使用的就是截断的方法处理像素值的溢出。选择其中一幅作为前景需要提取主干信息，另一幅则作为背景图将第一幅中提取出的主干信息叠加到第二幅图像中，我们可以发现加法合成之后的画面如图8所示，比之前图像的画面更加明亮。

图8 多重曝光效果图

类比两幅图像相加，读取图像数据后，需要调用“B=imresize（A，[numrowsnumcols]）”函数修改图像，使得它们的大小和尺寸相同，得出只有同型矩阵才能相加的前提条件，更换读取图片的先后顺序，运行结果不变，得出矩阵的加法运算符合交换律的结论。多重曝光效果是指多张照片叠加后的效果，如图9所示，调整三张图像叠加的先后顺序，运行结果保持一致性，可以直观验证矩阵加法的结合律（A+B）C+=A+（B+C），加深学生对矩阵加法运算及运算律的理解。

（3）图像亮度调节与矩阵的加法

图像亮度的调节可以通过矩阵的加法运算实现，将一个正数值（标量）加到一幅图像上，可以增加图像的亮度，调用“B=imadd（A，50）”和“C=imadd（A，100）”函数，使得原图像得每个像素都增加了亮度，运行效果如图9所示。反之，加上一个负数（标量），就会使得图像的亮度降低，效果如图10所示，此时可以类比抛出矩阵的减法运算。

图9 亮度提升效果图

图10 亮度降低效果图

（4）图像的加噪与矩阵的加法

以人脸识别、车牌识别系统为例，受图像采集设备、自然环境等诸多因素的影响，所处理的图像和“本真”图像会产生一定的差异性，这一部分差异就是噪声。因此，要测试算法的稳健性就需要对图像进行加噪处理。实现给图像添加噪声的效果也是通过矩阵的加法实现的，即对各个像素值加上随机量，这是一种常见的加噪方法。调用“B=imnoise（A，” speckle” ，0.03）”函数实现斑点噪声效果如图11所示，其中0.03为可调节的参数，是指均值为0，方差为0.03的均匀分布的随机噪声。

图11 斑点噪声效果图

2.从数字图像的角度感受矩阵的减法

（1）抠除固定背景的底片效果与矩阵的减法

图像的相减常常用于去除一幅图像中诸如背景阴影、周期性的噪声、已知的附加污染等所不需要的加性图案，Matlab中调用“C=imsubtract（A，B）”函数实现从图像中减去另一幅图像的效果，运行后得到抠除固定背景的底片效果如图12所示。类比图像矩阵的加法，图像矩阵的减法也要求同型矩阵才能相减。

图12 抠除固定背景的底片效果图

（2）图像求反与矩阵的减法

调用“D=imcomplement（C）”函数，对图12的运行效果图像的数据进行取反运算，相当于是用一张纯白色的图像与底片效果图做差，从而实现底片反转的效果如图13所示。

图13 图像求反图

（3）目标边缘效果与矩阵的减法

在一些系统设计过程中常常需要计算并确定物体边界位置的信息，可以用图像的减运算实现。以车牌识别系统为例，电子设备在采集图像时，连续拍摄两幅含有车牌的图像，这两幅图像信息不完全对准，也就是在行与列方向上的信息会稍有偏移，这两幅图像之间的减法运算可以得到图像不同方向的相减图像，从而突出图像上定位目标的边缘信息，运行效果如图14所示。

图14 目标边缘效果图

3.从数字图像的角度感受矩阵的数乘

还有一种常见的图像处理操作是一幅图像与一个常数的乘法运算，实质上就是矩阵的数乘运算，矩阵的数乘运算是矩阵中的每一个元素都乘以常数，这个常数被称为缩放因子。运算过程中，调用“B=immultiply（A，k）”函数实现，如果使用的缩放因子k大于1，灰度值会增加，那么图像的对比度和亮度将提升，这里分别展示了乘以缩放因子2和4以后的图像，运行结果如图15所示，反之，如果使用的缩放因子k小于1则灰度值会降低，使得图像的对比度和亮度降低，这里分别乘以缩放因子0.8和0.2以后的图像如图16所示。通常，通过缩放处理产生的图像亮度的调节效果比直接添加像素偏移值更为自然，既能够呈现图像的拍摄主体，图像又不会失真，这主要取决于其处理时能够较好地维持图像的相关对比度。