不同坡度下扭王字块斜坡堤胸墙受力的试验研究
2022-02-25孙大鹏邢晨曦相才康
孙大鹏,邢晨曦*,相才康,董 胜,刘 飞
(1.大连理工大学 海岸与近海工程国家重点实验室,大连 116024;2.中国海洋大学,青岛 266100;3.长春中海地产有限公司,长春 130000)
近年来,众多中外学者从多种角度对斜坡堤的胸墙受力开展研究。MARTIN[1]研究发现在无块体掩护的区域,胸墙上的压强是均匀分布的,与波浪在堤顶处的厚度线性相关;李雪艳[2]设计了前仰式、深弧式、后仰式和直立式等多种形式的胸墙,探究影响斜坡堤胸墙受力的因素;在波浪不发生破碎的条件下,FENTON[3]给出了一个波浪力作用在胸墙的计算方式;SANG[4]研究了斜入射波浪条件下顶墙上波浪荷载的变化。基于实验数据的分析,提出了斜入射波作用下水平力和垂直力相关估算公式;王颖[5]开展多种形式防浪墙的斜坡堤断面物模试验,对不同形式墙体的波浪力和稳定性展开详细的研究与讨论。《港口与航道水文规范》[6]给出斜坡堤无掩护块体时胸墙平均压力强度的计算式;许凡[7]开展模型试验,研究了多种波浪参数以及护面块体对波浪力的影响。潘兴凯[8]探究堤顶胸墙的受力特征,发现胸墙受到的波浪力受波高、水深、周期等因素的影响,同时给出扭王字块掩护下波浪力折减系数;翁克勤[9]通过对苏伟东[10]等人的研究成果进行总结,讨论分析了护面块体、坡肩宽度、波陡等因素对斜坡堤所受波浪力的影响;柳玉良[11]探究了在护面块体的情况下斜坡堤胸墙波浪力的折减情况,发现部分物理模型试验数据与《防波堤设计与施工规范》[12]、《港口与航道水文规范》[6]中的计算方式有差异,籍此,柳玉良[11]系统研究了胸墙存在护面条件时所受到的波浪力折减情况。
扭王字块斜坡堤作为常见的斜坡堤被广泛应用,但规范[6]没有明确给出扭王字块斜坡堤胸墙所受波浪力计算公式。刘飞[13]分析了相对堤顶超高、相对坡肩宽度、相对水深、相对胸墙高度、波陡和相对块体尺寸等因素,针对m=1.5的扭王字块斜坡堤,依据物理模型试验,给出了胸墙受力的计算关系式。本文将在此基础上,开展不同坡度的试验研究,得出扭王字块体斜坡堤胸墙受力完整计算公式,旨在丰富规范内容并为斜坡堤设计提供参考。
1 试验概况
1.1 模型和试验条件
物理模型试验在大连理工大学海岸和近海工程国家重点实验室开展,试验使用的造波水槽长宽高尺寸依次为50 m、3 m、1 m,在距离造波板30 m处安置试验模型,如图1所示。水槽另一端安放消波装置用于消波。试验的造波装置采用液压伺服系统,产生模型试验所需的不规则波,其中波谱是JONSWAP谱,γ= 3.3。

图1 试验模型示意图
斜坡堤模型断面结构见图 2和图3,斜坡堤的护面块体为扭王字块,d为堤脚前的水深;斜坡坡度系数为m,且1≤m≤2.5;Hc′为堤顶超高(水槽静水位到斜坡堤顶的高度);b1为胸墙前坡肩的距离;胸墙的高度用P表示。

图2 模型结构断面示意图 图3 模型试验图
物理模型试验中,坡度系数m分别取值1.5、2.0、2.5 ,相对坡肩宽度(b1/Hs)的取值区间为 0.6~2.0,相对水深(d/Hs)的取值区间为 2.2~8.0,相对胸墙高度(P/Hc′)的取值区间为 0.4~1.0,相对堤顶超高Hc′ /Hs)的取值区间在0.8~1.6,波陡(Hs/L)的取值区间是0.02~0.06,扭王字块体相对尺寸(h/Hs)的取值区间为0.32~1.30。试验所使用的块体皆满足稳定性要求,块体的模型尺寸h依次是42 mm、60 mm、65 mm、78 mm,如图4所示。块体随机摆放,块体摆放密度均符合规范要求。

图4 护面块体结构示意图
1.2 试验工况
采用m=1.5、2.0、2.5的3种试验坡度,每种坡度分别针对光滑混凝土板和4种尺寸扭王字块体开展胸墙受力试验,计有15种坡度和块体的组合,每种组合分别有16种试验工况,工况如表1所示。
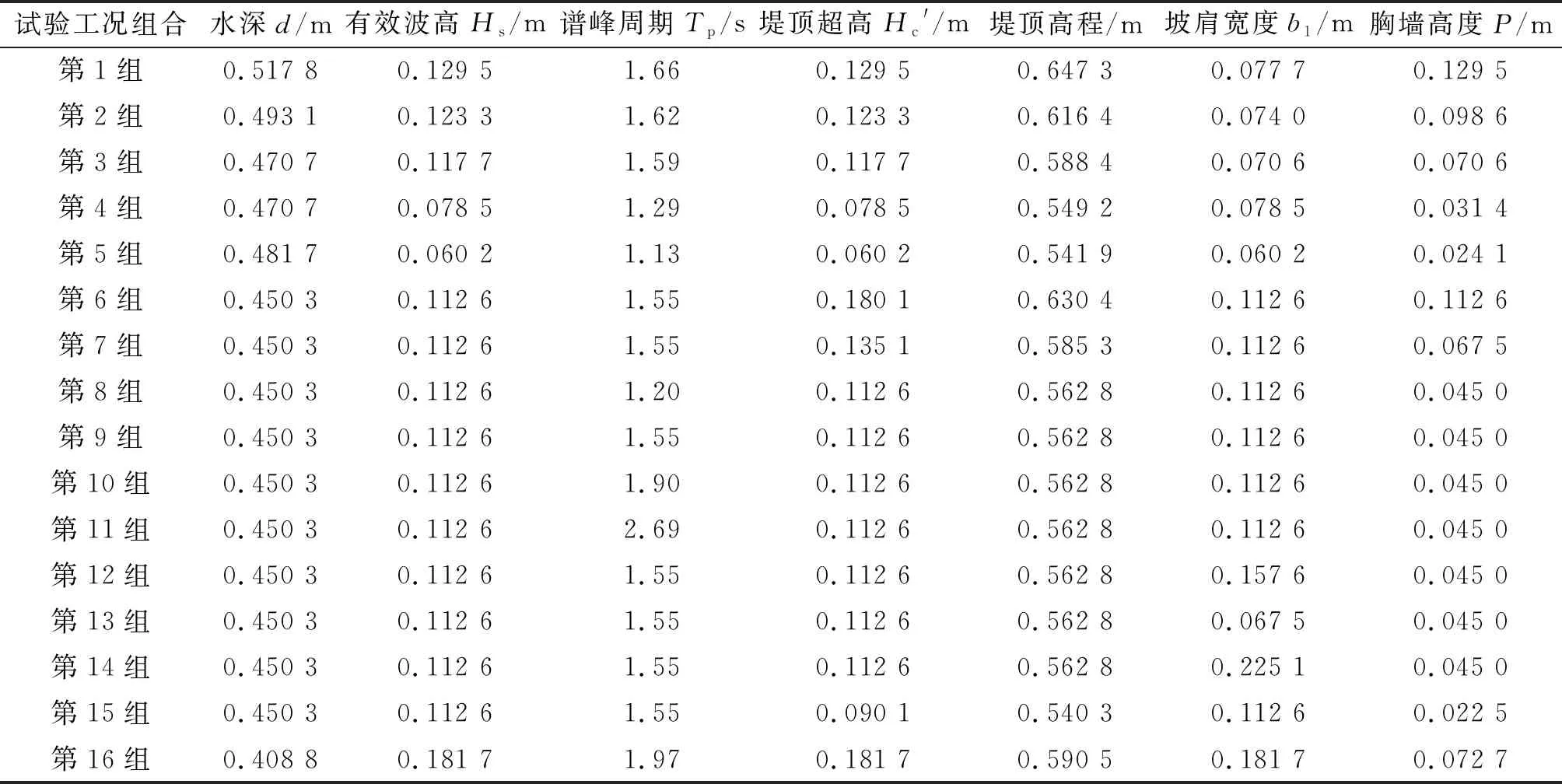
表1 试验的工况
1.3 波浪力采集
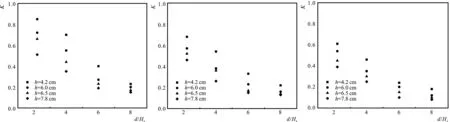
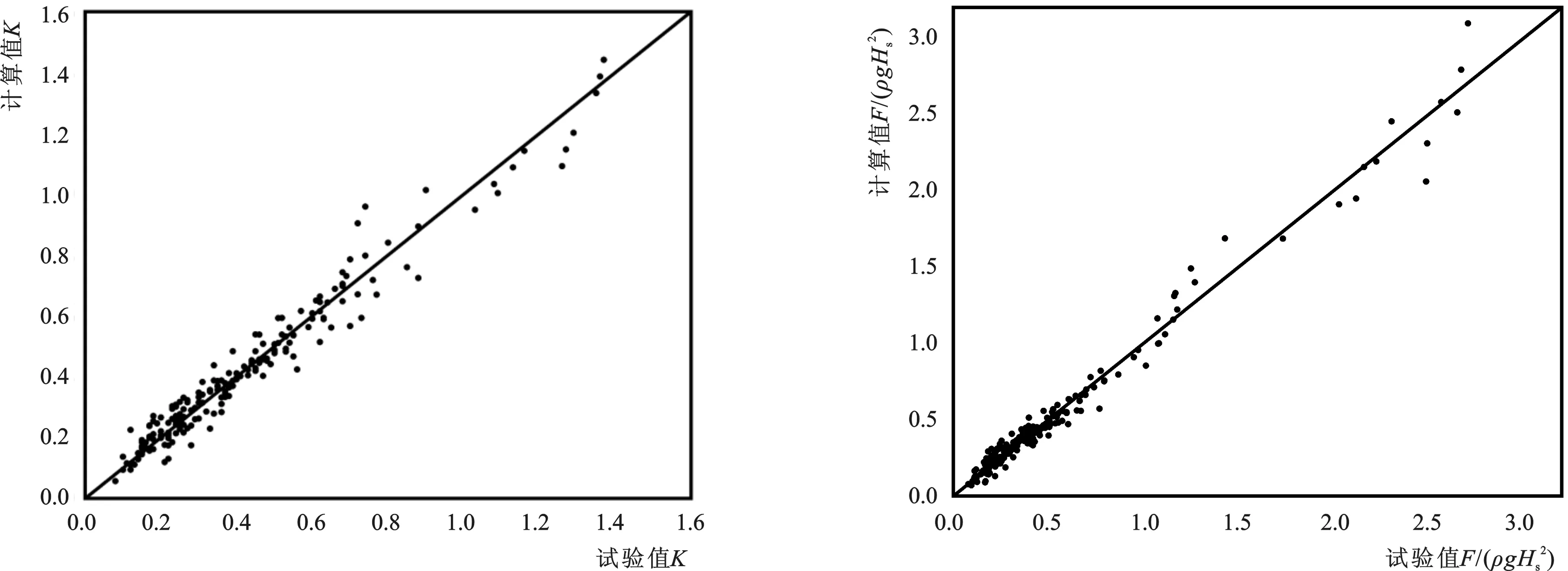
为保证各组试验不规则波波数不小于100个,物理模型试验时,造波时长分别采用328 s(Tp﹥2.0 s)和164 s(0 s 图5 点压力测量装置(单位:mm) 遵循规范[6,12]的编制思路,前期进行光滑混凝土板斜坡堤胸墙水平波浪力物理模型试验,综合考虑胸墙受力的主要影响因素(包括斜坡坡度、相对胸墙高度、波陡等六种因素),运用π定理,给出光滑混凝土板斜坡堤胸墙所受水平波浪力的无因次表达式 (1) 式中:L为波长,m;Hs为有效波高,m;F板为混凝土板斜坡堤胸墙所受水平力,N/m。 当Hs/L在0.02~0.06区间时,保持其他影响因素不变,仅改变Hs/L的数值,当波陡的值变大时,F板/(ρgHs2)随之变大后变小,二者选用二次函数拟合,如图6所示。 图6 Hs/L对F板/(ρgHs2)的影响 图7 d/Hs对F板/(ρgHs2)的影响 保持其他影响因素不变,当相对水深的取值区间为2.2~8.0时,仅改变d/Hs的数值,d/Hs与F板/(ρgHs2)呈正相关性,选用指数函数拟合,如图7所示。 保持其他因素不变,相对堤顶超高的取值范围为0.8~1.6时,随着Hc′/Hs增大,对应F板/(ρgHs2)增大,如图8所示,二者呈正相关性,选用线性函数拟合。 图8 Hc′/Hs对F板/(ρgHs2)的影响 图9 b1/Hs对F板/(ρgHs2)的影响 当相对坡肩宽度的取值范围是0.6~2.0时,保持其他影响因素不变,如图9所示,随着相对坡肩宽度的取值增大,对应F板/(ρgHs2)增大,二者呈线性函数关系。 在P/Hc′的取值范围是0.4~1.0时,保持其他影响因素不变,仅调整相对胸墙高度的大小,F板/(ρgHs2)大小随之改变,如图10所示,二者呈正相关性,选用指数型函数拟合。 图10 P/Hc′对F板/(ρgHs2)的影响 图11 m对F板/(ρgHs2)的影响 当1.5≤m≤2.5时,保持其他影响因素不变,仅调整m的取值,F板/(ρgHs2)随之改变,二者呈指数关系,如图11所示。 依据上述2.1~2.6节的分析结果,运用多元非线性回归拟合的方法,得出混凝土板斜坡堤胸墙受力的无因次计算公式 (2) 式(2)计算值、规范计算值(引自刘飞[13]的规范计算值)和模型试验值三组数据的比较如图12所示。由图可见,式(2)的计算数据较为接近试验数据。公式值和试验数据匹配度较好。式(2)的相关系数较高(R>0.9),公式具有较好的相关性。 图12 F板公式值和物模试验值关系 综合考虑波陡、相对堤顶超高、坡度、相对胸墙高度、相对水深、相对块体尺寸及相对坡肩宽度等因素,并且依据π定理,总结出扭王字块斜坡堤K的表达式 (3) (4) 式中:F为扭王字斜坡堤胸墙所受水平波浪力,N/m;K为胸墙所受水平波浪力的结构折减系数,等于在其他工况因素相同的情况下F与F板之比。 当Hs/L在0.02~0.06区间时,保持其他影响因素不变,仅改变波陡的大小,K值随之改变,如图13所示,采用指数型函数对二者进行拟合。 13-a m=1.513-b m=2.013-c m=2.5 当d/Hs在2.2~8.0区间范围时,控制其他影响因素不变,仅改变相对水深的大小,K值随之改变,如图14所示,无因次变量d/Hs和K呈负相关,选用指数函数拟合。 14-a m=1.514-b m=2.014-c m=2.5 保持其他影响因素不变,只调整相对堤顶超高的数值大小,K值随之发生变化。当Hc′/Hs取值范围在0.8~1.6时,无因次变量Hc′/Hs与K呈线性关系,如图15所示。 15-a m=1.515-b m=2.015-c m=2.5 保持其他因素大小不变,只调整b1/Hs的数值,K值随之改变,如图16所示。当b1/Hs的取值范围是0.6~2.0时,无因次变量b1/Hs与K采用指数函数拟合。 16-a m=1.516-b m=2.016-c m=2.5 当P/Hc′的取值范围在0.4~1.0时,控制其他因素大小不变,只调整P/Hc′的数值,K值随之改变,如图17所示,二者选用指数型函数拟合。 17-a m=1.517-b m=2.017-c m=2.5 由图17所示,当P/Hc′值为1,护面结构的折减系数均超出1,大于规范[12]所规定的0.6~0.7区间。当P/Hc′值为1时,同期试验测量的胸墙受力和平均越浪量数据如表2所示。根据数据分析发现,当混凝土板斜坡堤P/Hc′=1时,越浪量越大,胸墙受力越小;而扭王字块斜坡堤P/Hc′=1时,块体的消浪属性使越浪量减小,因此波浪集聚在胸墙上,导致胸墙水平波浪力变大,发生了K>1的现象,此类情况在苏伟东[10]、孙大鹏[14]的试验研究中也存在,故带护面块体情况下的斜坡堤工程设计中,建议胸墙受力的折减系数谨慎取值。 表2 平均越浪量值和胸墙受力值 保持其他影响因素不变,仅调整h/Hs的大小,K值随之改变。在图示区间内,h/Hs与K值呈负相关性,二者选用指数函数拟合,如图18所示。 图18 h/Hs对K的影响 (Hs/L=0.03; 图19 m对K的影响(Hs/L=0.04; 保持其他影响因素不变,只调整m的大小,试验结果如图19所示。表明1.5≤m≤2.5时,随相对胸墙高度m增大,K值减小,K与m呈线性函数关系。 规范[12]建议扭王字块护面结构的折减系数K在0.6~0.7范围内取值。本文研究发现,折减系数K的值并不局限在此区间范围,如图19所示,坡度因素也对折减系数K的取值也有较大的影响。 依据上述的试验数据分析,运用多元非线性拟合方法,给出折减系数K的计算关系式 (5) 公式值与试验值对比结果如图20,相关系数R>0.90,说明式(5)的计算值和试验值相关性较强。 图20 模型试验值K与公式值K对比 图21 F计算值与物模试验值对比 综合考虑了斜坡堤胸墙水平波浪力的主要影响因素,包括斜坡坡度、相对坡肩宽度和相对水深、相对块体尺寸、波陡、相对堤顶超高、相对胸墙高度等,延续规范编制思路,进而得到扭王字块斜坡堤胸墙所受水平波浪力的关系式 (6) 式中:折减系数K由式(5)所得。 式(6)的计算值和模型试验结果的对比结果如图21,两组数据在y=x两侧分布均匀,相关系数R>0.90,因而式(6)的可靠度较好。 (1)鉴于规范[6]没有明确给出扭王字块护面斜坡堤胸墙水平力的计算公式。本文综合考虑斜坡坡度、相对坡肩宽度、相对胸墙高度、波陡、相对水深、相对块体尺寸和相对堤顶超高等影响因素,系统开展扭王字块斜坡堤胸墙水平波浪力的物理模型试验,基于单变量分析法和多元非线性拟合法,拟合出了不同坡度下胸墙水平波浪力的计算关系式,并与模型试验值进行比较,表明本文提出的计算公式有较好的可靠性,试验成果丰富了规范内容,能给工程设计参考使用。 (2)规范[12]中对于扭王字块体护面结构的折减系数,建议取值区间为0.6~0.7。本文通过试验研究发现,护面结构的折减系数受波浪要素、堤型结构和护面块体等因素影响,K值并不只局限在此区间范围内。这一认知同刘飞[13]的试验结果一致。同时,本文研究发现K值随坡度系数m的改变而变化,即坡度亦是扭王字块体斜坡堤胸墙水平力的折减系数的主要影响因素之一。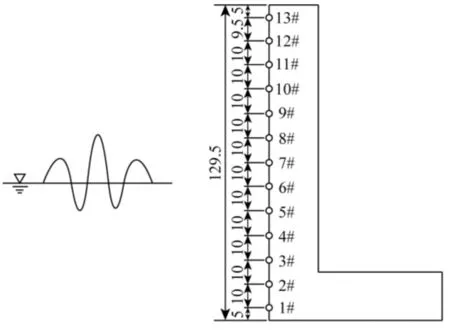
2 混凝土板斜坡堤胸墙水平波浪力的试验结果
2.1 波陡Hs/L的试验分析

2.2 相对水深d/Hs的试验分析
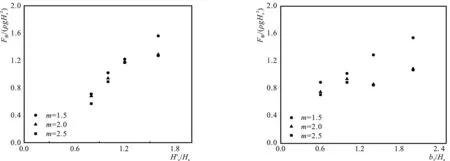
2.4 相对坡肩宽度b1/Hs 的试验分析
2.5 相对胸墙高度P/Hc′的试验分析

2.6 坡度m的试验分析
2.7 F板/(ρgHs2)的计算关系式

3 扭王字块斜坡堤胸墙水平波浪力折减系数的试验结果
3.1 K与波陡Hs/L之间的关系

3.2 K与相对水深d/Hs之间的关系
3.3 K与相对堤顶超高之间的关系

3.4 K与b1/Hs之间关系

3.5 K与相对胸墙高度P/Hc′ 之间的关系
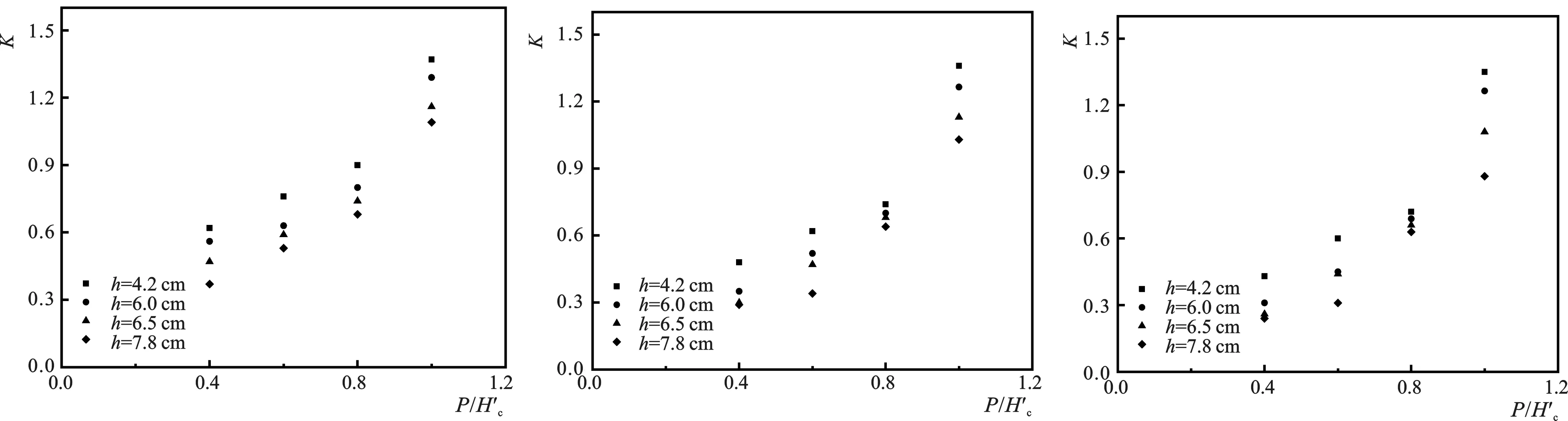

3.6 相对块体尺寸h/Hs对K的影响
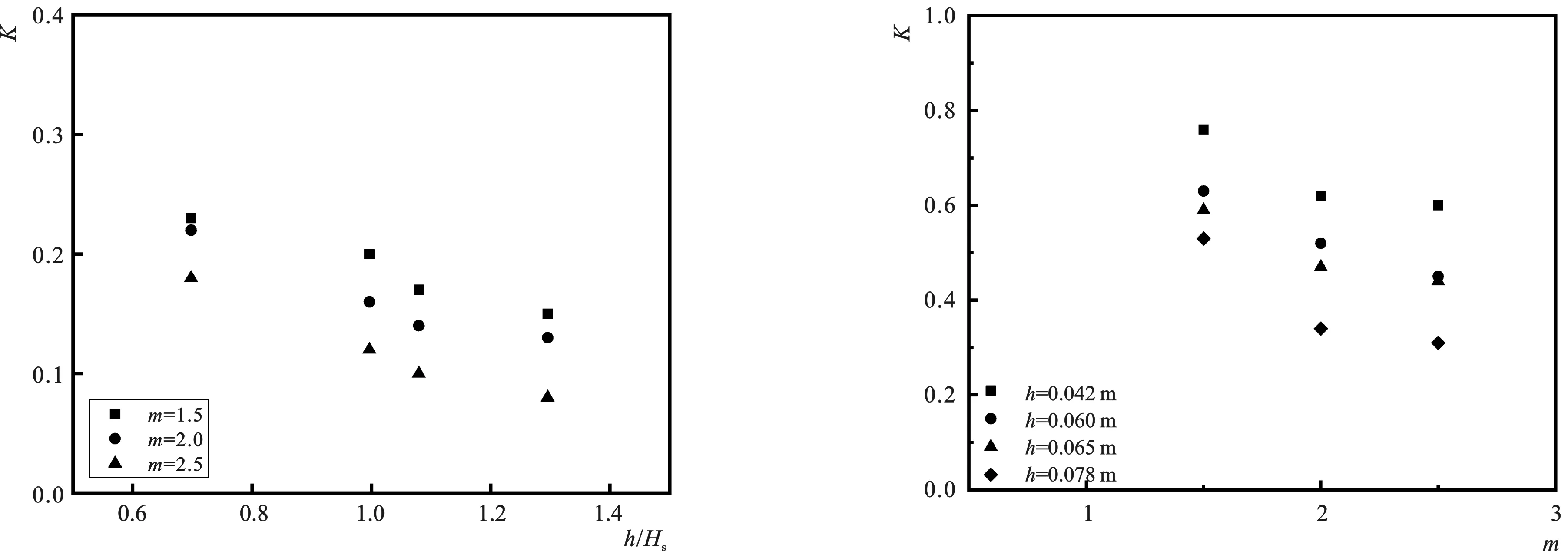
3.7 K与坡度m之间的关系
3.8 K的计算关系式
4 扭王字斜坡堤胸墙水平波浪力计算公式
5 结论
