不同粒径组合方式抛石群水下运动扩散规律

张 伟，王春磊，李卫国，王瀚锐，李小超，常留红

(1.中交天航港湾建设工程有限公司，天津 300450；2.湖南省水运建设投资集团有限公司，长沙 410011；3.长沙理工大学 水利工程学院，长沙 410114)

抛石群水下运动扩散是河道治理[1]、护岸、潜丁坝、桥墩防冲等实际工程中经常遇到的问题之一[2]。抛石施工受环境因素影响较明显，既有一定的规律性，又呈现出一定的随机性，一直是工程界关注的热点问题之一，目前尚难找到适应于各种水下抛石的施工工艺。

以往抛石运动的研究主要关注相关经验公式，如早期苏联学者伊兹巴斯通过平堵截流模型试验提出目前工程最常用的伊兹巴斯公式[3]、考虑水深的沙漠夫公式[4]以及姚仕明[5]、毛佩郁[6]、韩海骞[7]、姚仕明[8]等学者推导的抛石漂移的相关公式。此外，还有不少学者研究了抛石水下的运动过程。陈凯华等[9]分析了水下抛石运动规律以及抛石基床的堆积情况。刘晓青[10]等通过物理模型试验研究散抛块石种类、尺寸及水流速度对块石漂移量的影响。张宏千[11]等通过对水流运动中的透水框架受力分析，推导了不同搭接和抛投方式的透水框架在不同抛投高度的落距公式。刘卡等[12]基于计算流体力学与离散元法耦合的方法，从抛石初始速度和抛石粒径等方面模拟了抛石水下运动过程。王茂枚等[13]通过河床结构的异质性,从粒子随机运动角度解释了抛石在河道中反常输运的物理机理。李小超等[14]通过开展模型试验，分析了不同因素对抛石漂移距离的影响，并导出了相应的计算公式。还有学者通过开展现场试验，探究涨、落潮条件下抛石水下运动的影响因素，并推导抛石漂移距离公式。但鲜有关于抛石群水下扩散规律的研究。

抛石群水下运动扩散是影响抛石成型及其稳定的重要因素。依托长江干线武汉至安庆段6 m水深航道整治工程，基于OpenFOAM建立抛石水下运动三维流固耦合数学模型，研究不同粒径组合方式抛石群水流方向漂移距离、抛石群落点分布，揭示抛石群水下运动扩散规律。对水下抛石质量控制和成本控制具有重要的理论和现实意义，研究成果可在类似工程推广应用。

1 工程概况

工程河段上起小孤山，下至华阳河口，长30 km，为分汊河型，南汊为主汊，较顺直，为主航道所在。北汊为支汊，又称为马当圆水道，分流比很小，河道弯曲、狭窄，进口已淤浅至航行基面以上。南汊分为3个水道：马当矶以上为马当南水道，江心有心滩——棉外洲；马当矶—娘娘庙为马当阻塞线水道(以下简称马阻水道)，被瓜子号洲再度分为两汊，右汊为主汊及主航道；娘娘庙以下为东流直水道。马当南水道右岸为江西省彭泽县，左岸为江西省彭泽县棉船镇，上起小孤山，下至马当矶，长约13 km，为受节点控制的二级分汊河段，江中棉外洲分水道为左右两槽，右槽为主航槽较为窄深，左槽相对宽浅。马当南水道上接东北水道，下连马阻水道。东流水道位于长江下游九江—安庆河段，上起华阳河口，与马当水道相连，下迄吉阳矶，与官洲水道相接，全长约31 km。工程的主要建设内容包括马当河段棉外洲顺坝加高工程、棉外洲中部护滩工程、左槽中段潜坝工程、瓜子号洲右缘护滩带工程以及疏浚工程和东流水道天玉串沟控制工程。工程主要工作量包括：棉外洲顺坝加高工程抛石50 570 m3；左槽中段潜坝工程抛石280 646 m3；瓜子号洲右侧中部护滩带工程8#护滩带抛石89 002 m3；瓜子号洲右侧中部护滩带工程9#护滩带抛石80 544 m3；瓜子号洲右侧中部护滩带工程10#护滩带抛石100 808 m3；天玉串沟控制工程1#护底带抛石69 720 m3；天玉串沟控制工程2#护底带抛石70 948 m3。

根据实测水文资料，本工程所处水域大多为主流顶冲水域，实测流速一般在1.7 m/s左右，最大为1.98 m/s。施工过程中抛石建筑物附近的局部水流结构不断被改变，如果断面抛投成型质量不能保证，在高流速、大水深条件下很容易出现稳定性不足、发生水毁等问题。混合石料抛投成型过程影响因素复杂，抛石群体下落过程的漂移和分层等现象使混合石料抛投断面形态及级配组成随之变化，直接影响断面稳定性，因此有必要对混合石料群体抛石水下运动过程及落至底床上的分布形态进行研究，为抛投施工稳定性分析提供依据。本文采用CFD-DEM耦合方法对群体抛石水下运动过程进行模拟，探讨抛石群落至底床上的分布形态和级配组成。

2 数值模型的建立

2.1 流体运动控制方程

流体运动的控制方程为局部平均的不可压缩Navier-Stokes方程

(1)

(2)

2.2 颗粒运动控制方程

固体运动采用牛顿第二定律进行求解，其控制方程如下

(3)

(4)

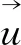
2.3 固体颗粒间的作用控制方程

考虑块石之间的接触具有较强的非线性，采用软球模型对块石颗粒之间碰撞过程进行模拟，块石颗粒之间的接触力采用非线性弹簧-阻尼模型计算，该模型在Hertez弹性接触理论的基础上考虑粘弹性影响，将块石之间的接触力沿法向和切向分解为两个分量，其表达式分别为

(5)

(6)

(7)

(8)

(9)

(10)

式中：Ei和Ej分别为块石i和块石j的弹性模量，vi和vj为相应块石的泊松比。

颗粒间的润滑力采用Ball-Melrose模型进行计算，该力与颗粒间的相对速度成正比，与颗粒间的距离成反比。

2.4 流体与颗粒间作用力控制方程

(11)

拖曳力根据下式计算

(12)

升力由下式计算

(13)

附加质量力根据下式计算

(14)

Basset历史应力为两相流中颗粒与流体存在相对加速度时所产生的一种非恒定流体力，其表达式

(15)

2.5 参数选择及网格划分

计算域尺寸为16 m×10 m×15 m(长×宽×高)，原点设置于0号点处，水流沿X方向流动，如图1所示。采用有限体积法对计算域进行离散，网格划分采用结构化六面体网格进行，网格尺寸根据实际块石粒径确定。根据不同网格尺寸的试算结果，网格尺寸与块石颗粒直径的比值确定为2～3的范围。流体边界在OpenFOAM内设置为：入流边界(面0374)、出流边界(面5621)、前侧边界(面0123)、后侧边界(面7654)，底部为无滑移边界，顶部为滑移边界。固体颗粒边界在LAMMPS内设置为：入流边界、出流边界、前侧边界、后侧边界，顶部和底部边界为固定边界。流体和颗粒的入流边界与出流边界互为连续性周期边界，前侧边界和后侧边界互为连续性周期边界。块石密度2 650 kg/m3，泊松比为0.3，弹性模量为3.755×104MPa，剪切模量为1.444 2×104MPa。为了验证数值模型的正确性，图2将计算得到的单一块石漂距值与实验室水槽试验得到的块石漂距值[14]进行了比较，数值计算得到的块石漂距变化规律与实验结果整体上一致，均表现为随着块石质量(或块石粒径)的增大而逐渐减小，计算值较实验平均值略微偏大。

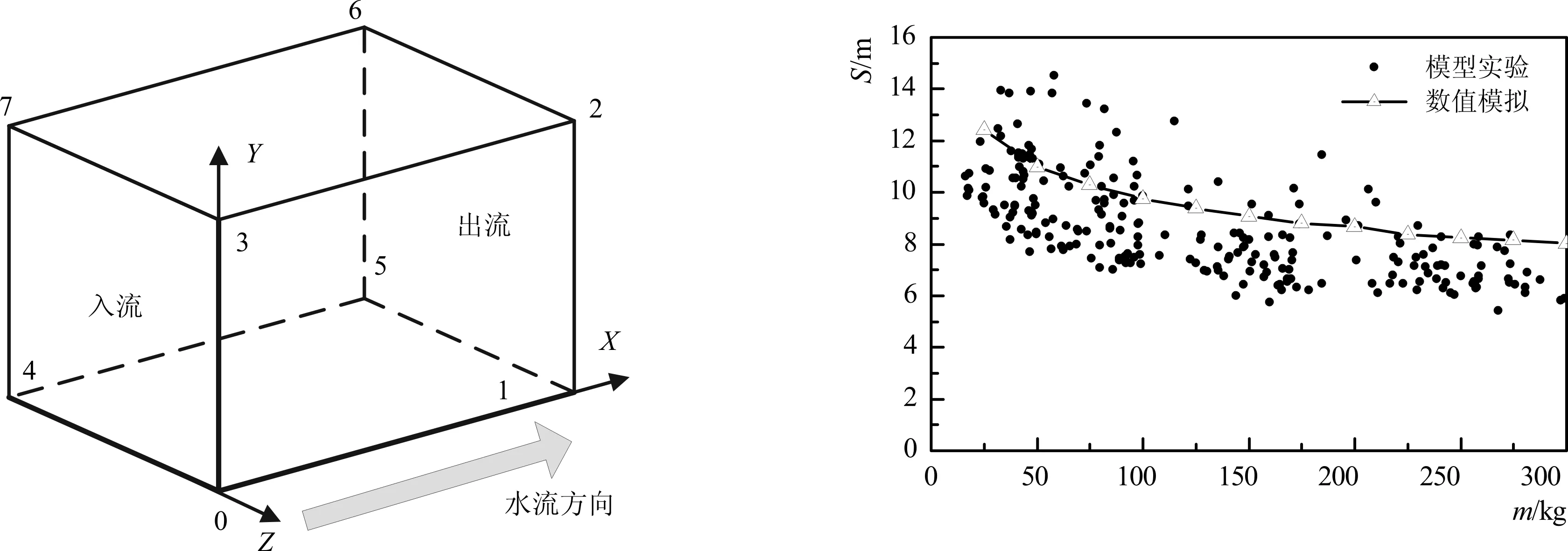
图1 数值水槽示意图 图2 单一块石漂距计算值与模型实验[14]的比较

3 抛石群扩散运动规律分析

为了考察块石颗粒群中颗粒级配的影响，采用两种粒径组合方式块石颗粒组合进行模拟计算。块石颗粒排列矩阵参数见表1，表1中块石1代表粒径较大的块石，块石2代表粒径较小的块石。

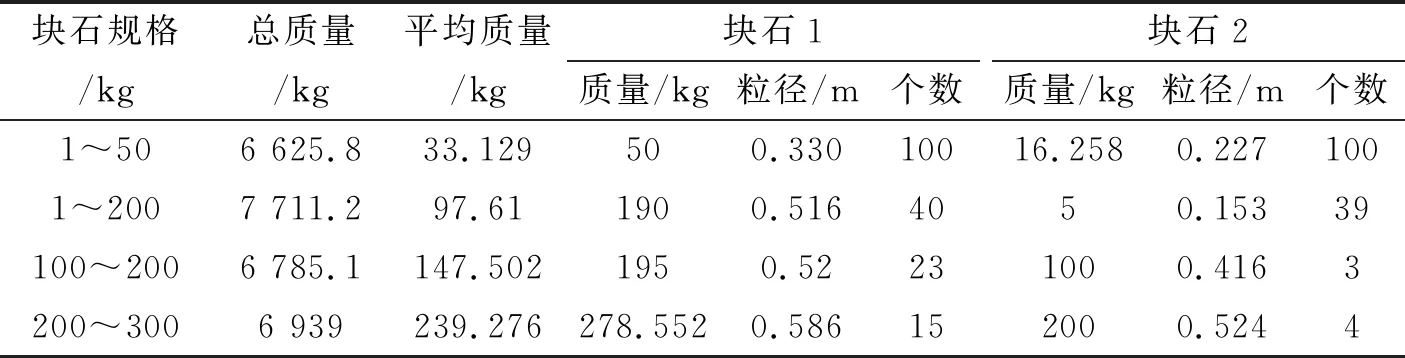
表1 不等直径颗粒组合块石参数

3.1 抛石群水流方向漂距分析

块石颗粒群在水流方向上漂距随时间变化如图3所示，块石颗粒群的平均漂移速度随块石平均质量的减小而增大，且质量越小，块石群的下落时间越长。

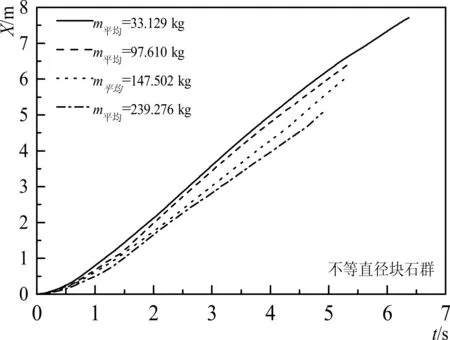
图3 不同粒径组合方式块石群水流方向漂距随时间变化

3.2 抛石群落点分布分析

图4为不同时刻块石群在水中状态，块石群前端的下落速度比后端慢，个别块石的下落速度比块石群整体速度大。图5为不同粒径组合方式块石组合颗粒群落至底床上的落点分布，图中um为表面流速，流速垂向分布为指数为1/12的指数分布。块石颗粒群落至床底后的分布形状较不规则。虽然质量不同，但由于颗粒间的相互影响，并非质量小的漂距远，质量大的漂距近。块石颗粒群分散之后，并未出现单一质量块石集中在一起的现象，而是呈现大小块石夹杂在一起的分布规律。受块石运动的影响，块石群所在区域的流速减小，这是由于流体质点将动能传递给块石引起的。

4-a t=0 s4-b t=0.5 s4-c t=1.5

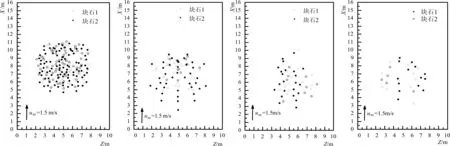
5-a m平均=33.129 kg5-b m平均=97.61 kg5-c m平均=147.502 kg5-d m平均=239.276 kg

4 结论

基于计算流体力学程序OpenFOAM和离散元程序LAMMPS建立水下抛石三维流固耦合数学模型，分析抛石群扩散运动规律，得到以下主要结论：(1)不同粒径组合方式块石颗粒群的平均漂移速度随块石平均质量的减小而增大，且质量越小，块石群的下落时间越长。(2)不同粒径组合方式块石组合颗粒落至床底后，并未出现单一质量块石集中在一起的现象，而是呈现大小块石夹杂在一起的分布规律。