一种适用于高渗透率主动配电网的电能质量调节器

徐艳春， 樊士荣， 谢莎莎， MI Lu

(1.三峡大学 梯级水电站运行与控制湖北省重点实验室，湖北 宜昌 443002； 2.国网吉林省电力有限公司长春供电公司，吉林 长春 130000； 3.德克萨斯农工大学 电气与计算机工程系，美国 德克萨斯 77840)

0 引 言

随着新能源的接入，分布式发电在配电网中的渗透率日益提高，由于分布式能源的随机性、间歇性以及大量电力电子器件的接入对传统电网造成了巨大影响，造成了严重的电能质量问题[1-3]。而这些电能质量问题的处理方案依然有待讨论。

分布式电源接入电网的容量相对较小且随机，对其可能产生的每种扰动都加入专门的电能质量治理器成本较高，需要相较更加灵活的治理手段，例如专门处理电压幅值扰动的动态电压恢复器(dynamic voltage restorer，DVR)，仅能有效处理幅值扰动如电压跌落、善变、振荡等。有源电力滤波器是目前使用比较广泛的电能质量治理手段，包含串联有源滤波器、并联有源滤波器、混合有源滤波器。统一电能质量控制器(unified power quality conditioner，UPQC)[4-5]综合了上述滤波器的优点，对电压、电流等电能质量问题均有良好的调节能力。UPQC由并联补偿部分与串联补偿部分组成，并联部分主要补偿由非线性负载引起的电能质量问题；串联部分通过向配电系统中注入连续可变的电压分量来消除电压幅值的波动。两组逆变器之间使用直流环节级联，整体来说结构较为复杂。并且，如果想妥善治理谐波问题，UPQC需要检测和跟踪谐波电流，这不仅对于系统中的谐波检测装置提出了非常高的要求，也使控制系统的设计难度增加。而从控制方法而言，目前虽然线性控制方法依然为主流，但依然存在许多弊端，例如最常见的PI或PID控制系统依赖于参数的针对性选取[6-7]，泛用性、灵活性大打折扣，限制使用场景；又例如空间矢量调制(space vector pulse width modulation，SVPWM)[8-9]，虽然降低了对参数设置的依赖性，输出的准确度也合乎要求，但这类算法基于旋转坐标系，算法计算量大，复杂程度高，延迟也相对较高，具体应用中还需要优化。

本文使用的电能质量调节器结构基于串联型有源滤波器对上述提及问题存在较大优势，其结构相对于UPQC而言相对简单，对系统中的检测量要求较少，且其自身结构对谐波呈励磁阻抗、对基波呈短路阻抗、对谐波具有隔离作用，再结合简单的无源滤波器即可完成谐波治理，在复杂环境下更具优势，近年来，对其优异特性已有相当多的研究[10-13]，但是目前的研究多集中于其控制方法，这些控制方法需要针对不同的问题做不同的参数设置，灵活性欠佳，且目前的研究鲜有与高渗透率主动配电网结合，对各类电能质量扰动进行治理的工作也较少。因此本文的控制方法选择采用有限控制集模型预测控制(finite control set model predictive control，FCS-MPC)，该方法是在模型预测控制(model predictive control，MPC)的基础上加入非线性约束条件实现的，目前该方法在诸多领域有广泛应用，例如，文献[14]中将其用于配电网的优化调度；文献[15-16]中将其用在电机传动领域，保障永磁同步电机系统的平稳可靠运行；该方法也被用于电力电子器件，如逆变器进行控制，如文献[17-18]；但是，由于权重因子的确定问题，原始的FCS-MPC对多目标优化问题并不友好，在高渗透率主动配电网中的电能质量扰动多为复合扰动，只考虑幅值扰动或是频率尤其是谐波扰动都是不充分的，因此本文根据建立的串联型有源滤波器的数学模型与约束条件对结果进行不断地修正，并对成本函数进行了重新设计，使最后的输出结果可以依据幅值扰动与谐波扰动的剧烈程度进行判断，最终实现最优开关状态输出。起到对电能质量进行治理的作用，无论在计算量还是复杂度都优于上述提及的方法。

本文将串联型有源滤波器与FCS-MPC相结合，得出一种基于可调电抗器的新的电能质量综合治理方法，针对串联型有源滤波器中的磁通结构以及输入、输出特点对FCS-MPC进行了重新设计，依据电压、电流的幅值以及谐波畸变率自适应确定权重参数，并对幅值扰动、谐波等问题进行具体分析并治理，目前该结构与进阶过程控制方法结合的尝试还不充分，同时，也对其隔离谐波的优良特性进行阐述；为了验证所提方法的可行性，本文搭建以IEEE 13 节点工业平衡负载配电网为基础的高渗透率主动配电网的仿真模型实验平台，在光伏、燃料电池接入下所产生的扰动信号进行治理，并对该背景下各个节点的谐波畸变率进行分析，表明本文所提的方法并不受鼹鼠效应(“whack-a-mole” effect)的影响[19]，进一步证明该方法的有效性。

1 串联有源滤波器基本结构及原理

串联型有源滤波器的结构如图1所示，其由变压器、逆变器以及恒定直流源组成，仿真中的恒定直流源为一理想直流源，直流源的电压幅值应高于变压器二次侧的电压最大值，本文中的直流源电压取400 V。在进行试验时，直流母线电压可以由一个不控整流器产生。该系统的控制原理为磁链控制，如果每个采样时间内向变压器二次侧注入合适的电压，一次侧电流和二次侧电流亦会随之变化，从而达到改变磁链与变压器阻抗的目的，此时的变压器为一个双边励磁系统。

图1 串联型有源滤波器结构Fig.1 Structure of series power quality regulator

根据串联型有源滤波器中的变压器T型等效电路，如图2所示，变压器两侧的电压模型可表示为：

图2 有源滤波器中变压器T型等效电路Fig.2 T-equivalent circuit of transformer

(1)

(2)

式中：v1(k+1)、v2(k+1)为变压器下一个采样时间的一次侧以及二次侧电压；i1(k)、i1(k+1)为变压器该时刻与下一时刻的一次侧电流；i2(k)、i2(k+1)为变压器该时刻与下一时刻的二次侧电流。

2 有限控制集模型预测控制

在众多控制方法中，模型预测控制有其独到的优势，其无需级联回路可实现多目标控制，可以通过改变成本函数来控制输出，也可以在不改变硬件配置的情况下通过改变成本函数来升级控制系统。基于上述考虑，本文选用FCS-MPC作为控制系统，在每个采样区间通过得到成本函数的最优解来确定开关状态，所有开关状态的数量可表示为

N=LP。

(3)

式中：L为变换器级数；P为相数。本文使用的两级三项变换器有8种开关状态如图3所示，V1到V6为正常工作状态，V7、V8为自由轮换状态。

图3 逆变器各个开关状态Fig.3 Inverter switching states

则逆变器输出电压可表示为

(4)

FCS-MPC通过每种开关状态的输出以及相关成本函数进行计算，并选择符合成本函数的最优开关状态输入至控制系统。在每个预测区间可进行多步预测，但也会极大地增加计算负担。且无论额外预测多少步数，只有第一步的结果会应用至变换器，其余的多步预测结果会被忽略，FCS-MPC的流程图如图4所示。

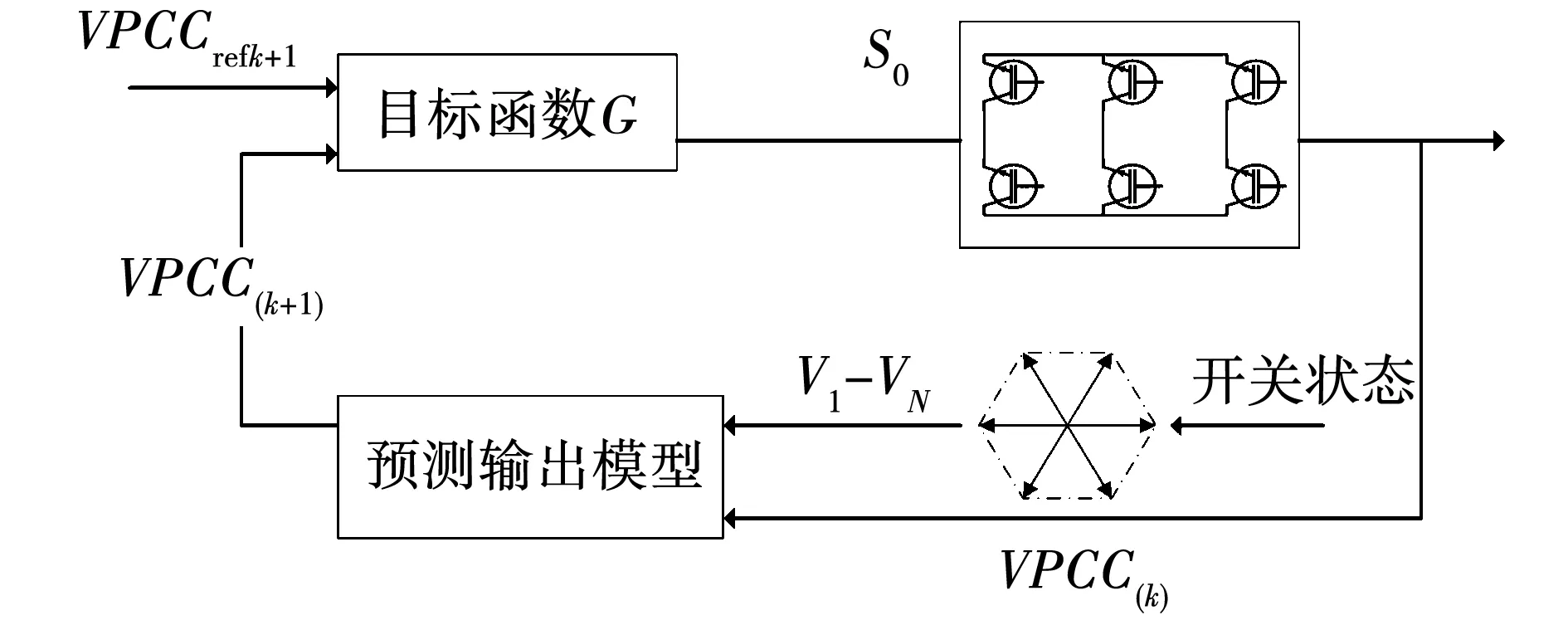
图4 FCS-MPC控制流程图Fig.4 FCS-MPC control flowchart

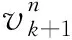
图5 FCS-MPC寻优过程Fig.5 FCS-MPC optimization process

3 基于FCS-MPC的电能质量综合调节器

3.1 串联型有源滤波器的离散数学模型

结合式(1)、式(2)即可得出变压器变比为1∶1时的时变方程为：

(5)

(6)

(7)

式中：i1(k)、i1(k+1)为当前时间与下一时刻一次绕组与二次绕组的电流；i2(k)、i2(k+1)为当前时刻与下一时刻二次绕组电流；Ts为采样时间；Lm为变压器互感；Rm为变压器阻抗；VA为PCC节点A相即时电压；A、B、C、D、E为恒定因数，可表示为：

A=Ll1+Lm+LL；

B=Ll2+Lm；

C=r1+Rm+RL；

D=r2+Rm；

式中：Ll1，Ll2为变压器漏感；LL为线路侧感抗。

3.2 成本函数与自适应权重因子的选取

设定该控制器的最终目标是使PCC节点电压、负载电流以及谐波畸变率与设定的参考值偏差达到最小，但同时考虑幅值与谐波扰动就必须设定合适的权重因子，现实配电网中情况多变，不能一直依赖人为输入或是使用刻板的查表法进行确定，本文使用归一化的方式设置了一种自适应权重因子选择的方法，解决了这一弊端。首先，设定电流、电压幅值成本函数和电压、电流谐波畸变率成本函数为：

abs[imag(VPCC(k+1)-VPCC-ref(k+1))]}+

abs[imag(IL(k+1)-IL-ref(k+1))]}；

(8)

(9)

式中：VPCC(k+1)为根据当前情况预测下一时刻公共耦合节点的电压；VPCC-ref(k+1)为下一时刻的电压参考值，根据设定的采样时间Ts不同，其数值可能并非一成不变；VPCCTHD、ILTHD为PCC节点电压、电流的谐波畸变率。

该控制方法中需要采集的变量包括变压器一次侧和二次侧的电压与电流、变压器一次侧电压电流的谐波畸变率以及一次侧的基波电压。本文提出的成本函数希望同时考虑了幅值与谐波畸变的关系，为求解上述的多目标优化问题，再将两个成本函数g1、g2聚合为单一函数，根据电压电流之间的偏差大小自适应调整两个目标之间的权重参数。对各成本函数标幺化处理后的总目标函数g可表示为：

(10)

式中：λ为根据电压、电流情况自适应取值的权重因子；λ1、λ2为人为设定的权重因数，反映两者之间的重要程度，其取值应恒为正数，本文设置的配电网对电压幅值的要求较高，因此将λ1设置为0.6，而λ2设置为0.4；g1max为最大幅值扰动偏差、g2max为谐波污染偏差，根据配电网的情况进行设定。通过使用经归一化的目标函数g即可实现根据配电网中的不同情况完成自适应治理，g取值最小的即是下一时刻最佳的开关状态，当g取值为负时，该设备工作于滤波状态，而g大于等于0时，工作在幅值扰动治理状态。

除了直接给定下一时刻的VPCCrefk+1，还有以下三种方式可以根据目前的VPCC推测下一时刻的VPCCrefk+1：

1)设定采样时间Ts较小，即可认为当前时刻与下一时刻的PPC节点电压参考值相同，即

VPCCrefk+1=VPCCrefk。

(11)

2)使用拉格朗日插值公式计算下一时刻参考电压为

VPCCrefk+1=4VPCCrefk-6VPCCrefk-1+4VPCCrefk-2。

(12)

3)通过欧拉公式与相角预测下一时刻参考电压为

VPCCrefk+1=VPCCrefkej(θ+ωTs)。

(13)

总体控制流程图如图6所示。

图6 总体控制流程图Fig.6 Control strategy flowchart

4 仿真验证

4.1 电压幅值扰动

4.1.1 三相电压幅值扰动

电压幅值扰动为主动配电网中的常见扰动形式，当风机接入配网时由于无功需求变大，在PCC节点常出现电压暂降特征，反之，风机离网时由于无功需求减小，PCC节点常伴有电压暂升特征，风机孤岛运行时也无法避免电压的幅值扰动。本文所提方法通过改变变压器二次侧电压V2进而影响i2(k+1)、i1(k+2)，最终对VPCC进行控制。设置电压幅值扰动如图7(a)所示，从0 s到0.06 s电压幅值正常，0.06 s到0.1 s电压出现暂降扰动，降幅约为20%，从0.1 s至0.15 s电压出现暂升扰动，约上升30%，0.15 s至0.2 s电压恢复正常；本次治理验证了上文提出的VPCCrefk+1公式的正确性，使用式(10)进行治理，效果如图7(b)所示，可见治理效果良好，说明该串联型有源滤波器可胜任电压幅值扰动的治理。

图7 三相电压幅值扰动及其治理Fig.7 Three-phase voltage amplitude disturbance and its improvement

4.1.2 短路故障

本次仿真案例使用串联型有源滤波器对不对称短路故障造成的扰动进行补偿，假设在源侧A相发生单相短路，PCC节点处电压波形如图8(a)所示，单相短路故障由0.07 s开始，持续全程，接入有源滤波器的电压波形如图8(b)所示,经比较后可得出，该结构可以处理由不对称短路引起的电压暂降扰动。

图8 由短路故障引起的单相电压幅值扰动及其治理Fig.8 Single-phase voltage amplitude disturbance caused by short-circuit fault and its improvement

4.2 谐波污染

主动配电网中具有大量的谐波源，如光伏发电阵列、燃料电池或是电动汽车等非线性负载，光伏系统无论是并网还是中断都会向系统内注入大量谐波，谐波污染是其主要扰动特征；串联型有源滤波器虽然具有电力电子结构，但却不会产生谐波污染，这是由于变压器一次侧对基波呈现短路阻抗，其值很小，对系统几乎没有影响，而对谐波呈高阻抗，基波的短路阻抗远小于谐波的高阻抗，因此可对谐波起隔离作用。

图9 对于基波的等效阻抗电路Fig.9 Equivalent impedance circuit for fundamental waves

(14)

(15)

(16)

有源滤波器对于基波的等效电路如图10所示。可以看出，对于基波而言，其等效阻抗为一次侧的漏电抗，其值较小。

图10 对于谐波的等效阻抗电路Fig.10 Equivalent impedance circuit for harmonics

(17)

得到等效阻抗后，则系统对于基波、谐波的等效电路如图11和图12所示。其中：Zs1为系统中的基波阻抗；Zsn为n次谐波阻抗；Zf1为无源滤波支路的基波阻抗；Zfn为无源滤波支路的n次谐波阻抗；I1为基波电流；In为谐波源产生的n次谐波电流；Z1+Z2为变压器一次侧的基波漏阻抗；nZm为串联变压器中的谐波阻抗。

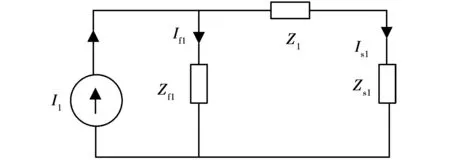
图11 系统基波等效电路Fig.11 Equivalent circuit of system fundamental currents

图12 系统谐波等效电路Fig.12 Equivalent circuit of system harmonics

在基波电路中Z1+Z2非常小，变压器接入系统的影响很小，在该电路中无源滤波器仅起无功补偿的作用，在谐波等效电路中，串联变压器的等效电阻nZm起谐波隔离的作用，最后流入的谐波电流为

(18)

由于Zsn远小于nZm，则

(19)

(20)

对于超过3次、5次的谐波，如7次谐波的等效阻抗Zf7远小于变压器的一次侧谐波等效阻抗，则可以不加装7次及以上的高通滤波器，简化了设计。因此，本文的结构可以胜任对谐波电流的抑制，且结构中的无源支路也较为简单。

4.2.1 源侧谐波扰动

为验证有源滤波器谐波方面的隔离与治理效果，在源侧设置谐波源，可模拟光伏燃料电池等分布式电源，在t=0.1 s时，向系统中注入15%的5次谐波以及10%的7次谐波，直到仿真结束，总谐波畸变率(total harmonic distortion,THD)为17.91%,如图13(a)所示；经有源滤波器隔离后的结果置于图13(b)中，可见波形已有明显改观，PCC节点总谐波畸变率亦下降至2.53%,可证明该方法的有效性。

图13 源侧谐波扰动及其隔离Fig.13 Harmonic disturbance and improvement at source-side

4.2.2 负载侧谐波扰动

本案例用于模拟负载侧出现非线性负荷如电弧炉或是电动汽车引起的谐波扰动情况，与源侧谐波扰动相似，如图14(a)所示，可从傅里叶分析中得出谐波成分约9.2%的5次谐波，约8.3%的7次谐波以及3.1%的11次谐波，总谐波畸变率为12.83%。使用有源滤波器后的波形置于图14(b)中，总谐波畸变率为2.59%。通常来讲，只要由非线性负荷产生的谐波幅值低于逆变器侧的直流电压源，频率低于控制器频率，本文所提方法即可对平衡或是非平衡的电压畸变完成补偿。

图14 负载侧谐波扰动及其隔离Fig.14 Harmonic disturbance at the load side and improvement

4.3 基于IEEE 13节点配电网的实验

4.3.1 配电网参数

本文后续实验建立在以IEEE 13节点平衡测试系统为原型的主动配电网系统基础上，如图15所示。连接到运行电压为69 kV的公共电网，配电系统运行于13.8 kV。变压器参数如表1所示，配电网负载如表2所示。该有源滤波器串联在8号变压器(Tr-8)的低压侧。模型包含两种DG，分别为光伏和燃料电池。其余负荷参数置于表2中，本系统频率为60 Hz，采样时长为0.2 s。

图15 基于IEEE 13节点主动配电网结构图Fig.15 Structure of active distribution network based on IEEE 13 nodes

表1 系统变压器配置参数

表2 系统负载配置参数

主动配电网的渗透率[20]基准为

(21)

式中：Pi,DG-non为系统内第i个分布式电源的装机容量；n为系统内分布式电源个数；PL,sum为系统内负荷总功率。本文中加入的DGs即光伏、燃料电池均通过正弦脉宽调制(sinusoidal pulse width modulation,SPWM)三相变流器并网。

4.3.2 治理效果

结合上述搭建的IEEE 13节点主动配电网验证串联型有源滤波器的治理效果，该系统中的DG包含光伏与燃料电池，DG的逆变器采用正弦脉宽调制SPWM来保证输出电压与参考电压一致，有源滤波器的直流源电压被提升至400 V，无源滤波器采用最简单的3次、5次单调滤波器，仿真时系统运行于并网状态。

系统中的总负载为9 280 kW，当只接入容量为0.3 MW的光伏设备时，实验系统的渗透率为32.3%。此时的波形如图16(a)所示，该工况下的渗透率等级较低，分布式电源对系统的影响有限，仅出现了轻微的幅值波动，谐波畸变率为5.02%,经滤波后的THD下降至1.46%,如图16(b)所示。

图16 较低渗透率等级下的扰动及其治理Fig.16 Disturbance and improvement under low permeability level

当光伏与燃料电池同时接入时，光伏接入的总容量为0.4 MW，燃料电池总容量为0.2 MW，则该实验系统中分布式电源总装机容量为0.6 MW，计算可得该实验系统中的主动配电网渗透率为64.7%，通常来讲，系统渗透率超过50%即可称其为高渗透率系统，该实验系统符合高渗透率的描述。未接入有源滤波器的DG输出波形如图17(a)所示，可见除了受逆变器影响需要滤波外，电压幅值也不够稳定，在0.02 s左右出现了较大的幅值波动，需要一定电压补偿，此时的THD为12.24%，且11次、13次等高次谐波占比较大。

接入经FCS-MPC调制的有源滤波器后的系统PCC节点电压波形如图17(b)所示，可见经治理后的波形幅值稳定，且THD仅为2.92%，良好的滤波效果来自与上文所述的可调电抗器的自身结构优势，即对谐波展现较大的励磁阻抗，而对基波展现较小的漏电抗，经过简单的无源滤波器即可完成谐波治理。仿真结果证明本文所提方法可用于高渗透率主动配电网背景下的电能质量治理。

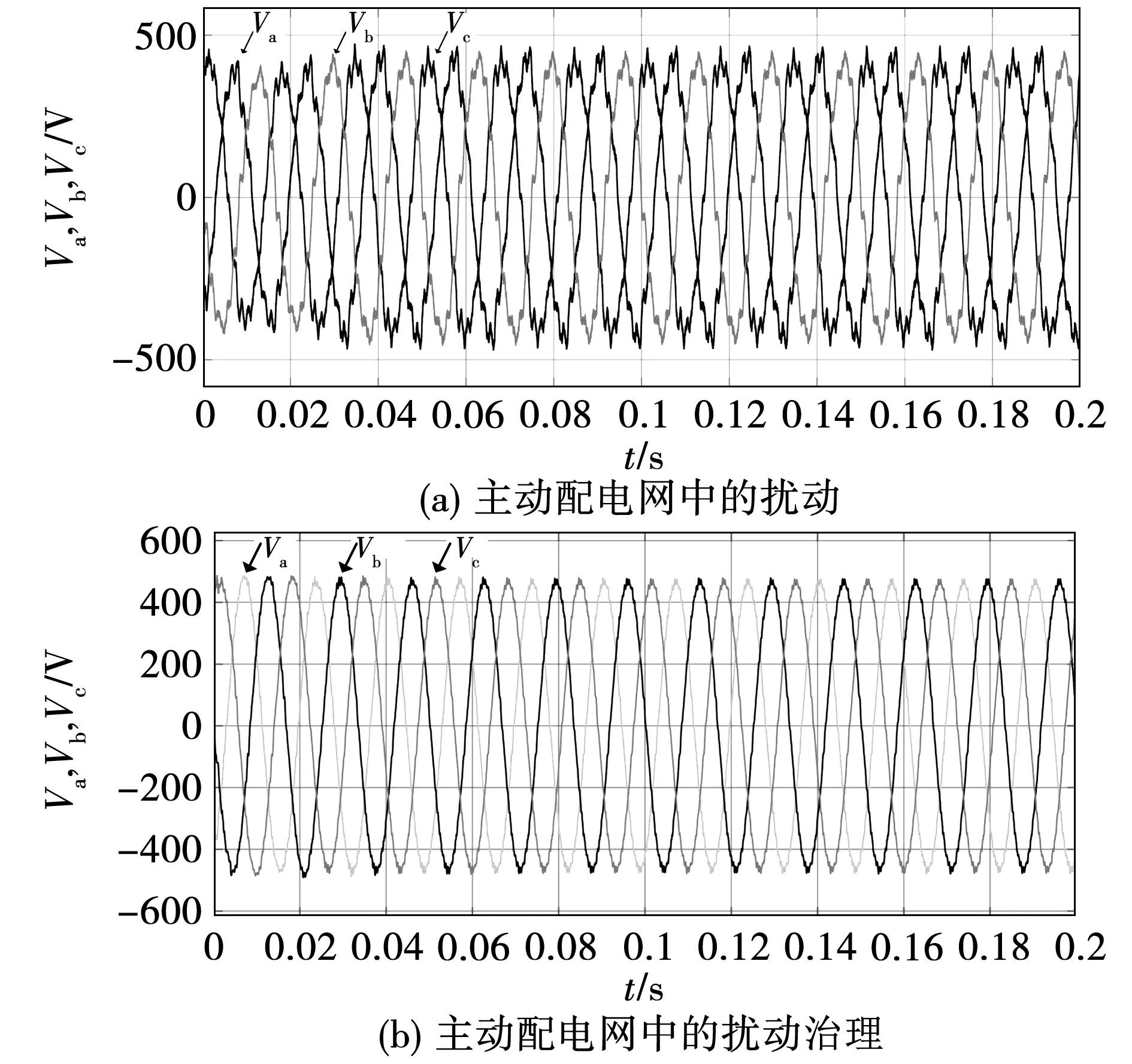
图17 较高渗透率等级下的扰动及其治理Fig.17 Disturbance and improvement under high permeability level

4.3.3 主动配电网各节点谐波分析

涉及到系统中的滤波技术，就很难忽视鼹鼠效应。鼹鼠效应是一种配电网中长距离馈线中经常出现的一种现象，其通常表现为在电能质量治理过程中如有源滤波器安装后经常造成某些母线的电压谐波含量降低，而其他母线电压谐波含量增高的情况，如需解决这个问题往往需要大量的主动滤波器接入至多个不同的节点，但在现实中这是不切实际的。而有源滤波器由于上文所述的优势，并不存在这个问题。为进一步论述主动配电网的整体谐波情况，在上述搭建的IEEE 13节点的配置下对每个节点的谐波进行分析，如图18所示。根据IEEE 3002.8-2018标准指出，正常运行系统中电压谐波畸变率应小于5%[20]，而未接入可变电抗器时，主动配电网中的3、4、5节点的THD皆超过5%，说明这种情况下有多个节点处于非正常运行状态，而接入主动电抗器后的配电网谐波情况有所好转，配电网中的所有节点皆在正常运行的范围内，说明串联型有源滤波器对谐波进行了有效的隔离，不仅仅局限于串联型有源滤波器接入的单个节点，而是在整个系统中的所有节点都有着良好的表现。

图18 主动配电网各节点谐波畸变率Fig.18 THD of each node in active distribution network

将本文的方法与已有文献进行对比，从而进一步说明本文所提方法具有的优势，如表3所示。文献[21-24]中，使用的智能阻抗(smart impedance，SI)与本文方法的结构和原理相似，但本文的控制方式与这些已有的文献并不相同，本文的阻抗可根据实际情况在感性与容性之间变化，而传统的智能电抗只能呈现感性电抗。在具有谐波源的条件下进行测试并对治理后的电压谐波畸变率进行比较，从表3可以看出，本文的控制方法更为有效，且具有一定的创新性。

表3 文献对比

5 结 论

本文依据磁通控制原理提出了一种基于串联型有源滤波器的电能质量调节器，其具有可调电抗器的特性，并可对幅值扰动、谐波污染进行综合治理。该调节器不仅结构简单、对原配电系统几乎不产生影响，还对变量检测要求较低，无需对系统中的具体谐波分量进行追踪，而是利用其谐波隔离的优势从而保障系统中的电能质量。本文将FCS-MPC算法进行了重新设计，在自适应权重选择的帮助下可以根据不同的扰动情况自行判断，选择最优开关状态，更加适合在高渗透率主动配电网中使用。为验证本文方法的有效性，搭建了包含光伏、燃料电池的IEEE 13 节点的高渗透率主动配电网，并进行了相应的结果验证，仿真结果表明，本文所提方法可以将谐波畸变率从原来的40.54%降至2.92%，且经治理后的各个节点THD均小于5%，说明该串联型有源滤波器的谐波隔离效果较佳。在与已有的文献进行比较后，结果说明该串联型有源滤波器在阻抗的调节范围以及滤波效果上都具有较大优势，再次说明了本文方法的有效性。