基于参数分析的蓄电池模型健康状态估计
2022-02-25张利国李宇剑苗广轩于东博
张利国,李宇剑,刘 乐,苗广轩,于东博
(1.东北石油大学秦皇岛校区,河北 秦皇岛 066000;2.东北石油大学物理与电子工程学院,黑龙江 大庆 163000)
0 引言
应急电源的备用蓄电池组一般由多节蓄电池经过串、并联组成,以满足一定的电压、功率以及总容量需求。当多个单体蓄电池通过串联组成蓄电池组时,模组的性能水平不再简单地由其中某个单体决定,也不等同于所有蓄电池的平均性能,而是由单体性能表现最差的多个蓄电池决定的[1-2]。蓄电池组性能快速衰减的主要原因是蓄电池组内部单体之间的不一致性,而且模组的应用会令性能相对较差的蓄电池衰变加速,从而导致单体之间的不一致性随着使用时间的增长变得越来越严重。为了确保蓄电池组在应急充放电阶段运行可靠、降低蓄电池的全生命周期成本,须保证在蓄电池组的应急放电之前及时、准确地了解蓄电池组各节蓄电池的健康状态并采取进一步措施,以提高蓄电池组的利用率。
基于模型法估计单体蓄电池健康状态[3-6]是目前主流的健康状态(state of health,SOH)估计方法。该方法通过选取合适的蓄电池等效电路模型作为研究蓄电池的老化模型,利用诸如最小二乘法、卡尔曼滤波算法等智能算法实现蓄电池模型参数的在线辨识[7-11],从而建立电路模型参数与SOH的关系[12-13],进而实现蓄电池健康状态的实时估计。即,在荷电状态相同的条件下,基于模型法的蓄电池SOH估计主要通过改进蓄电池等效模型以及模型参数的辨识方法来提高蓄电池SOH的估计精度。另一种比较流行的基于特征法的SOH估计方法,即利用蓄电池老化过程中所表现出来特征量的变化,从而建立健康状态与蓄电池特征量关系。文献[14]介绍了一种基于蓄电池微分容量(differential capacity,DC)或微分电压(differential voltage,DV)特性的SOH估算方法。但是该类方法易受到充放电制度以及初始情况的影响,分析结果会存在诸多不确定因素。Gregory L.Plett等通过扩展卡尔曼滤波(extended kalman filter,EKF)算法来测量蓄电池的内阻,以及电量的变化与蓄电池SOH之间的关系,进而估算蓄电池的SOH[15]。
为了保证蓄电池在应急放电时刻的输出性能,及时、准确地评价蓄电池的老化程度,本文以蓄电池定期维护放电阶段获得的SOH值作为应急放电周期的SOH值。因此,本文是在蓄电池组定期维护放电阶段的背景下,实现蓄电池组中单节蓄电池健康状态的估计。所谓定期维护放电阶段,即每次定期维护放电的形式均为恒流放电(放固定容量)→恒流结合恒压充电→浮充,且每次恒流放电容量均是额定容量的20%。当蓄电池组每次维护放出固定容量(额定容量的20%)后,单节蓄电池模型参数会随着蓄电池健康状态以及荷电状态而变化。虽然基于模型法估计SOH有一定效果,但是其并没有从因果关系上分析荷电状态对于模型参数的影响,而是直接建立模型参数和SOH的关系。这样就难以得到不同工况下最适合的SOH评价方法。
本文根据铅酸蓄电池的化学原理并考虑到等效模型在工程中实现的便利性,选取二阶RC电路模型,采用端电压比较法验证所选电路模型的合理性以及辨识参数的准确性。然后对同一型号铅酸蓄电池进行老化试验,通过分析蓄电池模型参数与维护放电后的荷电状态(state of charge,SOC)以及SOH的关系,建立蓄电池定期放电维护(额定容量的20%)后的欧姆内阻R0与SOH的关系,从而实现蓄电池SOH的估计。通过试验验证可知,采用本文方法预测铅酸蓄电池健康状态与采用定义法获取的实际蓄电池健康状态的相对误差在3%左右。这表明本文方法可以很好地实现蓄电池健康状态估计。
1 蓄电池等效模型的选取
根据建模依据的不同,对蓄电池进行健康状态估计的蓄电池模型可分为电化学模型、数学模型以及等效电路模型三种[16-19]。常用的等效电路模型[20]包括Rint模型、Thevenin模型、新一代汽车合作伙伴(partnership for new generation of vehicles,PNGV)模型以及Massimo Cerado模型等。在实际应用中,建立等效电路模型不仅要考虑模型的精确度,而且要兼顾其复杂性等诸多要求。
本文选择标称电压为6 V、标称容量为5 A的某品牌铅酸蓄电池,在SOC为0.80(以0.3C脉冲电流放电5%SOC)状态下实测放电结束后端电压响应曲线。利用MATLAB中的cftool工具箱,对放电结束后的这段曲线进行单指数、双指数以及三指数拟合。指数项拟合曲线如图1所示。

图1 指数项拟合曲线
由图1可以看出,双指数和三指数拟合效果均优于单指数拟合效果,说明双指数以及三指数曲线拟合度较单指数拟合度高。因此,双指数以及三指数拟合更能精确反映蓄电池的极化效应。根据上述对于等效电路模型选取的要求可知,本文选取二阶RC模型作为蓄电池的等效电路模型。二阶RC等效电路模型如图2所示。
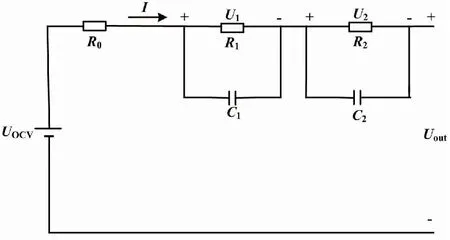
图2 二阶RC等效电路模型
图2中:UOCV为蓄电池的开路电压,用于描述正负极稳定的电位差;R0为欧姆内阻;R1、C1、R2、C2用于描述蓄电池极化的动态特性;电压Uout为有负载时的端电压。此外,本文规定流经欧姆内阻R0的电流I在放电时为正、充电时为负。
2 脉冲放电法实现蓄电池等效模型的参数辨识
为了实现蓄电池模型的参数化,以便通过可测量数据的运算得到蓄电池相关状态信息,本文利用蓄电池恒流脉冲放电试验结合MATLAB曲线拟合的方式,获取蓄电池等效电路模型中的各参量值。脉冲放电试验流程如图3所示。
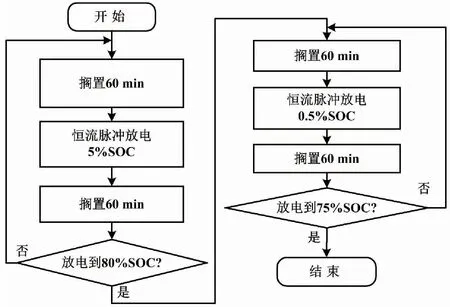
图3 脉冲放电试验流程
本文试验所采用脉冲放电电流幅度为0.3 C,使用电子负载EBC-A10H对蓄电池的特定SOC区间(75%~100%)进行脉冲放电试验测试。当SOC区间为80%~100%时,每隔5%SOC进行一次脉冲放电并采集数据。当SOC为80%以下时,每隔0.5%SOC进行一次脉冲放电,直至SOC为75%为止。
2.1 蓄电池模型参数辨识
本文选取2阶RC电路模型作为蓄电池的等效电路模型。根据等效电路模型得到的函数关系式如式(1)所示。
(1)
选取经脉冲放电后荷电状态SOC为80%时的曲线(B-C-D段)为研究对象。端电压、电流变化曲线如图4所示。

图4 端电压、电流变化曲线
根据图4所示,由A点开始恒流脉冲放电一段时间至B点;当脉冲电流瞬间为零,蓄电池端电压瞬间上升至C点;剩余时间处于搁置状态直至D点。根据脉冲电流突变为0 A时的蓄电池端电压瞬变量,即图4所示的B-C段,利用式(2)可以求得欧姆内阻R0。其中:I为恒流放电截止前的电流。
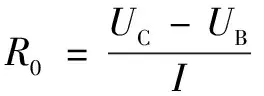
(2)
令tb、t0、tr分别为放电开始时刻、放电停止时刻和静置停止时刻。在此过程中可得到RC网路电压,如式(3)和式(4)所示。
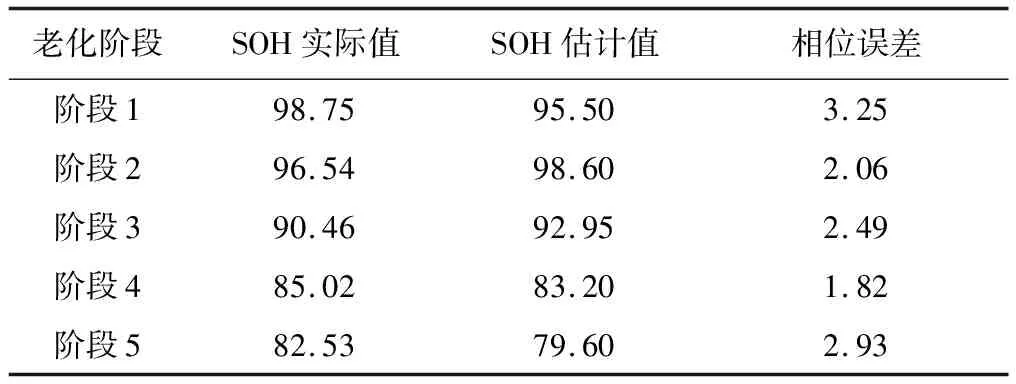
当t0 (3) 当tb (4) 式中:τ1=R1C1;τ2=R2C2。 τ1和τ2反映了蓄电池在不同工作状态下恢复到稳态的时间。 当t0 在tb (5) 由以上分析可知,通过恒流脉冲放电后蓄电池端电压的变化曲线,结合曲线拟合方法,就可以辨识出二阶RC等效电路模型在不同荷电状态下的模型参数。 本节采用端电压比较法验证二阶RC模型的合理性和参数辨识的准确性。蓄电池模型的搭建采用MATLAB_Simulink中simscape的诸多模块构成。本文选用了基于蓄电池等效电路串并联关系的物理组件进行建模,通过将辨识得到的各模型参数与SOC的关系,利用Lookup Table实现模型中电阻、电容等参数的实时获取。由于是参数验证阶段而非实际工程使用,本节采用较为简单的安时积分法实现SOC的估计,并结合SOC-OCV得到OCV估计值。因为本文主要是针对备用电源蓄电池维护放电阶段而言的,故验证试验采用恒流放电试验。蓄电池的仿真验证模型如图5所示。 图5 蓄电池的仿真验证模型 在室温下,将0.3 C电流作为蓄电池模型的输入量,记录蓄电池恒流放电至SOC为75%左右的放电数据,通过上述验证模型得出端电压的估计值,并与实测值进行对比。 蓄电池输出端电压如图6所示。由图6可知,电压实测值和电压估计值的差值ΔU均在10 mV以内。在部分放电时间内,电压估计值没有很好地跟随实测值。这是由于在试验数据不充分的情况下,数据查表过程中必定会引入误差。故该蓄电池模型参数基本可以满足蓄电池恒流放电试验的模型参数精度要求。 图6 蓄电池输出端电压 在实际使用过程中,不确定的老化因素以及不同的特征会直接影响蓄电池老化的速率,形成不一样的老化途径[21]。在蓄电池成组后,单节蓄电池之间的不一致性会越来越严重。为了能较好地保证蓄电池组的输出性能、及时了解单节蓄电池的性能,本文利用蓄电池组定期维护放电阶段,实现蓄电池组中单节蓄电池在寿命周期内的SOH估算。 SOH的定义是:相同放电条件下,蓄电池当前容量和起始健康状态容量的比值[22-24]。其取值SSOH如式(6)所示。 (6) 式中:分子C(T,Ia,KSOH)是蓄电池处于某一健康状态KSOH和温度T下,以负载电流Ia从满充放电至终止电压所能释放的容量,且SOH取值为小于等于1的正数。 因为应急电源铅酸蓄电池组常年处于室温条件下工作,所以本文不考虑温度变化对研究蓄电池健康状态的影响。 由于本文正是利用备用蓄电池组在定期维护放电阶段来实现蓄电池组单节蓄电池的健康状态估计,所以本文在室温下,对DJW6-5.0(6 V、5 A)理士牌铅酸蓄电池进行蓄电池模型参数与健康状态关系的研究。具体的老化试验流程如下。 ①首先,利用蓄电池充放电设备EBC-A10H,在室温(23±3)℃条件下对蓄电池进行0.3 C放电电流的放电容量测试,且在该放电电流下的容量至少需测量三次,取均值保证该电流下蓄电池容量测量的准确性。然后,采用先恒流(1.5 A)再恒压(7.2 V)的方式对蓄电池进行充电。最后,进行该放电容量下的等SOC恒流脉冲电流放电测试试验,得到该放电容量下的模型参数随SOC的变化趋势。 ②将三节铅酸蓄电池串联成蓄电池组置于浮充阶段一个月,即室温条件下,单节蓄电池(6 V、5 A)的浮充电压设置为6.9 V。然后对该蓄电池采取步骤①的试验内容,即在室温条件下进行放电电流为0.3 C的放电容量测试以及恒流脉冲放电测试试验。 ③重复步骤①和步骤②,直至利用式(6)定义法获取的蓄电池健康状态接近于80%。 通过上述老化步骤的设计,从中随机挑选一节蓄电池的老化数据,从而得到不同健康状态下二阶RC模型的模型参数R0、极化内阻随SOC的变化趋势,分别如图7、图8所示。 图7 R0随SOC的变化趋势 图8 极化内阻随SOC的变化趋势 根据图7可以得出如下结论:①当蓄电池处于某健康状态下,R0随着SOC的变化较小,R0的具体变化范围大概在2 mΩ左右,故可以忽略SOC变化对于R0的影响;②当蓄电池SOC处于75%~80%之间时,R0值会随着蓄电池健康状态的下降而呈现上移趋势。 由图8可以得出以下结论:当蓄电池处于某健康状态下,在蓄电池SOC位于75%~80%之间时,极化内阻R1和R2随着SOC的波动较大,变化范围接近于25 mΩ。这说明在SOC处于75%~80%之间时,极化内阻随着SOC的变化而呈现较为剧烈的抖动。 本文是在备用蓄电池组处于定期维护放电阶段实现蓄电池健康状态的研究。所谓定期维护放电(即每次定期维护放电)的形式均是恒流放出固定容量-恒流限压结合恒压充电-浮充,且每次恒流放电容量均是蓄电池额定容量的20%左右。由图7可知,当蓄电池SOC处于75%~80%之间时,可忽略SOC变化对于蓄电池欧姆内阻R0的影响,且欧姆内阻R0会随着蓄电池健康状态的下降呈现增加趋势。于是,经整理蓄电池老化试验结果可知,当蓄电池健康状态从100%降低到80%左右、其维护放电(额定容量的20%)后SOC值处于75%~80%之间时,欧姆内阻R0会随着蓄电池健康状态的下降呈现增加的趋势。蓄电池欧姆内阻R0随SOH值的变化趋势如图9所示。 图9 R0随SOH值的变化趋势 根据图9可知,在蓄电池健康状态处于80%以上时,蓄电池欧姆内阻R0会随着蓄电池健康状态的下降而增加,且R0的变化与蓄电池SOH值的变化呈现近似线性关系。故可以在蓄电池恒流放电维护后(即蓄电池放出蓄电池额定容量的20%后),通过蓄电池模型参数辨识得到欧姆内阻R0,从而实现蓄电池健康状态定量估计。 为了更好地得到蓄电池欧姆内阻R0与SOH的关系,本文利用傅里叶展开式进行拟合。拟合关系式如式(7)所示。 f(x)=a0+a1cos(ω×x)+a2sin(ω×x) (7) 图10所示为SOH关于R0的关系拟合曲线。 图10 R0与SOH值关系的拟合曲线 由图10可以看出,傅里叶展开式拟合效果较好。利用R0得到了SOH的预测模型,如式(8)所示。拟合度R-square为0.958 9。 SSOH=0.904+0.002cos(0.912r0)- 0.098 2sin(0.912r0) (8) 利用该方法对理士牌铅酸蓄电池进行单体蓄电池的健康状态估计,其标称电压为6 V、标称容量为5 A。具体试验验证流程如下。 ①获取新蓄电池在0.3 C电流下的实际放电容量。 ②将蓄电池浮充一段时间后,对下一老化阶段,利用蓄电池充放电设备EBC-A10H,在室温(23±3)℃条件下获取放电电流I为0.3 C的蓄电池放电容量。 ③在步骤②放电容量下,利用蓄电池放出固定容量后辨识得到欧姆内阻R0,并通过R0与SOH的对应关系得到该状态下的SOH的估计值。 ④重复步骤②和步骤③,直至SOH值接近80%为止。 根据以上试验验证流程,由定义法获取SOH值和蓄电池SOH估计值的对比数据。蓄电池SOH估计误差如表1所示。 表1 蓄电池SOH估计误差 因SOH取值在0~1之间,于是本文采用百分比的形式表示蓄电池的SOH值。由表1可知,SOH实际值是利用每个老化阶段的蓄电池实际放电容量,采用SOH的定义直接获取。由此可以看出,采用本文方法预测铅酸蓄电池健康状态与采用定义法获取的健康状态的相对误差在3%左右,说明该方法可以很好地用于单体蓄电池健康状态估计,为实现蓄电池组的有效利用奠定基础。 本文在蓄电池模型参数辨识的基础上,通过分析模型参数与维护放出固定容量后的SOC值以及SOH值的关系,建立蓄电池定期放电维护(额定容量的20%)后欧姆内阻R0与SOH的关系,以实现蓄电池健康状态的估计,从而及时发现单体蓄电池问题,提高蓄电池组使用寿命。通过对蓄电池的老化试验,可以得到以下结论。 ①蓄电池健康状态衰减至80%之前,其维护放出固定容量(额定容量的20%)后SOC处于80%到75%之间时,SOC的变化对于R0的影响可忽略;同时,当蓄电池健康状态在80%以上、维护放出固定容量后SOC处于80%到75%之间时,欧姆内阻R0随着健康状态的下降呈现上移趋势,为定量估计SOH值奠定理论基础。 ②通过分析蓄电池模型参数与蓄电池维护后SOC值以及SOH值的关系,建立蓄电池维护放出固定容量(额定容量的20%)后的R0值与蓄电池当前SOH值的对应关系,为蓄电池SOH的准确估计提供支撑。 ③本文在蓄电池模型参数辨识部分采用离线恒流脉冲放电法,为在线、低成本的模型辨识算法创造了条件,也为更好地实现蓄电池健康状态的定性和定量分析奠定了基础。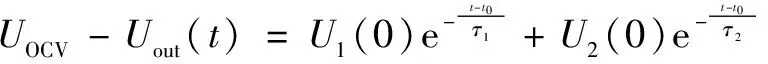

2.2 模型参数辨识精度验证
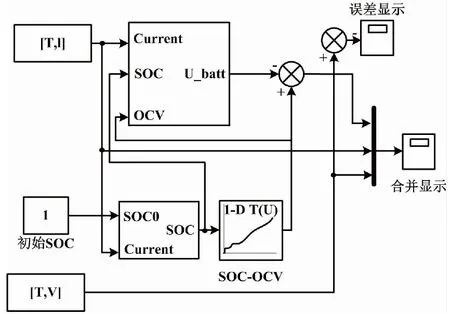

3 单体蓄电池健康状态估计
3.1 蓄电池模型参数特性分析
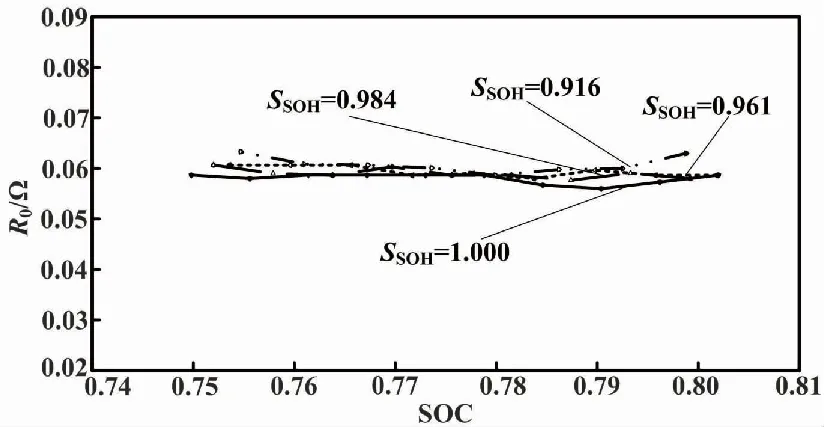
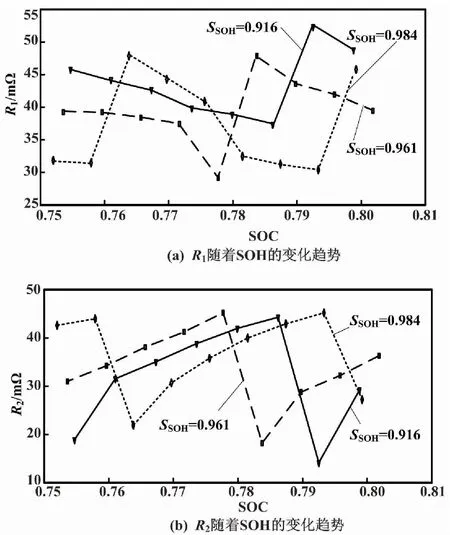
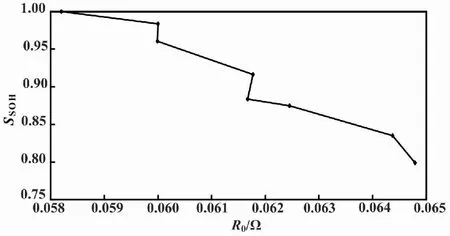
3.2 基于模型参数估计蓄电池SOH值

3.3 试验结果与分析
4 结论
