基于EAM的控制分配设计策略在控制律设计中的应用

曲小宇，李 涛

(1.中国商飞上海飞机设计研究院，上海 201210；2.民用飞机模拟飞行国家重点实验室，上海 201210)

0 引言

随着现代飞机电传飞控技术的发展，多操纵面气动布局设计已广泛应用于先进飞机的总体设计。该设计一方面可提高飞机的设计性能，另一方面可提高飞机的使用效率。通过不断地更新发动机和机载设备，可使气动布局良好的飞机使用期限延长几十年，从而极大地降低飞机研制费用、缩短研制周期[1-8]。

飞行控制律是现代先进飞机电传飞控系统的核心。针对先进飞机的飞行控制律，无论是基于线性飞机还是非线性飞机的假设，都是围绕如何对操纵面进行合理控制而设计的。传统控制策略直接计算给作动器的指令控制。例如，特征结构配置法(eigenstructure assignment method,EAM)不仅能配置闭环系统的极点，还能配置特征向量，使被控系统的动态响应在满足一定阻尼特性的同时，又能保持各模态之间达到期望的关联/解耦合特性，达到了良好的控制效果[9]。随着现代控制理论的不断发展，基于电传飞控系统的先进飞机越来越多地采用多操纵面气动布局设计。其优点是可提供更灵活、可靠、有效的多余度实现方式。但是，对于飞行控制律设计，不断增加的控制变量已超过了飞行员的可操纵量，采用EAM等传统方法越来越难以作出有根据的零点、极点配置选择，使直接针对操纵面设计飞行控制律的方式变得非常困难甚至无法实现。因此，如何解决多操纵面的协调分配与综合控制，已成为先进飞机飞行控制律设计中面临的首要问题。

针对多操纵面飞机的飞行控制律设计，本文提出了一种基于EAM的控制分配设计策略。该策略采用模块化[5]设计思路，使控制器分为传统控制律和控制分配两部分，并分别进行设计。首先，设计常规意义下实现指令跟踪、稳定、抗干扰等功能的传统控制律，得到三轴的虚拟控制指令。然后，完成虚拟控制指令到操纵面指令的控制分配设计。这样就可以充分利用操纵面之间内在的气动余度，通过合理地分配多操纵面，使飞机的飞行性能和飞行任务效率大幅度提高[1-8]。最后，以某型多操纵面飞机为例，采用本文提出的设计方法进行飞行控制律设计，由仿真结果验证了该设计方法的有效性。

1 特征结构配置

对于线性定常系统，有：

(1)

式中：x为状态变量,x∈Rn;y为输出变量,y∈Rp；u为输入变量,u∈Rm；A为状态矩阵,A∈Rn×n;B为输入矩阵,B∈Rn×m,rank(B)=m≠0、m>1；C为输出距阵,C∈Rr×n,rank(C)=p≠0。

输出反馈控制原理[9-10]如图1所示。

图1 输出反馈控制原理图

由图1可得输出反馈控制律：

u=Ky=KCx

(2)

则闭环系统变换为：

(3)

式中：G∈Rn×n；K∈Rm×r；x∈Rn×1；y∈Rr×n。

设G具有r个互异特征值λi(i=1,2,…,r)，对应的特征向量为vi(i=1,2,…,r)，则有：

Gvi=λivi

(4)

由文献[10]可知，给定式(1)所描述的可控可观测系统，并且设矩阵B、C均满秩，那么通过输出增益反馈即控制律u=Ky，可精确配置max(m,r)个闭环特征值。

2 控制分配

2.1 问题描述

设飞机期望的转矩向量是v(t)∈Rk，称为虚拟控制。实际操纵面的偏转向量u(t)∈Rm(m>k)，控制分配就是在给定v(t)及映射关系G：Rm→Rk的情况下，求解方程：

Gu(t)=v(t)

(5)

式中：G为控制效率矩阵,G∈Rk×m。

考虑作动器位置饱和限制和速率饱和限制，带约束的标准线性控制分配问题可以表述为[8-11]：

(6)

即在期望的输入作用下，需要求解实际操纵面的偏转向量，并满足约束条件。

2.2 目标函数

由于待分配系统的控制量维数大于目标维数，存在冗余，可将其转化为数学问题进行求解。现有控制分配算法的分配目标主要包括直接分配目标、误差最小目标、控制最小目标和混合最小目标[8]。

①直接分配目标。

通过给定控制效率矩阵G和期望转矩向量md，寻找控制向量u及标量λ。使λ取得最大值，即：

maxJ=λs.t.umin≤u≤umax

(7)

②误差最小目标。

现有控制分配所研究的最优问题，一般指限定范围内的最小分配误差问题或加权最小误差问题。其目的是求得与目标值最接近的分配结果，即：

minJ=(yd-Gu)TW(yd-Gu)s.t.umin≤u≤umax

(8)

式中:W为加权矩阵。

③控制最小目标。

仅满足分配误差最小不能充分发挥整个系统的潜力。由于存在冗余，满足最小误差的解往往不是唯一的。因此，本文在误差最小化的基础上又提出了控制最小化问题的研究，即：

(9)

④混合优化目标。

混合最优问题将误差最小和控制最小问题以线性加权的形式进行综合表述，如式(10)所示。其中:λ′表征对两个最小指标的倾向，根据具体情况选择。

(10)

混合最优方法已考虑到多个目标的优化，但是受计算量的影响，很难用于实时计算。因此，现有的分配方法主要针对分配误差，不能在此基础上进一步优化。

控制分配求解的目标往往和飞行任务有关。例如：巡航时，期望舵面阻力更小；常规飞行时，从延长寿命的角度期望舵面有较小的运动幅度。针对不同任务，可选用相应的指标来实现有针对性的优化。

2.3 优化的控制分配

针对上述四类控制分配问题的求解，结合实际的飞行控制要求，演化出了不同的控制分配研究方法。具体可以归纳为基于优化的分配法和非优化的分配法这两大类[2]。

利用优化的数学思想对控制分配问题的研究，通常基于这样一种理解：对于一个给定的虚拟控制量v，找到一个可行解u，使Gu=v。如果问题存在多个解，则选择最优解；如果问题无解，则选择使Gu最接近于v的解。为了找到符合问题的最优解，基于优化的控制分配法需要将问题的求解分为两个阶段：

(11)

(12)

式中：ud为期望的控制输入；Wu、Wv为加权矩阵。

3 基于EAM控制分配的控制律设计

模块化的设计方法使控制分配技术具有以下优点。①便于控制器中的参数调整。②便于控制器的重构设计。③简化了控制律的设计：可以仍然按传统的控制律设计虚拟控制，然后再经过分配律协调分配到相应操纵面上。④可以利用控制分配直接对操纵面进行约束限制。

控制器采用模块化策略，使控制律和分配律分开设计。首先，传感器将测量到的信号传输给控制律模块，通过设计常规意义下的控制律，完成指令跟踪、稳定、抗干扰等动作，得到三轴的虚拟控制指令。然后，将虚拟控制指令传输到控制分配模块，通过设计优化的分配逻辑，最终输出操纵面偏转指令。本文采用EAM设计传统控制律，以加权伪逆法进行控制分配设计。

基于模块化的多操纵面飞行控制原理如图2所示。

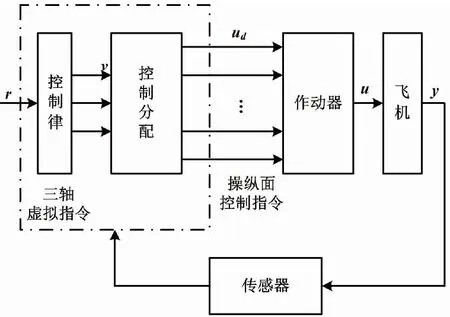
图2 基于模块化的多操纵面飞行控制原理图

3.1 控制律设计

首先，对控制器进行传统控制律的设计，采用输出反馈形式u=Ky。对于式(1)所示的闭环系统，将输入矩阵B变换为以下形式[12]：

(13)

取T=[BP]。P为使得rank(T)=n的任意矩阵。经相似变换，可得:

(14)

线性变换前后，系统的特征值不变，特征向量变为：

(15)

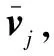
(16)

由式(16)可得闭环特征值。特征向量方程为：

(17)

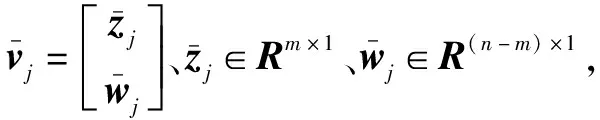
(18)

(19)

由此可求得反馈增益矩阵，为：

(20)

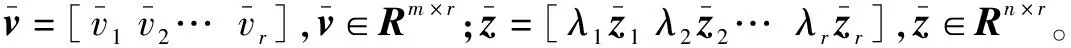
3.2 控制分配设计

对于如式(11)、式(12)所示的基于优化的控制分配问题，如果选择基于L2范数最小，则可以简化为如下形式：

(21)

对于如式(21)所示的控制分配问题，其解的形式为：

u=Fud+Nv

(22)

证明：

定义以下标量函数。

H(u,λ)=0.5(u-ud)TWu(u-ud)+λT(Gu-v)

(23)

对H分别求u和λ的偏导数，利用求极值的条件，可得：

(24)

(25)

由式(24)可得：

(26)

将式(26)代入式(25)，可得：

(27)

将式(27)代入式(26)，最终可得：

(28)

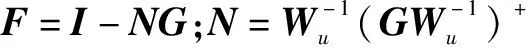
证毕。

如果取期望的控制输入ud=0，则Wu≠I时，优化指标变为：

(29)

此时可以求得其解，为：

(30)

对于加权矩阵Wu，矩阵元素的选择与操纵面控制效率有关。所以通常选取的权值矩阵为对角正定矩阵，并以操纵面位置极限值平方作为对应对角元素。如果适当增加控制效率低的操纵面的权值，则可以加大其出舵量，从而避免操纵效率高的舵面过早进入饱和状态。

3.3 基于EAM控制分配的控制律设计

基于EAM控制分配的控制器结构如图3所示。

图3 基于EAM控制分配的控制器结构图

根据式(2)和图3可以得出，传统的控制律输出v为：

v=Krr-Kx

(31)

综上所述，基于EAM控制分配的控制律设计设计步骤如下。

①根据期望实现的飞行控制系统的性能指标，对多操纵面飞行控制系统配置期望特征值。

②根据3.1节特征向量的解耦设计方法，设计期望特征向量，并计算特征向量矩阵。

③根据式(20)计算反馈增益矩阵K。

④根据式(31),可求得虚拟控制v=Krr-Kx。

⑤确定进行控制分配的目标函数。

⑥设定约束条件。

⑦选定加权矩阵Wu。

4 仿真验证

以某型多操纵面先进飞机为例进行仿真验证。其线性定常数学模型如式(1)所示。状态变量x=[αβpqr]，其模态分别为迎角、侧滑角、滚转角速率、俯仰角速率和偏航角速率。操纵面指令u=[δclδcrδelδerδr]T。其中：δcl为左鸭翼；δcr为右鸭翼；δel为左升降副翼；δer为右升降副翼；δr为方向舵。取飞行状态点M=0.22、H=3 000 m，则操纵面的位置限制如表1所示。本文的计算忽略作动器速率限制。

表1 操纵面的位置限制

控制效率矩阵为：

(32)

期望飞机运动的主导特征值为：

(33)

根据EAM，设置期望特征向量Vd。

(34)

式中：×为特征向量中不受约束的元素；0为希望解耦的元素。

短周期模态中，期望特征向量与β、p和r保持解耦，故设置对应元素为0，从而体现α和q的性能。荷兰滚运动主要与β和r有关，希望与α、q模态和p模态保持解耦，故设置对应元素为0。滚转运动则期望与α、q模态和β、r模态保持解耦，故对应元素设置为0。

当系统模型为输出反馈时，根据式(20)，求得输出反馈增益：

(35)

此时，可以精确地配置到期望的主导极点：

(36)

取Kr=K-G-1A，根据式(31)，可得虚拟控制输入:

v(t)=(K-G-1A)r-Kx

(37)

在所有飞行条件下，对于要求的控制力矩，按照使用侧重点的不同，对各个控制量进行加权，以减少气动舵面总的偏转量。本文取加权矩阵：

(38)

取仿真时间为15 s，计算方式设置为定步长，采样频率为160 Hz。

杆指令信号如图4所示。

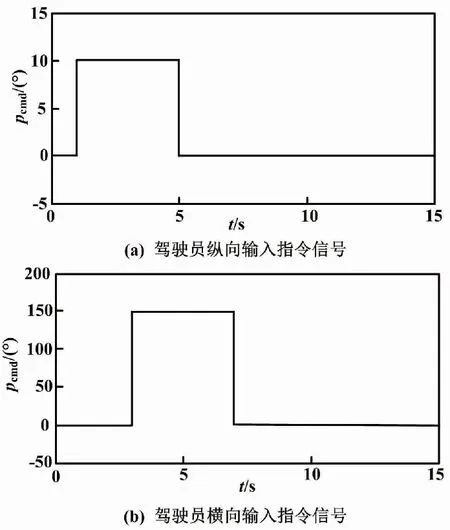
图4 杆指令信号

当t=1 s时，输入一个俯仰指令；当t=3 s，输入一个滚转的指令。

状态量响应曲线如图5所示。

图5 状态量响应曲线

从图5可以看出，采用本文提出的设计方法，可以快速、准确地响应指令，显示出了良好的控制效果。而采用传统EAM，俯仰方向的响应最大为13.9°，已大大超出指令信号，不能很好地跟踪指令。另外，操纵面的指令也已经超出了位置限制。对于多操纵面控制系统，该方法的控制效果不佳。

各操纵面的偏转情况如图6所示。其中，虚线表示物理位置限制，即上下限。

图6 各操纵面的偏转情况示意图

由图6可以看出，当t=1 s时，输入俯仰指令后，各操纵面未发生饱和。这时，两种设计方法均可以合理分配操纵面，产生相同的控制效果。但是，当t=3 s时，输入滚转指令后，传统的EAM使左、右升降舵补助翼和方向舵都超出了位置约束限制，造成了俯仰方向不能准确跟踪指令的结果。而采用基于EAM的控制分配设计方法，当右升降舵补助翼饱和时，控制分配器重新分配左升降舵补助翼和鸭翼，弥补了控制效率的不足，控制响应依然可以较好地满足期望的要求。

本文采用基于EAM的控制分配设计方法，针对多操纵面飞机，仍然按原来三轴方向对EAM进行设计，简化了计算过程。模块化后通过控制分配，只需根据式(30)进行响应的迭代运算来求解，计算速度快。进行多次MATLAB仿真计算，迭代次数取N=200，优化计算的平均时间为6.3 ms，最大时间为6.68 ms,平均误差为3.35×10-2ms，最大误差为3.78×10-2ms。仿真结果表明，该方法很好地满足了飞行控制系统的实时性要求。

由此可以看出，针对多操纵面飞机的控制律设计，传统EAM显得力不从心，而应用基于EAM的控制分配法设计的控制律能够较好地解决多操纵面的协调分配问题，保证了各个操纵面均工作在位置饱和约束范围内。整个控制系统能快速、准确地跟踪操控指令，取得了满意的控制效果。

5 结论

针对传统EAM设计多操纵面飞机存在的问题，本文基于某典型多操纵面飞机，首次研究了基于EAM和加权广义逆控制分配的多操纵面飞行控制律设计。仿真结果表明，与传统EAM设计相比，本文提出的基于EAM控制分配的控制策略既兼顾了EAM的优点，又充分利用了控制分配技术的特点，能够很好地协调分配各操纵面，发挥了冗余操纵面的潜力。该策略实际运算快速，控制效果良好，适合工程应用，为解决多操纵面飞机的飞行控制律设计拓宽了研究思路。