重型燃气轮机IGV系统建模与故障仿真

张文广，陆 瑶，王维建，尹德斌，马艳华

(1.华北电力大学控制与计算机工程学院，北京 102206；2.上海新华控制技术集团科技有限公司，上海 270062；3.上海工业自动化仪表研究院有限公司，上海 200233；4.大连理工大学微电子学院，辽宁 大连 116024)

0 引言

重型燃气轮机是能源高效转换与清洁利用系统的核心动力装备。其控制系统部件繁多，信号转换关系复杂，处于温度高、压力大等恶劣环境，现场部件在长时间运行后易发生疲劳、磨损等故障[1]。压气机作为燃气轮机的关键部位，具有很强的非线性，其性能好坏直接影响燃气轮机运行效率。进口导叶(inlet guide vane，IGV)作为压气机入口的静止叶片，通过驱动机构改变其角度来控制进入燃气轮机的空气量。IGV系统一旦发生故障，往往易导致燃气轮机停机，会造成人员和经济损失。

国内外围绕IGV系统作了大量研究工作。孙益科[2]揭示了IGV系统在机组不同运行工况中的运行规律，通过控制IGV系统提高机组运行的安全性。邢志伟[3]等假设IGV角度与作动筒位移成比例关系，建立了IGV系统模型，实现IGV角度调节。闫桂山[4]等提出伺服电机-定量泵-液压缸容积控制方案，建立泵控IGV模型，实现IGV位置控制。A.Mehrpanahi[5]等对燃气轮机系统建模，得到不同工况下最佳IGV角度，以提高热电厂效率。以上文献的研究重点主要是对IGV系统的有效控制，未涉及故障建模；在IGV系统建模中，设定IGV角度与液压缸位移成线性比例关系，并未分析机械组件间的非线性动力学关系。

目前，IGV系统的仿真建模研究较多，很少涉及IGV故障建模。因此，研究IGV系统建模与故障仿真具有重要意义。首先，对IGV系统进行机理分析，建立了IGV系统液压驱动部分和机械传动部分的动力学模型。然后，采用模块化建模方法建立IGV系统的Simulink仿真模型，通过分析液压缸内部泄漏、导叶断裂和IGV连杆松动这三种典型故障的机理，建立了IGV系统故障模型。最后，将正常工况下的模型输出结果与燃机电厂IGV历史运行数据进行了对比分析。

1 IGV系统

IGV系统结构如图1所示。

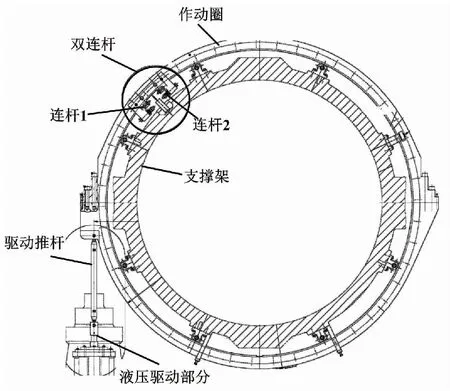
图1 IGV系统结构图

IGV是燃气轮机压气机入口一系列角度可调的静止叶片。IGV系统可以根据压气机的实际转速，通过改变导叶角度来调节压气机的进气量和进气方向，并限制启机过程中的空气流量，从而降低机组的启动功率、防止压气机喘振，对燃气轮机安全运行起着重要作用。

本文以双连杆型IGV系统为研究对象。IGV机械传动部分由作动圈、双连杆、支撑架、导叶等组成，利用双连杆与作动圈之间的相互作用进行传动。IGV驱动方式为液压驱动，由油箱、齿轮液压泵、动压反馈伺服阀、液压缸组成，即利用液压缸来推动作动圈旋转。

2 IGV系统机理建模

IGV系统由液压驱动和机械传动两大部分组成。IGV系统工作原理如图2所示。

图2 IGV系统工作原理方框图

齿轮液压泵从油箱中吸入油液，将机械能转化为液体的压力能，从而改变齿轮泵的转动角度、增大齿轮液压泵进入动压反馈伺服阀的流量。动压反馈伺服阀将负载腔的扰动信号反馈到挡板组件，产生扰动力矩，并结合齿轮液压泵流量使滑阀阀芯位移变化，从而得到滑阀负载流量。液压缸的活塞根据滑阀负载流量拉伸或收缩，驱动作动圈旋转，从而实现IGV角度的精确控制。

2.1 IGV液压驱动部分建模

IGV系统驱动方式一般分为液压驱动和电机驱动。液压驱动较电机驱动具有输出力矩大、稳定性好等优点。因此，本文在后续的建模研究和仿真验证中采用液压驱动方式。

液压驱动部分结构如图3所示。该部分由齿轮液压泵、油箱、动压反馈伺服阀、液压缸组成。

图3 液压驱动部分结构图

2.1.1 齿轮液压泵模型

齿轮液压泵是一种容积式液压泵，由同尺寸且相互啮合的主动齿轮与从动齿轮组成。两个齿轮在容腔内无间隙啮合旋转，产生的差压将油液从吸油口吸入，使油液随着主动齿轮旋转充满容腔，并当两齿轮再次啮合时从排油口排出[6]。

齿轮泵由两个各项参数完全一致的齿轮相互外啮合组成，主动齿轮在时间t内以角速度ωg转过的角度φ为：

dφ=ωgdt

(1)

式中：φ为主动齿轮匀速转过的角度；ωg为主动齿轮转动的角速度，rad/s。

设主动齿轮的齿轮宽度为B，在时间t内主动齿轮扫过的体积Vw为：

(2)

式中：Vw为主动齿轮在时间t内扫过的体积，m3；B为主动齿轮的齿轮宽度，m；re1为主动齿轮节圆半径，m。

在时间t内从主动齿轮挤压出的液压油体积与齿轮节圆与啮合圆所形成空间的体积相同，即主动齿轮在时间t内排出的油液体积Vp1为：

(3)

式中：Vp1为主动齿轮在时间t内排出的油液体积；rc1为主动齿轮啮合圆半径，m。

由于从动齿轮和主动齿轮尺寸相同，从动齿轮宽度也为B，与主动齿轮转过相同的角度φ。从动齿轮在时间t内排出的油液体积Vp2为：

(4)

式中：rc2为主动齿轮啮合圆半径，m；re2为主动齿轮节圆半径，m。

因为两个齿轮的参数一致，则re1=re2=re、rc1=rc2=rc。在时间t内，齿轮液压泵排出的油液总体积Vp为：

dVp=dVp1+dVp2

(5)

根据排出的油液体积，可得齿轮液压泵瞬时流量q：

(6)

由此可见，在忽略温度、油液密度的情况下，齿轮液压泵的瞬时流量与齿轮的齿宽、节圆半径以及基圆半径等因素相关。当这些变量都不变时，齿轮泵的瞬时流量随着转过的角度呈抛物线规律变化。这和文献[7]的描述相符。

2.1.2 动压反馈伺服阀模型

动压反馈伺服阀在双喷嘴挡板伺服阀的基础上，增加了一个动压反馈回路，将滑阀负载扰动通过反馈喷嘴作用到挡板上。当系统处于动态工作状态下，动压反馈起反馈作用，增加了伺服系统的稳定性[8]。该模块由双喷嘴挡板阀、滑阀、动压反馈回路组成。

双喷嘴挡板阀是动压反馈伺服阀的先导级阀，由控制喷嘴、反馈喷嘴、衔铁挡板等组成。当衔铁挡板位于双喷嘴挡板阀中间时，输出的流量和压力差为零。对衔铁挡板进行受力分析可知，衔铁挡板受到控制喷嘴的液流力以及阀芯运动产生的负载力。

①左右两个控制喷嘴对衔铁挡板的液流力F为：

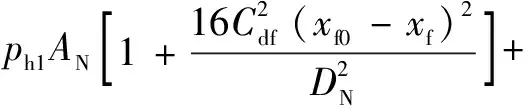
(7)

对左右两个控制喷嘴对衔铁挡板的液流力作差，可得控制喷嘴在挡板处产生的净液流力，为：

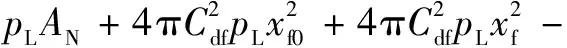
(8)

式中：pL为两控制喷嘴作用于挡板的压差，Pa,pL=ph1-ph2。

根据净液流力，可得控制喷嘴在衔铁挡板处产生的液压力矩TL1,为：

TL1=(F1-F2)r

(9)

式中：r为控制喷嘴中心至弹簧管中心的距离，m。

②喷嘴挡板阀阀芯的运动使反馈杆对衔铁挡板产生负载力矩TL2为：

TL2=Kf(r+b)[(r+b)ζ+xv]

(10)

式中：Kf为反馈杆刚度，N/m；r为控制喷嘴中心至弹簧管中心的距离，m；b为控制喷嘴中心到反馈杆小球中心的距离，m；ζ为衔铁挡板转角；xv为喷嘴挡板阀阀芯位移，m。

滑阀作为喷嘴挡板阀的负载，以节流原理工作，借助阀芯与阀套间相对运动对流量和压力进行控制。滑阀负载流量的方向和大小决定阀芯位移的方向和大小。则滑阀阀芯的流量平衡方程和阀芯受力平衡方程如下：

(11)

式中：Av为阀芯端面面积，m2；Cφ为滑阀的总泄漏系数；Pc为滑阀阀芯两端差压，Pa；Vta为进油腔和回油腔的总容积，m3；βe为油液的体积弹性模量，Pa；mv为滑阀阀芯质量，kg；Bv为滑阀阀芯粘性阻尼系数；Ks为稳态液动力刚度，N/m。

系统处于动态平衡时，动压反馈回路输入为负载压力扰动Pc，输出为反馈喷嘴作用于挡板的差压PL。由此，可建立动压反馈网络反馈活塞的动态平衡方程：

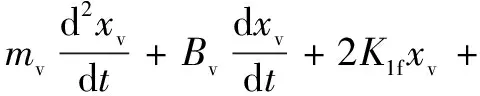
(pL1-pL2)An

(12)

式中：pc1为滑阀左腔压力，Pa；pc2为滑阀右腔压力，Pa；K1f为单个弹簧管刚度，N/m；pL1为控制喷嘴左腔压力，Pa；pL2为控制喷嘴右腔压力，Pa；An为滑阀活塞有效作用面积，m2。

2.1.3 液压缸模型

液压缸作为动压反馈伺服阀的负载，将液压能转化为机械能，是作直线往返运动的液压执行元件。假设：①动压反馈伺服阀和液压缸的连接管道对称，长度可忽略不计；②忽略管道中压力损失和动态损失；③液压缸的每个工作腔内各处压力相等[9]。取活塞的中间位置为初始位置，则流入液压缸进油腔的流量Q1和液压缸回油腔流出的流量Q2为：

(13)

式中：Ap为液压缸活塞的有效面积，m2；xp为活塞的位移，m；Vz1为液压缸进油腔的容积，m3；Vz2为液压缸回油腔的容积，m3；G1和G2分别为通往负载液压缸活塞两边的压力，Pa。

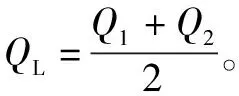
(14)

式中：GL为通往负载液压缸活塞两边的压力差，Pa；Vza为工作腔的总压缩容积，m3。

2.2 IGV机械传动部分建模

IGV系统机械传动部分由作动圈、支撑架、推杆、连杆机构、导叶等组成。作动圈通过弹簧装置架在支撑架上，克服了燃气轮机运行过程中支撑架热胀冷缩对作动圈的影响。在弹簧支架的顶部装有滚轮。滚轮与作动圈接触且相互之间可以运动。IGV机械部分采用双连杆结构，如图1所示，连杆1一端固定在作动圈上，连杆2一端固定在支撑架上。当IGV液压驱动部分推动推杆时，作动圈进行旋转，使连杆1跟随作动圈移动，并在连杆2的反作用力下旋转；连杆2在连杆1带动下使叶片转动，实现IGV系统角度控制。机械传动部分如图4所示。

图4 机械传动部分示意图

图4中：O为液压缸输出轴端点位置；Oi为铰接点1至铰接点4,i=1,2,…,4；x1为液压缸输出轴O沿x向位移；θj为机械臂j相对于机械臂(j-1)的相对摆角,j=2,3,4；θ5为IGV系统的输出角度，θ5=θ2+θ3+θ4。

忽略组件间摩擦力和转轴间隙，分别对每个铰接点进行动能、势能分析，建立以下IGV机械传动部分的运动方程：

(15)

式中：M为系统惯性矩阵；C为系统离心力和哥氏力项矩阵；G为系统重力矩阵；τ为广义力矩阵；θ为系统广义坐标，θ=[x1,θ2,θ3,θ4]T；T为每个铰接点的动能；U为每个铰接点的势能；Q为广义激振力矩阵。

以铰接点2为例，对其进行受力分析，得到动能T2、势能U2：

(16)

式中：I2为第2个机械臂对其质心的转动惯量，kg·m2；m2为第2个机械臂的质量，kg；v2为机械臂2质心的运动速度，m/s；d2为机械臂2的质心到铰接点2的距离，m。

将动能T2、势能U2代入拉格朗日方程，可得到铰接点2所受的广义力τ2与系统广义坐标θ的关系：

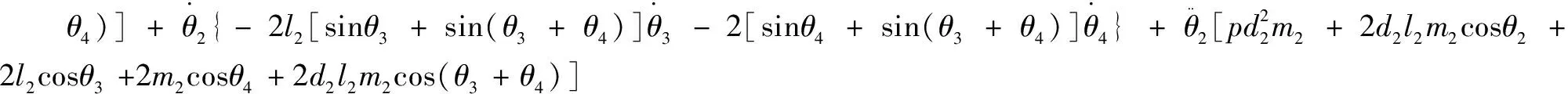
(17)

式中：l2为机械臂2的长度，m。

同理，对其他铰接点亦进行了类似分析。

通过Simulink分别建立液压驱动部分和机械传动部分的动力学模型，进而得到IGV系统模型。IGV系统模型如图5所示。

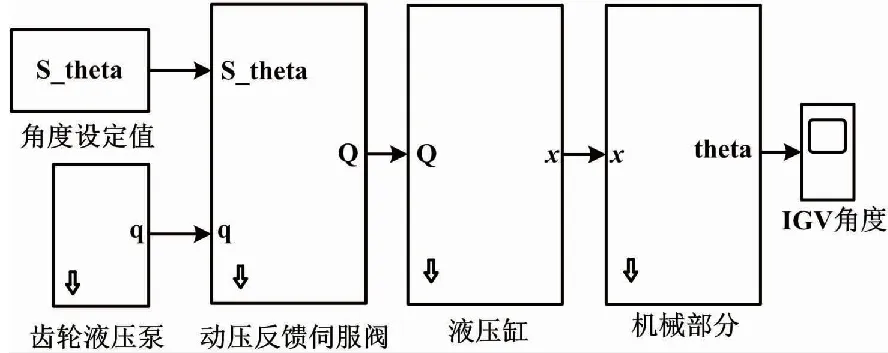
图5 IGV系统模型图

3 IGV系统典型故障建模

基于上述IGV系统仿真模型，本文对典型故障机理进行了分析，并建立了IGV系统故障模型。液压缸内部泄漏、叶片断裂和IGV连杆松动这三种故障在工业现场中发生概率高，对控制系统的安全、稳定运行影响较大[10]。因此，本节选取这三种典型故障进行建模研究。

3.1 液压缸内部泄漏

由于输送介质的冲刷磨损、腐蚀引起的密封性变异、安装误差、制造缺陷等问题，液压缸容易发生内部泄漏，可能导致系统响应时间变长、位置控制精度降低、燃气轮机机组运行效率下降，还可能导致压气机喘振，对机组的安全运行造成严重影响。液压缸内部泄漏故障模型如下：

(18)

式中：Ctp为液压缸总泄漏系数。

3.2 叶片断裂

IGV系统的叶片在长期运行过程中，负荷变化范围大，导叶动作频繁，容易产生疲劳裂纹。此外，空气潮湿导致叶片产生点状腐蚀，易导致叶片断裂。当叶片断裂后，导叶维持在原有角度，IGV系统停止运行[11]。通常用振动响应的大小来描述叶片断裂情况。叶片断裂故障下的叶片振动响应y为：

y(x,t)=E[H0+H′|cos(2πfrt)|]

(19)

式中：H0为稳定状态下的激振压力，Pa；H′为叶片断裂下的激振压力，Pa；fr为转子工频，Hz；t为时间，s；E为叶片弹性模量，GPa。

3.3 IGV连杆松动

随着IGV系统的长时间运行，连杆会出现轻微的倾斜，使驱动推杆与连杆形成切向扭矩；再加上机械部件老旧、导叶连接杆螺纹松动、部件间的磨损等原因，导致IGV连杆松动。

IGV连杆松动为渐变故障，破坏了液压驱动部分输出与IGV角度的对应关系，使IGV设定角度与液压缸的活塞行程发生偏差，即IGV角度设定信号继续增加而实际IGV开度无法增大到设定值。当IGV连杆松动故障发展到一定程度时，实际角度和指令角度的累积偏差超过机组的保护设定值，将引发机组跳闸。通常用磨损程度来描述IGV连杆松动情况，时间越长磨损越严重。本文基于Lewis提出的负荷磨损模型，建立IGV连杆松动故障模型[12]：

(20)

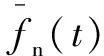
4 仿真结果与分析

为验证本文建立的IGV系统模型的准确性，本节分别对正常模型与故障模型进行了仿真与分析。

4.1 正常模型仿真与分析

本文使用所建模型模拟IGV系统在正常工况下导叶角度的变化，将其与燃机电厂2×100 MW联合蒸汽循环机组IGV角度的历史运行数据进行比较。正常工况下的电厂历史运行数据与模型输出数据对比如图6所示。

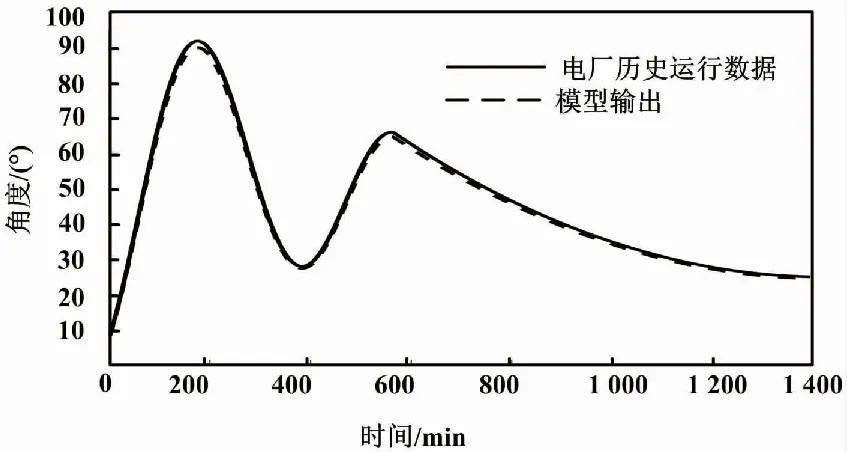
图6 正常工况下的电厂历史运行数据与模型输出数据对比

通过比较模型输出与电厂历史运行数据，可得到仿真数据与电厂历史数据的均方根误差为0.023。由此说明，IGV系统处于正常工况时，模型输出角度与电厂历史数据相吻合。这表明，所建模型能够准确地描述IGV系统的角度变化，验证了模型的准确性和有效性。

4.2 故障模型仿真与分析

各种故障下模型仿真曲线如图7所示。

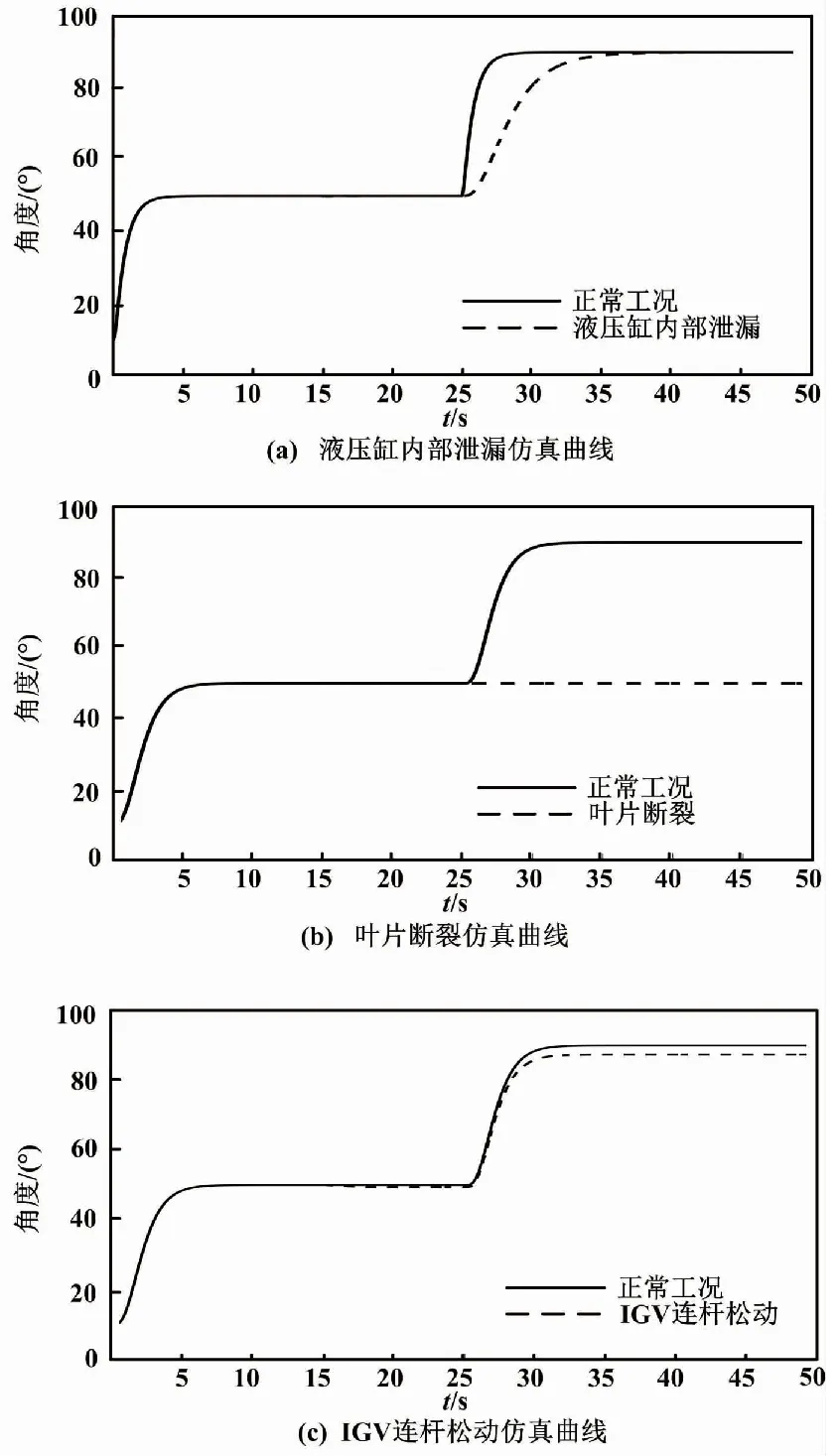
图7 各故障情况下模型仿真曲线

本文使用所建模型，模拟IGV系统在典型故障情况下导叶角度的变化，设定如下：输入信号为阶跃信号；IGV初始角度设定值为0；故障发生在第15 s；前25 s IGV角度设定为50°；25 s时IGV角度设定为100°。由于IGV连杆松动为渐变故障，在实际控制系统中，渐变故障发生所需时间较长。为便于仿真研究，本文假设式(18)中的摩损切向平均载荷高于正常工况下的载荷，使得IGV连杆松动故障在较短时间内发生。

由图7(a)可知，当液压缸内部泄漏故障发生时：15～25 s内故障特征并不明显，对液压缸进油量和回油量影响较小，输出导叶角度维持不变；在25 s时，增大IGV角度设定值，输出的导叶角度仍能增加至设定值，但液压缸内油压下降导致系统响应时间过长，机组运行效率下降。由图7(b)可知：在叶片断裂故障发生前，输出的导叶角度能够跟随设定值；15 s时故障发生后，IGV系统不再运行，导叶维持原有角度不再变化。由图7(c)可知：当IGV连杆松动故障发生时，模型中导叶角度迅速下降，与正常工况下IGV角度偏差超过3%；在25 s时增大IGV角度设定值后，输出的导叶角度仍能跟随设定值，但由于连杆松动导致作动圈与连杆之间受力失衡，其与设定角度存在固定偏差。

综上可知，各典型故障情况下的模型输出均与故障机理的分析结果相符，仿真曲线与故障机理分析高度一致，说明本文所建IGV系统故障模型具有较高的准确性。

5 结论

本文以重型燃气轮机双连杆型IGV系统为研究对象，对其进行了建模与故障仿真研究。通过对IGV系统的结构和机理进行分析，建立了IGV系统液压驱动部分与机械传动部分仿真模型，并与燃机电厂IGV历史运行数据进行对比。本文所建IGV系统模型能准确反映IGV角度的变化，误差较小。通过分析IGV系统的故障机理，建立了液压缸内部泄漏、叶片断裂和IGV连杆松动这三种典型故障模型，并与正常工况下的模型进行对比。对比结果表明，IGV系统故障模型与故障机理分析结果基本符合，具有较高准确性。本文所建IGV系统建模与故障仿真具有良好的研究前景，为燃气轮机IGV系统的动态分析和故障诊断提供了重要的技术参考。