基于数据驱动的控制器综合性能优化

王志国，陈军军，刘 飞

(江南大学物联网工程学院，江苏 无锡 214122)

0 引言

在石油、化工及轻工等工业过程中，运行着众多类型的控制回路，其性能优劣直接影响整个控制系统的精度。这些回路的控制参数一般都会在系统投入初期被仔细地调节。但随着时间推移，构成控制系统的各个环节本身、操作环境以及工作点等可能会发生变化。这就需要对控制性能进行实时监控，并在性能不良时校正控制器。近年来，数据驱动控制器校正和设计方法因其无需系统辨识过程而引起广泛关注[1]。

基于数据驱动的控制器校正方法是一种无模型方法，可以利用系统工作数据对控制器参数直接调节。1994年，Hjalmarsson等[2]提出了迭代反馈校正方法(iterative feedback tuning，IFT)，利用多次闭环试验数据并基于梯度迭代实现控制器参数整定。随后，Campi等[3]引入虚拟参考信号，通过系统输入端的实际数据与虚拟输入数据辨识控制器参数，也就是虚拟参考反馈校正(virtual reference feedback tuning，VRFT)方法。该方法为 “一次性”数据驱动方法，避免了IFT因多次试验造成的成本和时间浪费。2018年，Boeira等[4]将VRFT拓展到多输入/多输出系统中，实现了多变量控制器参数的无偏估计，并将其与预测控制进行了性能对比。另外，针对频繁负载扰动问题，Eckhard等[5]通过引入虚拟扰动信号，改善了VRFT方法在扰动环境下的适应能力。2019年，Ikezaki等[6]通过虚拟一个内部模型结构，利用闭环输出数据直接辨识控制器参数，提出了虚拟内模调整方法(virtual internal model tuning，VIMT)。该方法只需一组闭环输出数据即可实现，并且规避了VRFT求解期望传递函数的逆和输入功率谱的过程。

在上述数据驱动的控制器校正方法中，参考模型的选择会直接影响实际控制系统的性能。文献[1]提出以二阶系统加延迟环节作为参考模型的基本形式，但对具体的上升时间与阻尼系数如何选择没有深入解释。文献[6]通过对损失函数频域特性以及灵敏度函数的分析，指出参考模型的响应速度快于初始响应速度可提高校正后控制器的性能。文献[7]提出一种选取参考模型的指导原则，即参考模型需要包含系统非最小相位零点，并且其相对度不能小于被控对象的相对度(因果关系)。但是该方法的具体实施过程比较复杂，且所选取的参考模型无法保证控制系统的性能为最优。

与此同时，控制性能评估(control performance assessment，CPA)技术提供了多种不同的、用于评价控制器性能的指标。其中，基于最小方差(minimum variance，MV)基准的指标为一种随机性能指标，描述控制器对随机扰动的抑制能力[8]。而绝对误差积分(integral absolute error，IAE)为一种确定性能指标，用来描述控制器的跟踪能力以及抗扰动能力[9]。为使所设计的控制器获得最佳的控制性能，本文通过融合IAE与MV基准构造新的综合性能指标，提出一种数据驱动的控制器校正方法。主要创新工作包括：①通过分析VRFT与内模控制(internal model control，IMC)之间的联系，提出一种VRFT参考模型的结构选择方法；②构造一种综合性能指标，并基于该指标确定参考模型中的滤波器参数；③从实现方式和控制性能两个方面，将所提方法与传统比例积分微分(proportional integral differential,PID)控制器以及IMC-PID控制结果进行对比，验证了其优越性。

1 数据驱动的控制器校正原理

一般而言，基于数据驱动的控制器设计所参考的控制系统如图1所示。

图1 控制系统示意图

图1中：r(t)为输入的参考信号；P(q-1)为模型未知的被控对象；y(t)为输出信号；u(t)为控制信号，这里也是被控对象的输入信号；Tdes(q-1)为参考模型；ydes(t)为期望的输出信号；C(ρ,q-1)为控制器，具有以下一般性结构。

(1)

式中：ρ为可调控制参数ρi组成的向量;q-1为后移算子。

常用的PID控制器可看作式(1)的特殊形式。对于式(2)所示结构PID控制器，令式(3)成立，则包含有控制器参数ρ1、ρ2、ρ3的一般结构控制器表达式如式(5)所示。

(2)

式中：Δ=1-q-1为差分算子;kp为比例增益;Ti为积分时间常数;Td为微分时间常数;Ts表示采样时间。

令：

(3)

(4)

图1中，系统闭环输出与期望输出分别表示为：

(5)

式中：T(q-1)为实际系统的闭环传递函数。

T(q-1)的形式为：

(6)

基于数据驱动的控制器设计目标是实际输出信号完全跟踪期望信号。因此，定义损失函数为：

(7)

最小化J(ρ)即可获得最优控制器参数ρ*。

(8)

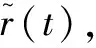
(9)

(10)

(11)

文献[3]已经指出，在引入合适的滤波器L(q-1)对观测输入、输出数据进行滤波后，以J1(ρ)为损失函数的优化问题可无限接近以J(ρ)为损失函数的优化问题。最佳滤波器L(q-1)形式为：

L(q-1)=Tdes(q-1)[1-Tdes(q-1)]

(12)

此时，滤波后的观测数据表示为{uL(t),yL(t)}，且有：

(13)

结合式(9),可得滤波后的系统虚拟误差信号和虚拟输入信号，为：

(14)

此时，损失函数J1(ρ)重新整理为：

(15)

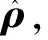
(16)

其中：

φL(t)=β(q-1)[Tdes-1(q-1)-1]y(t)L(q-1)

2 参考模型的结构选择

VRFT方法中，参考模型Tdes(q-1)的选择直接影响实际控制系统的性能。IMC作为史密斯预估控制的拓展，具有很好的鲁棒性和跟踪性能。理想内模控制器作用下的闭环传递函数形式符合文献[7]提出的选取VRFT参考模型的指导原则。因此，可以通过建立VRFT与IMC之间的联系，给出VRFT参考模型的基本形式。

根据VRFT的设计过程，考虑损失函数J1=0的理想情况。此时，控制系统的实际输出完全跟随期望输出，对应的闭环传递函数与参考模型相等，即T(q-1)=Tdes(q-1)。根据式(6)，可得最优控制器C*(ρ,q-1)为：

(17)

(18)

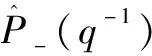
由IMC设计原则[9]，可得内模控制器CIMC(ρ,q-1)为：

(19)

式中：F(q-1)为一阶滤波器，

(20)

式中：ε为滤波器参数;Z[·]为Z变换;F(s)为复频域中一阶滤波器(文中所有涉及复变量s的表达式都是指在复频域中表现形式，可以通过反拉氏变换、Z变换转为时域或频域的表现形式)。

通过对IMC的分析可知，内模控制器CIMC(ρ,q-1)与一般反馈控制器C(ρ,q-1)的关系如下：

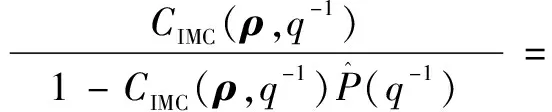
(21)

(22)

根据IMC原则设计的最优反馈控制器形式为：

(23)

比较式(17)与式(23)可知，如果取式(24),即当理想内模控制器作用下的期望闭环传递函数TIMC-des(q-1)与VRFT中所选择的参考模型相同时，由IMC原则所设计的反馈控制器和VRFT方法所得最优控制器一致。

(24)

因此，可将理想内模控制器作用下的期望闭环传递函数作为VRFT的参考模型的基本形式。

考虑被控对象为稳定线性时不变过程，且没有积分环节和负零点，则可用一阶时滞(first order plus pure dead time，FOPDT)模型或二阶时滞(second order plus pure dead time，SOPDT)模型对其近似：

(25)

(26)

式中：K为被控对象的增益;T1、T2为时间常数;θ为延迟时间。

这样，只需确定式(24)中的滤波器参数ε与延迟时间θ，便可得到最终的参考模型。

3 基于综合性能指标确定参考模型

基于性能指标的控制器设计可使控制器性能根据用户的期望指定。IAE指标和MV指标分别用于评价控制器对设定值的跟踪能力和对随机扰动的抑制能力。以其中某一个指标为基准设计的参考模型，在该指标下具有对应的控制性能最优性。

3.1 IAE指标下的最优参考模型

根据IMC-PID的设计规则，过程模型为FOPDT时，设计所得的内模控制器对应的PID控制器参数为：

(27)

同样地，SOPDF模型对应的控制器参数为：

(28)

此时，图1所示闭环控制系统中设定值到输出端的闭环传递函数T(s)为：

(29)

将分母的延迟环节进行泰勒近似，即e-θs≈1-θs，可得：

(30)

则系统单位阶跃下的输出响应为：

(31)

拉氏反变换后可得时域下的输出y(t),为：

(32)

误差信号e(t)为：

(33)

此时，控制系统取得最优的IAE性能指标I[10]，为：

(34)

为减小使用泰勒近似延迟环节所导致的IAE估计误差，可通过Pade来近似延迟环节e-θs。其对应的最优IAE性能指标为：

(35)

如已知或估计得到延迟系数θ，则由式(35)可确定最优滤波器参数ε*。相应的最优IAE性能指标下的参考模型表达式为：

(36)

3.2 MV指标下的最优参考模型

MV指标是以控制系统在最小方差控制器作用下的理论最小输出方差为基准，定义的一种随机性能指标，用于评价控制系统对随机扰动的抑制能力。考虑单回路线性控制系统，假设存在高斯白噪声ξ(t)经扰动模型N(q-1)后叠加于系统输出端。在不影响随机控制性能分析的前提下，假设输入设定值为零，则系统的闭环输出为：

y(t)=P(q-1)u(t)+N(q-1)ξ(t)

(37)

输出信号可表示为：

(38)

在最小方差控制器作用下，式(38)中的输出信号y(t)可取得最小方差。以此为基准，定义基于MV的控制性能评价指标η，为：

(39)

η值可直接利用控制系统闭环输入输出估计获得[8]。η的取值范围为0～1。该值越接近1,表示控制性能越好；反之，则表示控制性能差。

(40)

式中：Ts为采样时间。

此时,控制系统的输出和滤波器参数ε有关。在已知系统延迟系数θ的前提下，调整ε可使控制系统输出方差向理论最小方差靠近。从基于MV的控制性能指标η上评价，使η达到最大时可以得到最优的滤波器参数ε*。由此可得到MV指标下的最优参考模型,为：

(41)

3.3 基于综合性能指标的参考模型

根据3.2节分析可知，由IAE指标确定参考模型时所设计的控制系统具有良好的阻尼性和瞬态响应特性，且超调量小。而根据MV基准选定的参考模型对应的控制系统输出方差小，但鲁棒性较差，且控制器信号波动大。结合上述两种方法各自的特点，定义以下综合性能指标。

(42)

式中：Iopti为随ε取值变化的IAE下限值；ηi为随ε取值变化的MV控制性能指标值；λ为权重系数，0≤λ≤1。

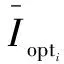
(43)

求解式(43)的最优化问题,即可得到综合性能指标下的滤波器参数ε*，从而确定参考模型：

(44)

这里需要说明的是，综合性能指标下获得的VRFT方法参考模型结构是根据VRFT与IMC的关联性选择的。因此，理想情况下VRFT校正的控制器可以取得与内模控制相同的控制效果。但作为数据驱动方法的VRFT不需要对被控对象进行模型辨识。同时，VRFT也减少了内模控制设计过程中由于延迟环节近似处理产生的误差。因此，采用改进的VRFT方法进行控制器校正后的控制性能相对更好。

4 数据驱动的控制器性能优化算法步骤

本文所提的以综合性能指标为设计基准、基于数据驱动方法的控制器校正算法实现步骤如下。

①采集在运行控制系统的闭环输入输出数据{u(t),y(t)},t=1,2,...,N。

②系统延迟时间θ已知或对其进行估计。

③使用闭环数据估计式(39)的控制性能指标η。如控制性能满足设计要求，则跳转到步骤⑩；反之，运行步骤④。

④分别根据式(35)和式(40)，计算滤波器参数ε和性能指标Iopt的关系曲线，以及滤波器参数ε和性能指标η的关系曲线。

⑤选取权重系数λ，然后根据式(43)得到滤波器参数ε和综合性能指标的关系。

⑥根据式(44)，以最优综合性能指标对应的滤波器参数ε*确定参考模型Tdes(q-1)。

⑦根据式(12)确定L(q-1)。

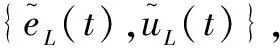
⑨更新PID控制器参数，然后跳转到步骤①。

⑩结束。

5 仿真研究

为验证所提方法的有效性和优越性，分别通过一个数值仿真和一个实际的发酵过程温度控制系统对其进行测试。

5.1 数值仿真

考虑一个有时滞的单回路反馈控制系统，被控对象P(s)为：

(45)

均值为零、方差为0.012的随机扰动信号ξ(t)经过干扰模型N(q-1)叠加于系统的输出端。

(46)

控制器为PID形式，其初始参数为kp=0.3、Ti=4、Td=0。

图2为仿真所得系统输出响应曲线。

图2 系统输出响应曲线(仿真)

由图2可知，在初始PID控制作用下，系统的动态响应存在较大波动，其最大超调量达到69.8%。采集系统闭环输入输出数据，估计可得当前系统基于MV的控制性能指标η=0.489 7，实际IAE指标值为I=33.98。结合式(34)，可以得到Skogestad[9]方法下(即ε=θ)系统的IAE下限为20，远小于当前系统的实际指标IAE值。由此反映出此时系统的累积误差大，设定值的跟踪能力弱，控制性能差。

使用本文方法对上述系统进行控制器参数校正。取权重系数λ=0.5，根据第4节的校正算法，计算可得如图3所示的综合性能指标随滤波器参数的变化曲线。

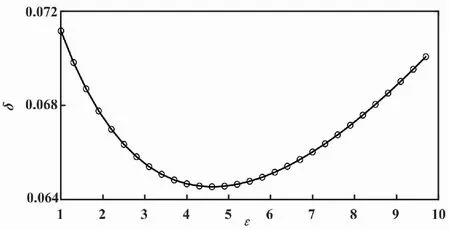
图3 综合性能指标随滤波器参数变化曲线(仿真)

选取综合性能指标最小值对应的滤波器参数ε=4.7。则VRFT算法所用参考模型可确定为：

(47)

根据第4节步骤⑧，估计可得校正后的控制器参数为kp=0.245 1、Ti=6.754 3、Td=1.157 3。

由图2可知，校正后控制系统的输出响应改善明显，动态响应速度快，且无超调量。此时系统的实际IAE值为13.78、基于MV的控制性能指标η=0.745 2。与初始情况相比，校正后的控制系统性能得到大幅提升。

图4为由IMC-PID方法设计的控制器和本文方法所得控制器分别作用下的系统闭环输出响应。

图4 IMC-PID与所提控制方法的输出响应曲线(仿真)

由图4可知，由IMC-PID方法设计的控制器对应的系统闭环输出超调小。此时，系统的实际IAE值为16.90，MV性能指标η=0.683 5，而本文方法的上升时间与调节时间比IMC-PID更快、IAE值更低、MV指标也更趋近于1。由此说明，本文方法具有更好的响应速度以及跟踪性能。产生这一区别的原因，正如3.3节所述，IMC-PID设计控制器过程中需要对延迟环节进行Taylor或Pade近似时存在误差所致。

5.2 工业实例

本节以某工厂啤酒发酵过程温度控制回路为工业实例进行分析。

发酵罐内部温度由流经罐体夹套的冷媒流量控制。建模所得发酵液温度T与冷媒流速Qv之间的关系可以近似为[12]：

(48)

温度控制回路为单回路PID控制结构。初始PID参数为kp=0.2、Ti=17.857、Td=36.1。

发酵过程温度控制流程如图5所示。

图5 发酵过程温度控制流程图

图6为该实例的系统输出响应曲线。

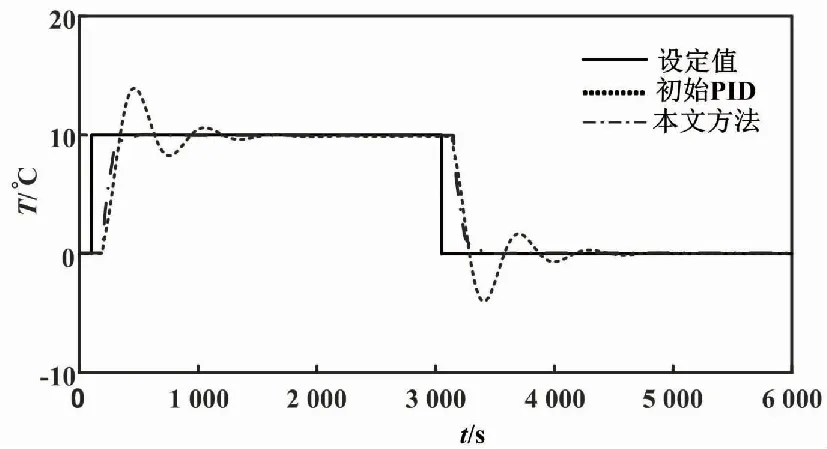
图6 系统输出响应曲线(实例)

由图6可知，初始PID控制作用下，系统的动态响应存在较大波动，其最大超调量达到41.3%，调节时间为1 386 s。采集控制系统闭环输入输出数据，估计可得当前系统基于MV的控制性能指标η=0.497 4，实际IAE指标值为2 927。作为参照的Skogestad[9]方法下，系统的IAE下限为1 740，远小于当前系统的实际IAE指标值。由此，反映出此时系统的累积误差大，设定值的跟踪能力弱，控制性能差。

根据控制系统闭环输入输出数据，使用本文方法对上述系统进行控制器参数校正。取权重系数λ=0.9，可得综合性能指标随滤波器参数变化的关系如图7所示。

选取综合性能指标取得最小值对应的滤波器参数ε=53，则VRFT算法所用参考模型可确定为：

(49)

利用本文所提方法校正后的控制器参数为kp=0.658 6、Ti=73.916 9、Td=25.919 3。

由图7可知，校正后控制系统的输出响应改善明显，动态响应速度快，且无超调量。此时系统的调节时间为315 s，实际IAE指标值为1 412，基于MV的控制性能指标η=0.763 4。与初始情况相比，校正后的控制系统性能得到大幅提升。

图7 综合性能指标随滤波器参数变化的示意图(实例)

进一步将本文方法和IMC-PID方法所设计的控制器进行比较。根据IMC-PID规则所设计的PID控制器参数为kp=0.433 1、Ti=63.4、Td=10.354 9。

图8为IMC-PID与本文方法控制的输出响应曲线。

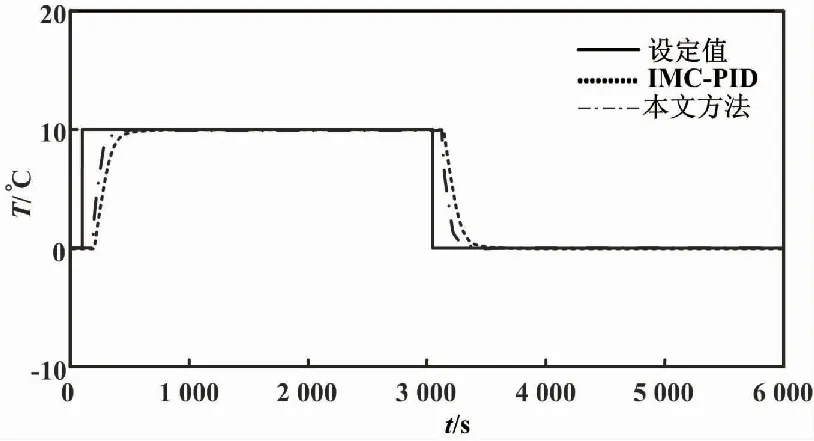
图8 IMC-PID与本文方法控制的输出响应曲线(实例)

由图8可知，由IMC-PID方法设计的控制器对应的系统闭环输出无超调，调节时间为430 s，系统的响应速度比本文所提方法更慢。另外，表1给出了控制器调整前后的性能。

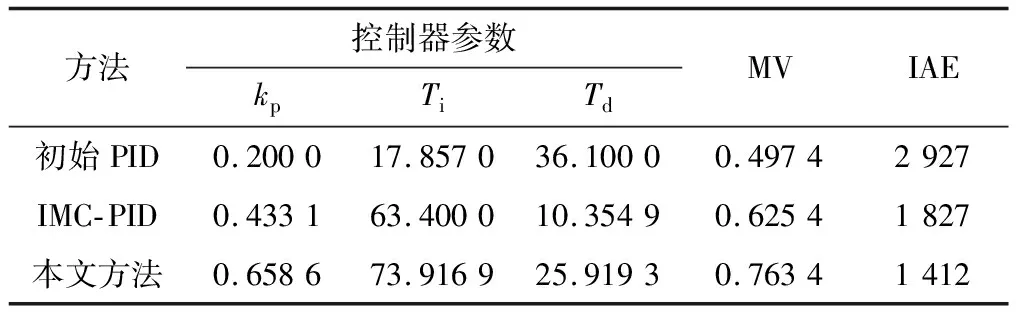
表1 控制器调整前后的性能

由表1可以发现，根据本文方法校正后的控制系统实际的IAE值为1 412，低于IMC-PID控制与初始PID控制下的IAE指标值;而MV性能指标η=0.763 4，也更接近于1，说明本文方法校正后的系统设定值跟踪能力更好，对扰动的抑制能力更强，具有更好的随机性能和确定性能。

6 结论

本文将控制性能评估技术与数据驱动控制方法相结合，提出一种数据驱动的控制器综合性能优化方法。研究结果表明，在所定义综合性能指标下选定的VRFT参考模型，其数据驱动的控制器校正效果相比一般经验法确定的PID控制性能改善明显。同时，本文也将所提方法和基于IMC-PID规则设计的控制器进行了对比。本文方法不仅减少了IMC-PID设计过程中由于延迟环节近似处理产生的误差，而且作为一种基于数据驱动的方法，整个算法可利用闭环控制系统输入输出数据实现，无需已知过程模型信息或系统辨识。本文定义的综合性能指标是对IAE指标和MV指标进行权重组合，而根据指定控制性能设计出可使控制系统在确定性能和随机性能同时最优的新指标还需进一步研究。另外，后续还需考虑所定义性能指标能包含对控制信号的约束处理，以降低控制器输出波动。