城市隧道半敞开段结构受力分析

邹涛

（上海市政交通设计研究院有限公司，上海市 200030）

0 引言

城市道路明挖隧道暗埋段一般采用箱形框架结构，在道路中央分隔带较宽的情况下，设置一定长度的半敞开段，能显著改善隧道内的通风、照明及视觉效果，提高行车的安全性和舒适性，达到节能运营的目的。但是顶板开洞使隧道结构的受力变得复杂，设计中广泛采用的二维平面框架模型无法真实反应隧道结构的内力状况，对于隧道顶板开洞部位，计算结果存在较大偏差，导致截面尺寸和配筋不合理[1]。三维空间板壳计算模型的合理性和精细化程度更高，能考虑顶板开洞对隧道主体结构内力的影响，使结构内力结果更加符合真实情况[2]。

现结合郑州市某城市隧道工程，建立隧道半敞开段的三维空间模型，对顶板是否开洞，以及开洞后不同横梁布置方案的内力计算结果进行分析比较，探讨隧道半敞开段结构受力特性。

1 工程实例

该隧道规模为双向六车道，暗埋段采用两跨箱形框架结构，结构宽度27.4m，单孔结构净尺寸12.3m×5.6m。隧道暗埋段中有200m为半敞开段，顶板开洞尺寸为5m，顶板厚1.1m，底板厚1.1m，侧壁厚1.0m，中隔墙厚0.8m，顶部挡墙厚0.5m，结构以30m为一个节段，结构横断面见图1所示。

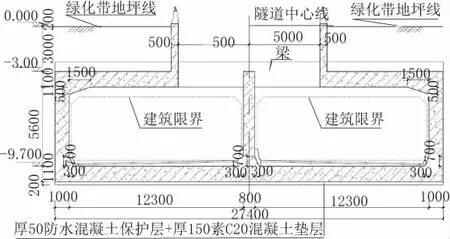
图1 隧道镂空段结构横断面图（单位：mm）

隧道混凝土强度等级为C35，顶板覆土厚度为3m，土层天然重度取18kN/m3，侧向土压力系数为0.5，地下水位埋深为2.2m，底板下垂直基床系数为17MPa/m，荷载考虑结构自重、覆土荷载、侧向水土压力、地面超载及其引起的侧向压力、水浮力。现主要讨论隧道结构正常使用极限状态（浮力工况）下的内力，标准组合下的荷载如表1所列。

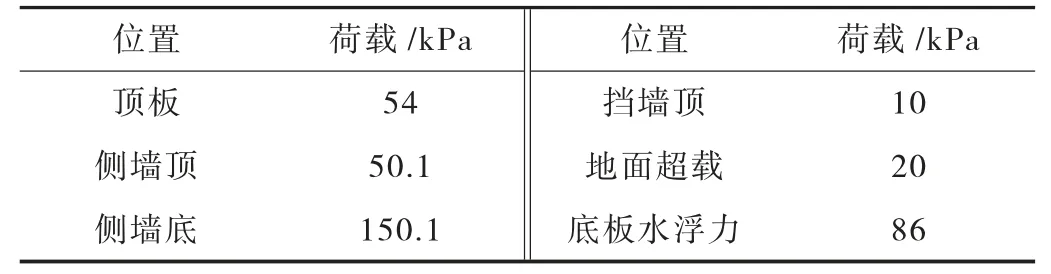
表1 隧道荷载计算表

2 计算模型

由于顶板开洞较大且贯穿整个节段，为保证开洞后顶板的横向刚度，予以增设横梁，以增加结构的稳定性，使侧壁不产生过大的水平变形。

杆件的线刚度定义为：

式中：E为材料弹性模量；I为杆件截面惯性矩，对于矩形梁I=bh3/12（b、h为梁宽、梁高），对于纵向每米板I=t3/12（t为板厚）；l为杆件长度。

开孔段横梁截面为矩形，线刚度为i1；梁板叠合段横梁截面等效为倒T形（翼缘宽度为梁纵向中心间距），线刚度为i2；则横梁等效线刚度为i=i1i2/（i1+i2），横梁纵向每米等效线刚度为i/d，d为横梁纵向中心间距。开洞前纵向每米顶板的线刚度i为2.65×105kN·m/m，横梁截面尺寸及间距根据开洞前纵向每米顶板的线刚度来选择，横梁纵向每米等效线刚度取值约开洞前顶板的1.5倍，详见表2所列；为预留管线敷设空间，梁顶覆土不小于2m，同时为保证通风效果，增设横梁后需保证一定的开孔率，据此提出以下三种方案（见表2）。

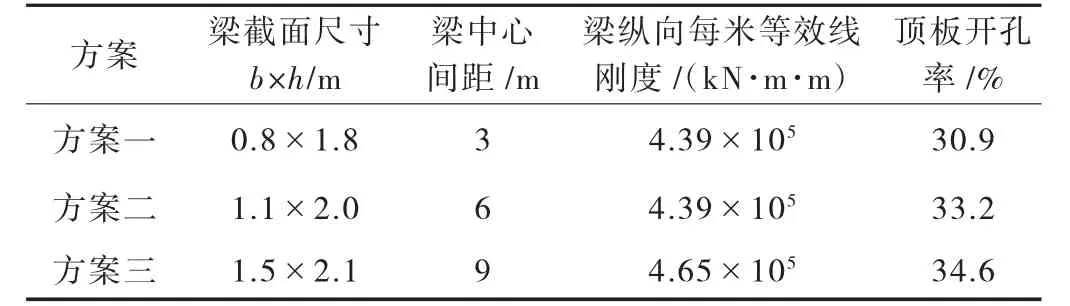
表2 横梁布置方案表

结构顶板、底板、侧壁及顶部挡墙均采用板壳单元模拟，梁、柱采用梁单元模拟，底板采用曲面弹簧模拟地基反力。计算采用软件AutodeskRobot StructuralAnalysis，方案一计算模型见图2所示，方案二、三模型除横梁截面及间距不同，其余均同方案一。为了与未开洞前进行比较，还建立了未开洞情况下的三维有限元模型（未列出）。为便于结果分析，计算中板单元X轴平行于隧道横断面方向，Y轴平行于隧道纵轴线方向，因而，任一点的MX为该点的横断面弯矩，MY为纵轴向弯矩。梁、板弯矩方向均以三维模型外侧受拉为负，内侧受拉为正。

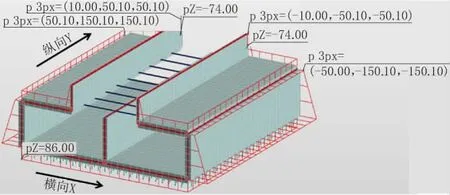
图2 方案一结构有限元模型

3 计算结果与分析

3.1 计算结果

通过有限元计算，考察三种方案的结构受力情况。分别提取模型中板弯矩计算结果，可以得出三种方案底板、侧壁弯矩分布规律一致，下面以方案一进行说明。

图3、图4为方案一MX、MY分布云图。可以看出，底板、侧壁MX沿纵向均匀分布，MX约为MY的5倍，呈现出横向框架的受力特征；底板在靠近侧壁和中隔墙处板底受拉，出现最大负弯矩，在跨中处板顶受拉，出现最大正弯矩；侧壁均为板外侧受拉，最大负弯矩出现在靠近底板处；未开洞模型底板、侧壁也展现了上述弯矩分布规律，因此顶板开洞未影响底板、侧壁弯矩分布。顶板受开洞及横梁间距影响，MX、MY分布规律接近于双向板。

图3 方案一MX分布云图（单位:kN·m）

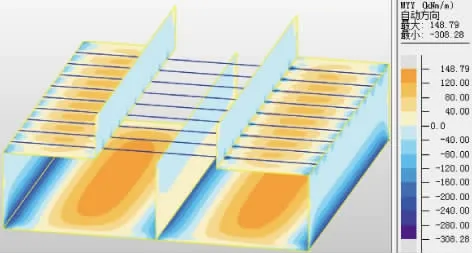
图4 方案一MY分布云图（单位:kN·m）

3.2 计算结果分析

表3列出了三种方案的底板MX、MY值，可以看出，三种方案弯矩值接近。跨中MX随横梁间距的增大而减小；由于顶板开洞，结构顶板覆土荷载减小，造成顶板对侧壁、顶板的约束能力减弱，底板MX、MY均较开洞前减小，跨中弯矩值减小约23%，支座弯矩值减小约34%。

表3 不同方案底板MX、MY比较表

由于结构沿Y向对称，选取右侧一半顶板进行分析，图5为三种方案顶板MX分布云图。可以看出，顶板仅在侧壁、洞边处出现负弯矩，最大负弯矩均出现在侧壁处，侧壁处弯矩值约为洞边处的1.5倍；随着横梁间距减小，MX沿纵向逐步趋于均匀分布。

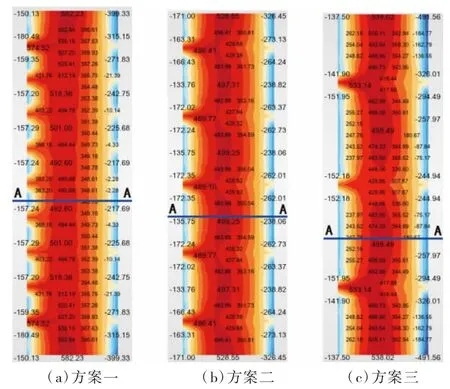
图5 顶板MX分布云图（单位:kN·m）

提取靠近结构X向对称轴的一跨顶板中心线A-A剖面处的MX值（见图6）。可以看出，三种方案MX大小及分布规律基本一致，横梁间距对MX影响很小。顶板开洞后MX较开洞前均减小，侧壁处减小约65%，跨中减小约50%；由于开洞使板在洞边处的约束减弱，分担弯矩减小，最大正弯矩及弯矩反弯点位置均向侧壁方向移动。

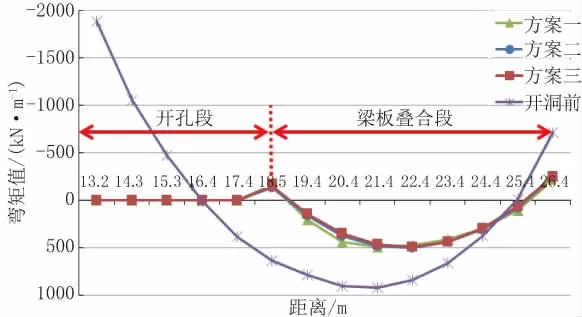
图6不同方案顶板MX对比图（单位:kN·m）

图7 为三种方案顶板MY分布云图。可以看出，顶板仅在横梁与洞边相交处、侧壁处出现负弯矩，方案三在横梁附近也出现负弯矩。在横梁与洞边相交处出现明显的应力集中，最大负弯矩也出现在该处，弯矩值约为侧壁处的3倍，且随着横梁刚度、间距的增大而增大。因此，顶板配筋时需对横梁与洞边相交处顶部纵向钢筋适当加密。

图7 顶板MY分布云图（单位:kN·m）

图8为顶板Y向中心线B-B剖面处的MY值。可以看出，开洞前顶板纵向均为板底受拉，开洞后最大正弯矩较开洞前均减小，方案一减小约40%，方案二、方案三减小约28%。方案一顶板纵向未出现负弯矩，均为板底受拉，方案二、方案三在横梁处出现负弯矩；三种方案最大正弯矩数值接近，分别为100.6kN·m、134.5kN·m、122.9kN·m。因此，横梁间距对MY分布影响较大，但对MY最大正弯矩值影响较小，随着横梁间距增大，出现板顶受拉的情况。

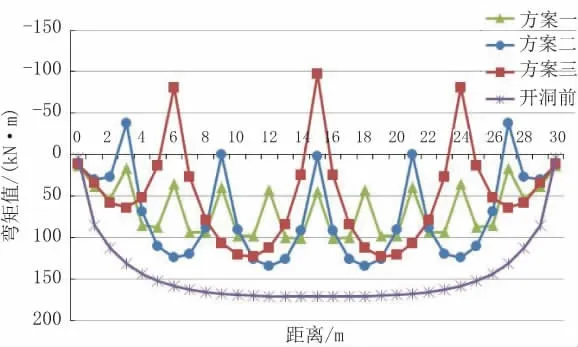
图8不同方案顶板MY对比图（单位:kN·m）

图9 为三种方案模型X向对称轴处横梁轴力对比图。可以看出，在梁板叠合段轴力从侧壁向洞边逐步增加，在洞边处急剧增长；轴力最大值出现在开孔段，且保持不变；不同方案轴力最大值随横梁间距的增大呈线性增加；梁板叠合段在计算梁内力时考虑了顶板作为横梁翼缘的协同作用，方案一横梁与顶板刚度比最小，梁轴力增长最缓慢，因此计算结果是符合实际的。

图9 不同方案横梁轴力对比图（单位：kN）

提取模型X向对称轴处横梁弯矩计算结果，可以得出三种方案横梁弯矩分布规律一致。下面以方案一进行说明（见图10）：开孔段弯矩呈线性变化，并在中隔墙处出现最大负弯矩，洞边处出现最大正弯矩，反弯点距洞边约1.5m；梁板叠合段仅在侧壁附近出现负弯矩，且弯矩值远小于中隔墙处。

图10 方案一横梁弯矩图（单位:kN·m）

表4列出了三种方案的横梁不同位置弯矩值，可以看出，三种方案侧壁处弯矩值接近，中隔墙处弯矩值约为洞边处的2.6倍，洞边、中隔墙处弯矩值随横梁间距的增大呈线性增加。

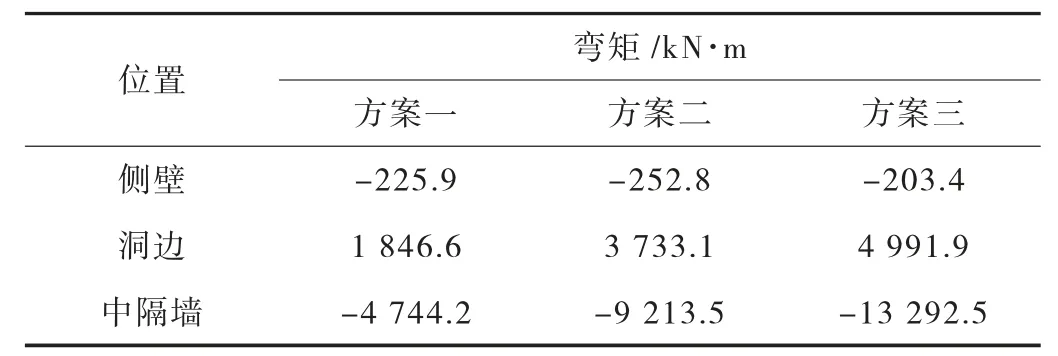
表4 不同方案横梁弯矩值比较表

根据GB50010—2010《混凝土结构设计规范》（2015年版）进行梁纵向受力筋的配筋计算，裂缝控制等级为三级[3]，配筋结果见表5所列。可以看出，方案二、三横梁在中隔墙处梁顶部钢筋直径大、数量多，需要分4层配置，混凝土的浇筑质量难以保证。

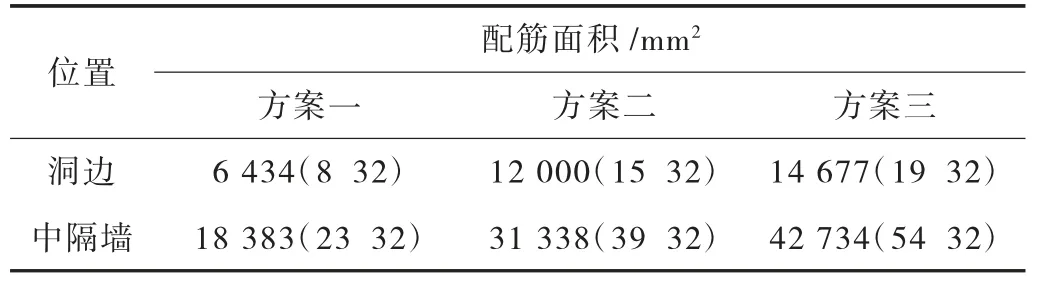
表5 不同方案横梁纵向配筋结果比较表

经过上述分析，三种方案顶板开洞率接近，为减小顶板横梁与洞边相交处纵向应力集中，充分发挥梁板的协同作用，减小横梁中隔墙处梁顶部钢筋数量，施工图设计中采用方案一。横梁剪力最大值出现在中隔墙处，为了缓解横梁下中隔墙局部应力集中现象，增大结构的整体刚度，使结构内力趋于合理分布，在侧壁、中隔墙横梁下位置设置暗柱[4]。

4 结语

通过建立三维有限元模型对隧道半敞开段顶板是否开洞，以及开洞后不同横梁布置方案的内力计算结果进行分析比较，主要结论如下：

（1）顶板开洞未影响隧道底板、侧壁的内力分布规律，但横、纵向弯矩值较开洞前减小，且顶板横梁间距对弯矩值影响较小。

（2）开洞后顶板内力分布接近于双向板，横、纵向弯矩值较开洞前减小。顶板横向弯矩受横梁间距影响较小，分布规律与开洞前基本一致。随着横梁间距减小，沿纵向逐步趋于均匀分布；顶板纵向弯矩分布受横梁刚度、间距影响较大，随着横梁刚度、间距增大，顶板纵向出现板顶受拉的情况。

（3）顶板横梁轴力、弯矩值随横梁间距的增加呈线性增加。施工图设计中采用横梁刚度、间距较小的方案一，横梁与顶板刚度比最小，梁板的协同作用最明显，结构内力分布更合理。

本文计算分析仅是对一个隧道半敞开段实例结构内力分布的探索，实际工程中隧道跨度、高度、开洞尺寸、埋深、周围土体参数等均不同，研究隧道半敞开段的内力分布规律，需对以上各因素进行详细对比分析。